schade (peinlich?), dass ich das nicht wusste

(Wachstum der Erdbevölkerung;
Modell im Deutschen Museum, München)

Es gibt in der Mathematik zwei Arten des Verständnisses:

1. man kann etwas handhaben (üblicherweise rechnen),

2. man hat ein anschauliches Verständnis gewonnen bzw. die grundlegenden

(meist geistesblitzartig-knapp formulierbaren)

 Zusammenhänge verstanden.

Manchmal aber bezweifle ich, dass man 1. wirklich

(d.h. verlässlich korrekt)

kann, wenn nicht 2. zutrifft, und vielleicht rühren daher so viele Schülerprobleme.

Gleichzeitig muss aber ergänzt werden:

1. vgl.  : Mathematik ist oftmals Abstraktion, also nicht anschaulich verständlich

(und erstmal die mathematische Anwendung Quantentheorie!),

2. fehlt es ja oftmals nicht nur SchülerInneN an Anschaulichkeit bzw. einem Verständnis der Zusammenhänge, sondern auch LehrerInneN - oder zumindest mir.

"90 % Transpiration, 10 % Inspiration": wie oft ist es mir im Mathematikstudium so ergangen: ich habe gepaukt und gerechnet und gepaukt und gerechnet ... und konnte hinterher die Standardaufgaben lösen. Dennoch blieb alles letztlich unverstanden, und wehe, man hätte mir eine auch nur leise vom Weg abweichende Aufgabe gestellt.

Ganz selten aber machte es "Klick", und alles schnurrte bei mir in einer ganz simplen Erkenntnis zusammen, nämlich z.B.:

"»Funktionentheorie«, d.h., dass man sich auf den ersten zehn Seiten zurecht definiert, was »Holomorphie« sein soll, und dann 300 Seiten auskostet, was sich mit dieser Holomorphie so alles anstellen lässt."

Schade ist nur, dass man so viele Erkenntnisse, die man durchaus mal hatte, auch wieder vergisst

(womit ich keineswegs angelesenes Faktenwissen meine, das sowieso nur unnötig das Gehirn verstopft).

Z.B. kann ich mich zwar noch erinnern, dass ich mal eine wunderhübsch anschauliche physikalische Bedeutung des (mathematischen) Integrals gelesen habe, weiß aber nicht mehr, worin sie eigentlich bestand. Schade!

Eigentlicher Anlass für diesen Essay ist eine Textpassage, die ich letztens in dem Buch "Das informative Universum; Das neue Weltbild der Physik" von Hans Christian von Baeyer gelesen habe:

"Exponentielles Wachstum ist durch die besondere Eigenschaft gekennzeichnet, dass der letzte Eintrag größer ist als die Summe aller vorherigen Einträge. (Bei der exponentiell anwachsenden Folge, die man jeweils durch Verdopplung erhält, 1, 2, 4, 8, 16, 32, 64 ..., ist 4 größer als 1 + 2 und 8 größer als 1 + 2 + 4; 16 ist mehr als 1 + 2 + 4 + 8 und so weiter.)"

(... wobei "Eintrag" eine mathematisch ungewöhnliche Formulierung ist.

Selbstverständlich gilt Baeyers Satz nur für "Einträge" mit jeweils ganzzahlig-positivem, also "natürlichem" x.)

Und da dachte ich dann doch wirklich:

schade (peinlich?), dass ich das nicht wusste

Anders gesagt: ich unterrichte seit Ewigkeiten die Potenz- und Exponentialfunktionen, aber bei allem Wichtigem, was in meinem Unterricht rüberkommen mag, hat doch diese entscheidende Formulierung immer gefehlt, weil ich sie nicht kannte. Blamabel!

Hier zwischendurch einige Hintergründe:

1. Funktionen der Form y = xⁿ nennt man "Potenzfunktionen".

Wichtig dabei ist: im Funktionsterm xⁿ steht die Variable x in der Basis bzw. unten.

Beispiele: y = x²    , y = x³   , y = x⁴ ...

Nehmen wir davon nun die einfachste und auch bekannteste, also y = x² .

Die zugehörige Wertetabelle ist

x	-3	-2	-1	0	1	2	3
y = x2	9	4	1	0	1	4	9

und das zugehörige Schaubild die allseits bekannte (Normal-)Parabel

2. Funktionen der Form y = n^x nennt man "Exponentialfunktionen".

   Wichtig dabei ist: im Funktionsterm n^x steht die Variable x im Exponenten bzw. oben.

Beispiele: y = 2^x    , y = 3^x   , y = 4^x ...

Nehmen wir davon wieder die einfachste, also y = 2^x .

(... also genau die, die auch Hans Christian von Baeyer im oben zitierten Textausschnitt gewählt hat).

Die zugehörige Wertetabelle ist

x	-3	-2	-1	0	1	2	3
y = 2x	0,125	0,25	0,5	1	2	4	8

und das zugehörige Schaubild

Im Unterricht werden nun überdeutlich die Gemeinsamkeiten, aber auch Unterschiede der beiden Graphen durchgenommen:

Besonders wichtig ist nun aber das Verhalten der beiden Funktionen für positive x, also rechts.

Schauen wir uns dazu beide Funktionsgraphen einmal zusammen in einem Koordinatensystem an:

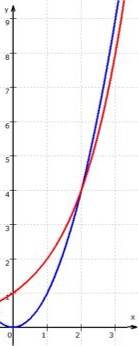
Daraus folgt:

1. für kleine x (zwischen 0 und 2) sehen die beiden Funktionsgraphen noch unterschiedlich aus, für größere x aber doch relativ ähnlich.

Zudem fällt auf:

• anfangs (links von 2) liegt der Graph der Exponentialfunktion noch über dem der Potenzfunktion,

• später
  (rechts von 2) liegt der Graph der Exponentialfunktion jedoch unter dem der Potenzfunktion.

Es folgt:

2. für große x wächst die Exponentialfunktion schwächer als die Potenzfunktion.

Wenn man nun einen kleineren Maßstab wählt, erhält man

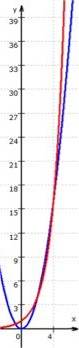
Daran wird deutlich, dass der 2. Schluss oben falsch war: für noch größere x (genauer: ab x = 4) liegt der Graph der Exponentialfunktion doch wieder

(und hier sei ohne Begründung ergänzt: endgültig)

über dem der Potenzfunktion.

(Immerhin haben wir hier schon einen entscheidenden Tipp: die beiden Funktionsgraphen für noch viel größere x zu untersuchen; s.u.)

Dennoch bleibt der Eindruck 1. bestehen:

für große x sehen die Graphen der Exponentialfunktion und der Potenzfunktion sehr ähnlich aus.

Und in der Tat haben sie da Gemeinsamkeiten: beide bilden dort Linkskurven und steigen somit immer stärker.

Insgesamt scheinen Exponential- und Potenzfunktionen bis auf kleine (lokale) Unterschiede also

• sowohl in der Funktionsschreibweise y = xⁿ bzw. y = n^x

• als auch in der graphischen Darstellung

sehr ähnlich zu sein.

Gerade diese vermeintliche Ähnlichkeit ist aber fatal:

• nicht nur, dass mit den beiden Funktionenarten vollständig unterschiedlich gerechnet wird

(was uns hier nur kurzfristig interessieren soll):

• die Lösung von Potenzfunktionen läuft auf Wurzeln,

• die von Exponentialfunktionen auf Logarithmen hinaus;

• kommt hinzu, dass Exponential- und Potenzfunktionen (in der Oberstufe) auch völlig unterschiedlich abgeleitet werden;

• sondern auch und vor allem: Exponential- und Potenzfunktionen verhalten sich auch für große x völlig unterschiedlich.

Oben genanntem Tipp folgend, können wir die Wertetabellen auch für größere x berechnen:

1. für die Potenzfunktion y = x² :

x	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10
y = x2	9	4	1	0	1	4	9	16	25	36	49	64	81	100

2. für die Exponentialfunktion y = 2^x :

x	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10
y = 2x	0,125	0,25	0,5	1	2	4	8	16	32	64	128	256	512	1024

Hier nun endlich zeigt sich für x größer oder gleich 4 (also in den gelb unterlegten Bereichen), dass

• die Exponentialfunktion anfangs (für x = 4) noch gleichauf mit der Potenzfunktion ist,
• aber danach für größere x erheblich schneller explodiert.

So anhand von Wertetabellen habe ich das auch immer mit SchülerInneN durchgenommen, und doch wird mir erst anhand des Baeyer-Zitats deutlich, wie man das noch viel besser oder zumindest zusätzlich verdeutlichen kann. Dazu nochmals der Kern des Baeyer-Zitats:

"Exponentielles Wachstum ist durch die besondere Eigenschaft gekennzeichnet, dass der [jeweils] letzte Eintrag größer ist als die Summe aller  vorherigen Einträge."

(Eine schöne Aufgabe bestünde nebenbei darin, allgemein zu beweisen, was Baeyer in seinem vollständigen Zitat nur anhand weniger Beispiele zeigt.)

Um das zu konkretisieren, schauen wir uns die Beispielsreihe von Baeyer nochmals genauer an:

• 4 größer als 1 + 2 = 3.

• 8 größer als 1 + 2 + 4 = 7

• 16 ist mehr als 1 + 2 + 4 + 8 = 15

Es sieht also so aus:

Der letzte Eintrag ist immer um genau 1 größer als die Summe aller  vorherigen Einträge.

(Ich spare mir hier mal die Überprüfung an weiteren Beispielen - und sowieso den Beweis.)

Zum Vergleich ist zu überlegen, wie der jeweils letzte Eintrag bei der Potenzfunktion y = x² von den vorherigen Einträgen abhängt.

(Kurz eingeschoben sei hier, dass es durchaus eine Regel gibt, wie sich bei der Potenzfunktion y = x² der letzte Eintrag aus dem [einen!] vorherigen Eintrag ergibt:

Die Folge der Abstände der y-Werte entspricht der Folge der ungeraden Zahlen.

x	0		1		2		3		4		5		6		7		8		9		10
y = x2	0	+1=	1	+3=	4	+5=	9	+7=	16	+9=	25	+11=	36	+13=	49	+15=	64	+17=	81	+19=	100

[Wiederum eine schöne Aufgabe wäre es, das allgemein zu beweisen.)

Anhand der Wertetabelle

x	0	1	2	3	4	5	6	7	8	9	10
y = x2	0	1	4	9	16	25	36	49	64	81	100

nun also einige Beispiele, wie sich bei der Potenzfunktion y = x² der jeweils letzte Eintrag zur Summe aller vorherigen Einträge verhält:

• 4 ist größer als           1

• 9 ist größer als           1 + 4                                                    = 5

• 16 ist größer als         1 + 4 + 9                                              = 14

• 25 ist KLEINER als   1 + 4 + 9 + 16                                      = 30
  (ein Verhältnis von etwa 1 : 1 )

• 36 ist KLEINER als   1 + 4 + 9 + 16 + 25                               = 55

• 49 ist KLEINER als   1 + 4 + 9 + 16 + 25 + 36                       = 91
  (ein Verhältnis von etwa 1 : 2 )

• 64 ist KLEINER als   1 + 4 + 9 + 16 + 25 + 36 + 49               = 140

• 81 ist KLEINER als   1 + 4 + 9 + 16 + 25 + 36 + 49 + 64        = 204

• 100 ist KLEINER als 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 + 81= 285
  (ein Verhältnis von etwa 1 : 3 )

• ...

Ich spare es mir (wieder) mir, hier eine allgemeine Regel herauszuarbeiten und gar zu beweisen.

Nur wird allemal deutlich:

Bei der Potenzfunktion y = x² ist der [jeweils] letzte Eintrag auf die Dauer erheblich  KLEINER als die Summe aller  vorherigen Einträge.

... wodurch nochmals klar wird:

für größere x explodiert die Exponentialfunktion erheblich schneller als die Potenzfunktion.

Nebenbei: ich vermute nach der Verhältnisfolge 1:1 - 1:2 - 1:3 sogar, dass bei der Potenzfunktion y = x² (allen Potenzfunktionen?) das Verhältnis zwischen

• dem letzten Eintrag und

• der Summe aller vorherigen Einträge

nicht nur immer kleiner wird, sondern sogar gegen Null geht - und das, obwohl, wie schon gesagt, die Potenzfunktion y = x²  auch immer stärker steigt.

Dieser Vermutung nach wäre das Wachstum der Potenzfunktion y = x² geradezu nichtig im Vergleich mit dem der Exponentialfunktion y = 2^x .

Erst Baeyers Feststellung

"Exponentielles Wachstum ist durch die besondere Eigenschaft gekennzeichnet, dass der [jeweils] letzte Eintrag größer ist als die Summe aller  vorherigen Einträge."

hat mir klar gemacht, wie massiv die Exponentialfunktion explodiert.

1. "größer als die Summe aller  vorherigen Einträge"

finde ich doch erheblich beeindruckender als das, was ich bei der Exponentialfunktion y = 2^x natürlich schon vorher wusste und gefährlich genug fand:

2. "doppelt so groß wie der [einzelne] direkt vorhergehende Eintrag."

(... wobei mir im Nachhinein durchaus klar ist, dass 2. auch 1. impliziert.)

Ich war halt vorher nie auf die Idee gekommen, alle vorherigen Einträge zu betrachten, und in sämtlichen mir bekannten geometrischen Darstellungen des Verlaufs exponentieller Funktionen

(z.B. beim berühmten Teichrosenbeispiel)

wird ja auch immer nur die Verdopplung gegenüber dem vorherigen Eintrag gezeigt, werden aber alle weiter zurückliegenden Einträge vergessen (übermalt).

Vielleicht liegt mein "Fehler" auch darin, dass ich bei Funktionen die geometrische Anschauung (!) zuungunsten der arithmetischen Betrachtungsweise überbetone (vgl. ).