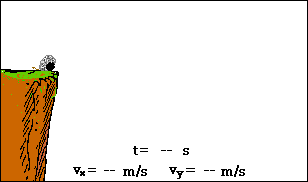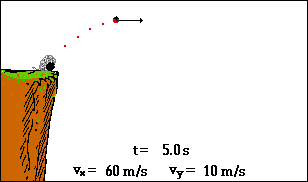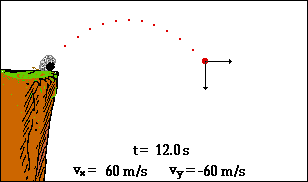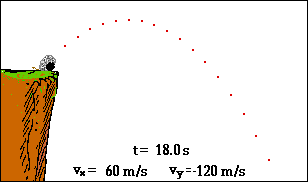
wie hätten Sie's denn gerne: scharf oder sanft?

... was ja letztlich eine Charakterfrage ist: ob man ein flotter Hüpfer oder doch nur ein Langeweiler ist

Die harmlosesten Funktionen sind sicherlich die linearen, also pillegraden, z.B.

y = 5•x + 7

 Man weiß verlässlich, wie sie in alle Ewigkeit weiter gehen werden, nämlich immer hübsch geradeaus

(wenn sie auch immerhin evtl. noch gleichmäßig fallen oder steigen).

Und unter den linearen Funktionen sind die konstanten Funktionen ganz besonders harmlos, z.B.

y = 0•x + 7

Sie bleiben auf ewig gleich, da tut sich gar nichts: ein ewiges Holland!

Allemal interessanter sind da schon die Potenzfunktionen höheren

(also zweiten, dritten ...)

Grades, z.B.

y = ax²

Da tut sich wenigstens noch was, da gibt es noch änderung statt Verdammnis zu ewiger Gleichheit.

Die wirklichen Knaller sind aber die Exponentialfunktionen, z.B.

y = 2^x

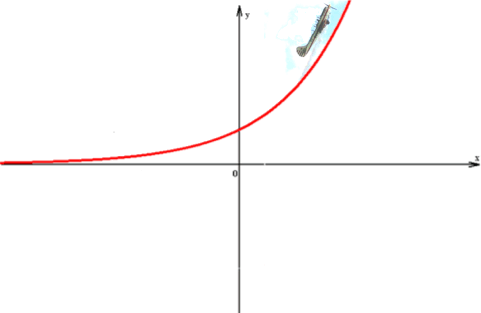
Das fängt (links) ganz harmlos an, ja, lange Zeit könnte man meinen, da herrschten holländische Langeweile und Verlässlichkeit, und gerade deshalb übersieht man allzu leicht und zu spät, wie's (rechts) irgendwann immer rasanter wird und dann so richtig Zoff in die Bude kommt.

Exponentialfunktionen steigen irgendwann über alle Maßen schnell, und zwar schneller als jede Potenzfunktion.

Z.B. überholt y = 2^x irgendwann sogar y = x¹⁰⁰⁰.

Nun, so lustig sind Exponentialfunktionen auch wieder nicht. Weil sie

• erst harmlos erscheinen

• und hinterher so rasant explodieren,

sind sie "in freier Wildbahn" sogar lebensgefährlich, nämlich etwa

• beim Wachstum der Erdbevölkerung

• oder bei der Kettenreaktion in einer Atombombe:

normalerweise sind Exponentialfunktionen nur durch Katastrophen zu stoppen.

Die Umkehrfunktionen der Exponentialfunktionen sind die Logarithmusfunktionen, und man erhält

(wie immer bei Umkehrfunktionen)

die Graphen der Logarithmusfunktionen, indem man die Graphen die Graphen der Exponentialfunktionen an der sogenannten "Winkelhalbierenden des 1. Quadranten" spiegelt:

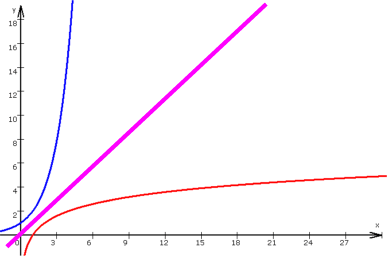
Wenn man sich nun nochmals die Exponentialfunktion genauer anschaut, so kann man daraus auch auf das Verhalten der Logarithmusfunktion schließen:

• die Exponentialfunktion (oder genauer: ihr Graph) geht

  • unendlich weit nach rechts,

  • aber erheblich schneller nach oben,

• also geht die Logarithmusfunktion

  • unendlich weit nach oben,

  • aber erheblich schneller nach rechts.

D.h. die Logarithmusfunktion wächst zwar extrem langsam, aber dennoch beliebig hoch

(wird also nie - wie es scheinen mag - parallel zur x-Achse).

Und dennoch steigen z.B. Hyperbelfunktionen

(nämlich z.B. y = - ¹/_x )

noch erheblich langsamer als Logarithmusfunktionen:

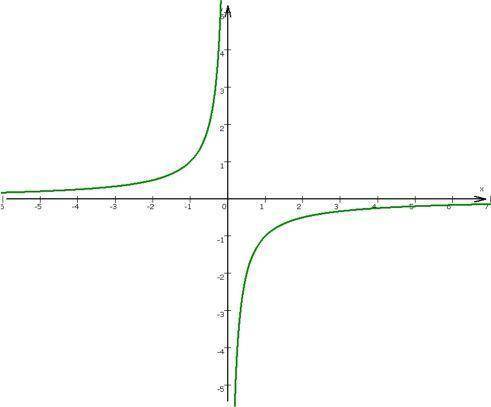
Es ist allemal bemerkenswert, was da rechts passiert: die Hyperbelfunktion

• steigt da zwar in alle Ewigkeit,

  • wird also nie parallel zur x-Achse

  • und geht schon gar nicht wieder nach unten,

• aber sie bleibt doch immer unterhalb der x-Achse,

• d.h. sie geht

  • zwar unendlich nah an die x-Achse heran,

  • aber sie erreicht sie nie
    (was man auch "asymptotisches Verhalten" nennt).