scheißegal - also möglichst einfach

Vgl.

1. Beispiel:

Angenommen, "wir" wollen begreifen, wie eine

(auch wenn wir diesen Fachbegriff noch gar nicht kennen)

exponentielle Vermehrung "funktioniert", und nehmen dazu der Anschaulichkeit halber das uralte Beispiel:

"Auf einem See befinden sich Seerosen, die sich jeden Tag verdoppeln."

(Nebenbei:

1. mit "verdoppeln" liegt schon eine enorme Vereinfachung vor:

• ggb. verdreifachen, vervierfachen ...
• und allemal ggb. ver-2,3-fachen ...)

Hier sei mal davon abgesehen, ob das Seerosen-Beispiel besonders lebensnah und/oder interessant ist

(immerhin ein bisschen interessanter ["aufgegeilt"] scheint es mir, wenn man die "Seerosen" durch "Killeralgen" ersetzt, die, wenn sie erstmal den gesamten See einnehmen, seine Sauerstoffzufuhr "abwürgen" und ihn damit "kippen" lassen, so dass alle Fische sterben).

Vielmehr zeigt sich an dem Beispiel schön ein Grundproblem von "Anwendungsaufgaben": sie lenken eher von der Mathematik (dem Prinzip) ab bzw. machen sie unsichtbar.

Hier nämlich, dass man systematisch drangehen kann, indem man verschiedene Anfangs- und Endwerte einsetzt - und mit möglichst einfachen anfängt.

üblicherweise werden in entsprechenden Matheaufgaben der Anfangswert sowie die Größe des Sees ebenfalls gleich mitgegeben, wird also alles "eigene Herangehen" von Anfang an unmöglich gemacht.

Wenn's ums Prinzip der Verdopplung geht, sind Anfangs- und Endwert doch letztlich - mit Verlaub - scheißegal, d.h., wir wählen möglichst einfache Werte, damit

1. das Prinzip besonders deutlich wird, sich also nicht hinter "krummen" Zahlen verbirgt,
2. nicht komplizierte Rechnungen vom Prinzip ablenken

(man vor lauter Bäumen [Rechnungen] den Wald [das Prinzip] nicht mehr sieht).

Nehmen wir also den denkbar einfachsten Anfangswert 1

(von mir aus auch - für Physiker - 1 m²),

und als Endwert (Seegröße) 10

(wieder für Physiker: 10 m²; nebenbei: mein kleiner Ausfall gegen Physiker ist hier durchaus mathematisch begründet: die Einschränkung auf Einheiten [m², cm² ...] lenkt mir schon wieder allzu sehr vom Prinzip ab).

Schnell (?) erhalten wir damit

Tag	Seerosen-fläche
0	1	20
1	2	21
2	4	22
3	8	23
4	16	24

Nebenbei: die letzte Spalte und damit das "Prinzip" bzw. die Funktionsgleichung y = x² erkennt man wohl nur dann, wenn man sogar zum Ausrechnen der allemal einfachen Ergebnisse zu faul ist

(z.B. 2 • 4 = 8),

sondern die "Verdopplungsreihe" unausgerechnet stehen lässt

(z.B. 2 • 2 • 2).

Obwohl oder gerade weil wir bewusst einfache Zahlen gewählt haben, deutet sich aber

(neben dem Finden des Prinzips, also der Funktionsgleichung)

schon das eigentliche Problem an:

• am dritten Tag ist die Seerosenfläche 8 groß, also noch kleiner als der See, d.h. der See ist noch nicht ganz voll;
• am vierten Tag wäre die Seerosenfläche bereits 16 groß, also größer als der See, und das heißt doch:
  • entweder wachsen die Seerosen über den Rand des Sees hinaus,
  • oder das Beispiel wird langsam schwachsinnig.

  (Nebenbei: in der Standardaufgabe wird üblicherweise als Frage am Ende ergänzt: "Wann ist der See voll?" - was ich auch schon wieder erkenntnisleitend, also erkenntnishemmend finde.)

Damit aber stellt sich doch (ohne Vorgabe) die Frage, wann

(irgendwo zwischen dritten und viertem Tag bzw. im Laufe des dritten Tages)

die Seerosen exakt den gesamten See einnehmen - und dann nicht mehr weiter wachsen (können).

Es sei hier nur erwähnt, dass sich damit der Logarithmus andeutet - und ein schaurig schiefer Wert heraus kommt.

Aber er wird so überdeutlich sichtbar und ist so erstaunlich, gerade weil wir mit sehr einfachen Werten begonnen haben.

Nun können (allzu) einfache Werte natürlich auch ein Irrweg sein bzw. wenig erkenntnisfördernd sein,

(z.B. ist die denkbar einfachste Zahl, nämlich 1, denkbar ungeeignet, um die Potenzrechnung zu lernen, denn da bleibt's doch streng langweilig:

• 1¹ = 1, 1² = 1, 1³ = 1, ..., 1ⁿ = 1,
• 1¹ = 1, 2¹ = 2, 3¹ = 3, ..., n¹ = n)

Und deshalb sollte man danach probeweise und sukzessive zu komplizierteren Werten übergehen , also z.B.

• Anfangswert 2 oder 2,75,
• Seegröße 17,
• weil die Natur oftmals nicht so nett ist, sich nach unserem Einfachheitsbedürfnis zu richten: die Seerosen vermehren sich jeden Tag ums 2,3-fache.

2. Beispiel:

Die "Hochzeit von Geometrie und Algebra" findet in der Schule in mehreren Schritten statt

(vgl. auch oder ):

• w/w/w: mit der Winkelsumme von 180⁰ in allen (ebenen Dreiecken) kann man drei Winkel miteinander in Beziehung setzen und beispielsweise den dritten, noch unbekannten Winkel berechnen, wenn man bereits zwei Winkel kennt.
• s/s/s: mit der Satzgruppe des Pythagoras kann man in rechtwinkligen Dreiecken drei Seiten miteinander in Beziehung setzen und beispielsweise die dritte, noch unbekannte Seite berechnen, wenn man zwei Seiten bereits kennt.
• Das schreit doch danach, dass man auch Mischformen von Winkeln und Seiten (also z.B. s/s/w ) berechnen möchte, also z.B. zu zwei bereits bekannten Seiten den (welchen?) noch unbekannten Winkel.

Eine solche Möglichkeit wäre es, den Winkel α mit seiner Gegenkathete und der Hypotenuse in Verbindung zu bringen

(... wobei die Begriffe "Gegenkathete" und "Hypotenuse" schon andeuten, dass wir hier - ohne Begründung - nur rechtwinklige Dreiecke betrachten [wie auch bei der Satzgruppe des Pythagoras]):

Vorerst ebenfalls noch ohne Begründung sei auch eine mögliche Gleichung genannt, die eine rechnerische Verbindung ausdrückt:

(Ich weiß also schon [und darauf wird unten zurückzukommen sein], worauf ich hinaus will.)

Da lauern doch gleich zwei Fragen:

1. Was bedeutet links eigentlich das "sin ( α )"? Und führen wir mit "sin ( α )" nicht etwas ganz Scheußliches ein?

(Bei der Winkelsumme und der Satzgruppe des Pythagoras konnten wir die Winkel bzw. die Seiten doch so hübsch einfach allein mittels Summen und Produkten in Verbindung bringen und brauchten darüber hinaus kein scheußliches Sonderzeichen wie eben "sin ( α )".)

2. Wieso wird rechts ein Bruch aus Gegenkathete und Hypotenuse gebildet? Das ist doch arg willkürlich und auch umständlich, wo doch beispielsweise auch eine simple Summe oder ein einfacheres Produkt aus beiden hätte gebildet werden können

(... wie - nochmals - bei der Winkelsumme und der Satzgruppe des Pythagoras).

Anders gesagt: in der 10. Klasse, in der sowas üblicherweise durchgenommen wird, kommen mit dem Sinus und dem Logarithmus besonders fies abstrakte "Sonderzeichen".

Verschieden große, aber immer rechtwinklige Dreiecke zum Winkel α könnte man in verschieden große Kreise einzeichnen, also beispielsweise

  

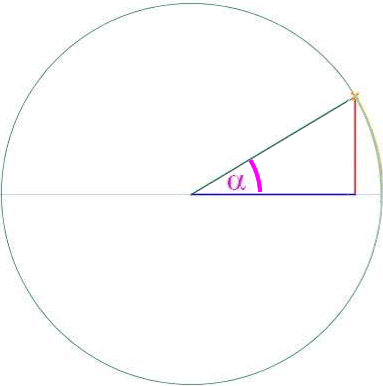
Um aber überhaupt erstmal an einem möglichst einfachen Beispiel Überblick zu gewinnen, wählen wir (scheißegal!) von all diesen möglichen Kreisen den denkbar einfachsten, nämlich den mit dem Radius 1, auch "Einheitskreis" genannt

(einer Maßeinheit, die hier allerdings größer als ein Zentimeter ist, damit die Zeichnungen nicht allzu klein werden):

 

Und hier im Einheitskreis taufen wir die rechte Strecke, also die Gegenkathete des Winkels α , auf den schönen Namen "Sinus von α " oder kurz "sin ( α )".

(Dabei ist die Namenswahl zwar eigentlich beliebig, hätten wir das frischgeborene Kind also z.B. auch "Knurzelchen" nennen können. Und doch macht der Name "Sinus" Sinn, sieht die - hier nicht näher erklärte - Sinusfunktion

nämlich buchten- oder busenförmig aus, und der lateinische Begriff "Sinus" bedeutet auf Deutsch eben "Bucht/Busen".)

Mit der neuen Namenswahl erhalten wir also

Wohlgemerkt: die Gegenkathete und damit der sin ( α ) hat nur im Einheitskreis das spezielle Maß und würde in kleineren/größeren Kreisen natürlich kleiner/größer ausfallen (s.u., wenn wir andere Dreiecke behandeln).

Überhaupt sollten wir vorgewarnt sein: alles, was beim Einheitskreis gilt, könnte auch tatsächlich nur da, aber nicht bei kleineren/größeren (rechtwinkligen) Dreiecken bzw. Kreisen und schon gar nicht bei allen (rechtwinkligen) Dreiecken/Kreisen gelten!!!

Mit der neuen Bezeichnung sin ( α ) ergibt sich nun aber im Einheitskreis

bzw. um das Mittelglied gekürzt und umgedreht genau die bereits oben genannte Gleichung

.

Immerhin wissen wir jetzt bereits, was sin ( α ) eigentlich ist, nämlich die Gegenkathete im Einheitskreis, und deren Länge könnten wir ja ablesen.

(Aber nochmals: bislang gilt all das ausschließlich im Einheitskreis, und ganz offensichtlich fällt die Länge der Gegenkathete ja in kleineren/größeren Kreisen auch kleiner/größer aus.)

Und inzwischen ist auch klar, weshalb wir überhaupt den umständlichen Bruch aus Gegenkathete und Hypotenuse bilden:

weil ja die Hypotenuse im Einheitskreis gerade 1 lang ist, wird der Bruch besonders einfach: da durch die simple Zahl 1 geteilt wird, verschwindet der anfangs "schwierige" Bruch umgehend wieder.

(Nochmals: auch das gilt wieder nur im Einheitskeis!

Nebenbei: wir werden unten allerdings noch einen anderen Grund für den Bruch kennenlernen.)

Kommen wir damit zu anderen (größeren/kleineren) Dreiecken, die allerdings auch rechtwinklig sind und den Winkel α haben.

Hier nun wenden wir einen enorm wichtigen mathematischen Trick an: wir zeichnen (zusätzlich) ein x-beliebiges anderes solches "Probedreieck", NENNEN WIR ABER NIE SEINE KONKRETEN MASSE

(während das mit eingezeichnete Dreieck im Einheitskreis natürlich feste Maße hat).

Weil wir aber in der gesamten folgenden Argumentation nie die konkreten Maße des "Probedreiecks" benutzen, muss das, was wir für dieses "Probedreieck" herausfinden, tatsächlich auch für alle anderen Dreiecke gelten (vgl. auch ):

Nun gilt nach einem (hier nicht näher erklärten) Strahlensatz:

Das Verhältnis (und deshalb der Bruch!) der Gegenkathete zur Hypotenuse ist also im großen Dreieck genau DASSELBE wie im Einheitskreisdreieck, und wir wissen ja bereits, dass im Einheitskreisdreieck gilt:

Also gilt in JEDEM Dreieck

(das rechtwinklig mit dem Winkel α  ist)

Wohlgemerkt: natürlich sind in kleineren/größeren Dreiecken die Gegenkatheten bzw. Hypotenusen größer/kleiner, aber ihr VERHäLTNIS  ist doch immer DASSELBE wie im Einheitskreisdreieck, nämlich sin ( α ).

Es reicht also, sin ( α ) im Einheitskreis herzuleiten - und die Ergebnisse davon sind eben doch (wider anfängliches Erwarten) auf alle Dreiecke übertragbar!

PS: Nun muss man ja nicht immer mühsam und ungenau nachmessen, wie groß der sin ( α ) zu einem Winkel α (im Einheitskreis!!!) ist, sondern kann man einschlägigen Tabellen oder auch dem Taschenrechner entnehmen,

• welcher sin ( α ) zu einem Winkel α
• und welcher Winkel α umgekehrt zu einem sin ( α ) gehört.

PPS: Nicht geklärt sei hier, weshalb wir den Sinus einzig und allein an rechtwinkligen Dreiecken definieren. Nur soviel: auch das dient der Vereinfachung/Vereinheitlichung.

Nun haben die beiden bislang genannten Beispiele allerdings einen entscheidenden Nachteil:

ich weiß ja schon vorweg, welches "Prinzip" sichtbar werden soll, und gehe deshalb wohl allzu zielgerichtet vor.

Deshalb gehe ich hier mal ein "Problem" an, das auch mir relativ neu ist, nämlich das statistische Notationsverfahren des

Boxplots.

(LehrerInnen sollten sich viel öfter selbst beim Lernen beobachten - oder überhaupt noch/wieder selbst lernen.)

Dabei kann ich aber natürlich wieder nicht verleugnen, dass ich schon gewisse Vorkenntnisse über markante statistische Verteilungen habe - und daher nur untersuchen möchte, wie sie sich in Boxplots spiegeln, d.h. welche Aussagekraft Boxplots für solche speziellen Verteilungen haben.

Mein Ziel ist es also zu beobachten, wie sich möglichst einfache statistische Verteilungen in Boxplots "niederschlagen" und was die verschiedenen Boxplots nun über die zugrundeliegenden Verteilungen aussagen.

Ich nehme dazu möglichst (in der Schule) alltägliche Beispiele, nämlich die Verteilung von Klassenarbeitsnoten

(aus gewissen Gründen sollen in der Klasse immer 18 SchülerInnen sein).

Verschiedene Fälle sind da

1. der übliche Ausfall, also annähernd die "Glockenkurve" :

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	1	3	5	5	3	1

2. arg übertrieben ein Ausfall, den ich ähnlich ein einziges Mal in einer Klasse hatte:

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	9	0	0	0	0	9

D.h. da "zerbricht" eine Klasse regelrecht:

• die eine Hälfte ist permanent unter-,
• die andere Hälfte permanent überfordert,
• und was soll der Lehrer nun tun, um alle zu erreichen?

(Binnendifferenzierung, individuelle fürderung :-)

3. wieder übertrieben ein Ausfall, den ich letztens mal ähnlich in einer Klasse hatte:

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	3	3	3	3	3	3

4. eine "linkslastige" Verteilung:

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	4	4	3	3	2	2

5. eine Verteilung mit zwei "Ausreißern":

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	8	8	0	0	0	2

6. ein wohl utopisches, aber doch gleichzeitig das denkbar schönste Ergebnis

(hoffentlich nicht nur für die Schüler-, sondern auch für LehrerInnen; vgl. ):

sämtliche SchülerInnen haben eine 1 geschrieben:

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	18	0	0	0	0	0

7. eine (und die einzige) völlig (?) unregelmäßige Verteilung:

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	1	7	0	3	5	2

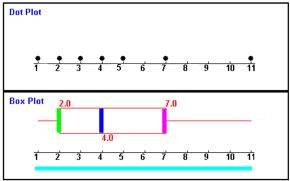
Und jetzt schauen wir uns mal an, wie sich das in den entsprechenden Boxplots niederschlägt

(wobei ich hier weglasse, wie diese Boxplots konstruiert werden; ich verwende der Einfachheit halber ja auch ein Boxplot-Progamm

- was man allerdings unbedingt erst tun sollte, nachdem man einige Boxplots per Hand gezeichnet, also begriffen hat, was der Medien sowie das obere und untere Quartil sind, wie sie also ermittelt werden):

1. zu

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	1	3	5	5	3	1

Hier zum ersten und einzigen Mal:

1. es ist immer zusätzlich oben ein "Dotplot" abgebildet, das noch mal sehr schön die Verteilung der Noten anzeigt, so dass man besser mit dem darunter liegenden Boxplot vergleichen kann;
2. in allen hier vorliegenden Beispielen ist die Spannweite 6 - 1 = 5, da immer sowohl die beste als auch die schlechteste Note, also 1 bzw. 6, vorkommt. Denkbar wäre allerdings etwa auch, dass beispielsweise die beste erreichte Note einer Klassenarbeit 2 und die schlechteste 5 wäre, die Spannweite also 5 - 2 = 3 betragen würde;
3. die farblichen Markierungen sind in allen Beispielen einheitlich

• unteres Quartil,
• Median
• oberes Quartil.

Damit aber nochmals zu

1. das Boxplot (samt Median) ist genauso symmetrisch wie die Verteilung,
2. mit dem Boxplot häufen sich 50 % der Werte zwischen 2,5 und 4,5 und die restlichen Werte liegen außerhalb dieses Bereichs.

2. zu

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	9	0	0	0	0	9

1. das Boxplot (samt Median) ist wieder genauso symmetrisch wie die Verteilung, aber
2. es nimmt die gesamte Spannweite ein, d.h. mindestens 50 % (genauer genommen sogar 100 %) der Werte liegen zwischen 1 und 6.

3. zu

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	3	3	3	3	3	3

1. das Boxplot (samt Median) ist wieder genauso symmetrisch wie die Verteilung,
2. es ist breiter als im 1. Fall, da die Werte gleichverteilt sind und sich nicht (wie im 1. Fall) in der Mitte häufen.

4. zu

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	4	4	3	3	2	2

1. das Boxplot liegt nicht mehr genau in der Mitte, sondern ist wegen der linkslastigen Verteilung nach links verrutscht.

5. zu

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	8	8	0	0	0	2

1. das Boxplot liegt wegen der starken Häufung der Werte (1en und 2en) links ebenfalls ganz links (also nicht symmetrisch), aber
2. der Median liegt in ihm ganz rechts, ist also identisch mit dem oberen Quartil, was sehr schön die radikalen, wenn auch seltenen Ausreißer (6en) rechts zeigt.

6. zu

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	18	0	0	0	0	0

Was nun aber soll diese Anzeige des Computerprogramms bedeuten?:

1. wegen der totalen Linkslastigkeit (ausschließlich 1en) liegt das Boxplot ebenfalls (ähnlich wie in 5.) ganz links, aber
2. es hat die Breite 0, was auch heißt: oberes Quartil, Median und unteres Quartil sind identisch.

7. zu

Note	1	2	3	4	5	6
Anzahl der SchülerInnen	1	7	0	3	5	2

1. zwar liegt das Boxplot wieder in der Mitte,
2. aber hier wird noch deutlicher als in Fall 5, dass der Median nicht in der Mitte des Boxplots (in der Mitte zwischen den beiden Quartilen) sein muss;
3. hier, also bei einer unregelmäßigen Verteilung, wird's fast am interessantesten:
   • das Boxplot liegt genau in der Mitte, wodurch deutlich wird, dass im linken Bereich ähnlich (!) viele Werte liegen wie im rechten;
   • aber der Median liegt nicht in der Mitte des Boxplots, sondern ist nach rechts verrutscht, weil rechts eben doch mehr Werte als links liegen.

Erst jetzt, nachdem ich anhand einfachster Verteilungen die wichtigsten möglichen Effekte von Boxplots kennengelernt habe, sehe ich mich in der Lage, selbst eine Verteilung zu konstruieren, die zu einem besonders aussagekräftigen Boxplot führt

(und wir werden dabei sehen, dass mir erst im Laufe dieser Eigen-Konstruktion Wichtiges an den Boxplots aufgeht, obwohl ich die reine Machart doch längst verstanden hatte).

Mein Ziel ist es, eine (relativ) einfache Ungleichverteilung der Abschnitte zu erreichen:

• die Strecke A vom untersten Wert der Zahlenreihe (und der sei der Einfachheit halber 1) bis zum unteren Quartil (bei ¹/₄ der Zahlenreihe) soll 1 lang sein,
• die Strecke B vom unteren Quartil bis zum Median (bei ¹/₂) soll 2 lang sein,
• die Strecke C vom Median bis zum oberen Quartil (bei ³/₄) soll 3 lang sein,
• die Strecke D vom oberen Quartil  bis zum Ende der Zahlenreihe soll 4 lang sein.

Das zugehörige Boxplot sieht also folgendermaßen aus:

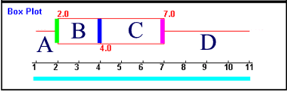
Wie so oft in der Mathematik, musste also am einen Ende verkompliziert werden, um am anderen Ende zu vereinfachen:

• um eine einfache Ungleichverteilung (Abschnittlängen 1, 2, 3 und 4) zu erreichen,
• musste die "schwierige" Spannweite 10 in Kauf genommen werden.

Man kann es auch so sagen: das Notenspektrum der Klassenarbeit ist nicht mehr 1 bis 6 bzw. - wie in der Oberstufe - 1 bis 15 Punkte, sondern 1 bis 11.

Es ergibt sich also in

:

• unteres Quartil bei 2,
• Median bei 4,
• oberes Quartil bei 7.

Um nun eine Verteilung zu erhalten, bei der die Quartile und der Median hübsch einfach liegen, ist eine "7-stufige" Verteilung nötig:

	1/4		1/2		3/4
1	2		4		7	11

Bemerkenswert daran ist nun, dass die  gelben Stellen beliebig mit Zwischen- oder gleichen Zahlen ausgefällt werden können, also z.B.

1

2

2

4

4

7

11

oder

1

2

3

4

5

7

11

Hier aber wird schon entscheidendes an Boxplots sichtbar:

Damit - besonders einfach - jeder Wert nur einmal vorkommt, wähle ich die zweite Verteilung, also

1

2

3

4

5

7

11

(nebenbei: im vorliegenden Fall haben also 1 + 2 + 3 +4 + 5 + 7 + 11 = 33 SchülerInnen die Klassenarbeit mitgeschrieben)

 und es ergibt sich nun tatsächlich - wie geplant - folgendes Boxplot:

Was nun aber besagt unser derart zurechtkonstruiertes Boxplot

?:

• dass sich in dem engen Bereich A das erste Viertel aller Werte drängelt,
• dass sich in dem schon ein wenig breiteren Bereich B das zweite Viertel aller Werte befindet,
• dass sich in dem nochmals breiteren Bereich C das dritte Viertel aller Werte befindet,
• dass zuguterletzt in dem breitesten Bereich D das letzte Viertel der Werte vorkommt

(... ein "Trend", der allerdings auch schon am zugehörigen "DotPlot" erkennbar war: links knubbelt es sich, während rechts zunehmend mehr "Luft" zwischen den Werten ist).

Oder kurz gesagt:

Ich empfinde es daher nach wie vor als irritierend an Boxplots,

• dass da in besonders breiten (engen) Bereichen nicht - wie man meinen könnte - besonders viele (wenige) Werte liegen,
• sondern dass da ganz im Gegenteil besonders wenige (viele) Werte liegen, diese da also besonders weit (eng) gestreut sind:

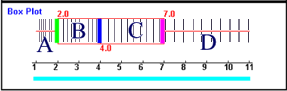
Insgesamt lässt sich also festhalten:

1. anhand sehr einfacher Verteilungen lässt sich viel über mögliche Formen von Boxplots lernen, aber
2. nur bei unregelmäßigen Verteilungen ist das Umgekehrte der Fall, geben die Boxplots also interessante Aufschlüsse über das Verhalten sonst unübersichtlicher Verteilungen.

Nach den ersten einfachen Beispielen wäre es nun also dringend an der Zeit, die Boxplots auf unregelmäßige und sehr große Datenmengen anzuwenden, weil sie erst da etwas zeigen, was man an den Verteilungen selbst nicht auf Anhieb sieht, nämlich sozusagen "Trends" der Verteilungen.

Dazu aber "müssen" Boxplots - wie gezeigt - gewisse Zwischenwerte unterschlagen: man erkauft sich die Trend-Erkenntnis mit Ungenauigkeit, d.h.

Nun gibt es auch andere Verfahren, um Trends herauszustellen

(z.B. Mittelwert oder Varianz),

aber bei all diesen Verfahren gehen zugunsten des Trends einige Informationen verloren.

Der Vorteil der Boxplots gegenüber all diesen anderen Verfahren ist, dass Boxplots besonders einfach

(durch Abzählen der Viertel)

erhältlich sind.

Und ein spezieller Vorteil des Medians ggb. dem Mittelwert ist, dass der Median

(was hier nur erwähnt, nicht hergeleitet sei)

weniger empfindlich gegenüber "Ausreißern" ist.