seltsame Zusammenhänge:  

Zwischen den verschiedenen Gleichungen

• für das KugelVolumen:   (r) = π r³
• für die KugeloberFläche: (r) =  4 π r²
• für die KreisFläche:         (r) =    π  r²
• für den KreisUmfang:       (r) = 2 π  r

gibt es erstaunliche Ähnlichkeiten:

1. und allemal am wichtigsten, aber doch auch erstaunlichsten, dass das Volumen, die Flächen und der Umfang alle in Abhängigkeit von r berechnet werden können

(immerhin ist klar, dass alle abhängig von r ab- bzw. zunehmen),

wobei man sich allerdings leider (?) als Koeffizienten die hübschhässliche Zahl π ≈  3,14159265358979 einhandelt.

Dabei wächst

• das KugelVolumen   (r) = π r³            mit der dritten   Potenz von r, also        sehr rasant,

(wenn r doppelt so groß ist, ist (r)       acht       mal so groß), 

• die KugeloberFläche (r) =  4 π r²         mit der zweiten Potenz von r, also                 rasant,

(wenn r doppelt so groß ist, ist (r)        vier       mal so groß),  

• die KreisFläche         (r) =    π  r² auch mit der zweiten Potenz von r, also auch        rasant,

(wenn r doppelt so groß ist, ist (r)          vier       mal so groß),   

• der KreisUmfang        (r) = 2 π  r                      linear                 mit r, also                 gleichmäßig

(wenn r doppelt so groß ist, ist  (r) auch doppelt mal so groß). 

Entsprechend ergeben sich verschieden stark steigende Graphen

(hier nicht maßstabsgetreu):

2. - und das folgt aus 1. -, dass in allen Gleichungen dieselben "Grundsubstanzen" π und r auftauchen,
3. , dass es aber auch noch andere seltsame Gemeinsamkeiten gibt, nämlich

• die 4 in der ersten und zweiten sowie
• die 2 in der zweiten, dritten und vierten Gleichung.

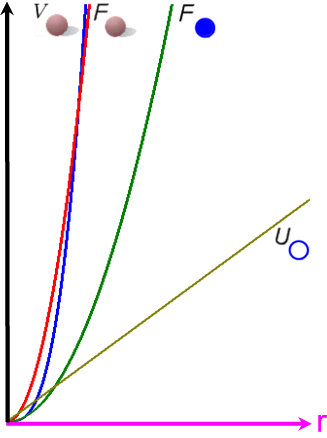
Seltsam ist es aber für mich vor allem, dass es mir, der ich doch einen Blick für Ableitungen haben sollte, erst heute siedend heiß aufgeht, wie diese Gemeinsamkeiten zustande kommen:

1. (r) ' =      (r),
2. (r) =   4 • (r),
3. (r) ' =       (r).

Daraus folgt außerdem:

4. (r) '' =   (r).

Davon sollen uns im folgenden die reinen  Ableitungsgleichungen interessieren:

1. (r) ' =      (r), 
2. (r) ' =       (r)
3. (r) '' =   (r),

Wenn die Ableitung die momentane Veränderung misst, so bedeutet das doch:

1. (r) zeigt, wie sich                                  (r) in Abhängigkeit von r verändert,
2.   (r) zeigt, wie sich                                   (r) in Abhängigkeit von r verändert,
3. (r) zeigt, wie sich die Veränderung von (r) in Abhängigkeit von r verändert

(... wie sich also eine Veränderung verändert).

Was aber mag man sich unter solchen Veränderungen (von Veränderungen) vorstellen?

Schauen wir uns dazu die Graphen nochmals (vergrößert) im Koordinatensystem dar:

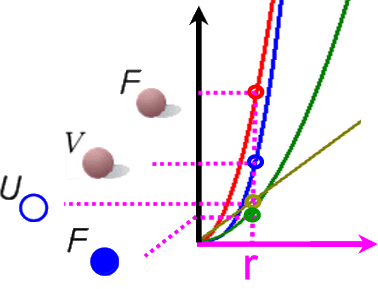
Hier kann man nun gut ablesen, wie groß für ein fixes r die Eigenschaften (r) , (r) , (r) und (r)  sind.

Interessant wird all das aber erst, wenn

• r nicht mehr fix ist, sondern sich verändert,
• bzw. wenn die zugehörigen Kugeln und zugehörigen Kreise sukzessive größer werden,

also

(wie so oft; vgl. )

in Bewegung.

Dabei gilt im Folgenden:

• r wird gleichmäßig größer

(also z.B. nacheinander r = 1,9, r = 2, r = 2,1 ...),

• unter dem  Augenblick r  wird jener Augenblick verstanden, in dem r beim Wachsen eine gewisse Größe (z.B. r = 2) annimmt, wobei es
  • kurz vorher noch kleiner (z.B. r = 1,9999) war
  • und kurz nachher bereits größer (z.B. r = 2,0001) sein wird.

Damit ergibt sich: 

1. = ein Viertel der Geschwindigkeit der Veränderung von im Augenblick r  ;
2. = Geschwindigkeit der Veränderung von im Augenblick r  .

Und aus A.  und B. folgt "doppelt gemoppelt"

3. = ein Viertel der Geschwindigkeit der Geschwindigkeit der Veränderung von im Augenblick r  .

Oder anders gesagt:

= ein Viertel der Beschleunigung von im Augenblick r  . 

Der Kreisumfang (r) in einem bestimmten Augenblick r zeigt uns also, wie schnell sich gerade die Kugeloberfläche (r) verändert und wie sehr das Kugelvolumen (r) beschleunigt.

Und dennoch bleibt das alles für mich völlig abstrakt: ich kann mir beim besten Willen nicht vorstellen, was das überhaupt anschaulich bedeuten soll: dass

• der Kreisumfang
• ein Maß für die Beschleunigung (???)
• des Kugelvolumens ist.