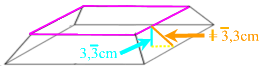
für die Rechnung in 2. hatte ich noch hinzugefügt, dass die Höhe h des Pyramidenstumpfes 3,3 cm lang sei, was allerdings noch - das hatte ich sogar noch dabei gesagt - mittels eines Strahlensatzes herzuleiten sei.

"Meine" SchülerInnen wissen, was das bedeutet: man darf mit h = 3,3 cm weiter rechnen, wenn man es nicht selbst herleiten kann, aber die volle Punktzahl gibt es nur, wenn man es eben auch herleiten kann.

Im Nachhinein frage ich mich, ob dieser "Höhentipp" sinnvoll war:

• einerseits ist er im 2. Aufgabenteil für viele SchülerInnen natürlich sehr hilfreich,
• andererseits verfährt er aber

(wenn SchülerInnen geradezu wider Erwarten die ganze Aufgabe lesen, bevor sie loslegen)

zu einem Fehler im 1. Aufgabenteil: einem absehbaren Fehler, um den es mir hier vor allem geht.

Wie denn baut man den im 1. Aufgabenteil geforderten "Restkörper"? Da gibt es (mindestens) zwei Möglichkeiten:

1. , indem man anfangs

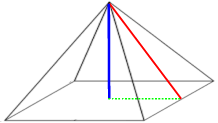
die vollständige Pyramide

baut, sie allerdings noch nicht zusammenklebt. Man zeichnet also zu allererst die "Abwicklung"

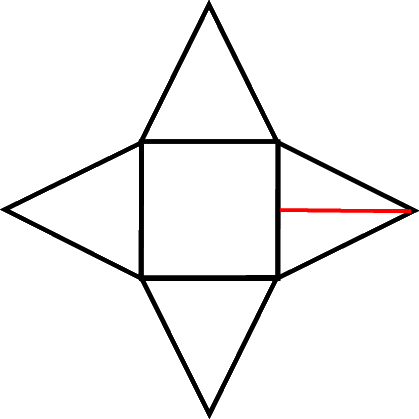
Schon hier ist aber ein typischer Fehler vorprogrammiert: die höhen h_d der Dreiecke sind nicht identisch mit der Höhe h = 10 cm der Pyramide, sondern müssen erst (und zwar mit dem Satz des Pythagoras) berechnet werden.

Man muss also - und so gibt eins das andere - rechnen, bevor man zeichnet bzw. bastelt.

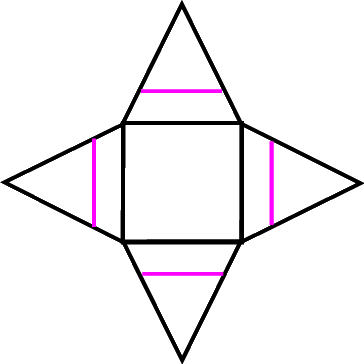
Nun kann man zu den Seiten des Quadrats 10 cm lange Parallelenstücke (Seiten des "Stecheisens") zeichnen

und dann die Reste wegschneiden:

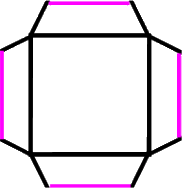
Das Ergebnis

klappt man nun zu einem

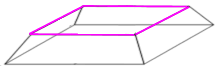
Pyramidenstumpf

zusammen, in den man dann "nur" noch die Seitenwände des Lochs einbauen muss, wonach man zuguterletzt noch das Bodenloch entfernt.

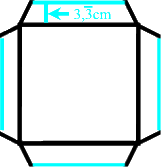
Nebenbei: die Seitenwände des Lochs haben nun tatsächlich die vorgegebene Höhe h_L = 3,3 cm, aber das muss man nicht mal wissen, sondern kann man per "Augenmaß" hinkriegen.

Der (zweite bzw. im Grunde derselbe) typische Fehler wäre aber, Streifen der Breite 3,3 cm zu zeichnen:

Denn

2. Möglichkeit:

weil man die Dreieckshöhen nicht berechnen möchte oder kann, fängt man erst gar nicht mit der gesamten Pyramide an, sondern gleich mit dem Pyramidenstumpf, indem man

• entweder (richtig) 10 cm lange Parallelenstücke zu den Quadratseiten zeichnet

,

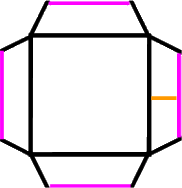wozu man allerdings die Breite der so entstehenden Streifen braucht, die wieder nur rechnerisch (mit dem Strahlensatz) erhältlich ist;

• oder (falsch; s.o.) einen 3,3 cm breiten Rand an die Quadratseiten zeichnet

(zum weiteren Vorgehen s.o.).

So (1.) oder so (2.) muss man also rechnen, um basteln zu können, d.h. das Basteln ist nicht bloß Vorarbeit zum (Volumen-) Rechnen. Vielleicht verfährt aber der erste Aufgabenteil, der scheinbar nur Basteln verlangt, die SchülerInnen dazu, nur zu basteln und dazu nur die vorgegebenen Werte zu benutzen.

Und so oder so ist also die Gefahr groß, falsche Höhen zu benutzen.

Dass aber solche "Höhenfehler" massenhaft auftreten werden, weiß jedeR LehrerIn schon vorher. Warum aber eine Aufgabe stellen, die geradezu verlässlich von vielen SchülerInneN  sowieso nicht richtig gelöst wird? Nur um dieses Vor-Urteil zu bestätigen?

Natürlich muss man sich klar machen, warum der "Höhenfehler" so oft auftritt:

1. , weil da

• einerseits "reale", außen auf den Pyramidenschrägen zwar nicht eingezeichnete, aber doch messbare Höhen auftreten (rot und orange),
• andererseits "virtuelle", im Inneren der Pyramide liegende (blau und hellblau);

2. , weil evtl. "virtuelle" Hilfslinien gebraucht werden, die in der Aufgabenstellung gar nicht auftauchen (blau, orange)

(und man beachte, wie widersprüchlich 1. und 2. sind); 

3. aber auch, weil viele SchülerInnen große Schwierigkeiten haben, sich im Dreidimensionalen zu orientieren

(obwohl doch der dreidimensionale Modellbau gerade dazu dient, von den sonst immer nur zweidimensionalen und besonders missverständlichen Projektionen weg zu kommen).

Aus all dem folgt natürlich, dass diese "Virtualitätsproblematik" wie überhaupt dreidimensionaler Modellbau natürlich schon mal vorher im Unterricht aufgetaucht sein muss

(... und dennoch müssen auch Aufgaben möglich bleiben, die nicht genau so oder ähnlich im Vorunterricht aufgetaucht sind, sondern Transfer bzw. neue Überlegungen fordern).

Aber obwohl ähnliche Aufgaben in meinem Vorunterricht vorgekommen waren, werde ich das Gefühl nicht los, viele SchülerInnen in eine mir schon vorher allzu gut bekannte Falle gelockt zu haben.

Mir ist natürlich klar, dass man nicht alle absehbaren Fehler

(z.B. [a + b] ² = a ² + b ² )

von vornherein vermeiden kann und darf, denn dann würden ja sämtliche SchülerInnen nur noch Einsen schreiben

(wäre das eigentlich so schlimm?).

Aber ich meine ja sowieso nicht alle möglichen Fehler, sondern "nur" die Standardfehler, also diejenigen, die viele SchülerInnen immer wieder machen.

Die aber muss man auch immer wieder - und möglichst anschaulich - im (Vor-)Unterricht behandeln, um sie eben doch (seien wir bescheiden:) ein wenig mehr zu verhindern.

Vor allem aber muss man wissen, aus welchen guten Gründen viele SchülerInnen sie immer wieder machen.