typisch Mathematik: n² + n + 41 ist für JEDES n eine Primzahl
(wobei "für jedes n" bedeutet: für jede natürliche Zahl 1, 2, 3, 4 ... bis in alle Ewigkeit)

... oder der Versuch, (scheinbar) an den Haaren herbei Gezogenes doch noch dadurch interessant zu machen, dass man es durchdringt.

BEHAUPTUNG: auch reine Innermathematik ohne jede Anwendung kann Spaß machen - und vielleicht kann der folgende Text genau dies BEWEISEN.

Vorsicht: Etikettenschwindel!

An der Behauptung

"n² + n + 41 ist für JEDES n eine Primzahl"

ist so viel "typisch Mathematik", dass man sie geradezu als Musterbeispiel für mathematische Denkweisen ansehen könnte:

1. Die Aussage "n² + n + 41 ist für JEDES n eine Primzahl" ist ausgesprochen simpel: egal welche natürliche Zahl n ich in "n² + n + 41" einsetze, es kommt immer eine Primzahl

(also eine Zahl, die [ohne Rest] nur durch 1 und sich selber teilbar ist)

dabei heraus.

Also z.B.

4² +  4 + 41= 61, und 61 ist in der Tat eine Primzahl,
7² +  7 + 41= 97, und 97 ist in der Tat eine Primzahl.

2. Die Aussage "n² + n + 41 ist für JEDES n eine Primzahl" ist eine "All-Aussage": die Behauptung betrifft ALLE n, d.h. da wird behauptet, dass IMMER eine Primzahl heraus kommt, egal welche der UNENDLICH VIELEN natürlichen Zahlen n ich da einsetze.

Solch eine "All-Aussage" ist mehr als nur "typisch Mathematik", sondern zeichnet die Mathematik sogar vor allen anderen Wissenschaften aus: NUR die Mathematik kann Aussagen für unendlich viele bzw. alle Fälle machen - und beweisen.

3. Man ahnt vielleicht schon: die Aussage ist

(wie viele mathematische Aussagen, beispielsweise der berühmte "letzte Satz von Fermat")

sehr simpel, aber der Beweis könnte teuflisch schwierig werden.

(In der Mathematik hat man oftmals nur die Wahl,

• entweder leicht anzufangen und schwierig zu enden

• oder umgekehrt schwierig anzufangen und leicht zu enden.

Und das finde zumindest ich oftmals

• irritierend: wieso ist beispielsweise der Beweis des "letzten Satzes von Fermat" so teuflisch schwierig, obwohl der Satz doch so simpel ist?
  Ich kann mir nicht helfen: da misstraue ich dem Beweis und meine noch immer, dass er doch einfacher möglich sein müsste.

• atemberaubend schön: wie kommt es, dass ein anfangs kompliziertes Problem oftmals am Ende so leicht lösbar ist?)

Die Beweisschwierigkeit deutet sich immerhin schon an, wenn man bedenkt, was bei

"n² + n + 41 ist für JEDES n eine Primzahl"

zu zeigen wäre:

• eben doch für JEDE einzelne natürliche Zahl n (also für UNENDLICH VIELE Zahlen!), dass da jeweils eine Primzahl herauskommt;

• auf den ersten Blick hat man also UNENDLICH VIELE Rechnungen durchzuführen, wird also NIE fertig - und gibt es dann doch besser von Anfang an auf!?

Das schier Unglaubliche und fast schon Paradoxe ist aber, dass die Mathematik es in vielen Fällen dennoch schafft, "All-Aussagen" in endlicher Zeit und endlich vielen Schritten zu beweisen.

4. Die Aussage "n² + n + 41 ist für JEDES n eine Primzahl" scheint doch jedem Nicht-Mathematiker an den Haaren herbei gezogen:

1. "schön und gut, mag ja stimmen dass n² + n + 41 für JEDES n eine Primzahl ergibt, aber das ist mir doch herzhaft egal (etwa so wie jener berühmte Reissack, der in China umfällt)!"

Hier folgt schon doppelt: der Laie (SchülerInnen) hat ÜBERHAUPT KEINEN BEWEISWUNSCH, geschweige dass er die BEWEISNOTWENDIGKEIT sieht:

1. "Wieso soll ich beweisen, was mir völlig schnuppe ist?!"

2. "Wenn einE MathematikerIn es behauptet, wirds doch wohl stimmen."

(merke: widersprich nie einem Mathematiker, denn der behält letztlich doch immer penetrant recht!)

(Nebenbei: die Unterscheidung zwischen Beweiswunsch und Beweisnotwendigkeit scheint mir doch elementar: die MathematikerInnen behaupten immer eine Beweisnotwendigkeit, wo aus Laiensicht nicht mal ein Beweiswunsch vorliegt: der Laie hat gar keine Not, einen Beweis zu erfahren bzw. sogar selbst zu beweisen.

Schon gar nicht hat der Laie einen allgemeinen Beweiswunsch, und das auch noch für unendlich viele [alle] Fälle: im Alltag bleibt keine Zeit für massenhaft Fälle oder ist es völlig ausgeschlossen, sämtliche Fälle zu untersuchen. D.h. wir neigen im Alltag alle zu Verallgemeinerungen: wenn all die ca. 300 Türken, die wir bisher gesehen haben, schwarze Haare hatten, unterstellen wir [rechnen wir hoch], dass überhaupt alle 68 Millionen Türken schwarze Haare haben.

Und doch kann Mathematik mit der Frage nach wirklich allen Fällen wohltun, nämlich sich durch "Hochrechnungen" ergebende Vorurteile hinterfragen.)

2. mag der Laie immerhin noch sehen (oder sich erzählen lassen):

"mittels

»n² + n + 41 ist für JEDES n eine Primzahl«

erhalte ich massenhaft (unendlich viele!) Primzahlen"

(nämlich für jedes n eine andere Primzahl),

aber dann wird er sich doch vermutlich fragen:

"was habe ich von all diesen Primzahlen, wo stecke ich sie alle hin?!"

Ein Laie mag sich

(falls er ein erste Einblicke in die mathematische "Zahlentheorie" genommen hat)

zudem fragen:

"Warum eigentlich sind die MathematikerInnen so scharf auf Primzahlen - und gibt es eigentlich noch Nebensächlicheres in der Welt?"

3. "gehts überhaupt noch abgedrehter als ausgerechnet n² + n + 41, also

• diese Kombination aus "n²" und "n" und "41"!?

(wobei einE MathematikerIn allerdings sofort - wenn auch hier irreführend - an 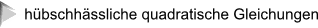denkt, die alle die Form

ax² +  b x +  c   
1n² + 1 n + 41

haben)

• und überhaupt diese ominöse Zahl 41 !?: warum nicht statt der 41 eine 5 oder eine 31 ?! Die 41 erscheint als nackte Willkür.

(Aber MathematikerInnen sind ja ach so schlau, sie werden sich bei ausgerechnet der 41 wohl irgendwas [???] gedacht haben. Vermutlich wollte da einE MathematikerIn doch nur mit der ganz schön großen Zahl 41 beeindrucken.)

Auf den Einwand b. (was also all dieses Gewese um Primzahlen solle) könnte man dem Laien natürlich antworten, dass Primzahlen nachweislich durchaus wichtig bei vielen Anwendungen in der Datenverschlüsselung (beispielsweise im elektronischen Geldverkehr) sind

(vgl. etwa  und   ).

Aber das ist doch eine typische Scheinantwort bzw. Schein-Selbstlegitimierung der Mathematik

(mindestens so aussichtslos wie der Versuch des Schulfaches Latein, seine Aktualität zu beweisen):

der Laie muss (und möchte) doch gar nicht wissen, wie seine Daten verschlüsselt werden, Hauptsache, es funktioniert.

(Und es funktioniert ja überhaupt nur, weil der Laie es nicht wissen muss, sondern es uneinsehbar-unkompliziert im Hintergrund läuft.)

Ein Laie wird vermutlich noch weniger das rein innermathematische Interesse von MathematikerInneN an Primzahlen verstehen bzw. nachvollziehen können:

• sie sind so simpel definiert

(diejenigen natürlichen Zahlen, die [ohne Rest] nur durch 1 und sich selbst teilbar sind)

• und haben doch ein höchst merkwürdiges "Eigenleben"

(vgl. :

• es lässt sich leicht beweisen, dass es unendlich viele davon gibt,

• dass sie aber, zu je größeren Zahlen man vordringt, im Schnitt immer seltener werden: halbe Ewigkeiten lang kommen gar keine mehr -

• und dann doch urplötzlich wieder "Primzahlzwillinge"

(Primzahlen wie z.B. 11 und 13, zwischen denen nur eine gerade, als Nichtprimzahl liegt).

Es ist, als würde man ewig lange durch die leeren "unendlichen Weiten des Weltalls" rasen, um dann urplötzlich doch wieder in einer Zwillingsgalaxie zu landen.

• es gibt zwar Abschätzungen, wie dicht die Primzahlen in gewissen Bereichen liegen, aber es ist noch keine Formel gefunden worden, mit der man alle Primzahlen bestimmen könnte.

Hier aber wird unsere Formel "n2 + n + 41" dann vielleicht doch staunenswert: mit  ihr erhalten wir zwar nicht alle Primzahlen (schon für das kleinste n = 1 ergibt sich  12 + 1 + 41 = 43. Nun ist 43 zwar eine Primzahl, aber damit haben wir die ersten Primzahlen 2,3,5,7,9 ... schon übersprungen, also nicht erfasst), aber immerhin doch unendlich viele (für jedes n eine).

5. Um auf den Beweis zurück zu kommen, dass "n² + n + 41" für JEDES n eine Primzahl ergibt.

Einen Beweiswunsch bzw. eine Beweisnotwendigkeit (s.o.) ergibt sich doch wohl überhaupt erst, wenn man eine Reihe von Beispielen ausgerechnet hat:

n	n2 + n + 41
1	43
2	47
3	53
4	61
5	71
6	83
7	97
8	113
9	131
10	151
11	173
12	197
13	223
14	251
15	281
16	313
17	347
18	383
19	421
20	461
21	503
22	547
23	593
24	641
25	691
26	743
27	797
28	853
29	911
30	971

Bei all diesen Beispielen ergeben sich rechts tatsächlich immer Primzahlen, und da wird man doch vermuten, dass das immer so weiter gehen, also auch für größere n immer eine Primzahlen ergeben wird.

Man merkt schon: der Rechenaufwand ist doppelt enorm:

1. musste für obige Liste 30 Mal n² + n + 41 ausgerechnet werden

(da gings doch schneller, mir ein kleines Computerprogramm zu schreiben, das die Werte ausspuckte),

2. musste natürlich immer noch überprüft werden, ob die Ergebnisse rechts tatsächlich Primzahlen sind. Auch das ist "per Hand" gar nicht so einfach, und deshalb habe ich in einer fertigen Primzahlliste nachgeschlagen.

Typische MathematikerInnen sind für so viele Rechnungen sowieso zu faul.

So langsam muss also

entweder ein allgemeingültiger Beweis her

(dass also bei "n² + n + 41" immer Primzahlen herauskommen).

Hier besteht die Gefahr, dass man sich ewig an einem solchen Beweis abmüht

• und ihn einfach nicht findet, obwohl die Behauptung stimmt

(laut Kurt Gödel gibt es sogar mathematische Behauptungen, die sich weder beweisen noch widerlegen lassen; und Alan Turing hat bewiesen, dass man das solchen Sätzen leider vorher nicht ansehen kann),

• oder vor lauter Beweisbetriebsblindheit nicht merkt, dass falsch ist, was man zu beweisen versucht;

oder ein einziges schnuckeliges kleines Gegenbeispiel

(irgendein n, so dass bei n² + n + 41 keine Primzahl herauskommt).

Solch ein Gegenbeispiel ist (wenn man es erst mal hat) eine feine Sache: ein einziges Gegenbeispiel bringt die gesamte großmäulige Behauptung zum Einsturz

(und zwar auch dann, wenn diese Behauptung für alle anderen Beispiele gelten würde).

Gegenbeispiele sind also hübsche kleine Sprengsätze!

(Ich habe mal einen semmelblonden und doch "waschechten" Türken kennengelernt!)

Das Problem ist nur das Kleingedruckte, also "wenn man es [ein Gegenbeispiel] erst mal hat":

• Wie findet man es? Es könnte ja immerhin sein, dass es sich sehr gut versteckt, also z.B. erst bei n = 10001 auftaucht, d.h. in einem Bereich, bei dem man längst entnervt aufgegeben hat

(weshalb man nie von einem Gegenbeispiel erfährt und deshalb in alle Ewigkeit fälschlich meint,  bei "n² + n + 41" kämen immer Primzahlen heraus).

• Nur schlechte Behauptungen gelten schon für das zweite oder dritte Beispiel nicht - und werden deshalb wohl erst gar nicht aufgestellt.

Es gibt 2 ¹/₂ Sorten Menschen:

• die erste Sorte unterstellt immer, dass wohl stimmt, was behauptet wird: diese Sorte Mensch ist umgänglich und liebenswürdig, aber manchmal auch allzu leichtgläubig;

• die zweite Sorte zweifelt an jeder Behauptung, widerspricht aus Prinzip und sucht gleich das Haar in der Suppe.

• MathematikerInnen (wie vermutlich die meisten Menschen) sind beides gleichzeitig:

1. sie suchen nach einer Bestätigung für eine Vermutung, bzw. umgekehrt ergeben erst viele zutreffende Beispiele die Vermutung, dass eine Behauptung immer gilt;

2.  gleichzeitig verhalten sie sich aber, wie sich laut dem Philosophen Karl Popper alle WissenschaftlerInnen verhalten sollten: sie suchen nach Gegenbeispielen.

6. Wir hatten oben gesehen, dass der Aufwand, dreißig bestätigende Beispiele zu berechnen, doppelt immens ist

(dreißig umständliche Rechnungen sowie dreißig Überprüfungen, ob die Ergebnisse Primzahlen sind).

So weit wird wohl kein Mensch rechnen wollen, sondern jeder wird wohl schon nach weniger Beispielen akzeptieren

(oder es MathematikerInneN einfach "abnehmen": "ich glaubs dir ja, aber lass mich damit bitte in Ruh"),

dass die Aussage

"n² + n + 41 ist für JEDES n eine Primzahl"

richtig ist.

Das Problem ist nur:

die Aussage "n2 + n + 41 ist für JEDES n eine Primzahl" ist NICHT richtig. Also war bereits die Überschrift dieses Textes ein Etikettenschwindel! ätsch!

Zwar ist n² + n + 41 noch für einige Zahlen mehr als oben ausprobiert eine Primzahl

(nämlich auch noch für n = 31 bis n = 39),

aber für n = 40 ist n² + n + 41 = 1681, und das ist KEINE Primzahl.

Denn 1681 ist

• keineswegs nur durch 1 und sich selbst, also 1681, teilbar,
• sondern auch durch 41 (1681 : 41 = 41 ohne jeden Rest).

Und prompt für das nächste n, also 41, ergibt sich 1763, was wiederum KEINE Primzahl ist.

Denn 1763 ist

• keineswegs nur durch 1 und sich selbst, also 1763 teilbar,
• sondern auch durch 41 (1763 : 41 = 43 ohne jeden Rest) und somit auch durch 43.

Auch das ist typisch, wenn auch nicht für "die" Mathematik bzw. alle MathematikerInnen, so doch für einige: solchen Schlaumeiern dient die Mathematik oftmals nur dazu, Laien reinzulegen - und sie in ihrer Leichtgläubigkeit zu beschämen, womit solche MathematikerInnen natürlich immer indirekt sagen:

"du bist dumm, ich aber bin schlau; jetzt hab also mal Respekt vor mir (wenn du mich schon nicht magst)!"

Der Gag besteht aber wohl darin, dass die Allermeisten (also auch diese Schlaumeier!) anfangs auf die falsche Behauptung reinfallen bzw. reingefallen sind.

(Ich auch!)

Diese Schlaumeier können den Gag also erst erzählen, nachdem auch sie selbst nachträglich gemerkt haben, dass die Regel wider erstes Erwarten nicht immer funktioniert (und warum nicht; s.u.). Da mögen sie sich doch bitte nicht so besserwisserisch gehaben!

(Aber beruht nicht fast jedes Lachen über Witze auf der Erleichterung darüber, nicht [mehr] selbst der Dumme zu sein - gerade weil man es sich selbst durchaus zutrauen würde bzw. es sogar selbst mal war?: "wer zuletzt lacht [nicht mehr der Dumme ist], lacht am besten")

Aber nicht alle MathematikerInnen sind so arrogant, und die Behauptung "n² + n + 41 ist für JEDES n eine Primzahl" wurde vermutlich nicht mal zum Reinlegen geschaffen. Sondern dahinter steckte wohl eher das theoretische Interesse (s.u.).

(Kurz eingefügt sei ein entscheidender pädagogischer Nachteil der Aussage

"n² + n + 41 ist für JEDES n eine Primzahl".

Sie soll ja wohl dazu dienen, dass

• man Ewigkeiten lang [mit guten Gründen!] das Falsche vermutet

• und erst dann das Richtige sieht.

D.h. sie soll vor voreiligen Schlüssen warnen. Nur haben wir soeben gesehen, dass doch wohl kein "Normalsterblicher" jemals sämtliche Ergebnisse für n = 1 bis n = 40 bzw. n = 41 ausrechnen wird. D.h. die Aussage verpufft pädagogisch, bevor sie überhaupt einsetzen kann.)

7. Damit stellen sich so langsam zwei Fragen:

1. Warum ergibt n² + n + 41 immerhin für n = 1 bis n = 39

(also für eine erstaunlich lange Serie)

tatsächlich Primzahlen?

2. Warum ergeben sich bei n² + n + 41 für n = 40 und n = 41 KEINE Primzahlen mehr - und hätte man (?) das nicht vielleicht doch von Anfang an sehen können?

("wenn man vom Rathaus zurück kommt, ist man schlauer", d.h.

• einige werden natürlich [fälschlich] behaupten, es schon immer gewusst zu haben,

• einige sehen sowas vielleicht wirklich von Anfang an,

• aber immerhin kann man ja nachträglich rausfinden, woran man es von Anfang an hätte erkennen können)

Obwohl bzw. gerade weil also für "n² + n + 41 ist für JEDES n eine Primzahl" kein Beweis möglich ist (da sich da ja - wie gezeigt - keineswegs immer Primzahlen ergeben), stellt sich jetzt eine andere "Beweisnotwendigkeiten", die wieder "typisch Mathematik" ist:

Man (?) möchte verstehen, warum etwas (nicht) funktioniert.

Dabei sei dringend darauf hingewiesen: ich habs anfangs auch nicht gesehen, dass n² + n + 41 für  n = 40 und 41 KEINE Primzahlen mehr ergibt, ich bastele das mir auch erst im Nachhinein zusammen

(... und hätte doch mit ein wenig zahlentheoretischer Vorerfahrung bei der Ankündigung eines allgemeingültigen "Kochrezepts" für Primzahlen hellhörig werden müssen. Hätte, hätte, hätte!).

Hellhörig bin ich erst geworden, als klar wurde, dass "n² + n + 41" ausgerechnet für n = 41 KEINE Primzahl, sondern 1763 = 41 · 43 ergibt.

Warum? Für n = 41 ergibt sich

    n ² +  n + 41 =

= 41² + 41 + 41 ,

und daran ist dann doch endlich auffällig, dass die 41 in allen Summanden vorkommt.

Anders gesagt: man kann die 41 auch mittels des Distributivgesetzes aus allen Summanden rausziehen bzw. ausklammern:

    41² + 41 + 41 =

= (41  +  1  +  1 ) · 41

Dabei ist es eher nebensächlich, dass (41  +  1  +  1 ) = 43 ist, dass also die Klammer den zweiten Faktor 43 ergibt

(denn nochmals 1763 = 41 · 43).

Oder anders gesagt (und wieder typisch mathematisch): interessant

• sind nicht konkrete Zahlen

(hier die 43),

• sondern was da grundsätzlich passiert:

eben dass die 41 mittels Distributivgesetz ausklammerbar ist.

Im Nachhinein wundert einen das alles auch gar nicht mehr:

selbstverständlich

• lässt sich ausgerechnet die 41 aus allen Summanden ausklammern, weil diese 41 eben von Anfang an auch im letzten Summanden stand;

• ergibt also "n² + n + 41" für n = 41 KEINE Primzahl mehr.

Wir können also (wieder typisch mathematisch) verallgemeinern:

Die Überlegungen zur 41 helfen uns nun herauszufinden, dass auch für n = 40 KEINE Primzahl herauskommt:

in der allgemeinen Form "n² + n + 41" ist es zwar nicht möglich, etwas aus allen drei Summanden auszuklammern. Also fangen wir mit dem Ausklammern bei den ersten beiden Summanden an, in denen ja beides Mal ein n vorkommt.

    n² + n      + 41 =   

= (n  + 1)· n + 41

Aus dem Gesamtausdruck (inkl. der 41 hinten) kann man nun aber 41 dann etwas ausklammern, wenn

1. entweder (n + 1)

2. oder n

 41 ist, also wenn

1. entweder n = 40

2. oder        n = 41

(ich erlaube mir hier aus Platzgründen, solche Feinheiten des in der Tat ja durchaus schwierigen Distributivgesetzes nicht genauer zu erklären).

Während nun also klar ist, weshalb für n = 40 und n = 41 KEINE Primzahlen zustande kommen (Frage b.), bleibt (zumindest mir vorerst) unklar, weshalb sich für n = 1 bis n = 39 die gezeigte Serie von Primzahlen ergibt (Frage a.). Ist das purer Zufall, oder liegt das an der spezifischen Struktur des Ausdrucks "n² + n + 41"? Anders gefragt: wurden die besonderen Eigenschaften von "n² + n + 41" zufällig gefunden, oder ließ sich dieser Ausdruck konstruieren?

(Denn beispielsweise für n² + n + 31", wobei 31 ja immerhin auch eine Primzahl ist, kommt bereits für n = 1 eine Nicht-Primzahl, nämlich 33 = 3 · 11 zustande.)

Mir scheint, dass das Beispiel "n² + n + 41" überhaupt "nur" aus drei Gründen gewählt wurde:

1. , weil es für eine lange Serie (n = 1 bis n = 39) tatsächlich Primzahlen liefert, also ein feines Beispiel dafür vorliegt, dass man in der Tat erst eine Serie vermuten könnte, ihr aber dennoch nicht trauen sollte.

... und ich kenne kein anderes mathematisches Beispiel, das so lange scheinbar "gut" geht - um dann endlich doch "schief" zu gehen.

2. , weil jemand (im Gegensatz zu mir) sofort gesehen hat, wann aus n² + n + 41 etwas ausklammerbar ist, wann also keine Primzahl vorliegt.

3. siehe 8.

8. Zuguterletzt nochmals die bereits oben gestellte Frage:

Wieso eigentlich die 41 in "n² + n + 41", d.h. geht es auch mit anderen Zahlen?

... also wieder die typische mathematische Frage nach Verallgemeinerungsmöglichkeiten.

Die Antwort überlasse ich ohne Begründung dem Programm "WinFunktion":

Beispielsweise erzeugt also (rot umrandet) auch n² + 29n + 251 eine Serie von Primzahlen (für n = 1 bis n = 25), aber die blau umrandete Kombination zeigt:

41 scheint die kleinste Zahl zu sein, bei der die Form die besonders einfache Form 1· n2 + 1 · n + c eine schöne Primzahlserie ergibt (und zwar für c = 41).

An den Beispielen aus "WinFunktion" sieht man nun auch das oben schon genannte theoretische Interesse: da wollte jemand - wieder: typisch Mathematik - ganz allgemein wissen,

• welche Kombinationen der Form

a n² + b n + c

• wie lange Primzahlserien ergeben.

Bzw. vermutlich war ihm (weshalb?) aufgefallen, dass gerade diese Kombinationen schöne Primzahlketten erzeugen.

9. Die Behauptung "n² + n + 41 ist für JEDES n eine Primzahl" ist mir irgendwo zugeflogen, und ich habe anfangs bewusst nicht nach ihren Hintergründen gesucht, sondern wollte der Behauptung selbst beikommen.

Erst im Nachhinein erfahre ich, dass es kein Geringerer als

Leonard Euler (1707-1783),

war, der "n² + n + 41" samt den oben gezeigten Eigenschaften als erster behandelt hat.