
oder
Mathematiker ticken anders

Die im Folgenden besprochene Aufgabe wird im üblichen Schulunterricht wegen
des Stoff- und Klausurendrucks wohl (wenn überhaupt) nur in höchstens einer
Schulstunde, also 45 Minuten, durchgenommen (!) werden können
(und wenn, dann nur der erste Teil mit p =
, aber garantiert nicht die Verallgemeinerung im zweiten Teil).
Bei solch kurzer Behandlung ist aber natürlich nicht die Fülle
der Ãœberlegungen möglich, die unten zur Lösung der Aufgabe aufgezeigt
werden.
Die Folge ist, dass Schüler "sowas" im besten Fall für eine Klausur
auswendig lernen - und direkt danach wieder vergessen.
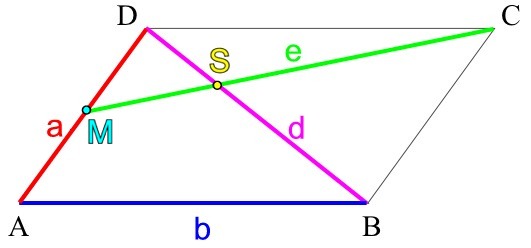
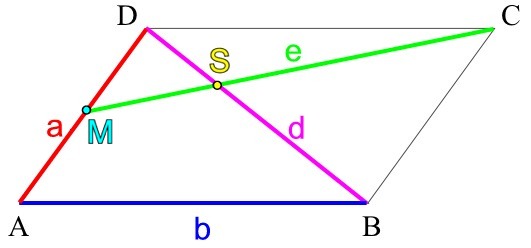
Gefragt ist nun bei
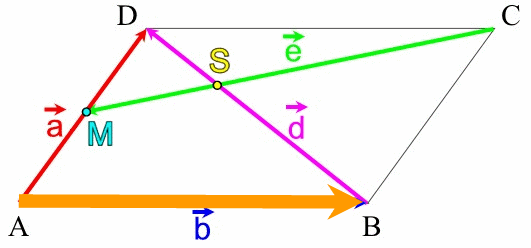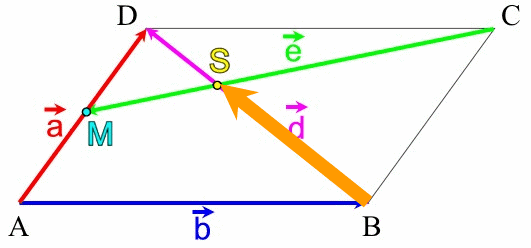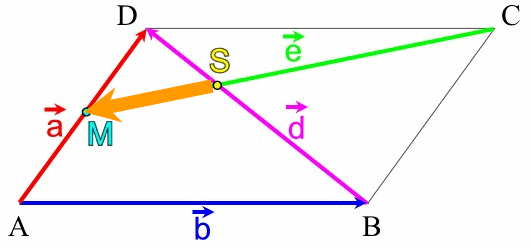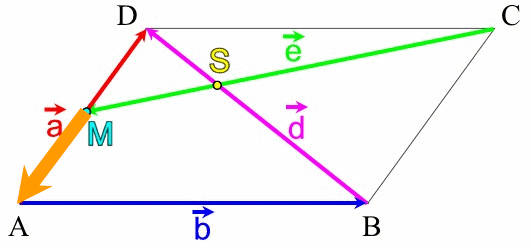
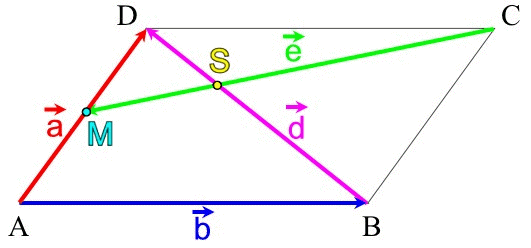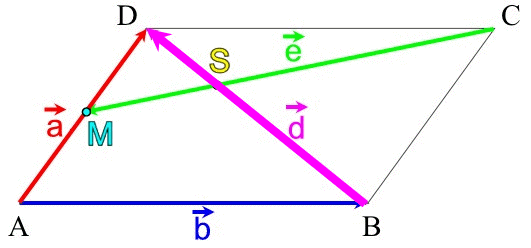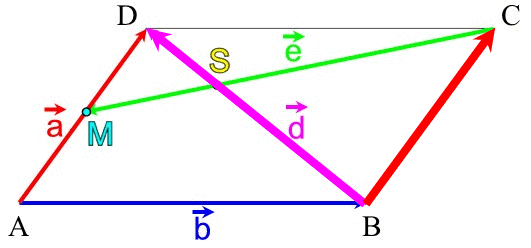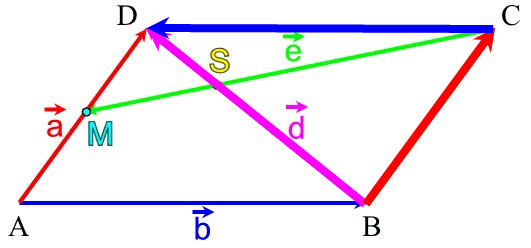
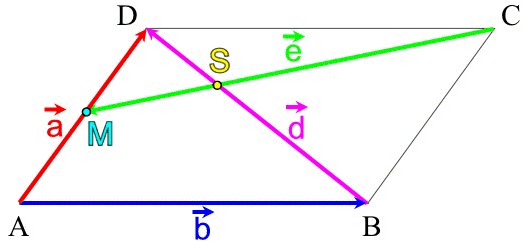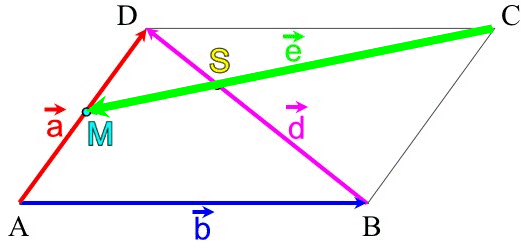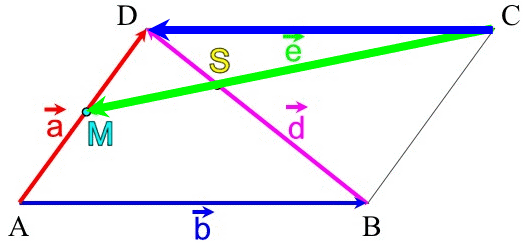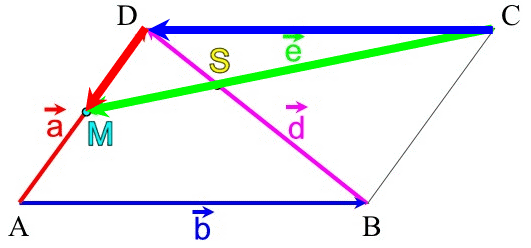
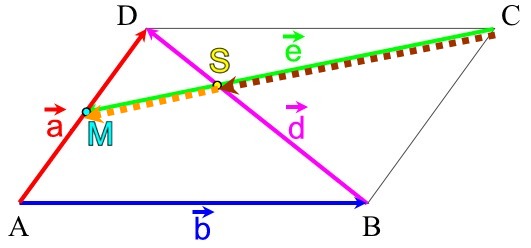
(Planskizze eines beliebigen Parallelogramms, woran also
- nicht die konkreten Maße [Streckenlängen und Winkel] wichtig sind,
- sondern
- dass eben ein Parallelogramm vorliegt, also gegenüberliegende Seiten parallel sind,
- wie die Strecken d und e sich aus den Punkten des [beliebigen] Parallelogramms ergeben
[M als Mittelpunkt der Strecke a ],
- eigentlich banal, aber dennoch, wie wir unten sehen werden, von zentraler Bedeutung: dass die benachbarten Seiten a und b nicht auch noch parallel sind, weil sie dann überhaupt kein Parallelogramm aufspannen würden:

;
oder schon vektorgeometrisch gesagt: dass die beiden Vektoren
und
NICHT KOLLINEAR
sind.
Das ist so banal, dass ein Laie es vermutlich gar nicht bedenken würde, während Mathematiker es zum zentralen Argumentationselement machen [s.u.].
Und ebenso banal und doch mathematisch wichtig: dass keine der beiden Seiten a und b die Länge Null hat, wodurch ja ebenfalls kein Parallelogramm entstünde
... woran man mal wieder sieht, wie andersartig Mathematiker denken:
- Laien würden wohl sagen, dass
sind,
- Seiten der Länge Null gar keine Seiten und
- Parallelogramme der Höhe  Null gar keine Parallelogramme
- während für Mathematiker
- Seiten der Länge Null nur Spezialfälle aller Seiten und
- Parallelogramme der Höhe Null nur Spezialfälle aller Parallelogramme
sind.Ãœberhaupt differenzieren Mathematiker sehr genau bei dem, was im Volksmund unterschiedslos "nichts" oder "kein" heißt: es kann
- "null" bedeuten, wenn z.B. eine Gleichung sehr wohl eine Lösung hat, aber eben die Zahl 0;
- "leere Menge" bzw. { } bedeuten, wenn z.B. eine Gleichung gar keine Lösung bzw. null Lösungen hat
[das bedeutet nebenbei nicht, dass Null eine Lösung ist, denn dann hätte die
Gleichung mit der Null ja doch eine Lösung];
- "Eins" bedeuten, wenn vor einer Variablen keine Zahl steht: x = 1x,
- "mal" bedeuten, wenn zwischen zwei Termen kein Rechenzeichen steht: 3 x = 3•x.
[und um die Verwirrung vollständig zu machen: bei aus ganzen Zahlen und Brüchen
"gemischten Zahlen" wie z.B.bedeutet der Leerraum hingegen ein +].)
 ,
,
(im Schnittpunktteilen.)
Einem Mathematiker reicht das alles allerdings nicht:
dass er sehr krumme Streckenverhältnisse, also nicht das einfache (und korrekte) Streckenverhältnis 1:2 gefunden hätte
(was ihm vermutlich herzhaft egal wäre);
(einem Laien wäre solche Ungenauigkeit vermutlich wieder schnurzpiepegal, bzw. er empfände eine Genauigkeit auf vier Stellen hinter dem Komma wohl nur als Haarspalterei);
(eben weil nur bei diesem das Verhältnis 1 : 2 auftritt);
bei anderen Parallelogrammen hingegen träten andere Streckenverhältnisse auf
(unser Laie könnte da sagen: "ich wollte, nein: sollte es ja eh nur für dieses eine Parallelogramm herauskriegen, und was interessieren mich alle = unendlich viele Parallelogramme dieser Welt?!"
Nebenbei: im Schulunterricht liegt es nahe, gar kein Parallelogramm vorzugeben, sondern die Schüler beliebige Parallelogramme zeichnen, ausmessen und dann die entsprechenden Streckenverhältnisse berechnen zu lassen: um so erstaunlicher ist es dann, dass immer dasselbe Verhältnis herauskommt!).
Anders gesagt: ein "richtiger" Mathematiker schätzt allemal Planskizzen und Zeichnungen als Veranschaulichungsmöglichkeiten: mit ihnen kommt man oftmals überhaupt erst auf Vermutungen.
Aber Mathematiker sind auch skeptisch gegenüber Zeichnungen, weil diese
Das heißt nun nicht, dass Mathematiker vollständig auf Zeichnungen (und damit Anschaulichkeit!) verzichten, sondern sie wenden einen "salomonischen" Trick an. Im vorliegenden Fal:
(alle [also unendlich viele!] Parallelogramme zu zeichnen, wäre auch arg viel Arbeit, und zudem wären viele davon mikroskopisch klein oder gigantisch groß;
nebenbei: das gezeichnete Parallelogramm sollte keine "Somdermaße" haben, also z.B. nicht rechtwinlig [ein Quadrat oder Rechteck] sein, da unser Beweis sonst hinterher eventuell unbemerkt nur für solche Parallelogramme mit Sondermaßen gilt),
(aber auch Messungenauigkeiten irrelevant sind).
Wir machen zum allgemeinen Parallelogramm nur eine einzige weitere
Vorgabe:
![]() halbiert die Seite
a (in jedem Parallelogramm).
halbiert die Seite
a (in jedem Parallelogramm).
Es lohnt sich allemal, Aufgabenstellungen genau zu lesen:
(was bei der vorliegenden Aufgabe allerdings nicht der Fall ist; dafür ist aber natürlich der Unterrichtskontext ein Tipp:
- wenn die vorliegende Aufgabe im Unterrichtskontext "Vektorgeometrie" gelöst werden soll, ist die elementargeometrisch gestellte Aufgabe wohl vektorgeometrisch zu lösen und also überhaupt erstmal in die Vektorgeometrie zu übersetzen
[hier zeigt sich allerdings exemplarisch ein typisches Problem des deutschen Schulunterrichts: es werden fast immer nur Aufgaben zum gerade anstehenden Unterrichtsthema gestellt, und als Folge davon können deutsche Schüler auch nur höchstens solche Aufgaben lösen];
- und wenn gerade geschlossene Vektorzüge anstehen, ist die Aufgabe wohl mit eben diesen zu lösen
[fast unlösbar scheint mir allerdings das Problem, wie man selbstständig auf geschlossene Vektorzüge als probaten Lösungsweg kommen kann;
nebenbei: es gibt wohl noch ganz andere Lösungswege zur vorliegenden Aufgabe:
da in der vorliegenden Aufgabenstellung von einem Verhältnis (Singular) die Rede ist, wird bereits vorweg unterstellt, dass
- der Schnittpunkt
die Strecke d in demselben Verhältnis teilt wie die Strecke e,
- also
 ,
,was doch
(und das ja ist der eigentliche Witz der Aufgabe bzw. ihre einzige Existenzberechtigung!)
wegen der verschiedenen Definitionen von
- d [Verbindung der beiden Eckpunkte B und D des Parallelogramms] und
- e [Verbindung des Eckpunkts C mit einem Seitenmittelpunkt
]
keineswegs auf Anhieb selbstverständlich erscheint.
Wenn man die Aufgabe in Vektorgeometrie übersetzt, ergibt sich z.B.
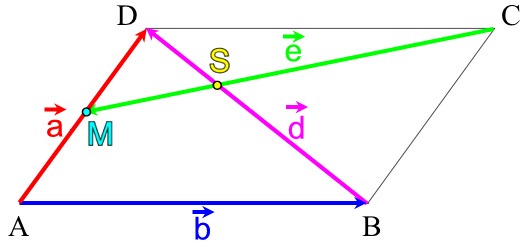
Die beiden Vektorenn
![]() undd
undd
![]() spannen
also das Parallelogramm ABCD auf. Dadurch entsteht
spannen
also das Parallelogramm ABCD auf. Dadurch entsteht
Weil sich aus den beiden Vektoren
![]() und
und
![]() automatisch die Vektoren
automatisch die Vektoren
![]() und
und ![]() ergeben,
nennt man
ergeben,
nennt man
![]() und
und
![]() auch "Basisvektoren": wenn
auch "Basisvektoren": wenn
![]() und
und
![]() vorgegeben sind, ist damit die Basis für das gesamte
Parallelogramm und all dessen "Innereien" (inkl.
vorgegeben sind, ist damit die Basis für das gesamte
Parallelogramm und all dessen "Innereien" (inkl.
![]() und
und ![]() ) gelegt.
) gelegt.
Diese Erkenntnis werden wir unten ausnutzen, wenn wir alle anderen
vorkommenden Vektoren durch die beiden Basisvektoren
![]() und
und
![]() ausdrücken.
ausdrücken.
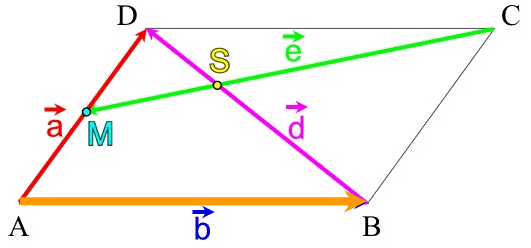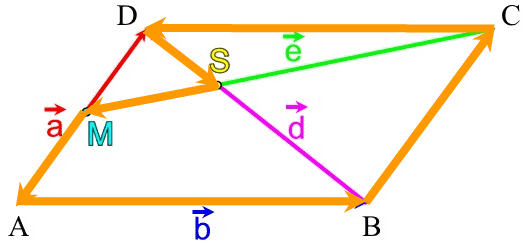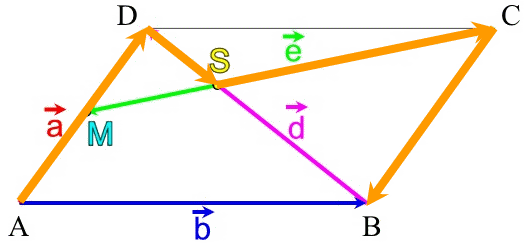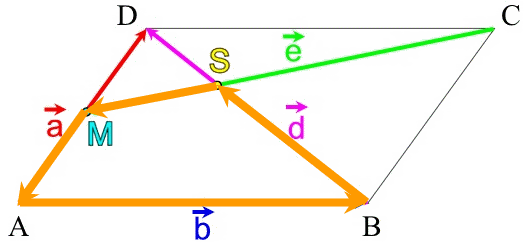 ,
,(man könnte ein wenig makaber auch sagen: wenn ich imm selbenn Krankenhauss sterbe, in dem ich geboren wurde, hätte ich der Einfachheit halber auch die ganze Zeit in eben diesem Krankenhauss bleiben können - und waren die verschiedenen möglichen Lebenswege [außerhalb des Krankenhauses] letztlich alle gleichermaßen unnötige Ummwege).
Solche geschlossenen Vektorzüge müssen zwei Minimalbedingungen erfüllen:
(wenn mir z.B. von B nach D durchgeradeaus hindurch laufen würden, wäre das dasselbe, als wenn wir von B nach D ohne Betrachtung von
gingen;
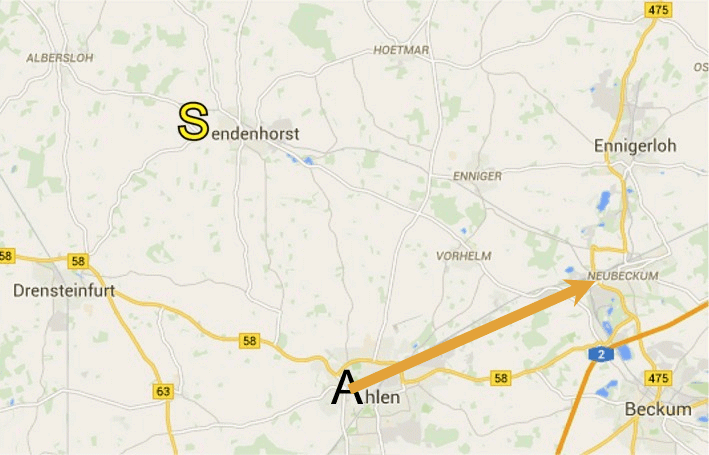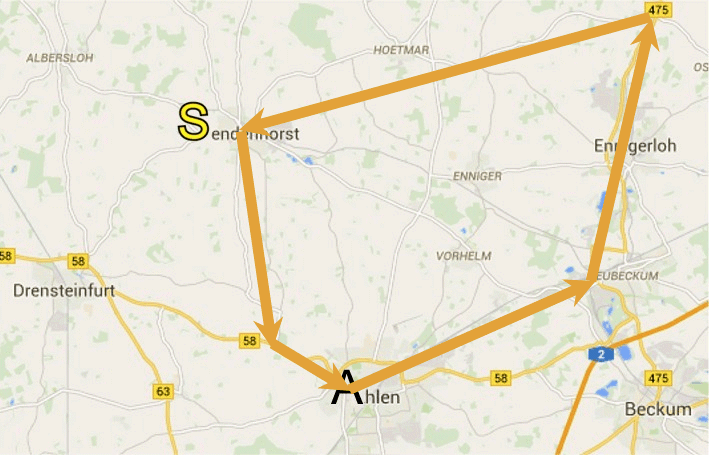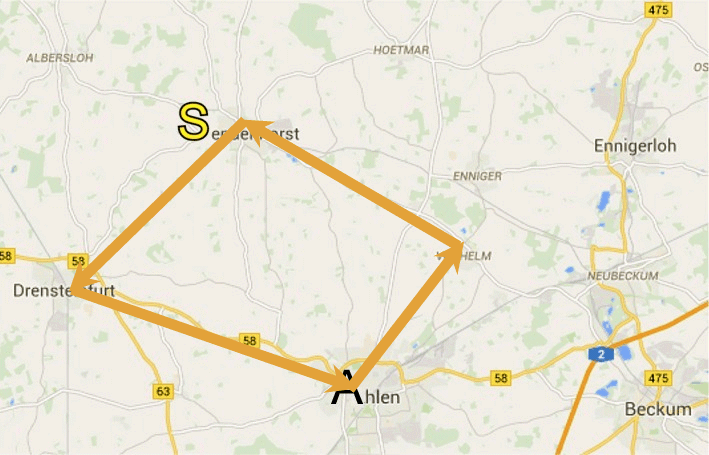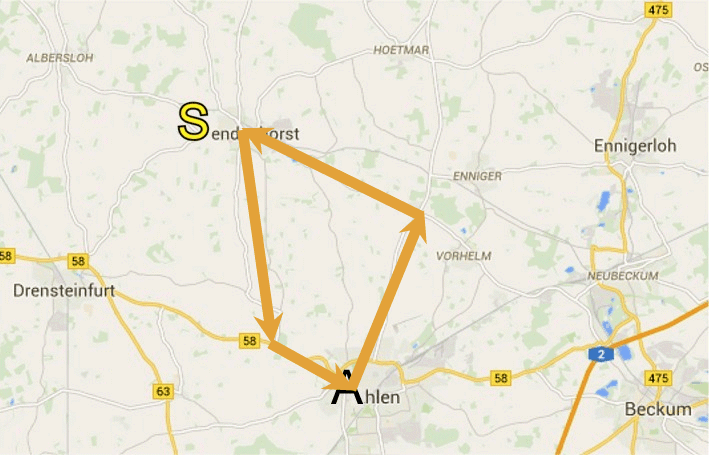
Zur Illustration veranstalten wir einen Rundlauf:vgl. eine Bahnfahrt von Dortmund [B] nach Hamburg [D]: da ist es unerheblich, dass der Zug auch durch Münster [] fährt, aber dort nicht anhält).
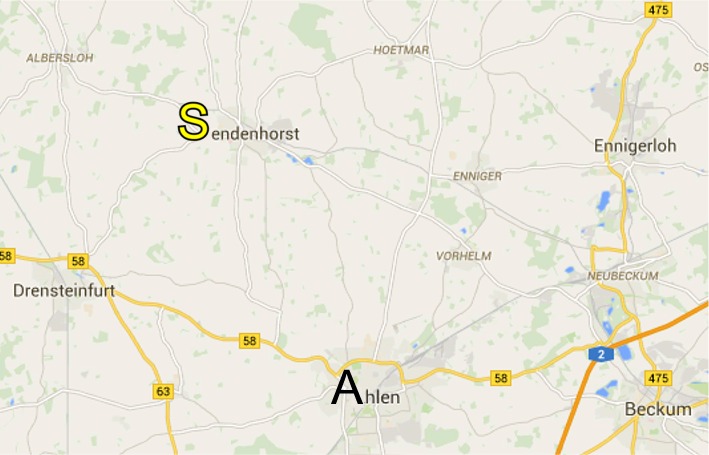 , , |
 ;
;(abgesehen natürlich vom Start = Ziel A)
mindestens ein Zwischenziel
(hier ![]() [endenhost]), und es bleibt
den Läufern überlassen, auf welchen Wegen sie dort hin und
von dort wieder nach A(hlen) zurück kommen
[endenhost]), und es bleibt
den Läufern überlassen, auf welchen Wegen sie dort hin und
von dort wieder nach A(hlen) zurück kommen
(z.B. mag es Läufer geben, die einen Umweg einer Steigung vorziehen);
(der Hallstädtersee ist alles andere als rund:),
sondern erstmal nur, dass man nicht denselben Weg zurück läuft(vektorgeometrisch gesagt [vgl. oben]: die Vektorenden man schon hin gelaufen ist, sondern z.B. inund
sind NICHT KOLLINEAR, d.h. es wird tatsächlich ein Parallelogramm aufgespannt),
(endenhorst) abbiegt
(allerdings bedeutet "Rundlauf" wohl auch [und das ist eine topologische Aussage], dass der Weg sich nicht [wie etwa bei einer 8] selbst kreuzt; bzw. "Rundlauf" bedeutet "um etwas [z.B. einen See] drumherum").
Vorstellbar wäre, dass es in ![]() (endenhorst) einen Kontrollpunkt gibt,
um sicherzustellen, dass alle Teilnehmer des Rundlaufs dort
durchgekommen und nicht einfach in A(hlen) geblieben sind
(endenhorst) einen Kontrollpunkt gibt,
um sicherzustellen, dass alle Teilnehmer des Rundlaufs dort
durchgekommen und nicht einfach in A(hlen) geblieben sind
(was nebenbei ein [wieder mal arg banaler] Fall ist, der unten noch hochinteressant wird).
 |
aber wir gehen natürlich aus purer Faulheit den
(auch rechnerisch)
einfachsten "Rundlauf":
(A)
Alle Vektoren unseres gewählten
Rundlaufs liegen auf den bereits bekannten Vektoren![]() ,
,
![]() ,
,
![]() und
und ![]() und sind deshalb durch diese darstellbar:
und sind deshalb durch diese darstellbar:
| (I) | 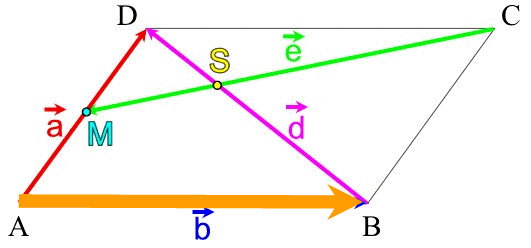 |
|
| (II) |
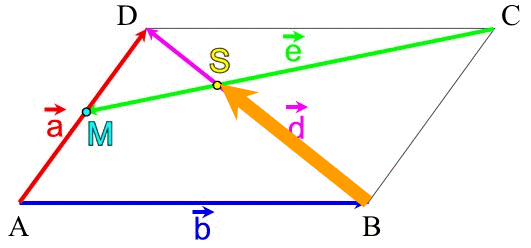 |
Der
Vektor
|
| (III) |
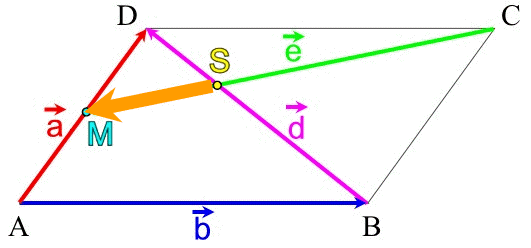 |
Der
Vektor
|
| (IV) |
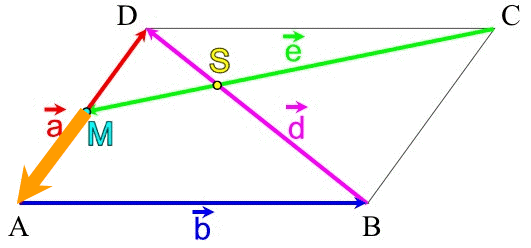 |
Da
- wie von Anfang an festgelegt -
(Das Minus rührt daher, dass |
Bevor wir gleich nur noch rechnen, halten wir nochmal sehr deutlich fest, was die neu eingeführten Unbekannten x und y bedeuten
(wir werden unten darauf zurückkommen)
:
|
 |
|
 |
Wenn man all die soeben hergeleiteten Ergebnisse in unsere Gleichung
(A)
einsetzt, erhält man
(B)
(Spätestens hier ist wohl alle Anschauung am Parallelogramm futsch und liegt nur noch eine reine Rechnung vor. Genau das ist aber typisch für die Lösung aller Textaufgaben:
Es ist also, als wenn man zwischendurch einige Zeit in die Mathematik abtaucht:

In der rein innermathematischen Zwischenphase geht es oftmals nicht mehr ums Verstehen, sondern "nur" darum, richtig und zielgerichtet [???] zu rechnen.
Nebenbei: man muss sich diese unbeabsichtigte Alliteration doch mal auf der Zunge zergehen lassen:
RICHtig
zielgeRICHtet
RECHnen)
(Nebenbei: umständlichere Rundläufe führen letztlich alle zu derselben Gleichungen, da sich bei ihnen Umwege gegenseitig aufheben.)In
|
|
 |
(Das Minus rührt daher, dass
|
|
|
 |
Wenn wir nun diese beiden Darstellungsformen für
![]() und
und
![]() in
in
(B)
einsetzen, erhalten wir
(C)
Damit ist etwas geschehen, was häufig in der Mathematik passiert:
(was ja zwischenzeitlich unser Ziel war)
nur noch die zwei Basisvektoren
![]() und
und ![]() vorkommen.
vorkommen.
(Es ist in der Mathematik wie im "richtigen" Leben: man kann nicht alles auf einmal haben bzw. sich nicht immer nur die Rosinen rausklauben;
in der Mathematik hat man z.B. oftmals nur die Wahl:
Eben war schon gesagt worden, dass die Klammern die Gleichung (C) "schwierig" machen. Dann ist es nur folgerichtig, diese Klammern erstmal zu beseitigen:
(C)
![]() + x •
(
+ x •
( ![]() -
- ![]() ) + y •
( -
) + y •
( -
![]() -
-
![]()
![]() )
-
)
-
![]()
![]() =
=
![]()
(D)
![]() + x •
+ x •
![]() -
x •
-
x •![]() - y •
- y •
![]() -
-
![]() y
y![]() -
-
![]()
![]() =
=
![]()
Oben war so mir nichts, dir nichts von "zielgerichtetem" Rechnen im
innermathematischen Zwischenteil gefaselt worden. Fragt sich nur, was jetzt
unser Ziel sein soll.
Durch Additionen bzw. Subtraktionen sorgen wir nun dafür, dass alle Terme,
in denen ein ![]() enthalten ist, auf die rechte Gleichungsseite kommen
enthalten ist, auf die rechte Gleichungsseite kommen
(auf der linken Gleichungsseite also nur diejenigen Terme bleiben, die ein
erhalten):
(D)+ x •
- x •
- y •
-
y
-
=
| -
+ x •
+ y •

(E) x •-
y
-
= -
+ x •
+ y •

Nun kommt tatsächlich
vor, was bedeutet:
ausklammern:
(E) x •-
y
-
= -
+ x •
+ y •

(F) ( x -y -
) •
= ( -1 + x + y ) •

(Ein bisschen durchgeknallt ist es ja schon, dass wir erst [wohlgemerkt zwecks Vereinfachung!] Klammern beseitigt haben - und jetzt doch wieder welche hinzufügen.)
Diese Gleichung (F)
ist zwar auch
noch nicht sonderlich einfach, weist aber eine schöne (Fast-)Symmetrie
auf:

Vor allem dürfen wir uns aber nicht durch die beiden noch immer
scheußlichen Klammern täuschen lassen:
(G)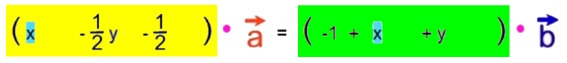
Nun überlegen wir, unter welchen Umständen ein Vielfaches
von ![]() überhaupt gleich einem Vielfachen
von
überhaupt gleich einem Vielfachen
von
![]() sein kann.
sein kann.
Dabei müssen wir berücksichtigen, was wir schon anfangs überlegt hatten
:(und dazu wieder kurz aus der reinen Mathematik auftauchen)
ein (echtes) Parallelogramm kommt überhaupt nur unter zwei Bedingungen
zustande:
Zeichnen wir uns das noch einmal auf:
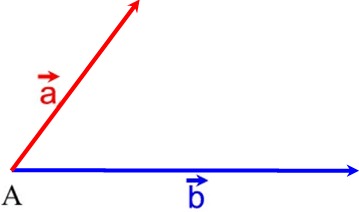
Nun stellen wir uns vor, Arno und Berta starten beide in A und
Wann treffen sie sich?
Otto Normalverbraucher würde da wohl antworten, dass
Arno und Berta
sich niemals treffen, weil sie ja in unterschiedliche
Richtungen gehen.
Mathematiker hingegen antworten arg spitzfindig:
Arno und
Berta treffen sich sehr wohl, aber nur
dann, wenn beide in A bleiben, wenn also
Auf unser Parallelogramm-Problem übertragen heißt das:
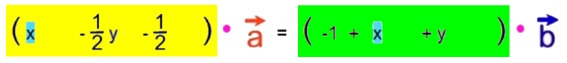
ist nur möglich, wenn
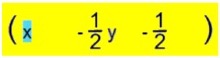 = 0
= 0 = 0.
= 0.Wir haben also aus der einen Gleichung
(G)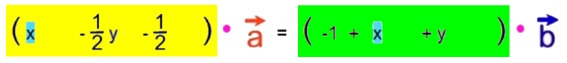
die
beiden Gleichungen
(H)
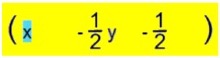 = 0 und
= 0 und
 = 0
= 0
gewonnen und damit auf den ersten Blick alles nur
doppelt so schwer gemacht,
denn jetzt müssen wir ja zwei Gleichungen lösen. Dafür haben aber die
beiden Gleichungen (H)
einen enormen Vorteil: in ihnen kommen
keine Vektoren mehr vor, d.h. mit den
beiden Gleichungen (H)
sind wir
urplötzlich in der hundsgewöhnlichen Algebra der Mittelstufe
gelandet
("nichts Neues unter der Sonne").
Zu lösen ist also das Gleichungssystem
|
|
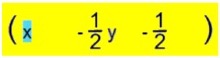 = 0
= 0 |
|
 = 0
= 0 |
| unsere Ergebnisse für x und
y (die wir ja noch nichtmal ausgerechnet haben) werden
gelten!!! |
Unser Gleichungssystem nun ohne die beiden bei der weiteren Rechnung nur ablenkenden Farben grün und gelb:
|
|
x
-
|
|
| -1 + x + y = 0. | +1 - y |
|
|
|
x
-
|
x
= 1 -
y
**
 |
|
|
|
1 - y -
|
| x = 1 - y |
|
|
|
|
| x = 1 - y |
|
|
|
|
| x = 1 - y |
|
|
|
|
| x = 1 - y |
|
|
|
|
| x = 1 - y |
|
|
|
|
|
x
= 1 -
|
|
|
|
|
|
x
=
|
Erstaunlich und vielleicht auch ein wenig ernüchternd ist es ja schon,
dass nach all unseren ellenlangen Ãœberlegungen und Rechnungen jetzt einfach
nur x =
![]() und y =
und y =
![]() herauskommen!
herauskommen!
Und es wird sogar, wie wir gleich sehen werden, noch einfacher.
Ein typisches Problem bei Textaufgaben ist aber: nachdem man ellenlang in die reine Mathematik abgetaucht ist und dort sogar hübsche Ergebnisse erhalten hat, weiß man gar nicht mehr, was diese Ergebnisse im ursprünglichen Aufgabenzusammenhang bedeutet haben.
Erinnern wir uns daher jetzt, wo wir wieder aus der reinen Mathematik auftauchen

daran, was wir oben vorsorglich ganz besonders deutlich aufgeschrieben hatten:
|
 |
|
 |
Damit können wir nun festhalten:
Nun war aber in der ursprünglichen Aufgabenstellung nach dem (=
Singular!) Verhältnis
gefragt, in dem die Strecken
d bzw. e
in ![]() geteilt werden
geteilt werden
(wobei ja [das sei nochmals erwähnt] durch den Singular schon unterstellt wird, dass die beiden Strecken d und e im selben Verhältnis geteilt werden).
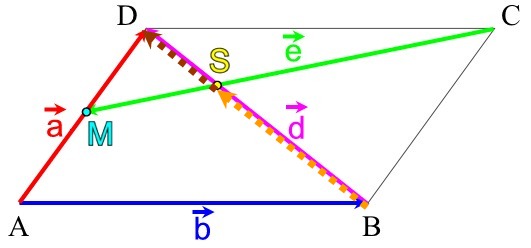
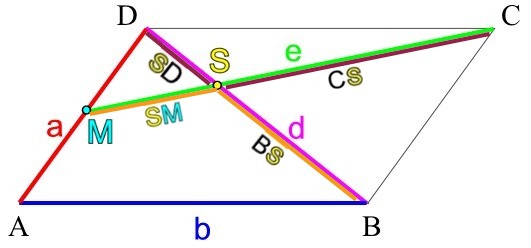
Um die Verhältnisse herauszubekommen, rechnen wir:
|
 |
|
 |
Daraus folgt:
(oder genauer: ihre Längen)
verhalten sich zueinander wie
![]() :
: ![]() = 1 : 2,
= 1 : 2,
(oder genauer: ihre Längen)
verhalten sich zueinander wie
:
= 1 : 2.
| Damit ist endlich (!) bewiesen, dass in allen Parallelogrammen
die beiden Strecken d und
e durch |
Oder anders und einfacher gesagt:
|
 |
Fassen wir die groben Züge unseres Beweises zusammen:
Dass sich in allen Parallelogrammen die Strecken
d und e im
selben Verhältnis
![]() schneiden, finde ich schon erstaunlich genug.
Noch viel erstaunlicher finde ich aber:
schneiden, finde ich schon erstaunlich genug.
Noch viel erstaunlicher finde ich aber:
wenn
![]() bei
bei
![]() von a liegt, werden die Strecken
d und e bei
von a liegt, werden die Strecken
d und e bei
![]() im Verhältnis
1:2
bzw
im Verhältnis
1:2
bzw
![]() geteilt!
geteilt!
Ist das purer Zufall - oder zieht sich
![]() dominant durch die ganze ellenlange Rechnung hindurch?
dominant durch die ganze ellenlange Rechnung hindurch?
Andererseits würde mich Letzteres doch auch nicht ganz
wundern, denn immerhin ist
![]() doch die zentrale Vorgabe der Aufgabe. Erstaunlich finde ich aber, dass es
so unversehrt durch die Rechnungen rutscht, als wäre es
imprägniert.
doch die zentrale Vorgabe der Aufgabe. Erstaunlich finde ich aber, dass es
so unversehrt durch die Rechnungen rutscht, als wäre es
imprägniert.
Wenn
![]() sich aber so brachial durch alle Gleichungen durchschlängelt, würde das dann
auch für
sich aber so brachial durch alle Gleichungen durchschlängelt, würde das dann
auch für
![]() funktionieren?:
funktionieren?:
(... wobei wir den Namen
![]() beigehalten, obwohl
beigehalten, obwohl
![]() nicht mehr
nicht mehr
![]() ittelpunkt
der Strecke a ist)
ittelpunkt
der Strecke a ist)
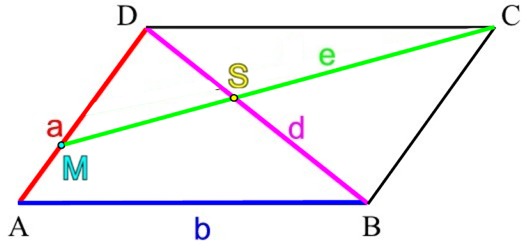
Und dann ergäbe sich für einen Mathematiker sofort ein ganzer Wasserfall von Fragen:
(... wobei vorerst 0 < p < 1; aber was mag es bedeuten, wenn p außerhalb diese Intervals liegt, und gilt dann auch die Vermutung, dass die Strecken d und e im Verhältnis p geteilt werden?)
Die Reihenfolge dieser Fragen muss man wohl erklären:
wenn's laut a. für
![]() funktioniert, möchten Mathematiker es auch für größere Nenner,
also für
funktioniert, möchten Mathematiker es auch für größere Nenner,
also für
![]() in b.,
in b.,
![]() in c.,
in c.,
![]() usw. wissen;
usw. wissen;
(z.B. p =
![]()
![]() 0,707106781)
0,707106781)
Das alles hört sich nach einer Riesenarbeit an, da ja
anscheinend für jeden Nachweis in b. bis f. jeweils ellenlange Rechnungen
wie oben für
![]() nötig zu sein scheinen.
nötig zu sein scheinen.
Kommt hinzu, dass in d. bis f. jeweils Beweise für unendlich viele Zahlen nötig wären, was ja fast ein Widerspruch in sich ist: wie will man in einem Beweis, der doch per se endlich sein muss, unendlich viele Fälle beweisen???
(Dass die Mathematik in der Lage ist, solch endlich lange Beweise für unendlich viele Fälle zu liefern, ist
- ihr "Alleinstellungsmerkmal", weil sie als einzige Wissenschaft sowas [endgültige Wahrheiten aufstellen] kann,
- somit ihre zentrale Tätigkeit,
- für mich nach wie vor höchst erstaunlich.)
Falls wir tatsächlich all die Fragen b. bis e. beantworten wollen, wird's also Zeit, Abkürzungen zu finden.
Aber wo anfangen - wenn wir nicht stupide nacheinander c. bis e. abarbeiten wollen?
Es gäbe da verschiedene Ansätze:
Letzteres hieße, sich überhaupt nicht mit schnödem Kleinkram
(gar - igitt! - konkreten Zahlen)
abzugeben, sondern sich gleich an den Maximalbeweis zu
setzen. Das könnte allerdings auch gefährlich sein: mal angenommen,
es zeigt sich, dass sich nicht alle (reellen) Zahlen
p unverändert durch alle Rechnungen
durchziehen. Dann übersähe man eventuell, dass sich z.B. immerhin alle
Stammbrüche
![]() unverändert durch sämtliche Rechnungen durchziehen.
unverändert durch sämtliche Rechnungen durchziehen.
(Ein hardcore-Maximal-Mathematiker würde da vielleicht sagen: was interessieren mich Behauptungen, die nicht absolut allgemein beweisbar sind?!
Dann dürfte ihn allerdings beispielsweise auch nicht der "Satz des Pythagoras" interessieren, da der ja auch "nur" für rechtwinklige Dreiecke, aber eben nicht für alle [auch nicht-rechtwinklige] Dreiecke gilt.)
Ich möchte hier allerdings einen anderen Weg gehen:
.(wobei natürlich 1 herauskäme; dieser 1 könnte man aber nicht mehr ansehen, wie sie aus
entstanden ist)
Fangen wir also nochmal mit

an:
zuerst ergibt sich wie oben
a.
![]()
b.
![]() =
x •
=
x •
![]()
c.
![]() = y •
= y •
![]()
d. ![]() = -
= -
![]()
![]()
(A)
Wenn wir nun a. bis d. darin einsetzen, ergibt sich wieder
(B)
Wenn wir nun wieder alle Vektoren durch die
Basisvektoren
![]() und
und
![]() ersetzen, erhalten wir wieder
ersetzen, erhalten wir wieder
e. ![]() =
= ![]() -
- ![]()
f. ![]() = -
= -
![]() -
-
![]()
![]()
Genau an dieser Stelle wird's aber gefährlich, was
man vielleicht erst sieht, wenn man (kurz) den Fall
![]() betrachtet:
betrachtet:
schauen wir uns da mal genau an, wie ![]() dann durch
dann durch ![]() und
und
![]() darstellbar ist:
darstellbar ist:
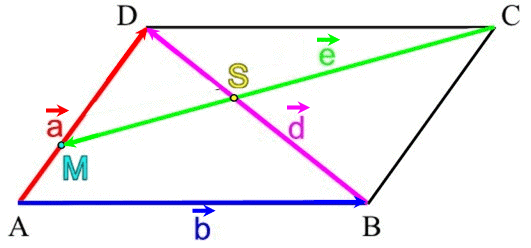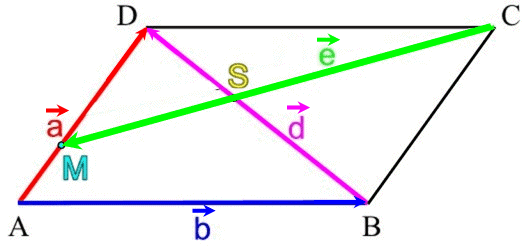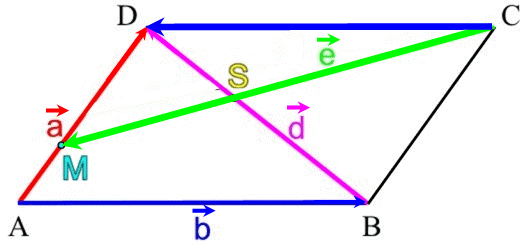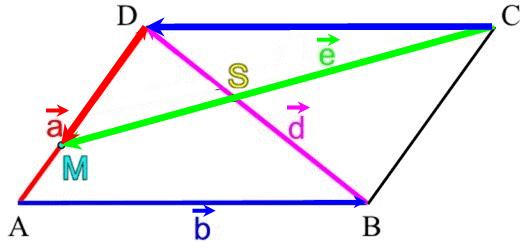
Für den benötigten Vektor
![]() gilt:
gilt:
![]() =
-
=
- ![]()
![]()
Nun wollen wir aber doch alles durch
![]() und nicht etwa durch
und nicht etwa durch
![]() ausdrücken und müssen deshalb erstmal
ausdrücken und müssen deshalb erstmal
![]() = 1 -
= 1 -
![]() schreiben
und damit:
schreiben
und damit:
![]() =
- (1 -
=
- (1 -
![]() )
)![]()
Und entsprechend müssen wir beim Fall
![]() schreiben:
schreiben:
![]() =
- (1 -
=
- (1 -
![]() )
)![]() ,
,
womit sich für ![]() nun ergibt:
nun ergibt:
g. ![]() = -
= -
![]() -
( 1-
-
( 1-
![]() )
)![]()
f. und g. in
(B)
eingesetzt führt dann zu
(C)
Jetzt beseitigen wir wie oben die Klammern:
(C)
.
![]() +
x •
+
x •
![]() -
x •
-
x •![]() + y •
(-
+ y •
(-
![]() - (
- (![]() -
-
![]()
![]() )
-
)
-
![]()
![]() =
=
![]()
![]() +
x •
+
x •
![]() -
x •
-
x •![]() + y •
(-
+ y •
(-
![]() -
- ![]() +
+
![]()
![]() )
-
)
-
![]()
![]() =
=
![]()
(D)
Nun sorgen wir wie oben dafür, dass alle
Summanden, die
![]() enthalten, auf die rechte Seite der Gleichung kommen
enthalten, auf die rechte Seite der Gleichung kommen
(und alle Summanden, die ![]() enthalten, auf der linken Seite der Gleichung bleiben):
enthalten, auf der linken Seite der Gleichung bleiben):
(D)
.
x •
![]() .
- y •
.
- y • ![]() +y •
+y •
![]()
![]() -
-
![]()
![]() = -
= -![]() +
x •
+
x •![]() + y •
+ y •
![]()
oder enger zusammen geschrieben
(E)
x •Da in allen Summanden links
![]() und in allen Summanden rechts
und in allen Summanden rechts
![]() vorkommt,
klammern wir links
vorkommt,
klammern wir links
![]() und rechts
und rechts
![]() aus:
aus:
(F)
( x - y + y •Daraus schließen wir wie oben: (F) ist nur möglich, wenn
(G)
x - y + y •Damit sind wir wieder bei einem Gleichungssystem:
|
|
x - y
+ y •
|
|
| - 1 + x + y = 0 | + 1 - y |
|
|
|
x - y
+ y •
|
x = 1 -
y
 |
Die Umformungen dieses Gleichungssystems seien
hier nicht nochmals detailliert vorgerechnet, sondern ich
behaupte einfach mal, dass dabei x =
![]() und y =
und y =
![]() herauskommen. Und als Teilungsverhältnis erhalten wir
(urplötzlich wieder sehr einfach) 1 -
herauskommen. Und als Teilungsverhältnis erhalten wir
(urplötzlich wieder sehr einfach) 1 -
![]() .
.
Wenn wir das all das nun doch mal vollständig
ausrechnen, erhalten wir wie oben x =
![]() und y =
und y =
![]() und damit das Teilungsverhältnis 1 : 2 bzw.
und damit das Teilungsverhältnis 1 : 2 bzw.
![]() .
.
So weit, so gut. Nur geht leider alles sofort schief,
wenn wir statt
![]() nun
nun ![]() einsetzen: wir erhalten dann als Teilungsverhältnis 1 -
einsetzen: wir erhalten dann als Teilungsverhältnis 1 -
![]() , und wenn wir das ausrechnen, ergibt sich
, und wenn wir das ausrechnen, ergibt sich
![]() und nicht, wie oben in b. erwartet,
und nicht, wie oben in b. erwartet,
![]() .
.
Wir waren vor lauter Abstraktion wohl betriebsblind: dass
![]() nicht stimmen konnte, hätten wir doch schon an der Zeichnung
nicht stimmen konnte, hätten wir doch schon an der Zeichnung

sehen können!
Mit dem Fall b. sind aber auch die Fälle c. bis f. hinfällig: was für eine verlorene Liebesmüh'!
Aber wir wollen versuchen, aus den Trümmern unserer ursprünglichen Vermutungen doch noch was zu machen:
 ,
,
 :
: immerhin hatten wir ja
für den
Fall a., dass
![]() bei
bei
![]() a liegt, das
Teilungsverhältnis
a liegt, das
Teilungsverhältnis
![]()
erhalten und können daher die hoffentlich besseren Vermutungen aufstellen:
im Fall c. wenn also
![]() bei
bei
![]() a liegt, ist das Teilungsverhältnis
a liegt, ist das Teilungsverhältnis
![]() ,
,
Mehr noch: wir können jetzt sogar den "Maximalfall" f.
angehen, wenn also
![]() bei p •
a liegt
bei p •
a liegt
(wobei p reel ist, also sogar eine irrationale Zahl sein kann).
Dazu ersetzen wir in 1 -
![]() den Bruch
den Bruch
![]() einfach durch p und erhalten das zugehörige
Teilungsverhältnis 1 - p.
einfach durch p und erhalten das zugehörige
Teilungsverhältnis 1 - p.
Halten wir also fest:
|
wenn
bei p • a liegt, teilt der Punkt |
Wohlgemerkt: das ist jetzt nicht mehr eine Vermutung, sondern bewiesen!
Und damit können wir nun auch unsere soeben aufgestellten Vermutungen beweisen:
im Fall c., wenn
![]() bei
bei
![]() a liegt, ist das Teilungsverhältnis 1 -
a liegt, ist das Teilungsverhältnis 1 -
![]() =
= ![]() -
-
![]() =
=
![]() =
=
![]() ,
,
| "Ich hatte das Gefühl, durch die Oberfläche
der atomaren Erscheinungen hindurch auf einen tief darunter
liegenden Grund von merkwürdiger innerer Schönheit zu schauen, und
es wurde mir fast schwindlig bei dem Gedanken, daß ich nun dieser
Fülle von mathematischen Strukturen nachgehen sollte, die die Natur
dort unten vor mir ausgebreitet hatte." (Werner Heisenberg) |
Nun möchte ich aber Rechenwege so weit wie möglich verstehen, statt nur darauf zu vertrauen, dass die Rechnungen automatisch richtig sind, und ich möchte, wenn irgend möglich, auch verstehen, warum etwas schiefgelaufen ist.
Fangen wir gleich mit dem "Maximalfall" an: warum hat sich folgende Vermutung als falsch erwiesen?:
: wenn
![]() bei p •
a liegt, teilt der Punkt
bei p •
a liegt, teilt der Punkt
![]() die Strecken d und e
im Verhältnis
p ,
die Strecken d und e
im Verhältnis
p ,
: wenn
![]() bei p •
a liegt, teilt der Punkt
bei p •
a liegt, teilt der Punkt
![]() die Strecken d und e
im Verhältnis
1 - p.
die Strecken d und e
im Verhältnis
1 - p.
Zu A.:
der Fehler ist eingetreten, als
![]() durch
durch ![]() ausgedrückt wurde: allgemein gesprochen, hatten wir die Gleichung
ausgedrückt wurde: allgemein gesprochen, hatten wir die Gleichung
![]() =
- p •
=
- p •
![]() aufgestellt, aber es musste korrekt
aufgestellt, aber es musste korrekt
![]() =
- (1 -
p
)
=
- (1 -
p
)![]() heißen. Da wir anfangs aber mit p =
heißen. Da wir anfangs aber mit p =
![]() gearbeitet hatten und in diesem (einzigen!) Fall tatsächlich 1 -
gearbeitet hatten und in diesem (einzigen!) Fall tatsächlich 1 -
![]() =
=
![]() ist, war uns der kleine notwendige Schlenker 1 - p
gar nicht aufgefallen.
ist, war uns der kleine notwendige Schlenker 1 - p
gar nicht aufgefallen.
Wir hatten also zu früh verallgemeinert:
Und doch war unsere falsche Vermutung f., also
allzu schön und ist die richtige Feststellung
nur noch halb so schön, weil sich da p in 1 - p verwandelt.
Aber das läßt sich immerhin ein wenig nachbessern:
c.: wenn
![]() von D aus gesehen
bei (1- p ) •
a liegt, teilt der Punkt
von D aus gesehen
bei (1- p ) •
a liegt, teilt der Punkt ![]() die Strecken d und e
im Verhältnis
die Strecken d und e
im Verhältnis
durch sämtliche Rechnungen durch.
Zu B.:
Der Versuch, anschaulich zu verstehen, wie sich p bzw. 1 - p durch sämtliche Rechnungen durchzieht, scheint mir aber gescheitert: dazu sind die Rechnungen einfach (!) viel zu umständlich.
Es kann ebenso Nach- wie Vorteile haben, wenn man an einer Mathematikaufgabe sehr lange rumdoktort:
(dann allerdings oft urplötzlich:
 )
)
zu einem Bild
 ,
,
und erst so im Nachhinein sieht man dann einfachere, schon früher vorhandene Möglichkeiten
(es ist, wie wenn man ein Buch / einen Film zum wiederholten Mal liest / anschaut und denkt: "diese frühzeitige Andeutung hätte ich beim ersten Lesen / Anschauen doch nicht überhören dürfen"):
erst spät habe ich die enorme Aussagekraft der so harmlos daherkommenden Gleichung
x = 1 - y

erkannt, also jener Gleichung, die wir in den Gleichungssystemen oben die ganze Zeit unverändert mitgeschleppt hatten, um am Ende, nachdem wir y ausgerechnet hatten, aus diesem auch noch x ausrechnen zu können.
Erst jetzt wird mir klar: wenn wir herausfinden wollen, ob
d und e durch ![]() im selben Verhältnis
geteilt werden, könnte doch die Gleichung
x = 1 - y
der Schlüssel zum Verständnis sein, da diese Gleichung erstaunlich einfach
im selben Verhältnis
geteilt werden, könnte doch die Gleichung
x = 1 - y
der Schlüssel zum Verständnis sein, da diese Gleichung erstaunlich einfach
verknüpft.
Nun erinnert aber 1 - y fatal an 1 - p , also den "anderen Anteil" der Strecke a, wenn p der "eine Anteil" der Strecke a ist:
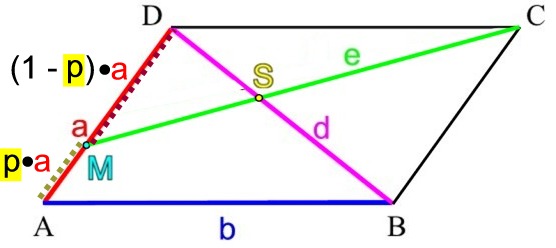
Als mir das
(nach obiger langer Beschäftigung mit dem Wechselspiel von p und1 - p )
klar wurde, blickte ich urplötzlich auf den "Grund" der Gleichung x = 1 - y und erkannte ich ohne jede weitere Rechnung, was ich im Folgenden allerdings nur mit einem Batzen weiterer Ãœberlegungen und Rechnungen klarmachen kann:
dass mit der Gleichung x = 1 - y nämlich schon ziemlich zu Beginn der Gleichungssystem-Umformungen klar war, was die Aufgabe schon von Anfang suggeriert hatte:
dass die beiden Strecken
d und e durch ![]() im selben Verhältnis
geteilt werden.
im selben Verhältnis
geteilt werden.
Schauen wir uns dazu nochmals an, wie
d und e durch ![]() durch geteilt werden:
durch geteilt werden:

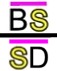 =
= 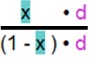 =
=
 =
=
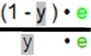 =
=
Nun sehen die Ergebnisse
![]() und
und
![]() zwar schon sehr ähnlich aus, aber es fehlt noch der entscheidende
"Kleber"
x = 1 - y
.
zwar schon sehr ähnlich aus, aber es fehlt noch der entscheidende
"Kleber"
x = 1 - y
.
Wenn wir damit für
x in
![]() nun 1
- y einsetzen, erhalten wir
nun 1
- y einsetzen, erhalten wir
=
,
und damit ist wie von Zauberhand
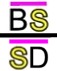 =
=
![]() entstanden, und somit gilt
entstanden, und somit gilt
 =
=
 , womit bewiesen ist, dass die beiden Strecken
d und e durch
, womit bewiesen ist, dass die beiden Strecken
d und e durch ![]() im selben Verhältnis geteilt werden.
im selben Verhältnis geteilt werden.
Nun könnte man denken: dann hätten wir uns ja die weiteren Umformungen der Gleichungssysteme sparen können. Aber Vorsicht!:
(Das erinnert an sogenannte "Existenzbeweise": z.B.
[z.B. eine Lücke von einer Millionen aufeinander folgenden natürlichen Zahlen, von denen keine einzige eine Primzahl ist],
Solche Existenzbeweise finde ich aber doch wahrhaft erstaunlich: es ist, als würde man auf mittelalterliche Weise die Existenz Gottes beweisen, aber damit noch lange nicht wissen [und vielleicht auch nie erfahren], wo zum Teufel er sich versteckt hat.)
Immerhin ist klar: bei unserer Aufgabe steht und fällt alles mit "1 minus irgendwas", was von den Teilungsverhältnissen herrührt (s.o.).
Ich hätte noch in anderer Hinsicht schlauer sein müssen:
wie bei mir üblich, habe ich für die Schüler ein Modell gebaut:

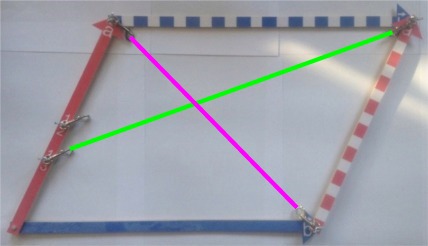

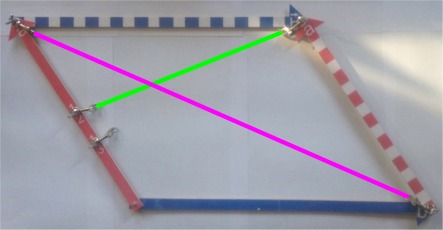


Das sind aber, wenn es um den Allgemeinfall geht, viel zu
wenig Möglichkeiten. Viel besser wäre es, wenn man
![]() auf a bzw.
auf a bzw.![]() kontinuierlich
hin- und herschieben und dabei eindrücklich sehen könnte, wie sich mit
kontinuierlich
hin- und herschieben und dabei eindrücklich sehen könnte, wie sich mit
![]()
Kurz: ich hätte mein Grundprinzip der "bewegten Mathematik" viel ernster nehmen und konsequenter umsetzen müssen.
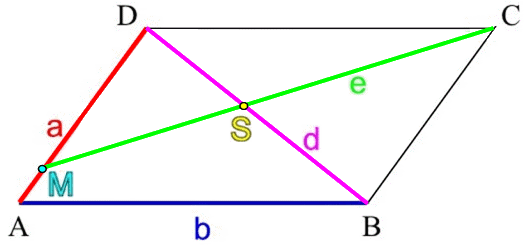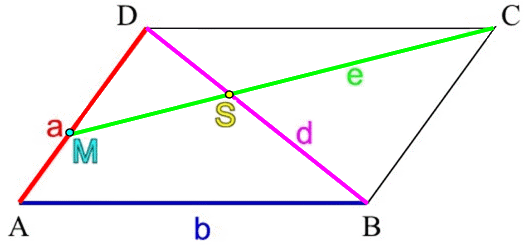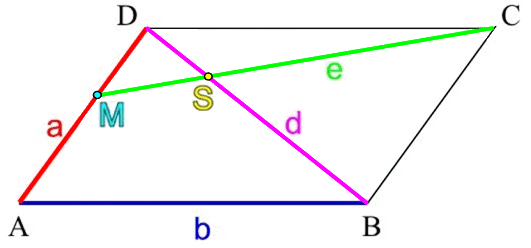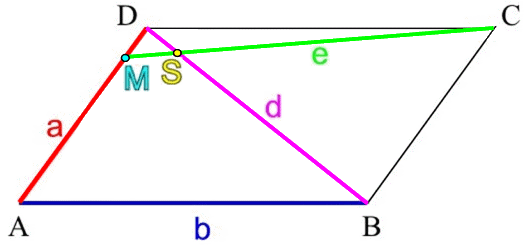
Das Modell ist also demnächst derart umzuarbeiten, dass
![]() kontinuierlich
auf a bzw.
kontinuierlich
auf a bzw.![]() bewegt werden kann:
bewegt werden kann:
(das heißt im obigen Sprachgebrach: je größer p wird),
 ,
,  .
. Interessant daran ist vor allem das "größer / kleiner" oder genauer:
je größer p, desto kleiner die Teilungsverhältnisse.
Allein durch Anschauung ist zwar noch nicht klar, wie genau sich die Teilungsverhältnisse in Abhängigkeit von p verändern, aber das hatten wir ja bereits oben berechnet:
wenn
![]() bei p •
a liegt, teilt der Punkt
bei p •
a liegt, teilt der Punkt
![]() die Strecken d und e
im Verhältnis
1 - p
die Strecken d und e
im Verhältnis
1 - p
Erst jetzt wird (mir) dieses 1 minus irgendwas, das oben als so fundamental für den gesamten Lösungsweg aufgezeigt wurde, wirklich verständlich: es bedeutet
(wie mir - ich muss es zu meiner "Schande" gestehen - erst jetzt klar wird)
schlicht und einfach (ein wenig vereinfacht) "desto kleiner".
Nach all dem Gewimmel wird Karl Mustermann
(der allerdings gar nicht bis hier gelesen hat)
vermutlich "Und was soll der Scheiß?!" fragen, was ja wohl eine rhetorische Frage mit den suggerierten Antworten ist:
(was soll man mit Scheiße schon "anfangen"?!).
Falls Herr Mustermann allerdings unter "anfangen" eine Anwendung versteht, wird's problematisch:
Nun ist die rhetorische Frage "Und was soll der Scheiß?!" aber vielleicht
schon falsch gestellt, denn was "soll" denn z.B.
 oder
oder
 ? Mit beiden kann man doch auch "nichtmal einen Nagel in die Wand schlagen"!
? Mit beiden kann man doch auch "nichtmal einen Nagel in die Wand schlagen"!
(Bei der Mona Lisa
[deren Schönheit sich mir immer entzogen hat]
könnte man immerhin sagen, dass sie enorm viel Geld wert ist - womit wir beim stramm kapitalistischen Verwertungsinteresse wären.)
Wenn nun aber
(zumindest für mich)
keine Anwendung unserer Aufgabe absehbar ist: was dann interessiert oder gar fasziniert "die" Mathematiker an dieser Aufgabe
(oder ähnlichen Aufgaben)?

"Der Versuch, anschaulich zu verstehen, wie sich p bzw. 1 - p durch sämtliche Rechnungen durchzieht, scheint mir aber gescheitert: dazu sind die Rechnungen einfach (!) viel zu umständlich."
Dann scheinen die Parallelogramme, die das Verhältnis 1 - p herstellen, ja sogar noch schlauer als wir oder zumindest ich zu sein!
(G)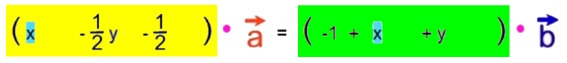
(H)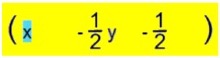 = 0 und
= 0 und
 = 0
= 0
gefolgert werden kann und damit alles von der Vektorgeometrie in die simple Elementaralgebra "abrutscht"
(viel mehr als letztere können Mathematiker eh nicht).