vereinfachen UND diversifizieren

Wenn man lustig ist, kann man den Sinus als "Schattenlänge" eines Stabes definieren, der auf einer sich drehenden Scheibe befestigt ist

(genauer gesagt: als Entfernung des Stabschattens vom Scheibenmittelpunktschatten) .

Vgl. .

Nun erhält man aber je nach Scheibendurchmesser verschieden hohe "Sinusfunktionen":

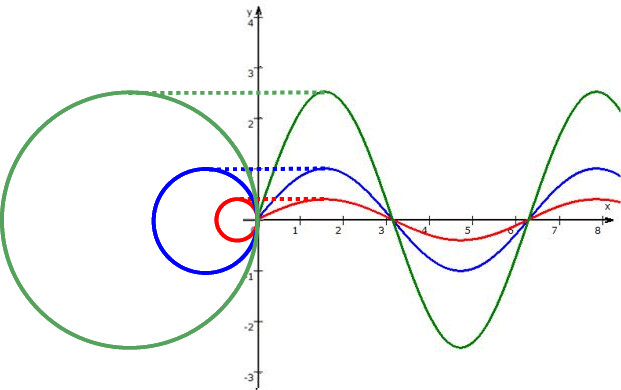
Um solches (erstes) Kuddelmuddel zu vermeiden, nimmt man sich den denkbar einfachsten, also den "Einheitskreis" (mit dem Radius r = 1) und definiert überhaupt erst daran den Sinus:

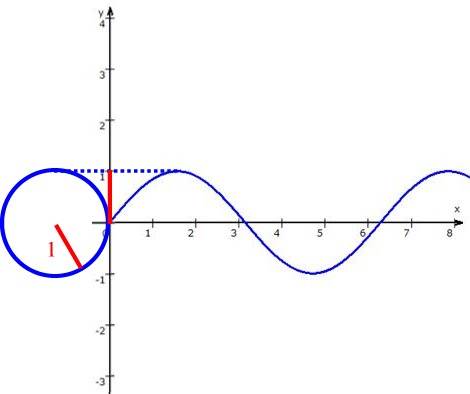
Nun kann der Sinus

(genauer: der Graph der Sinusfunktion) 

allerdings auch verschieden breit ausfallen, je nachdem, wie man den Winkel auf der y-Achse abträgt:

Hier sei nur kurz erwähnt, dass man, um dieses zweite Kuddelmuddel zu vermeiden, vom Winkelmaß

(das im unschönen 90er-System funktioniert)

zum hübsch dezimalen Bogenmaß

(auch am Einheitskreis definiert!) 

übergeht - und erst dann endgültig erhält:

Durch beide Vereinheitlichungen zusammen hat man also folgendes doppelt gemoppeltes Kuddelmuddel vermieden: 

Der Sinus wurde also doppelt in ein Korsett geschnürt

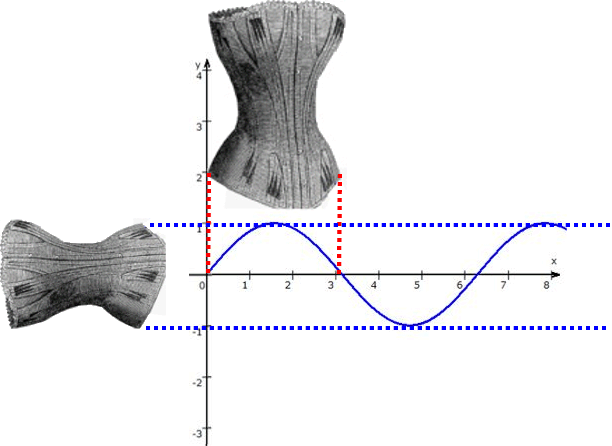
(nebenbei: Sinus [lat.] = Bucht, Busen),

und da könnte man vermuten, dass er dadurch derart eng definiert wurde, dass er nur noch in einsamen Spezialfällen

(beispielsweise nur bei Dreiecken, die mindestens eine Seite der Länge 1 haben) 

brauchbar ist:

es ist alles zwar "schön" einheitlich geworden, aber anscheinend doch auch tot: es erinnert an einen "gepflegten" deutschen Vorgarten oder  

Operation gelungen, Patient tot.

Bislang haben wir uns mit einem der beiden wichtigen Aspekte beim Sinus beschäftigt, nämlich der Sinusfunktion bzw. ihrem Graphen.

Der andere wichtige Aspekt beim Sinus ist hingegen, dass mit ihm spezielle Rechnungen am rechtwinkligen Dreieck möglich werden

(Man kann mit dem Sinus überhaupt erstmals in der Schulzeit Seiten und Winkel eines Dreiecks in Beziehung setzen, während man vorher

• nur mehrere Winkel [Winkelsumme]
• oder nur mehrere Seiten [Satzgruppe des Pythagoras]

in Beziehung setzen und somit auseinander errechnen konnte.

Üblicherweise wird der Sinus gegen Ende der Mittelstufe eingeführt und ist somit deren würdiger Schlussstein  

[was man deutlich hervorheben, ja regelrecht feiern sollte!].

In der Oberstufe kommt dann [zumindest in der Analysis] fast nichts Neues mehr hinzu, sondern wird der Mittelstufenstoff "nur" differenzierter [!] entfaltet.)

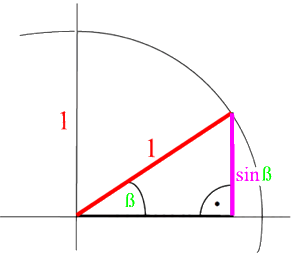
Im Einheitskreis lässt sich sehr leicht der Sinus eines Winkels ß ablesen:

Nehmen wir nun ein beliebiges Dreieck ABC hinzu

(also eines, dass keine Seite der Länge 1 hat),

allerdings wieder ein rechtwinkliges, und legen es intelligent zu unserem Einheitsdreieck:

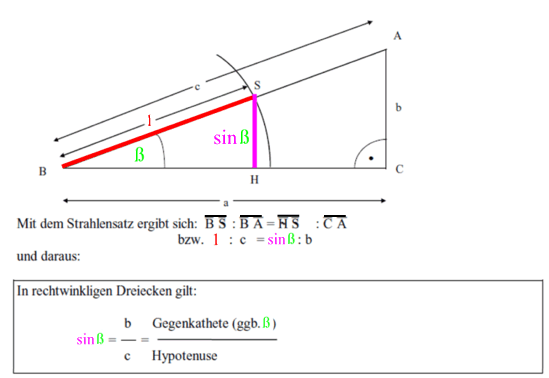
(nebenbei: diese letzte Gleichung
[obwohl sie doch für alle rechtwinkligen Dreiecke gilt]
ist überhaupt erst so besonders einfach, weil wir vorher für die 1 gesorgt hatten)

Wohlgemerkt: diese letzte Gleichung gilt für alle rechtwinkligen Dreiecke d.h. diese letzte Gleichung gilt auch dann, wenn die (rechtwinkligen!) Dreiecke keine Seite mit der Einheitslänge 1 haben!

(Die Rechtwinkligkeit als bleibendes Korsett werden wir also beim Sinus [wie auch beim "Pythagoras"!] leider nicht los.

Woran liegt das?: weil für den Strahlensatz die Strecken HS und AC parallel sein müssen und die Strecke HS nunmal von Anfang an senkrecht auf BH stand.)