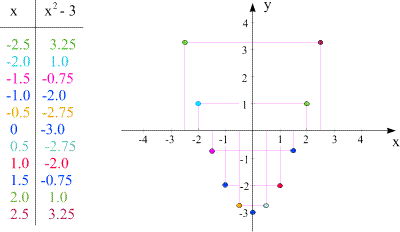
die gute alte Wertetabelle

keine Frage: an einer Wertetabelle allein sieht man kaum etwas,
sondern sie schreit nach der Umsetzung in einen Graphen,
der erst Zusammenhänge verdeutlicht

Meiner Meinung nach werden im üblichen Schulunterricht

• zu viele Standardfunktionen,

• zu viele Funktionsgleichungen ohne Bezug zu den jeweiligen Funktionsgraphen

durchgenommen. Das macht durchaus Sinn:

• erst mal die einfachen, regelmäßigen, nach einem Standardverfahren behandelbaren Funktionen
  (jedeR MathematikerIn weiß, wie schwierig Ableitung und insbesondere Integration bei "Ausreißern" sein können),

• auf die Dauer muss ja in der Tat die Abstraktion von den Graphen erfolgen.

Mir scheint aber, dass vor lauter Standardfunktionen ohne Funktionsgraphen all zu schnell der "funktionale Zusammenhang" abhanden kommt, d.h.

• die "gleitende" Abhängigkeit der y von den x,

• die Beziehung zwischen Funktionsgleichungen und -graphen:

die simple (später ja auch analog in der Vektorrechnung benötigte) "Gleichsetzung"

Geometrie		Algebra
Ein Punkt P (x | y) liegt genau dann auf dem Funktionsgraphen von f		wenn seine beiden Koordinaten x und y die Funktionsgleichung von f erfüllen,

also meiner Meinung nach "der Fundamentalsatz der Funktionenlehre", ist den SchülerInnen nicht mehr präsent (wenn überhaupt jemals geworden), was sich z.B. auch darin ausdrückt, dass

• ein Nullpunkt des Graphen für sie nicht mehr

  • N     (x |   0)
  • und f(x) = 0
• und ein Schnittpunkt mit der y-Achse nicht mehr
  • S_y    (0 |    y )
  • und f(0) = y

bedeutet (!), ihnen also sogar die simpelsten "Haltepunkte" eines Funktionsgraphen fehlen und sie sich somit an gar nichts mehr "festhalten" können.

Mehr noch: das Konstruktionsprinzip des Koordinatensystems, d.h.  kommt ihnen abhanden.

Heutzutage gibt es "Funktionenplotter"-Programme, in die man "vorne" die Funktionsgleichung eingibt, worauf dann "hinten" der zugehörige Graph "heraus" kommt. Zweifelsohne machen solche Programme Sinn, um Grundeigenschaften verschiedener Funktionenklassen zu untersuchen und an verschiedenen Parametern zu "drehen". Vor allem ist es aber (insbesondere bei komplexeren Funktionen) auf die Dauer viel zu mühsam und zeitraubend, immer erst Wertetabellen und daraus dann die Funktionsgraphen zu erstellen.

Mehr noch: auf die Dauer sollen die SchülerInnen ja z.B. internalisiert haben: die Graphen quadratischer Funktionen der Form f: y = ax² + bx + c

• sind immer parabelförmig,

• und um sie zu zeichnen, brauche ich "nur" den Scheitelpunkt S, von dem aus ich dann

  • 1 nach links und a nach oben bzw. unten

  • und 1 nach rechts und ebenfalls a nach oben bzw. unten gehe:

Solch allgemeine ("invariante") Eigenschaften sind ja gerade der Gag, und da wäre die nochmalige Anfertigung einer Wertetabelle und daraus des Funktionsgraphen natürlich nur ein Rückfall (vom Allgemeinen zurück zum Spezialfall).

Ein Funktionenplotter sollte also inzwischen zur Standardausrüstung aller SchülerInnen gehören!

Und doch kommt es da - wie bei allen Computerprogrammen - auf den richtigen Zeitpunkt des Einsatzes an:

Computerprogramme werden oft zu pauschal und zu früh eingesetzt: sie verbergen zentral wichtige Erkenntnisse, weil sie sie schon (in ihrer uneinsehbaren Programmierung) implizieren:

ein Funktionenplotter verbirgt eben

• die Wertetabelle, aus der der Graph überhaupt erst entsteht
  (also den "funktionalen Zusammenhang"),

• die "Übersetzung" der Wertetabelle in den Graphen:

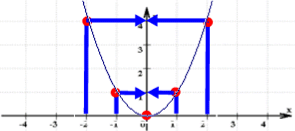
Wir werden - das sei schon vorweg gesagt - unten noch sehen, dass Funktionenplotter noch andere Nachteile haben:

• tatsächlich falsche oder zumindest doch unvollständige Graphen anzeigen,

• weitere mathematische Erkenntnisse wie z.B. "hebbare Polstellen" verbergen.

Die Standardfunktionen (insbesondere die quadratischen) haben den massiven Nachteil, dass sie den SchülerInnen schon allzu selbstverständlich sind

(was ja überhaupt oftmals ein Problem im Mathematikunterricht ist: die SchülerInnen kennen schon "woanders" her [aus dem Physikunterricht, Formelsammlungen ...] die doch eigentlich erst zu erarbeitenden Ergebnisse, und deshalb ist jede "Luft", d.h. jede Motivation, einer Formel selbst auf die Schliche zu kommen, heraus):

beispielsweise die Parabel (ihre Entstehung) lässt sich schon allein deshalb nicht mehr "problematisieren", weil sie den SchülerInnen oftmals vorweg bekannt ist, nämlich z.B., wenn sie bereits eine Parabelschablone besitzen:

(und auf dieser Schablone sind dann gleich auch noch andere Standardgraphen mitgeliefert)

Um dieser Selbstverständlichkeit zu entkommen, wird einE "guteR" LehrerIn natürlich möglichst schnell auf gestreckte oder gestauchte Parabeln ausweichen, bei denen die Parabelschablone nicht mehr zu gebrauchen ist. Und dennoch ist mit der Parabelschablone allzu eindeutig die (gegebenenfalls zu streckende oder zu stauchende) Grundform vorgegeben: so eindeutig, damit aber auch unreflektiert, dass SchülerInnen, wenn sie dann mal selbst eine Parabel zeichnen sollen, oftmals z.B. Folgendes zeichnen (Originalgraph eines Schülers):

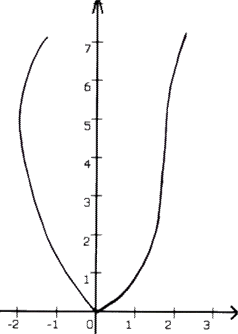
Solch ein Graph beweist aber, dass wirklich Grundlegendes vor lauter Suggestivität nicht verstanden wurde:

• fehlende Symmetrie,

• eine "Ecke" (Nicht-Differenzierbarkeit) im Ursprung,

• (im 1. Quadranten) keine durchgehende Linkskurve (und [fast] senkrecht?),

• vor allem aber: (im 2. Quadranten) nicht mal ein Funktionsgraph.

(Wenn sowas in einer Nachprüfung passiert,

• ist man fast versucht, die Prüfung abzubrechen oder zumindest genauer nachzufragen
  [nochmals wieder bei Adam & Eva anzufangen],

• fragt man sich ja doch, wie schlecht denn eigentlich der eigene Unterricht war, dass "die" SchülerInnen nicht mal "sowas" können.)

Mir scheint also, dass überhaupt erst (wieder) an ganz ungewöhnlichen Funktionen klar wird, wie der "funktionale Zusammenhang" funktioniert (!) und im Koordinatensystem sichtbar wird.

Gerade an diesen ungewöhnlichen Funktionen zeigt sich oftmals, dass die SchülerInnen ohne feste Raster (eben für Standardfunktionen) völlig hilflos sind, nämlich keinerlei Vorstellung vom Funktions(graphen)verlauf entwickeln können.

Zudem wird unten noch deutlich werden, wie man anhand

• ungewöhnlicher,

• aber doch nicht völlig irregulärer,

• sondern zusammengesetzter Funktionen

durchaus viel

• über Standardfunktionen

lernen bzw. wiederholen und festigen kann.

Bevor wir zur Betrachtung zweier spezieller Funktionen kommen, sei noch kurz auf das Problem zu sprechen gekommen, wo man eine Wertetabelle überhaupt "ansiedeln" sollte.

Da es MathematikerInneN "ums Prinzip" geht, verwenden Sie zwar gerne unterschiedliche Koeffizienten

(die dann beispielsweise eine Streckung, Stauchung, Spiegelung oder Verschiebung bewirken),

aber doch gerne einfache , also kleine ganze Zahlen.

• die Koeffizienten kommen also oftmals kaum über + 10 und unter -10 hinaus, und deshalb ist es oftmals sinnvoll, Wertetabellen für diesen Bereich (und zudem nur für ganze Zahlen) anzulegen;

• besonders einfach zu rechnen ist mit x = 0, x = 1 oder x = -1

(wobei man zudem oft besonders markante Werte erhält:

• für x = 0 eventuell den Schnittpunkt mit der y-Achse,

• für x = 1 Grundelemente der Funktion
  [Steigungsdreieck, Koeffizient vor dem x mit dem höchsten und bestimmenden Exponenten]);

x = 0, x = 1 und x = -1 sollten also immer in einer Wertetabelle vorkommen;

• viele Funktionen sind (wenn auch nicht unbedingt zur y-Achse) symmetrisch, und deshalb empfiehlt es sich, "um Null herum" symmetrische x-Werte zu wählen, also z.B. x = 5 und x = - 5;

• eine feinere Einteilung (als ganze Zahlen) ist um besondere Punkte herum sinnvoll

(wenn man sie - etwa aufgrund der erkannten Funktionenklasse - überhaupt schon "sieht" bzw. ahnt):

• Minima, Maxima,

• Stellen, an denen durch 0 geteilt würde
  (die x, bei denen das passieren würde, müssen natürlich von Anfang an aus dem Definitionsbereich ausgenommen werden, ja nach solchen Stellen sollte man wohl als allererstes suchen;
  ein zweiter Blick sollte immer der [falls überhaupt bekannt] Grundeigenschaft einer Funktion gelten:

  • Potenz- oder Exponentialfunktion?

  • quadratisch [d.h. höchster Exponent = 2]?);

• bei eventuell asymptotischen Funktionen lohnt es sich zudem, (symmetrisch) sehr große Wert zu wählen, also z.B. x = 100 und x = - 100.

Als Beispiele ungewöhnlicher Funktionen

(die durchaus behandelt werden können, wenn Ableitung und Integration noch gar nicht bekannt sind; vgl. Orientierungslauf "Grundwissen über Funktionen")

seien hier genommen:

• f: y =

• g: y =

(diese beiden Funktionen wurden gewählt, weil

• daran - wie unten noch gezeigt wird - besonders interessante und wichtige Effekte entdeckt werden können,

• wohl selbst ausgefuchste MathematikerInnen nicht auf Anhieb "sehen" werden, wie die Funktionsgraphen aussehen bzw. die Funktionen sich verhalten - was doch überhaupt erst eine [wenn auch natürlich rein innermathematische] Motivation schafft, sich ihnen langsam anzunähern).

Zu f: y =

Die Funktion lässt sich zusammensetzen aus

• p: y = 4 ^x     (Exponentialfunktion)

• q: y = ¹/_x     (Hyperbelfunktion)

• r: y = sin (x) (Sinusfunktion)

Abgesehen von den oben genannten Standardwerten ergeben sich damit als ebenso interessante wie kritische Stellen in der Wertetabelle:

• Exponentialfunktion p:

  • keine Nullstelle,

  • asymptotisch gegen die x-Achse, also Wahl eines sehr "großen" x (s.o.),

  • besonders einfache Werte ergeben sich für 4¹ = 4 und 4⁰ = 1;

  • Folgefragen:

    • wann wird ¹/_x = 1? (für x = 1)

    • wann wird sin(x) = 1? (für 1 ● /₂, 5 ● /₂, 9 ● /₂ ...)

    • wann wird ¹/_x = 0? (nie!)

• Hyperbelfunktion q: für x = 0 nicht definiert!

  • Folgefrage: wann wird der Nenner sin(x) = 0? Nämlich für x = n ● ; hier ist wieder asymptotisches Verhalten erwartbar (und zwar - da wird noch drauf zurück zu kommen sein - "oben" und "unten"!), und deshalb sollten für die Wertetabelle mal x-Werte ganz in der Nähe solch einer Stelle, also z.B. in der Nähe von 0 ● = 0 und 1 ● = ausgewählt werden;

• Sinusfunktion r: markante Werte für x = m ● /₂ (da sind die Werte 0 sowie 1  oder -1), d.h. auch einige dieser Stellen (für kleine m) sollten mal in die Wertetabelle eingesetzt werden.

Viel weiter wird man wohl kaum kommen - und braucht man auch gar nicht zu kommen (ja nicht mal zu rechnen!): man ist vorgewarnt, was an bestimmten Stellen passieren könnte - und kann jetzt (jetzt erst!) tatsächlich zum Funktionenplotter greifen:

Zwar konnte wohl niemand den genauen Graphenverlauf vorausahnen, aber immerhin besttätigen sich viele der oben angestellten Vermutungen für Wertetabelle.

Dennoch ergeben sich aber auch berechtigte Zweifel

(die man nie bemerkt hätte, wenn man ohne Vorüberlegungen gleich den Funktionenplotter benutzt hätte):

• Die Funktion scheint eben doch Nullstellen zu haben (z.B. in N), was aber nach o.g. Überlegungen ausgeschlossen war.

• Was passiert eigentlich beispielsweise auf dem rot markierten Bereich, wo die Funktion ja durchaus definiert ist, der Funktionenplotter aber nichts anzeigt?

Um beides genauer zu untersuchen, nutzen wir für den grün umrandeten Bereich die Zoomfunktion des Funktionenplotters und erhalten (aber nur aufgrund der Vorüberlegungen!) ein aussagekräftigeres Bild:

1. scheinen im vorher rot markierten Bereich durchaus noch Werte vorzuliegen,

2. sieht es (wie nach den Vorüberlegungen zu erwarten) so aus, dass dort asymptotisches Verhalten, aber keine Nullstelle vorliegt.

Inzwischen skeptisch gegenüber der Anzeige des Funktionenplotter geworden, spielen wir ein bisschen weiter und verkleinern den Graphen nun. Dabei ergibt sich etwas sehr Merkwürdiges:

Zumindest laut Funktionenplotter enden die Graphen an Stellen (z.B. ● ), wo laut den Vorüberlegungen asymptotisches, also unendliches Verhalten zu erwarten wäre.

Was ist passiert?:

• hat das Programm einen Fehler gemacht?
  (und weshalb?; nun können wir zwar nicht seine innere Programmierung untersuchen, aber es lässt sich ahnen, dass er in der Nähe von Stellen Schwierigkeiten hat, wo durch 0 geteilt würde; dass er also sehr große und sehr kleine Werte nicht anzeigen und vielleicht auch erst gar nicht berechnet)

• oder wird uns hier ein entscheidender Hinweis auf bislang Unerkanntes gegeben? Also z.B. darauf, dass diese Punkte auf dem Graphen einer - es sollte uns nicht erstaunen - Exponentialfunktion liegen?

Inzwischen also misstrauen wir gründlich den Fähigkeiten von Funktionenplottern

(auch wenn sie oftmals durchaus hilfreich sind).

Erst mal misstrauisch geworden, stellt sich also die Frage, ob uns der Funktionenplotter überhaupt annähernd den richtigen Grobverlauf (ganz zu schweigen von den Details) der Funktion angezeigt hat.

(Misstrauen gegenüber Computerergebnissen ist auch ein Lernziel, aber erst nach Vorüberlegungen ohne den Computer möglich!)

Gerade weil der tatsächliche Funktionsgraphenverlauf wohl erst durch den Funktionenplotter klar wird, ergeben sich damit auch Rückfragen, also z.B.:

• auf Anhieb hätte man bei einer Exponentialfunktion eventuell folgenden typischen Verlauf erwartet:

,

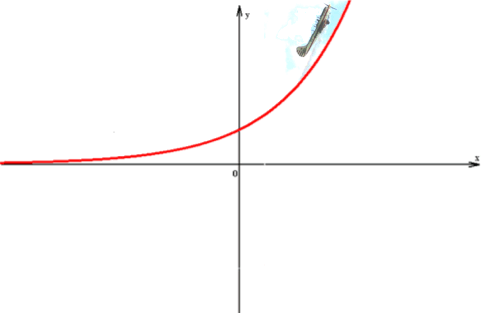also bestimmt nicht die schöne Symmetrie bzw. fast schon Langeweile im Graphen von f: y = , die offensichtlich vom periodischen Sinus her stammt;

• die Rückfrage wäre also: wie geht der Sinus ins Endergebnis ein, d.h. insbesondere:

  • was passiert bei notorischen x-Werten des Sinus mit ,

  • wie geht die Eigenschaft -1 ≤ sin(x) ≤ 1 in ein,

  • wie geht die Periodizität von sin(x) in ein?

Solche Überlegungen scheinen mir viel wichtiger als immer (nur) Rechnungen (an Standardfunktionen).

Zu g: y =

Die Funktion lässt sich ähnlich zusammensetzen wie die vorher genannte. Hier soll daher nur ein Aspekt betrachtet werden:

• für x = 0 ist die Funktion nicht definiert; weil das x im Exponenten aber in einer Hyperbelfunktion auftaucht, ist in der Nähe des x asymptotisches Verhalten zu erwarten.

Der Funktionenplotter zeigt aber

• sehr wohl einen Funktionswert für x = 0

• und in dessen Nähe keinerlei Asymptotik

an:

Inzwischen skeptisch gegenüber Funktionenplottern geworden, stellen sich zwei Fragen:

• Zeigt der Funktionenplotter hier tatsächlich Grundverkehrtes an?

• Oder gibt er uns einen entscheidenden Tipp, nämlich auf eine sogenannte "hebbare Polstelle"?

Im vorliegenden Fall ist Letzteres der Fall - nur hätten wir es ohne Vorüberlegungen anhand der Wertetabelle gar nicht bemerkt: der Funktionenplotter glättet das Außergewöhnliche und Interessante völlig, er macht es unsichtbar.

Bzw. dass für x = 0 etwas Merkwürdiges passiert, sieht man erst, wenn man - und zwar erst aufgrund der Vorüberlegungen! - dort mal hinein zoomt:

• auf den ersten Blick sieht man nun, dass der Funktionenplotter auch auf der y-Achse (in blau) einen Ausschnitt des Graphen anzeigt;

• auf den zweiten Blick scheint er damit Grundverkehrtes gemacht zu haben:

  • er scheint den größten aller Fehler gemacht, nämlich doch durch 0 geteilt zu haben,

  • indem der Graph dort senkrecht wird, stellt er nicht mal mehr eine Funktion dar;

• auf den dritten Blick erkennt man aber, dass die blaue Linie ein wenig schief ist:

  • zwischen 0 und 2 liegt sie noch fast auf der y-Achse,

  • zwischen 2 und 4 liegt sie ein wenig weiter rechts.

  Liegt da also doch die erwartete Asymptotik vor?

Von hier aus wäre also überhaupt erst die Frage interessant, was in der Umgebung von x = 0 genau mit der Funktion bzw. dem Graphen passiert.

Oder vereinfacht: was passiert mit

• x,

• sin(x)

• und in Folge davon ^sin(x)/_x

in der Umgebung von x = 0?:

(womit man dann nebenbei einen schönen Nebeneingang zur Ableitung [hier der Sinusfunktion] gefunden hätte)