über den Umgang mit solch scheußlichen Zahlen wie und π

Jetzt mime ich mal kurz den kleinkarierten Klugscheißer:
der münsteraner Fahrer des Wagens mit diesem Kennzeichen
ist vermutlich Physiker oder Techniker,
aber garantiert nicht Mathematiker,
denn π ist nicht exakt, sondern nur ungefähr 3,141
- und was interessiert mich ein Näherungswert?! 

Von wegen "scheußliche Zahlen": da muss doch sofort kurz erwähnt werden, dass Mathematiker solche Zahlen wie und π keineswegs scheußlich, sondern durchaus reizvoll finden, gerade weil sie so geheimnisvoll sind.

Es ist nunmal leider (?) so, dass man sich in der Mathematik manchmal

(und an zentralen Stellen)

• bei den einfachsten, sogar jedem Kind verständlichen Aufgaben
• umgehend die größten Probleme einhandelt:

erstes Beispiel: wir nehmen uns die einfachste nur denkbare Tischplatte: sie ist quadratisch mit der Seitenlänge 1 m:

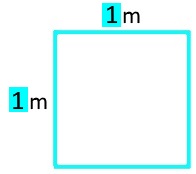
Auf diese Tischplatte zeichnen wir eine der einfachsten Linien, nämlich die Diagonale d:

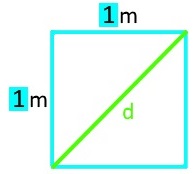
So weit, so einfach. Leider stellt sich aber bei Anwendung des Satzes des Pythagoras

(was hier nicht näher erklärt sei)

heraus, dass diese Diagonale d eine wahrhaft teuflische Länge hat, nämlich m, wobei ≈ 1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 7846210703 8850387534 3276415727

(was - wohlgemerkt - "nur" die ersten hundert Nachkommastellen von sind).

Noch ein bisschen genauer:

(Wer damit noch immer nicht zufrieden ist, kann hier die ersten millionen Nachkommastellen von bewundern).

Zweites Beispiel: vgl.