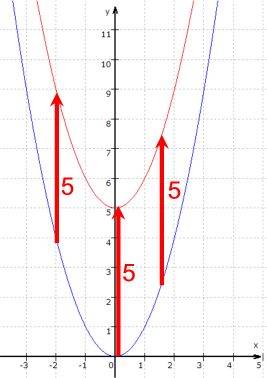
wenn SchülerInnen y = x² + 5 nicht verstehen, hat die Schule versagt

Der Fall ist so ähnlich in einer Klassenarbeit aufgetreten, nur habe ich ihn hier vereinfacht

(statt einer nach oben verschobenen Exponentialfunktion habe ich hier der Einfachheit halber eine nach oben verschobene Parabel genommen).

Damit ist auch schon gesagt, was "+ 5" bewirkt, nämlich eine Verschiebung der "Ausgangsfunktion" y = x²

(oder genauer: ihres Graphen)

um 5 nach oben:

D.h. mit dem gesamten blauen Graphen wird natürlich auch jeder Einzelpunkt dieses Graphen um 5 nach oben verschoben (oder umgekehrt).

Wichtig an dem Eindruck, den ich hier darstelle, ist dabei zweierlei:

• selbstverständlich waren solche Verschiebungen nach oben z.B. mittels "+5" schon mehrfach im Unterricht besprochen worden,
• aber die konkrete Verschiebung einer Parabel noch nicht.

D.h. die Aufgabe "y = x² + 5" verlangte schon einen gewissen "Transfer".

Dennoch trat bei mir während der Korrektur der Klassenarbeit ein geradezu typischer "Doppler"-Effekt ein:

1. schiere Enttäuschung, dass die allerwenigsten SchülerInnen "das" konnten, ja, vielleicht sogar ein wenig der Vorwurf: "Wie kann man denn so blöd sein, sowas Einfaches nicht zu können";
2. dann aber und sozusagen im "Rückschlag" der Vorwurf an mich selbst: "Wenn du ihnen nichtmal das vermitteln konntest, was hast du ihnen dann denn überhaupt vermittelt? - nämlich nichts!"

Das ist also zu allererst ein Selbstvorwurf, der dann allerdings

(ohne mich damit entschuldigen zu wollen)

auch weiter greift:

1. was haben denn die VorgängerlehrerInnen in früheren Klassen beigebracht? (nichts!)

(wohlgemerkt: die waren nicht schlechter als ich, sondern genauso schlecht; noch genauer: ich habe einen Heidenrespekt vor den didaktisch-methodischen Fähigkeiten einiger KollegInnEn und bin mir nicht so sicher, ob ich selbst so "gut" wie sie bin),

2. was bringt überhaupt der typische Matheunterricht ("die" Schule) bei? (nichts!)

Nun sind "schlecht" und "nichts" natürlich arg hoch gegriffen - und doch ist da was dran: wir ([Mathe-]LehrerInnen) haben doch immer wieder

(und insbesondere in Klassenarbeiten)

das Gefühl, dass - fast schon euphemistisch gesagt - reichlich wenig von dem, was wir so gut vermittelt zu haben meinten, wirklich angekommen ist.

Klassenarbeiten

(wenn das Kind also bereits in den Brunnen gefallen ist)

sind die Stunde der Wahrheit und der Spiegel, in dem der Lehrer eben auch, wenn nicht sogar vor allem sich selbst sieht.

Und wie oft denkt man dann doch als Lehrer: "Wenn ich geahnt hätte, dass die (viele) SchülerInnen dieses oder jenes nicht verstanden haben, hätte ich es doch viel ausführlicher besprochen."

(Hier seien mal die vielfältigen Gründe weggelassen, warum man es vorher [also rechtzeitig] nicht bemerkt hat.)

Nun mag man sich streiten, ob die "Funktionenlehre" samt gründlichem Verständnis der Form und (hier) Lage spezieller Funktionsgraphen eigentlich so wichtig ist

(immerhin sehen die Lehrpläne und wohl auch die meisten MatheleherInnen das als ungeheuer wichtig an).

Aber bei "+ 5" geht es ja um viel Grundsätzlicheres, nämlich ein Grundverständnis

1. des mathematisch zentral wichtigen Koordinatensystems,
2. der Zuordnung x |→ y

(denn durch "+ 5" wird jeder [also egal welcher] Funktionsgraph komplett um 5 nach oben verschoben, d.h. noch wichtiger als y = x² +5 ist y = Dingsbums + 5).

Oder anders gesagt: bei "+ 5" geht's ans Eingemachte dessen, was vielleicht nicht "an sich" wichtig ist, aber zumindest in der Schulmathematik als wichtig angesehen wird.

Ein Parallelbeispiel

(das ebenfalls ein wenig vereinfacht wurde):

in einer Oberstufenklausur kam die Funktionenschar y = x² + a vor und war gefragt, für welches a sie ein Minimum mit dem y-Wert 5 hat.

Die SchülerInnen haben das auch

(teilweise richtig, teilweise falsch, teilweise gar nicht)

brav ausgerechnet, sich aber nicht mal gewundert, dass das "ausgerechnet" für a = 5 klappte

(also im oben gezeigten Fall y = x² + 5 ).

Und sie konnten auch gar nicht einschätzen, ob ihr Ergebnis richtig war.

Da kann man nur sagen: sie haben leider

(allzu umständlich)

gerechnet, gerade weil sie nicht das mindeste Grundverständnis von

• Parabeln,
• dem Koordinatensystem,
• Zuordnungen

hatten.

(Ich spreche hier [wie öfters] der Einfachheit halber von "den" SchülerInneN, obwohl doch so einige darunter waren, die sehr wohl alles verstanden hatten.)

Mehr noch: ihnen war nicht einmal aufgefallen, dass eine simple

(dann nur noch um 5 nach oben zu verschiebende)

Normalparabel vorlag - jegliche Rechnung also überflüssig war.

(Man könnte fast sagen, dass da eine Gemeinheit des Lehrers vorlag, der eine ganz simple Aufgabe zwischen schwierigeren Aufgaben versteckt hatte - damit die SchülerInnen es nicht bemerkten?)

Anders gesagt: vor lauter Ableiten, das sie weitgehend gut beherrschten, hatten die SchülerInnen jegliche Grundlagen vergessen und jegliche Anschauung verloren

(wenn sie die denn jemals hatten).

Und das finde ich schlichtweg tragisch, ja, da ist im Matheunterricht etwas gründlichst schief gelaufen

(nochmals: ich mache da nicht einem Einzellehrer, sondern dem "System" Schulmathematik [dessen Teil ich in meiner zeitweisen Phantasielosigkeit bin] einen Vorwurf).

Es reicht nicht, über "unsere" Unfähigkeit zu klagen. Was also tun?:

1. Das Koordinatensystem samt der Zuordnungen in ihm muss viel gründlicher und immer wieder durchgenommen werden.
2. Es darf keine einzige Funktionsgleichung/kein einziger Funktionsgraph "durchgerechnet" werden

(auch und gerade nicht in der Oberstufe),

ohne dass

• vor jeder Rechnung überlegt wird,
  • was für eine Funktionsklasse (z.B. Parabel) vorliegt,
  • wie das grundsätzliche Verhalten des Graphen aussieht

(Streckung, Stauchung, Öffnung, Verschiebung)

• was eventuelle Zusatzaufgaben (s.o. Minimum mit dem y-Wert 5) anschaulich bedeuten,

• nach der Rechnung die rechnerischen Ergebnisse mit den vorherigen anschaulichen Überlegungen verglichen werden.

Bei all dem wird man auch mal rechnerisch schludrig sein dürfen, wie sich schön an dem doch eigentlich noch relativ einfachen (?) Bespiel y = x² - 6x + 14 zeigen lässt.

Da ist vor allem wichtig, dass der Teil-Term -6x + 14 die Normalparabel x² nur "irgendwie" (horizontal und/oder vertikal) verschiebt, dass aber - und das ist doch das entscheidend Wichtige! - nach wie vor eine Normalparabel vorliegt!

Denn die Rechnung, mit der man herausfinden kann, wie da genau verschoben wird, ist bereits keineswegs mehr so einfach und selbstverständlich:

y =  x² - 6x                          + 14 =

                                                        "quadratische Ergänzung" zwecks Herstellung des " 2. Binomi"

   =  x² - 6x + (⁶/₂)² - (⁶/₂)² + 14 =

   =  x² - 6x +   3²    -    3²   + 14 =

   = (x  -           3)²   -    9     + 14 =

   = (x  -           3)²            + 5

Und daraus überhaupt erst kann man dann entnehmen, wie die Verschiebung der Normalparabel genau aussieht:  um 5 nach oben und um 3 nach rechts ("ins Positive").

y =  x² wird also

• nicht (wie man erst meinen könnte) um 14,
• sondern um 5 nach oben verschoben.

Bzw.

• nicht die Funktion y =  x²,
• wohl aber die (bereits seitlich verschobene) Normalparabel y =  x² - 6x wird um 14 nach oben verschoben.

Allemal irritierend ist auch die horizontale Verschiebung: obwohl (oder gerade weil) da "minus 3" steht, wird "ins Positive" verschoben

(vgl. ).

Ich meine, es sollte viel weniger derart minutiös gerechnet und umgeformt werden

(und jede Wette: die SchülerInnen können's im besten Fall kurzfristig in der nächsten Klausur - und vergessen es dann verlässlich wieder komplett),

dafür aber um so mehr das grundsätzliche Verhalten/Aussehen von Funktionen betrachtet werden.

Die Klagen sind alt:

1. "Die SchülerInnen waren noch nie so dumm wie schon immer."
2. "Da haben wir es allergründlichst durchgenommen, und ein halbes Jahr später können die SchülerInnen dennoch [oder gerade deswegen?] nichts mehr davon."

Irgendwann wird man aus solchen Klagen die einzig wahre Konsequenz ziehen müssen: