Heiner Stauff - anschauliche Mathematik

lass' die Zahlen tanzen

(da heißt ein Rapper tatsächlich Prinz π [ehemals Prinz Porno,
was zwar ein bisschen pubertär klingt, aber eben doch auch nahelegt,
dass Zahlen sexy sein können!)

A-Wop-bop-a-loo-lop a-lop-bam-boo
(Little Richard: Tutti frutti)

, , o'clock, o'clock, rock,
, , o'clock, o'clock, rock,
, , o'clock, o'clock, rock,
We're gonna rock around the clock tonight.
(Bill Haley: Rock around the clock)

Neu ist es wahrhaft nicht, was ich hier sage:

sowieso nicht "weltgeschichtlich",
habe ich´s ja so ähnlich schon in gesagt, nur bringe ich hier neue Beispiele und werde zunehmend zwecks Vermittlung von Mathematik plakativer.

Mathematiker haben schon einen speziellen Knall, bzw. wer an sowas keine Freude hat (entwickelt), wird nie ein richtiger Mathematiker:

( Godfrey Harold Hardy)

Der Mathematik Hardy besucht eines Tages (1917) Ramanujan im Krankenhaus in Putney, das er mit Hilfe eines Taxis mit der Nummer 1729 erreichte.
Hardy zu Ramanujan: "1729 = 7•13•19 scheint eine langweilige Zahl zu sein!"
Ramanujan: "Ganz und gar nicht, es ist die kleinste Zahl, die sich auf mehr als eine Weise als Summe von zwei dritten Potenzen schreiben lässt: 1729 = 1³ +12³ = 9³ +10³."

( Srinivasa Aiyangar Ramanujan)

Das ist die unschuldigste, verspielteste Form der Hardcore-Wissenschaft "Zahlentheorie".

Aber wie mag Ramanujan drauf gekommen sein?:

Hatte er die Zahl 1729 schon mal vorher untersucht und sich nun "nur" daran erinnert

(was immerhin ein phänomenales Zahlengedächtnis voraussetzen würde, denn es gibt ja noch zig und hunderte andere interessante Zahlen)?

Einem Megagenie wie Ramanujan wäre allerdings zuzutrauen, dass er solchen Zahlen wie eben 1729 ihre speziellen Eigenschaften auch spontan ansehen konnte.

Letzteres hat, umgekehrt auf uns Normalsterbliche bezogen, aber die Folge, dass wir der Beschreibung von Zahleneigenschaften wohl nur andächtig zuschauen können: wir werden den Zahlen diese Eigenschaften (etwa im Schulunterricht) wohl kaum ansehen, sondern Zahlen höchstens teilweise konstruieren können (z.B. Dreieckszahlen).

Ich entnehme meine Beispiele im Folgenden dem wunderhübschen (und spottbilligen!) Büchlein

Spencer behandelt in diesem Buch die natürlichen Zahlen von 1 bis 100, und davon sei hier ein beliebiges Beispiel, nämlich die 81, herausgenommen:

Daran ist aber nur die erste, innermathematische Anmerkung interessant, während das über Mr Burns Gesagte ein netter Gimmick bzw. Zufall ist.

Auch hier zeigt sich also sehr schnell, wer ein "guter" Mathematiker ist:

ihn interessieren nur rein innermathematische Eigenschaften,
aber doch nicht irgendwelche äußeren Zufälle

(für ihn ist also etwa die Hälfte von Spencers Buch völlig uninteressant).

Die in der ersten Anmerkung genannten Eigenschaften sind, wie gesagt, rein innermathematisch, d.h. sie machen keinerlei äußeren Sinn und sind auch wohl kaum - wie schnöde - "anwendbar".

Schon allein an der 81 wird aber deutlich, dass die scheinbar stumpf hintereinander gereihten natürlichen Zahlen, also

1,2,3,4,5,6,7,8,9,10,11 ...,

regelrecht einen Text (= Gewebe) aus vielen verbindenden Eigenschaften haben. So ist 81

zwar die einzige Zahl, deren Quadratwurzel gleich der Summe ihrer Ziffern ist

(und doch gibt es auch zwei triviale andere Zahlen, nämlich 0 und 1, die dieselbe Eigenschaft haben),

aber eine Quadratzahl wie viele andere (aber nicht alle) auch
und eine Siebeneckzahl wie wiederum viele andere (aber nicht alle) auch.

(Nebenbei: das wird hier wie in dem Buch alles nur behauptet und wäre doch eines Nachweises/einer genaueren Untersuchung wert.)

Und so werden die natürlichen Zahlen eben von vielfältigen Strukturen durchzogen:

gerade/ungerade Zahlen,
Quadratzahlen/Potenzen kleinerer Zahlen,
Primzahlen (vgl. ), darunter insbesondere Mersennesche Primzahlen/zusammengesetzte Zahlen,
Fibonacci-Zahlen,
vollkommene Zahlen,
abundante Zahlen,
Dreieckszahlen,
Palindrome,
Fermatzahlen,
Lucas-Zahlen,
pentagonale Zahlen,
hexagonale Zahlen,
Siebeneckzahlen,
Fakultätszahlen,
glückliche Zahlen,
Ulam-Zahlen,
Primoriale,
stark zusammengesetzte Zahlen,
...
... und das allein schon unter den Zahlen 1 bis 100!

Durchaus lustig finde ich, dass die 39

(nach immerhin bereits 38 interessanten Zahlen!)

mal als "die erste uninteressante Zahl" bezeichnet wurde, worauf Spencer allerdings sofort antwortet:

"Zwar ist sie nicht so sexy wie die 7 oder so fesch wie die 99, aber sie hat doch auch einiges für sich. Zum Beispiel: 39 = 3•9+3+9."

Bemerkenswert sind auch die blumigen Worte der Mathematiker, also z.B. "vollkommene" oder "glückliche" Zahlen, was aber wiederum nur Innermathematisches bedeutet:

"Vollkommene Zahlen sind solche, die gleich der Summe ihrer Faktoren sind (sie selbst nicht eingeschlossen). Man kann [z.B. die kleinste vollkommene Zahl] 6 darstellen als 1•6 und 2•3. Wenn wir die Faktoren addieren, erhalten wir 1+2+3=6."
"Um wirkliche glückliche Zahlen zu finden, schreiben Sie eine lange Reihe von Zahlen auf, sagen wir von 1 bis 100. Streichen Sie nun die Zahl 2 [...] und außerdem jede weitere 2. Zahl. Die Reihe sieht nun so aus: 1, 3, 5, 7, 9, ... Die nächste Zahl ist die 3, also streichen Sie jetzt jede 3. Zahl. Die Reihe lautet jetzt 1 , 3, 7, ... Streichen Sie jede 7. Zahl, die noch da ist, dann jede 9. und machen Sie nach diesem Schema weiter. Übrig bleiben alle glücklichen Zahlen."

(z.B. die glückliche Zahl 25; "glücklich" vielleicht deshalb, weil sie das Glück hatte, nicht der rabiaten "Dezimierung" zum Opfer zu fallen.)

Nur ein Beispiel dafür, dass Zahlen nicht bloß solo tanzen

(z.B. "ich bin eine Primzahl, und es interessiert mich nicht die Bohne, ob´s noch andere Primzahlen gibt"),

sondern auch zusammen eine Art "squaredance" tanzen können:

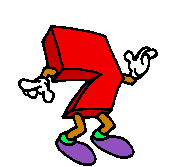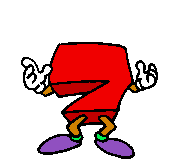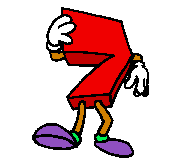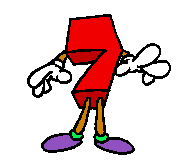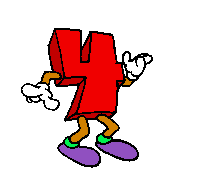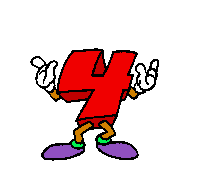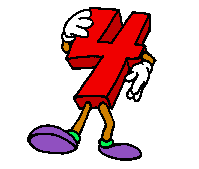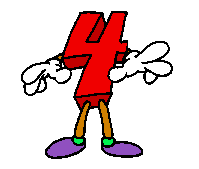+++== ² die ersten 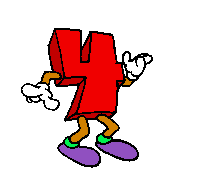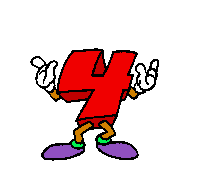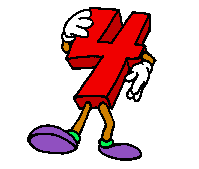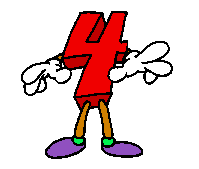ungeraden Zahlen

In Worten: die Summe der ersten 4 ungeraden natürlichen Zahlen ist gleich 4². Wohlgemerkt: dabei kommt die 4 gar nicht als Summand vor (weil sie ja nicht ungerade ist), sondern ist - schon erheblich abstrakter - die Anzahl der Summanden. Woher aber "wussten" die Summanden, dass

sie insgesamt 4 sind
und ihre Summe 4² ist ???

Und in der Tat gilt, was man anhand des Beispiels vermuten könnte, dass nämlich die Summe der ersten n ungeraden natürlichen Zahlen n² ist.

(Den Beweis mittels der aberwitzig-hochinteressanten vollständigen Induktion lasse ich hier aber weg.)

Im üblichen Schulunterricht werden (natürliche) Zahlen einfach nur als stumpf aufeinander folgend hingenommen, wird also nie über sie gestaunt und lässt man sie auch niemals tanzen:

PS:

"»Tauga«, das ist eine Zahl auf Polynesisch. Genauer gesagt: Eine Zahl in der polynesischen Sprache Mangareva. Sie bedeutet zwei. Oder vier. Oder acht. Je nachdem, ob gerade Zuckerrohr, Brotfrüchte oder Kraken gezählt werden. Solch ein »objektbezogenes« Zahlsystem, in denen die Zahlen nicht unabhängig sind von den Gegenständen, auf die sie sich beziehen, mutet für uns im modernen Europa merkwürdig an. Wir zählen abstrakt: Eins, zwei, drei – bis unendlich: Die gleichen Zählwörter für alles."
(zitiert nach )