die Zahl, das unbekannte Wesen
LeserInnen könnten (zunehmend?) den Eindruck gewinnen, ich
-
halte sämtliche SchülerInnen für mathematisch "schwerstbehindert" und deshalb extrem hilfsbedürftig,
-
differenziere das Selbstverständliche und "eigentlich" Einfache so lange tot, bis es garantiert äußerst schwierig ist (Augustinus: "Was ist Zeit?"). Und das ausgerechnet unter dem Obertitel  :-)
:-)
Dabei meine ich nur, dass
-
sehr viele SchülerInnen Probleme haben (bzw. alle immer mal wieder)
(womit ich eben nicht PISA-Probleme, also z.B. die deutscher SchülerInnen im internationalen Vergleich meine, sondern solche, die jedeR AnfängerIn [also auch Finnen!] mit Mathematik hat bzw. haben kann;
die PISA-Probleme werden hier höchstens nebenher mitgelöst [?], was mir überhaupt die einzig richtige Einstellung zu sein scheint:
machen wir bessere Mathematik, statt ununterbrochen gebannt [paralysiert] auf PISA zu schielen und [dann sowieso aussichtslos] PISA hinterherzuhecheln!),
-
man diesen Problemen nur "beikommen" kann
(was nicht heißt, sie für die SchülerInnen vorsorglich aus dem Weg zu räumen; sondern teilweise kann man die SchülerInnen dann nur um so besser mit diesen Problemen konfrontieren),
wenn man sich ihre fundamentalen Wurzeln mal wirklich klar macht, also erkennt, dass diese Probleme keineswegs auf die allbekannte Dummheit der "Jugend von heute" zurückzuführen, sondern in der Mathematik selbst angelegt, also - selbst bei den intelligentesten SchülerInneN - schlicht unvermeidbar, wenn nicht sogar das Salz in der mathematischen Suppe (die eigentliche Mathematik) sind,
-
LehrerInnen (nicht vollständig vermeidbar?) oftmals betriebsblind für solche Probleme sind (sie für künstlich erzeugt und übertrieben halten; s.o.), weil sie bereits vollständig begriffen haben (?) und von der Fachsystematik aus denken; vor allem aber, weil sie leugnen bzw. vergessen oder verdrängt haben, dass sie selbst mal solche Probleme hatten;
-
ich ja sowieso nicht (in erster Linie) für SchülerInnen, sondern für LehrerInnen (letztlich mich selbst) schreibe: meine "Totdifferenzierungen" mögen teilweise wirklich nicht für die Hände von SchülerInnen geeignet sein, weil sie da evtl. nur vollends irritierend ankommen.
So langsam bricht - glücklicherweise! - (m)eine Welt zusammen:
(ohne die Probleme auch mit diesen zu verkennen)
immer aus zwei Gründen gegen Dezimalzahlen verteidigt:
-
; vgl.  , aber auch
, aber auch  :
:
Brüche seien viel genauer (nämlich exakt!) als die meisten Dezimalzahlen
(z.B. ist 1/3 absolut exakt, während da jede Dezimal-Computeranzeige [also z.B. 0,3333333333] hinten abgehackt, also ungenau [und somit für MathematikerInnen nachgerade uninteressant] ist),
-
, vgl. wieder  :
:
Brüche seien viel anschaulicher als Dezimalzahlen bzw. im Gegensatz zu vielen von diesen oftmals überhaupt erst anschaulich
(z.B.
-
1/3 im Vergleich mit 0,333333333... oder auch 0,3
-
und allemal 1/7 im Vergleich mit 0,14285714285714285714285714285714... oder auch 0,142857;
-
spätestens aber unter 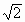 kann ich mir [fast] nichts mehr vorstellen, wenn ich auch immerhin noch die Größenordnung kenne, da ich weiß, dass
kann ich mir [fast] nichts mehr vorstellen, wenn ich auch immerhin noch die Größenordnung kenne, da ich weiß, dass 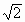 ungefähr 1,41421 ist [und dahinter geht´s - igitt! - irrational weiter];
ungefähr 1,41421 ist [und dahinter geht´s - igitt! - irrational weiter];
-
und z.B. bei 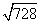 bricht dann meine Vorstellungskraft [fast] endgültig zusammen, weil ich da nicht mal mehr den Dezimalwert und damit die Größenordnung [beinahe der einzige Vorteil der Dezimalzahlen] kenne
bricht dann meine Vorstellungskraft [fast] endgültig zusammen, weil ich da nicht mal mehr den Dezimalwert und damit die Größenordnung [beinahe der einzige Vorteil der Dezimalzahlen] kenne
[auf die unscheinbar-hinterhältige Einschänkung "fast" wird dringend zurückzukommen sein!]),
Der erste Grund, also die Genauigkeit, bleibt zweifelsohne bestehen.
Beim zweiten (somit also Pseudo-?)Grund habe ich inzwischen aber meine erheblichen Zweifel
(und kann damit typische Schülerprobleme viel besser verstehen - und auch angehen?).
Wenn aber sogar die Brüche (also nach den ganzen Zahlen die nächstschwierigeren Zahlen) weitgehend unanschaulich sind, so bleibt (außer eben den ganzen Zahlen; und wir werden unten sehen, dass selbst diese nicht so selbstverständlich sind, wie man auf den ersten Blick meinen sollte) fast nichts mehr übrig, sind also fast alle Zahlen unanschaulich. Wundern einen da noch typische Schülerprobleme, und zwar beim noch relativ einfachen Rechnen?! |
Um meinen SchülerInneN die Angst vor Unbekannten (also in erster Linie x) zu nehmen, habe ich ihnen oft gesagt, mit diesen Unbekannten rechne man (mit wenigen Ausnahmen) genauso wie mit Zahlen
("tut einfach so, als sei x eine Zahl"),
weil sich hinter den Unbekannten ja auch tatsächlich (nur anfangs unbekannte) Zahlen verstecken (vgl.  ).
).
Wie mir inzwischen aufgeht, war dieser Tipp keineswegs so eindeutig gut, wie ich gedacht hatte
(und dennoch behält er seinen Wert!):
nämlich dann nicht, wenn, wie soeben gezeigt, auch die Zahlen weitgehend unanschaulich, im Grunde also auch nur "Unbekannte" sind.
Nun kann man aber glücklicherweise den Spieß umdrehen und auf einem Umweg von den (schwierigeren) Unbekannten etwas für die (scheinbar oder tatsächlich einfacheren) Zahlen lernen:
-
"Rechne mit Unbekannten wild nach den für Zahlen üblichen Rechengesetzen los - und du wirst [abgesehen unlösbaren Fällen] am Ende verlässlich ein klares Ergebnis bekommen!"
-
"Üblicherweise gilt dasselbe für Zahlen: oftmals werden auch sie erst durch Rechnen anschaulich."
Und selbst da kann man wieder aus dem Schwierigen für das (scheinbar) Einfache lernen. Fangen wir also mit "schwierigen" Wurzeln an, um danach zu "einfachen" Brüchen zu kommen:
Ich hatte oben gesagt, dass ich mir unter 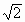 (und allemal unter
(und allemal unter 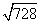 ) "fast" nichts mehr vorstellen kann. "fast", denn eins weiß ich doch immerhin, nämlich die Definition, also sozusagen das "Grundwesen" der Wurzel:
) "fast" nichts mehr vorstellen kann. "fast", denn eins weiß ich doch immerhin, nämlich die Definition, also sozusagen das "Grundwesen" der Wurzel:
(Wenn ich die Logik dahinter auch kenne, bleibt sie mir dennoch weitgehend unanschaulich: dass 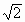 •
• 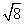 , also das Produkt zweier teuflisch irrationaler "Schlangen", exakt gleich 16 ist und damit sogar eine ganz einfache natürliche Zahl, erstaunt mich dennoch immer wieder, ja erfüllt mich fast mit Bewunderung, und zwar insbesondere, wenn ich mir die jeweils irrationalen Dezimalschreibweisen anschaue:
, also das Produkt zweier teuflisch irrationaler "Schlangen", exakt gleich 16 ist und damit sogar eine ganz einfache natürliche Zahl, erstaunt mich dennoch immer wieder, ja erfüllt mich fast mit Bewunderung, und zwar insbesondere, wenn ich mir die jeweils irrationalen Dezimalschreibweisen anschaue:
-
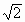 ≈ 1,4142135623731
≈ 1,4142135623731
-
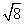 ≈ 2,8284271247461
≈ 2,8284271247461
Nun bin ich ja nicht völlig blöd: die zweite Zahl ist erkennbar und aus gutem Grund das Doppelte der ersten.)
| Die Wurzeln 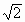 und und 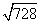 haben also an sich wenig Sinn, sondern finden ihn erst durch Rechnen (Quadrieren bzw. Multiplizieren mit sich selbst). haben also an sich wenig Sinn, sondern finden ihn erst durch Rechnen (Quadrieren bzw. Multiplizieren mit sich selbst). Und Rechnen ist für mich eine Tätigkeit. |
(Genau genommen sind Wurzeln überhaupt erst durch dieses Rechnen, also indirekt bzw. "um die Ecke", definiert:
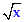 ist definiert als diejenige [ansonsten völlig uninteressante] Zahl, deren Quadrat x ergibt: mehr weiß ich nicht - und muss ich auch nicht wissen. Ich kann dennoch prächtig damit hantieren, sprich: rechnen.
ist definiert als diejenige [ansonsten völlig uninteressante] Zahl, deren Quadrat x ergibt: mehr weiß ich nicht - und muss ich auch nicht wissen. Ich kann dennoch prächtig damit hantieren, sprich: rechnen.
Ich habe hier sogar bewusst allgemein von 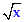 statt konkret z.B. von
statt konkret z.B. von 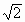 gesprochen: nichtmal die 2 [also eine konkrete Zahl!] ist noch interessant, bzw.
gesprochen: nichtmal die 2 [also eine konkrete Zahl!] ist noch interessant, bzw. 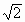 ist auch nicht einfacher als
ist auch nicht einfacher als 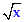 .)
.)
Genauso verhält es sich aber mit Brüchen
- und da muss man wahrhaft nicht zu äußerst komplizierten Brüchen greifen, sondern es reicht beispielsweise solch ein doch noch ziemlich einfacher Bruch wie 7/9 .
Bereits 7/9 ist für mich weitgehend unanschaulich, aber eins
(nur als Beispiel)
weiß ich dennoch ganz genau: 7/9 • 9 ergibt (ist) exakt 7 :
"Ich verteile sieben Kuchen an neun Leute und schmeiße dann
(z.B., weil keiner Hunger auf Kuchen hat)
alle neun Anteile der Leute wieder zusammen; kein Wunder, dass das dann wieder die ursprünglichen sieben Kuchen sind."
- wobei ich, wohlgemerkt!, keinerlei Vorstellung davon haben muss, dass 7/9 (der Anteil jedes der Leute) etwa so aussieht:
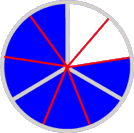
(Unsere neueste Erkenntnis sollte einen auch gar nicht wundern: 7/9 ist ja keineswegs eine von Anfang an fertige Zahl, sondern selbst schon Ergebnis einer Rechnung, und zwar einer relativ abstrakten Division.
"Die ganzen Zahlen schuf der liebe Gott, alles übrige ist Menschenwerk."
(Leopold Kronecker)
Die nachfolgende Multiplikation mit 9 ist nicht nur als Rechenart erheblich einfacher, sondern als Gegenrechnung zur vorherigen Division durch 9 sowieso trivial.)
Man könnte Zahlen also fast mit Substantiven/Subjekten in der Sprachwissenschaft vergleichen:
(vgl.: man kommt mit der [von Extremfällen abgesehen] unveränderlichen Grundeigenschaft "weiblich" oder "männlich" auf die Welt),
(vgl.: das unveränderlich weibliche Wesen kann in verschiedenen Lebensphasen und sozialen Kontexten völlig unterschiedliche "Funktionen" haben, nämlich z.B. erst SchülerIn [und nachmittags Jugendgruppenleiterin], später Studentin ... sein).
Nun braucht man für die Erkenntnis, dass Dinge in verschiedenen Kontexten auch verschiedene Bedeutungen annehmen, allerdings nichtmal die Grammatik zu bemühen: in
hat ein und dasselbe Wort, nämlich "Gnade", offensichtlich völlig unterschiedliche Bedeutungen.
In den beiden Beispielsätzen scheint mir das Wort "Gnade" derart unterschiedliche Bedeutungen zu haben, dass ich mich frage, ob es überhaupt "die" lexikalische, kontextfreie Bedeutung gibt.
Und eben genauso scheint es mir bei fast allen Zahlen!
| Sowieso ist Mathematik weitgehend der Umgang mit Unbekanntem (bzw. nicht mit schnöden Einzelfällen), das aber in Verbindung miteinander gebracht wird. |
Ich hatte oben ein "Patentrezept" für den Umgang mit Unbekannten (also in erster Linie x) genannt:
"[...] mit diesen Unbekannten rechne man [...] genauso wie mit Zahlen [...], weil sich hinter den Unbekannten ja auch tatsächlich (nur anfangs unbekannte) Zahlen verstecken [...]"
Vielleicht wurde damit aber nur der Teufel durch Beelzebub ausgetrieben oder ist es sogar ein Zirkelschluss, wenn - wie gezeigt - die meisten Zahlen
(nicht nur für viele SchülerInnen)
auch nur "Unbekannte" sind.
Oben war schon angedeutet worden, dass nichtmal ganze oder sogar natürliche Zahlen problemlos sind:
-
verbinden wir mit sehr großen natürlichen Zahlen auch kaum mehr eine Anschauung (vgl. nochmals  ),
),
-
hat Bertrand Russell es sogar geschafft, die simpelste aller Zahlen, nämlich die Eins, totzudifferenzieren (aus dem Nichts zu erschaffen),
-
befasst sich die "Königin der Mathematik", nämlich die Zahlentheorie, ausschließlich mit den einfachsten, also natürlichen, Zahlen - und gilt (paradoxerweise?) doch als eines der schwierigsten Gebiete der Mathematik.
In der Zahlentheorie passiert nun aber das Umgekehrte von oben Gesagtem:
(wo sollten beispielsweise bei folgenden Zahlen Probleme sein?: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163 ...),
Oder nehmen wir die berühmte Goldbach´sche Vermutung:
"Jede gerade Zahl, die größer als 2 ist, lässt sich als Summe von zwei Primzahlen ausdrücken."
Die geraden Einzelzahlen, also 4, 6, 8, 10 ..., sind zweifelsohne von absoluter Einfachheit, aber der Zusammenhang (nämlich mit zwei Primzahlen) ist teuflisch schwierig, denn die "Goldbach´sche Vermutung" ist eben seit Jahrhunderten und bis heute nur eine Vermutung, also unbewiesen
(man findet problemlos für jede einfache gerade Zahlen schnell zwei Primzahlen, deren Summe diese gerade Zahl ist, also z.B. 8 = 3 + 5; aber für einen Beweis wären alle geraden Zahlen, also unendlich viele, zu überprüfen, und genau dafür hat noch niemand eine typisch mathematische Abkürzung gefunden).
![]() :-)
:-)