selbstgewählte Schwierigkeitsniveaus

Am Beispiel der Symmetrie gewisser ganzrationaler Funktionen sei im Folgenden mal überlegt, wie eine Binnendifferenzierung im Unterricht, aber auch in Klausuren aussehen kann.

Vorausgesetzt sei dabei, dass die Symmetrie über Überlegungen zur Schönheit von Funktionsgraphen auftauchte (also über Anschauung, nicht Anwendung). D.h. der erste Zugang ist ein geometrischer, nicht algebraischer

1. Was müssen alle SchülerInnen lernen? (Obligatorik)

1. Unverzichtbar ist der Übergang von der geometrischen zur algebraischen Bedeutung von Symmetrie, d.h. von

zu

und dann zu f (x) = - f (-x).

Analoges gilt für achsensymmetrische Graphen.

Dahinter steckt die gar nicht deutlich genug hervorhebbare, wenn auch nur vorläufige Wahrheit, dass in der Schulmathematik zunehmend auch berechnet werden kann, was gezeichnet werden kann - und umgekehrt.

Vgl. Anmerkung unten.

2. das grundlegende Beweisverfahren, und d.h.:

immerhin der Nachweis, dass die Gleichung f (x) = - f (-x) für eine konkrete Funktion und ein konkretes x gilt, dass also z.B. f (4) = - f (-4) für die Funktion f: y = 5x³ + 7x gilt.

Hier muss immerhin noch gewusst und anschaulich gemacht werden, dass selbstverständlich mit der Symmetrie eines Punktes natürlich noch lange nicht die Symmetrie des ganzen Graphen bewiesen ist.

2. Freiraum

3. die SchülerInnen können die Symmetrie für alle Punkte einer konkreten Funktion beweisen, dass also z.B. f (x) = - f (-x) für die Funktion f: y = 5x³ + 7x gilt.
4. die SchülerInnen können die Symmetrie für alle Punkte einer ganzen Funktionsklasse beweisen, dass also z.B. f (x) = - f (-x) für die alle Funktionen der Art f: y = ax³ + bx gilt.

Diese Hierarchie ist nochmals auf einer anderen Ebene binnendifferenzierbar, nämlich je nach Funktionenklasse. Z.B.

• sind die Beweise für biquadratische Funktionen (Achsensymmetrie zur y-Achse) einfacher als
• die Beweise für Funktionen dritten Grades mit rein ungeraden Exponenten (Punktsymmetrie zum Ursprung, wobei zusätzlich das Minus zu beachten ist); und diese Beweise sind wiederum einfacher als
• solche bei (horizontalen und vertikalen) Verschiebungen:

so ist beispielsweise der allgemeine Beweis, dass alle (also auch gestreckte/gestauchten und verschobenen) quadratischen Parabeln

• achsensymmetrisch
• zu einer Parallelen zur y-Achse
• durch den Scheitelpunkt

sind, für SchülerInnen einer 10. Klasse schon arg schwierig, weil das ein unschönes Gewusel mit vielen (Form-)Variablen setzt.

Aber das heißt eben nicht, dass man mit SchülerInnen einer 10. Klasse gar nicht erst in solche "Höhen" aufsteigen sollte. Sondern im Gegenteil

• brauchen bessere SchülerInnen ab und zu "Futter" bzw. eine Herausforderung,
• muss schon bzw. spätestens in einer 10. Klasse angedeutet werden, wovon spätere Mathematik-LKs handeln, d.h. welche typischen Fragestellungen, aber auch welche Schwierigkeiten sich da ergeben werden.

(Und dann können SchülerInnen auch überprüfen, ob sie sich überhaupt für solche [inner-]mathematischen Fragestellungen interessieren.)

Nun kann man ja im Unterricht differenzieren, indem man die SchülerInnen parallel auf die verschiedenen Schwierigkeitsstufen ansetzt bzw. ihnen die Wahl lässt.

(Und es gibt immer wieder SchülerInnen, denen es eine "Ehre" ist, in Hausaufgaben auf solche Schwierigkeiten angesetzt zu werden.

Die "Ehre" entsteht auch dadurch, dass sie später ihre Ergebnisse allen MitschülerInnen vorführen, was unbedingt nötig ist, damit Binnendifferenzierung nicht zur völligen Zersplitterung führt. Und "Vorführen"

• vermittelt dann eben auch den "schlechteren" SchülerInnen das erworbene Wissen,
• fordert von den "besseren" eine verständliche Vermittlung: auch diese Verständlichkeit geht [zusätzlich] in die Leistungsbewertung ein).

Und genauso kann man auch Klassenarbeiten stellen

(wobei das Verfahren nur dann zweifelhaft wäre, wenn überhaupt nur eine Aufgabe dieser Art bzw. überhaupt nur solche Aufgaben auftauchen würden):

Die SchülerInnen können sich selbst ihre Schwierigkeitsstufe wählen:

2. eine konkrete Funktion, ein konkreter x-Wert,
3. eine konkrete Funktion, beliebiger x-Wert,
4. eine ganze Funktionenklasse mit beliebigen x-Werten.

Weil man nun aber nicht von SchülerInnen verlangen kann, dass sie sich freiwillig eine Aufgabe wählen, die automatisch (nur im Hinblick auf diese eine Aufgabe gerechnet) zu einem "mangelhaft" führt, darf es bei keiner richtigen Lösung von B., C. oder D. (und d.h. insbesondere bei der leichtesten Aufgabe B.) ≤ die halbe Punktzahl geben.

Zudem müssten SchülerInnen mindestens einen kleinen, eher lässlichen Fehler machen dürfen, ohne damit gleich über die "Kante" zum "mangelhaft" zu rutschen.

Denkbar wäre also folgende Bepunktung:

2. 12
3. 16
4. 20

(wobei die Dopplung der Punkte [statt z.B. 6, 8 und 10] deshalb gewählt wurde, damit andere [Standard-]Aufgaben relativ gering bewertet werden können.)

Das System schließt zudem nicht aus, dass jemand sich "hocharbeitet", also z.B.

• erst zur Sicherheit oder weil er sich anfangs nicht mehr zutraut B. löst
• und dann (etwa weil er bei B. doch noch auf die entscheidende Idee gekommen ist) doch noch C. oder gar D. löst.

Umgekehrt ist es ja auch für jemanden, der sich durchaus D. zutraut, empfehlenswert, es erst mal an B. auszuprobieren.

Klar dabei ist nur, dass man keine Punkte summieren kann bzw. dass die Höchstgrenze 20 Punkte ist und bleibt.

Ein weiteres schönes Beispiel für eine mögliche Binnendifferenzierung ist die Ermittlung der Kreisfläche mittels Parkettierung durch ein Quadrat und dann "außenrum" zunehmend feinere Dreiecke:

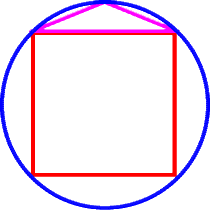
1. kann man das Prinzip gemeinsam herleiten oder aber EinzelschülerInnen  und Gruppen seine Entdeckung (angeleitet) überlassen;

2. sind verschiedene Schwierigkeitsgrade in Gruppen möglich:

• eine erste Gruppe zeichnet nur, wobei allerdings durchaus Grundprinzipien eingehen sollen,

• eine zweite Gruppe berechnet die Flächen des Quadrats sowie der Dreiecke der 1. und 2. Generation und dann - daraus folgend - des zugehörigen Vielecks,

• eine dritte Gruppe sucht nach der Formel für die Dreiecke der n-ten Generation sowie - daraus folgend - des Vielecks der n-ten Generation,

• eine vierte Gruppe erstellt ein Programm, das die Vielecke und ihre Fläche beliebig genau zeichnet und/oder berechnet,

• eine fünfte Gruppe macht dieselben Schritte für eine Annäherung von außen,

• eine sechste Gruppe kümmert sich nicht um die elementargeometrische, sondern um die funktionale Herleitung (Integration):

Wichtig dabei ist: alle Gruppen haben hinterher das Grundprinzip verstanden, und beispielsweise zeigen die "komplexeren" Gruppen den "einfacheren" hinterher "nur" die Verfeinerungen bzw. Weiterführungen des grundlegenden Prinzips.