Orientierungslauf "Grundwissen über Funktionen"

die Mittlerfunktion der 11. Klasse
die besondere Bedeutung "funktionaler Zusammenhänge"
der Lehrgang

Auszug aus dem Mathematik-Lehrplan für die 11. Klasse in NRW (vgl. ):

"Themen und Gegenstände

Jahrgangsstufe 11

Für die Jahrgangsstufe 11 sind Koordinatengeometrie, Beschreibende Statistik und Differentialrechnung ganzrationaler Funktionen vorgesehen. Sie knüpfen an die Standards für den mittleren Schulabschluss an (vgl. Kapitel 3.4) und führen in die Gebiete ein, die in der Qualifikationsphase unterrichtet werden. Nachfolgend sind die Unterrichtsthemen und -gegenstände stichwortartig aufgeführt und anschließend erläutert. Die aufgelisteten Inhalte sind verbindlich. Die Zusammenstellung ist äußerst kurz gehalten, um den Schulen einen möglichst weiten Raum für die Gestaltung des Unterrichts zu eröffnen [hört, hört!]. Daher ergibt sich bei Beschränkung auf diese Inhalte keine vollständige Lernsequenz. Ausweitungen, Akzentuierungen und Vertiefungen sind erforderlich.

Koordinatengeometrie

• Gerade, Parabel, Kreis

• Kreistangente, Parabeltangente

• Lineare Gleichungssysteme zur Bestimmung von Geraden und Parabeln.

Die Koordinatengeometrie knüpft an Inhalte des Mathematikunterrichts der Sekundarstufe I an. Sie bereitet auf Kernprobleme der Differentialrechnung vor und stellt Hilfsmittel für die Analysis zur Verfügung. Die zentralen Ideen des Messens, des funktionalen Zusammenhangs und des mathematischen Modellierens können deutlich werden.

Bei Geraden und Parabeln sollten Anwendungen (z. B. Scheinwerfer, Parabolantennen) Berücksichtigung finden. Scheitelpunktsbestimmungen können Optimierungsprobleme lösen helfen. Schnittprobleme zwischen Geraden und Parabeln bzw. Kreisen eröffnen unterschiedliche Zugänge zum Tangentenbegriff ohne Differentialrechnung. [...] Auch die systematische Behandlung linearer Gleichungssysteme in den Jahrgangsstufen 12 bis 13 kann vorbereitet werden. Schließlich ermöglicht die Koordinatengeometrie eine immanente Wiederholung wichtiger Themen aus der Sekundarstufe I (z. B. Koordinatensystem, Geradengleichung, Lösung quadratischer Gleichungen, Rechnen mit Quadratwurzeln, Anwendungen der Satzgruppe des Pythagoras und der Strahlensätze sowie der trigonometrischen Funktionen). Insofern eignet sie sich zur Angleichung des Wissensstandes unterschiedlicher Schülergruppen in besonderem Maße.

[...]

In der Differentialrechnung tritt bei der Erarbeitung von Gesetzmäßigkeiten die zentrale Idee des funktionalen Zusammenhangs in den Vordergrund."
(S. 14ff)

Dem ist (abgesehen von der Stochastik) insbesondere hinsichtlich des ersten Halbjahres der 11. Klasse zweierlei zu entnehmen:

1. Das Halbjahr hat eine Mittlerposition zwischen Altem und Neuem:

• das Halbjahr ist sozusagen "die letzte Tankstelle vor der Autobahn": letztmalig (???) erhalten die SchülerInnen die Gelegenheit, wichtige Inhalte der Unter- und Mittelstufe zu wiederholen, auf denen die weitere Oberstufenmathematik aufbaut;

• leider schätzen viele SchülerInnen solche Wiederholung gering ("hatten wir doch alles schon, gähn!") und meinen - auch in anderen Fächern -, die 11. Klasse sei letztlich nur eine überflüssige Wartestation und brauche man nur gelangweilt abzusitzen, bis die "eigentliche" Oberstufe ("der ernst des [Schul-]Lebens") beginnt;

• solche Geringschätzung ist aber auch verständlich, wenn da tatsächlich nur wiederholt wird;

• die Richtlinien deuten da mit "Ausweitungen, Akzentuierungen und Vertiefungen sind erforderlich" etwas Zusätzliches an, das ich - wo es so allgemein bleibt - folgendermaßen fülle:

  • eine Systematisierung und "theoretische" Einordnung des bereits Bekannten
    (also auch eine Bewertung der Bedeutungen),

  • neue Fragestellungen an Altbekanntes
    (z.B.: was haben alle Funktionen ungeraden Grades gemeinsam?),

  • vom bereits Bekannten aus Entwicklung von Fragestellungen für die weitere Oberstufenzukunft bzw. Ausformulierung von längst im Raum stehenden Fragen
    (z.B: "das Maximum [den Scheitelpunkt] quadratischer Funktionen können wir schon [berechnen], aber wie berechnet man graphisch längst bekannte [!] Extremwerte bei Funktionen höheren Grades?"
    Und nebenbei: wenn jemand [was häufig vorkommt, ja sogar fast die Regel ist] die Scheitelpunktsberechnung bei quadratischen Funktionen nicht mehr beherrscht, so kann man fast schon flapsig sagen: "das ist als 9.-Klasse-Stoff so einfach, dass wir´s mal ruckzuck wiederholen".)

  Den SchülerInnen muss das "Neue im Alten" deutlich werden, ja man kann sie vielleicht sogar bei ihrer "Ehre" packen:

• nicht: "euch Blödmännern muss man ja alles nochmals verklickern"
  (kein Wunder,  wenn sie solch einer [und sei´s latenten] Botschaft verweigern),

• sondern: "ihr seid Fachleute für den Mittelstufenstoff und dessen Aufarbeitung"

(z.B. kann man ja auch mal despektierlich sagen:

"5.-Klässler waren noch so blöd zu glauben ..., ihr aber [als erwachsene Menschen] wisst natürlich längst ...");

man könnte das Projekt ja wirklich so aufziehen, dass die 11.-Klässlern realen unteren Klassen den Stoff vermitteln.

Es ist also in der Tat Stolz darauf angesagt, was man [und sei´s die ganze Klasse zusammen] schon alles kann, und daraus kann der Mut (und die Motivation) erwachsen, demnächst (in der restlichen Oberstufe) auch noch "kurz" die "wenigen" verbleibenden Reste anzugehen.

Das 1. Halbjahr der 11. Klasse könnte dazu beitragen, dass die SchülerInnen

• bzgl. des bereits bekannten Stoffs endlich (aus übergeordneter Perspektive)

• die Routenplanung für die Oberstufe kennen, ja sogar - soweit ihnen bereits einsehbar - selbst entwickeln

(diese "Routenplanung" lässt sich dann später mit gesunden Erfolgserlebnissen sukzessive abhaken).

So gesehen ist es sogar ein Vorteil,

dass die 11. Klasse einen gewissen Freiraum vor dem teilweise gnadenlosen Stoffdruck der "eigentlichen" Oberstufe bietet: man sollte ihn weidlich nutzen!

2. im analytischen Teil der 11. Klasse spielt (vor der Einführung in die Differentialrechnung) der funktionale Zusammenhang die entscheidende Rolle.

Die Mathe-Richtlinien NRW weisen insbesondere auf einige zentrale mathematische "Ideen" hin, u.a. eben auf die

"Idee des funktionalen Zusammenhangs

Durch Funktionen werden Zusammenhänge erfasst, beschrieben und quantifiziert sowie Veränderungen handhabbar gemacht. Die Idee des funktionalen Zusammenhangs ist für die Mathematik von großer Tragweite und für das Verständnis der kulturellen Rolle der Mathematik unentbehrlich. Naturgesetze sind ohne die Formulierung funktionaler Zusammenhänge nicht denkbar. Ohne ein Begreifen der Idee des funktionalen Zusammenhangs lässt sich keine tiefere Einsicht in den wissenschaftlichen Fortschritt gewinnen. Aber nicht nur die Naturwissenschaften, sondern auch viele sozial- und humanwissenschaftliche Disziplinen machen zunehmend von der Möglichkeit Gebrauch, empirische Zusammenhänge durch Funktionen quantitativ zu beschreiben.

Weite Teile der ["eigentlichen", späteren] Oberstufenmathematik befassen sich mit Funktionen: Mit Mitteln der Differentialrechnung werden änderungen analysiert und die charakteristischen Merkmale von Funktionen ermittelt. In der Integralrechnung werden die Wirkungen fortgesetzter änderungen untersucht. Auch in der Geometrie wird der Funktionsbegriff wirksam. Abbildungen sind Funktionen. Bewegungen, durch Matrizen vermittelt, können als Funktionen aufgefasst und gedeutet werden. Verteilungs- und Dichtefunktionen spielen in der Stochastik eine bedeutende Rolle. Die Untersuchung des Funktionsbegriffs selbst kann an geeigneten Stellen für die Theorieentwicklung von Bedeutung sein.

Die Idee des funktionalen Zusammenhangs eröffnet den Schülerinnen und Schülern ein mächtiges Werkzeug, das ihnen helfen kann, mathematische Beziehungen in ihrer Alltagswelt aufzuspüren und diese dadurch besser zu durchschauen."
(S. 9)

Die hier angedachte Lerneinheit folgt ausdrücklich nicht einem Lehrbuch, also z.B.

1. Koordinatengeometrie - Geraden

1. Geraden im Koordinatensystem, lineare Funktionen

2. Bestimmung von Geradengleichungen

3. Lage zweier Geraden und Schnittwinkel zweier Geraden

4. Vermischte Aufgaben

Mathematische Exkursionen

Koordinatensysteme in der Landvermessung Rückblick 20

Aufgaben zum Üben und Wiederholen

2. Koordinatengeometrie mit Kreisen und Parabeln

1. Länge und Mittelpunkt einer Strecke

2. Kreise im Koordinatensystem

3. Kreise und Geraden

4. Parabeln im Koordinatensystem

5. Parabeln und Geraden

6. Parabeln und quadratische Funktionen

7. Vermischte Aufgaben

Mathematische Exkursionen

Kann das Spiegelbild einer Geraden krumm sein?

Rückblick

Aufgaben zum Üben und Wiederholen

    [...]

4. Funktionen

1. Stückweise lineare Funktionen, Betragsfunktion Potenzfunktionen

2. Ganzrationale Funktionen

3. Gerade und ungerade Funktionen, Symmetrie

4. Nullstellen ganzrationaler Funktionen

5. Vermischte Aufgaben

Mathematische Exkursionen

Zur historischen Entwicklung des Funktionsbegriffs

HORNER-Schema und Tabellenkalkulation

Rückblick

Aufgaben zum Üben und Wiederholen

    (zitiert nach: Lambacher Schweizer 11, Ausgabe Nordrhein-Westfalen)

Der zentrale Nachteil solcher eher noch Lehr- als Lernbücher

(Schulbücher geben eher der Lehrkraft Tipps, an was zu denken ist und in welcher Reihenfolge man es machen könnte)

 ist nämlich, dass in ihnen alles, und zwar

• sowohl inhaltlich

• als auch die (lineare) Anordnung,

fix und fertig vorgegeben ist, so dass nur noch partielle Abweichungen (und dann auch wohl nur durch die Lehrkraft) möglich sind

(z.B. schiebt o.g. Buch ein Kapitel "III Beschreibende Statistik" zwischen die beiden analytischen Kapitel "II Koordinatengeometrie mit Kreisen" und "IV Funktionen"; dem kann man - jeweils mit guten Gründen - folgen [also die Themen abwechseln] oder aber erst Analysis und dann Statistik betreiben;
ich vermute, dass die BuchautorInnen die oftmals ungeliebte Statistik vorgezogen haben, damit sie nicht - wie oftmals üblich - nach der gesamten Analysis inkl. Differentialrechnung am Ende des Schuljahrs "hinten runter fällt", also gar nicht mehr erledigt bzw. "auf die lange Bank" [immer das nächste Schuljahr] geschoben wird).

Der entscheidende (oder bei linearen Büchern unvermeidbare?) Fehler von Schulbüchern ist, dass sie

• eine fertige Mathematik vorgeben, die (was nur grenzenlos langweilig sein kann) nur noch "wiedergekäut" werden kann,

• und damit auch ein falsches Bild von dem, was Mathematik ist, erzeugen und über die Jahre hinweg immer mehr verhärten.

(vgl. )

Solch ein Vorgehen wie im o.g. Buch hat aber auch prinzipielle Nachteile:

• die SchülerInnen werden sozusagen für dumm verkauft, wenn wieder bei Adam & Eva angefangen und das Rad zum wiederholten Male neu erfunden wird, nämlich Geraden und Parabeln
  (auch wenn das Altbekannte immerhin mit neuen Aspekte [Schnittwinkel und Kreisgleichungen] garniert wird);

• die oben als so bedeutsam herausgestellte "Idee des funktionalen Zusammenhangs" geht verloren bzw. wird zu lange (bis in Kapitel IV) hinaus geschoben.

Mein Vorschlag ist daher, die gesamte Unterrichtseinheit unter den Oberbegriff "funktionale Zusammenhänge" zu stellen und dementsprechend Geraden und Parabeln nur als Teilaspekte zu betrachten:

Statt an Wiederkäuen von Altbekanntem bzw. (durch ein Buch) Vorgegebenem denke ich eher an .

Basistext für alles Folgende ist , also ein Text, der "mit aller Gewalt" zu veranschaulichen versucht und auch schon eine Reihenfolge als sinnvoll vorschlägt.

Aber

1. müsste diese Reihenfolge überhaupt erst (im Folgenden ansatzweise) erarbeitet (statt eben nur vorgegeben) werden,

2. werden im Text "Zuordnungen, Funktionen und Funktionenscharen" nur fertige Beispiele gegeben, die herzuleiten und zu begründen wären

(z.B.: wie ergibt sich die Sinusfunktion und warum ist sie periodisch? Bzw. wenn man den Sinusgraphen erst entdecken lässt, wird ja auch die Periodizität erst entdeckt).

Der Text  sollte also erst am Ende des Lehrgangs stehen, und zwar aufgefüllt durch Begründungen und auch Rechnungen

(z.B.: wie berechnet man denn den Scheitelpunkt einer Parabel?).

Der Text "Zuordnungen, Funktionen und Funktionenscharen" deutet aber auch schon an, welche Spezialaufgaben an Gruppen vergeben werden könnten, nämlich z.B. jeweils die Untersuchung eines Funktionentyps oder aber die Behandlung grundsätzlicher Probleme (z.B. "unterschiedliche »Zuordnungsmaschinen«").

Der Oberbegriff "funktionale Zusammenhänge" wird vorweg in drei relativ autonome Teilgebiete zerlegt

(die natürlich später zu verbinden bzw. zu "vernetzen" sind):

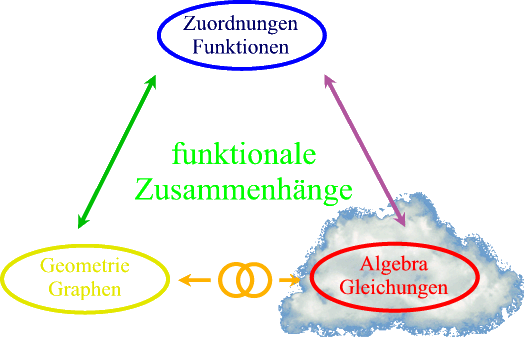
Die Wolke

(abgehoben, "über den Wolken", Wolkenkuckucksheim)

rechts unten soll dabei symbolisieren, dass erst da (beim Rechnen) Mathematik im eigentlichen Sinne betrieben wird

(wenn man mal klischeehalber davon ausgeht, dass reine Geometrie "eigentlich gar keine richtige Mathematik ist": eine Geringschätzung schon seit dem 19. Jahrhundert, der ich mich nicht anschließen möchte - und gegen die schon kein Geringerer als David Hilbert und Stephan Cohn-Vossen in ihrem Buch "Anschauliche Geometrie" angehen wollten).

Nichts gegen die algebraische Möglichkeit, Funktionen zu "erfassen". Aber sie scheint mir doch in Schulen allzu überbetont zu werden und damit das Grundverständnis dessen, was überhaupt eine Funktion bzw. ein "funktionaler Zusammenhang" ist, zu verbauen. Vor aller Algebra muss doch eine anschauliche Vorstellung von Funktionen geschaffen werden - und die Algebra muss viel deutlicher andauernd darauf rückbezogen werden:

1. Zuordnungen/Funktionen als Tätigkeit:

dass (in der Mathematik) nur Zahlen einander zugeordnet werden, ist doch ein sehr später Schritt:

vorher sollten doch "Dinge" einander zugeordnet werden, und zwar am besten durch regelrechtes Schieben und Hin-Schleppen.

Man tue wirklich das Beispiel:

jedem Schüler werden die Stifte zugeordnet, die er zufällig gerade in der Hand hat:

• zuerst stehen alle SchülerInnen auf;

• wer gerade keinen Stift in der Hand hat, wird der Einfachheit halber aus der Betrachtung ("Definitionsmenge") ausgenommen (darf sich wieder setzen);

• wenn jemand zufällig gerade mit zwei Stiften rumhantiert, liegt keine Funktion mehr vor (und wird er deshalb aus der "Definitionsmenge" ausgenommen);

• wenn nun die verbleibenden (stehenden) SchülerInnen jeweils einen Stift in der Hand haben, liegt eine Funktion vor;

• die Zuordnung ist dann umkehrbar (also wieder eine Funktion), wenn es um den jeweils eigenen (z.B. mit einem Namenszettel versehenen) Stift geht;

• die Zuordnung ist dann nicht umkehrbar (also nicht mehr eine Funktion), wenn es um den Stifttyp geht (z.B. Stabilo point 88 fine 0,4 rot). Auch das tue man: man sammle alle (nicht mit Besitzernamen versehenen) Stifte ein, mische sie - und wird feststellen: da sind z.B. drei der eben genannten Stifte drunter, und da sie äußerlich ununterscheidbar sind,  ist nicht mehr klar, wem sie gehören.

Man nehme vorweg massenhaft solche Beispiele aus allen nur denkbaren Lebensbereichen durch - und tue sie.

Ein späterer Schritt besteht dann darin, "Dinge" einander zuzuordnen, die schon mit Zahlen verbunden, aber eben noch nicht nur Zahlen sind:

•                             SchülerInnen |→ Schuhgröße (in Zahlen)

• durchnummerierte SchülerInnen |→ Schuhgröße (in Zahlen)

Wichtig schon hier (vor aller Mathematik und Rechnung) ist :

• allgemeine Zuordnung/Spezialfall

  • 

  • 

  • 

2. Geometrie/Graphen:

Hier gibt es zwei Möglichkeiten:

1. Zuordnungen aus 1. werden zu visualisieren versucht. Sinnvoll sind da insbesondere Zuordnungen, die man ohne Graph überhaupt nicht oder nur schwerlich "überblicken" kann (unsortiert wirkende Listen, deren Bildungsgesetz bzw. "Dramatik" allein aufgrund der Zahlen noch nicht klar wird).

2. Es werden fertige Graphen (etwa aus Zeitschriften) vorgegeben und beschrieben.

(Wichtig scheint mir auch, das kartesische Koordinatensystem überhaupt erst wieder zu entdecken oder zumindest doch zu würdigen [erst später auch im Hinblick auf die algebraische Beschreibbarkeit]; vgl. ).)

Die Beschreibung erfolgt hier noch ohne jegliche Zahlen und Algebra, ja am besten tut man sie wieder: da es aber schwierig sein wird, z.B. eine Achterbahn ins Klassenzimmer zu bringen, fahre man eine Kurve immerhin mit einem Spielzeugauto ab

(mit echtem Steuerrad, so dass man z.B. eine Links- oder Rechtskurve wirklich tut und sieht:

).

Rein deskriptiv lassen sich hier schon bekannte und unbekannte (Zukunftsprogramm) Sachverhalte herausarbeiten:

• Schnittpunkt mit der y-Achse (und seine Bedeutung etwa bei den Finanzen einer Firma),

• Nullstellen,

• Minima und Maxima,

• Links- und Rechtskurve,

• Wendepunkte (Sattelpunkte),

• Stetigkeit,

• Differenzierbarkeit

• ...

Geeignete Modelle sind da etwa

• die Finanzen einer Firma,

• eine Bergwanderung im Nebel, bei der man (von links nach rechts gehend) immer nur ein kurzes Stück vorausschauen kann.

Beide haben den Vorteil, dass die Kurve eine dramatische, weil noch offene Geschichte erzählt, nämlich z.B.:

• "ein Maximum (der Firmengewinne) ist eigentlich kein Grund zu feiern ("zu früh gefreut!"), sondern danach geht es ja wieder bergab",

• "bei einem Wendepunkt schwächt sich z.B. der (zwar noch anhaltende) Abwärtstrend immerhin schon ab (erster Anlass für einen verhaltenen Optimismus)",

• "eine noch sanfte Linkskurve beim Aufstieg auf einen Berg ist eine leider oft sträflich übersehene oder verharmloste deutliche Warnung: es wird zunehmend steiler, und bald könnte die senkrechte Eiger-Nordwand vor uns stehen; wäre es da - im Nebel - nicht besser, rechtzeitig umzukehren?"

Solch "dramatische" Betrachtungen sollten später (insbesondere in 3.) auch immer wieder bei rein mathematischen Funktionsgraphen erfolgen

("angenommen, der Sinusgraph ist eine wellenförmige Landschaft aus Bergen und Tälern ...").

2. Algebra/Gleichungen:

Hier müssten insbesondere erarbeitet werden
(vgl. jeweils ):

• y =

•  

  x rein →

  → y raus

• allgemeine Regel

• Spezialfall          

• grundsätzliche Details
  (Nullstellen N (x | 0), Schnittpunkte mit der y-Achse S_y (0 | y) ...; vgl. auch ),

• die Möglichkeit, dass eine Funktionsgleichung viele Anwendungsfälle "erfasst"
  (völlig unterschiedliche Aufgabenstellungen, die auf dieselbe Funktionsgleichung hinauslaufen),

• Gemeinsamkeiten und Unterschiede innerhalb und zwischen Funktionstypen.

Wichtig sind aber vor allem die Verbindungspfeile der drei "Eckdaten" bzw. Teilthemen, und zwar insbesondere die erstrebteHochzeit von Geometrie und Algebra fast als Grundmovens der gesamten Schulmathematik und ihrer "Dramaturgie" über die Schuljahre hinweg (und eigentliche Genietat von Descartes):

"wir (?) wollen (?) alles zeichnen können, was wir berechnen können und - viel schwieriger - umgekehrt"

(das sollte sich dann - nebenbei - auch in mehr und mehr zusammenlaufenden Fäden im  "Wissensnetz" zeigen)

Oben war schon deutlich geworden, wie die reine Graphenbeschreibung mit

• Schnittpunkt mit der y-Achse (und seine Bedeutung etwa bei den Finanzen einer Firma),

• Nullstellen,

• Minima und Maxima,

• Links- und Rechtskurve,

• Wendepunkte (Sattelpunkte),

• Stetigkeit,

• Differenzierbarkeit

• ...

schon ein algebraisches Programm nahelegt.

Umgekehrt sollte aber auch jedes algebraische Ergebnis am zugehörigen Graphen gemessen werden:

• welches rechnerische Ergebnis ist (vor aller Rechnung) vom Graphen ausgehend möglich und erwartbar?

• kann ein rechnerisches Ergebnis (am Graphen gemessen) stimmen?

• was bedeutet ein rechnerisches Ergebnis in graphischer Hinsicht?

"Vom Graphen ausgehend" heißt für mich auch, dass

• nicht mit Funktionsgleichungen angefangen wird, zu denen beispielsweise die Nullstellen gesucht werden,

• sondern umgekehrt von Nullstellen, zu denen erst eine passende Funktionsgleichung gesucht wird.

Die Schülergruppen werden ermutigt, so anschaulich wie nur irgend möglich zu arbeiten

(vgl. wieder ):

• leuchtendes Vorbild sind da die technischen Erklärungen in "Die Sendung mit der Maus"

•  

(Jesus und der ungläubige Thomas)

"Glaubt nichts, was ihr nicht gesehen und berührt habt!"

Die SchülerInnen sollen also

• am besten Dinge tun:

(z.B.

• wirklich strecken und stauchen:

)

• Modelle bauen
  (vgl. ),

• im Internet Computerprogramme und Animationen suchen

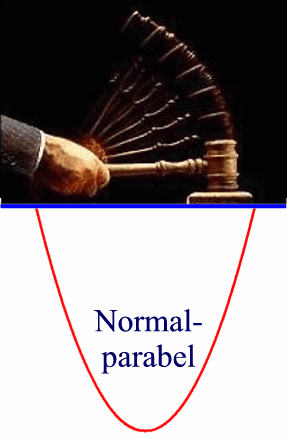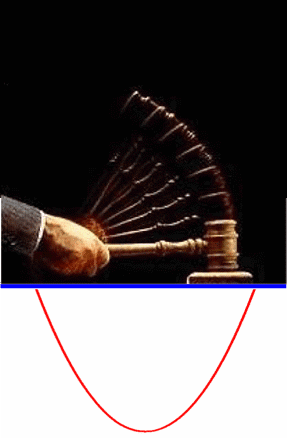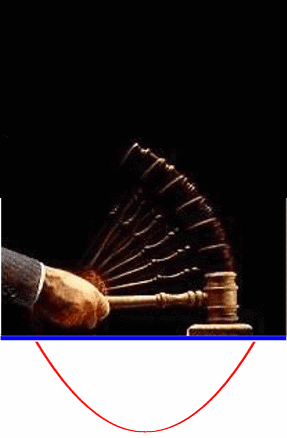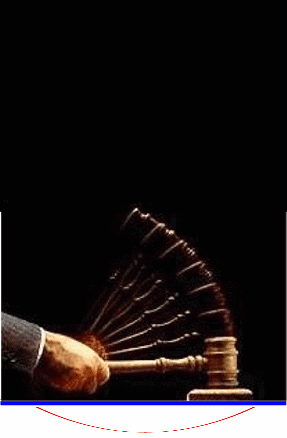
(z.B. ),

• andere FachkollegInnen ansprechen

(z.B. "Wellenmaschinen" in der Physik )

(Nochmals: die Anschaulichkeit soll natürlich nicht die Rechnungen ersetzen, sondern sie vorbereiten; und umgekehrt sollen Rechenergebnisse nachträglich wieder veranschaulicht werden.)

Vgl. auch die zugehörige Klausur.