Rasterfahndung
| | Rasterfahndung "computergestützte Suche in außerpolizeilichen Datenbeständen nach einem noch unbekannten Täter" in Berlin z.B. nach folgenden Kriterien: -
männlich -
islamische Religionszugehörigkeit ohne nach außen tretende fundamentalistische Grundhaltung -
legaler Aufenthalt in Deutschland -
keine eigenen Kinder -
Studientätigkeit (technische Studienfächer) -
Mehrsprachigkeit -
Keine Auffälligkeiten im allgemeinkriminellen Bereich -
rege Reisetätigkeit -
häufige Visabeantragungen - finanziell unabhängig
- Flugausbildung.
(zitiert nach  ) ) |
Weil es gilt, mit allen nur erdenklichen Mitteln zugunsten des mathematischen Verständnisses anschaulich zu werden, Bilder über Bilder:
SchülerInnen müssen - und zwar in dieser Reihenfolge -

(hier die typische Diagonale in vielen Bildern)

Bzw. SchülerInnen müssen den richtigen "Polarisationsfilter" parat haben und herausfinden, mit dem zentrale Aspekte besonders deutlich hervortreten.
Mathematik ist laut David Hilbert ganz wesentlich eine Wissenschaft der Strukturen (also von etwas geradezu "Metaphysischem" zwischen den Dingen).
Hier kann nicht genauer dargestellt werden, was Hilbert genau unter "Strukturen" verstand ("formale Systeme"), sondern wir biegen es uns für unsere Zwecke hin:
-
der Aufbau bestimmter mathematischer Gebiete oder auch der Gesamtmathematik,
-
Denkstrukturen/typische Herangehensweisen (z.B. auch Beweisstrukturen),
-
Analogien zwischen verschiedenen mathematischen Gebieten,
-
optische Strukturen,
und um letztere soll es mir hier gehen.
Das Problem, dass SchülerInnen bei (Standard-)Aufgaben oftmals "wie der Ochs vorm Berge" stehen und nicht mal sagen können, worin ihre (Einzel-)Schwierigkeiten bestehen
(um von ihnen ausgehend nach [Teil-]Lösungen und dann sukzessive nach der Gesamtlösung zu suchen),
liegt vielleicht vor allem darin begründet, dass sie
-
sichschlichtweg (aus mehr oder minder gutem Grund) nicht dafür interessieren und entsprechend "lieblos" drangehen,
-
von Anfang an vor der Fülle der Schwierigkeiten resignieren und daher meinen, beim Drauflosrechnen vielleicht immerhin "versehentlich" einige Punkte "abzocken" zu können
("es wird ja hoffentlich nicht alles falsch sein")
-
sofort losrechnen und alle Probleme gleichzeitig lösen wollen
(manchmal auch, weil sie sich zu viel zutrauen und Zwischenschritte für schnöde halten),
-
sie die "Dinge" (z.B. monströse Terme) nicht unter ein Raster legen.
Ein Beispiel:
Im Lambacher Schweizer 10
(Mathematisches Unterrichtswerk für das Gymnasium; Ausgabe Nordrhein-Westfalen; Ernst Klett Verlag)
steht auf S. 72 an prominenter Stelle (Rand) und besonders fett gedruckt folgende Aufgabe:
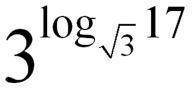 = ?
= ?
(wobei hier nicht über Sinn und Unsinn solcher Aufgaben diskutiert, also auch nicht die leidige Diskussion zu Termumformungen wieder aufgewärmt werden soll).
Die Botschaft ist klar: "Ich bin eine besondere Herausforderung, und deshalb (er-)löse mich!"
(Manchmal fragt man sich, ob mit solchen Aufgaben nicht die besonders leistungsstarken, sondern die besonders stumpfen SchülerInnen herausgefordert werden.)
EinE mittelprächtigeR SchülerIn wird da natürlich sofort sagen: "Jetzt erst recht nicht (freiwillig)."
Worin denn nun liegt die Schwierigkeit dieser Aufgabe?:
Erstmal doch vor allem darin, dass da alle nur denkbaren "Schweinereien" vereinigt sind:
-
auch nicht von Pappe: eine eklige Wurzel,
-
der derzeitige Unterrichtsstoff, also ein Logarithmus
(und der ist nun wirklich igitt, weil scheußlich um die Ecke gedacht),
-
dann auch noch der Logarithmus der schäbigen Zahl 17
(während man die glatt aufgehenden Zweier- und Zehnerlogarithmen ja vielleicht noch beherrschen ["rauskriegen"] würde),
-
und um das Fass zum Überlaufen zu bringen, der widerliche Logarithmus nicht hübsch alleine, sondern sogar noch im Exponenten
(womit immerhin schon die zentrale Erkenntnis eingetreten wäre).
Der wichtigste, gleichzeitig aber selbstverständlichste
(weil im direkten Bezug zum derzeitigen Unterrichtsstoff stehende)
"Wink mit dem Zaunpfahl" ist da noch "Logarithmus".
Es wird da also wohl (mindestens) eins der vertrackten Logarithmengesetze anzuwenden sein. Nur welches?
(wenn man sie überhaupt [alle] behalten hat)
Genau hier kommt die "Struktur" ins Spiel, und zwar im doppelten Sinne:
-
nicht bloß das pure Auswendiglernen und Runterrattern, sondern das Wissen, wann genau ein Logarithmengesetz gilt - und wann nicht.
Beispielsweise (das werden wir unten noch brauchen) gilt
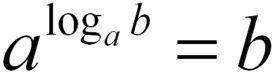
(und fällt also das a komplett raus!)
dann und nur dann, wenn in der Basis beidesmal (dasselbe!) a steht.
(Nur nebenbei erwähnt sei, dass die Gleichung ja gerade die Quintessenz der Umkehrfunktion ist.)
Um dieses "beidesmal (dasselbe!)" suggestiver zu machen, müsste man vielleicht folgendermaßen "sprechen":
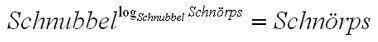
Ist doch herzhaft egal, was da jeweils steht
(wobei hier solche Feinheiten wie der Definitionsbereich mal weggelassen seien),
ja, es kann sogar sowas Ekliges wie eine Wurzel (s.o.) sein,
Hauptsache, es steht da an entsprechenden Stellen jeweils DASSELBE.
(Nebenbei: man sollte natürlich auch jene Fälle durchnehmen - und das wird mit o.g. Anfangsaufgabe ja auch gemacht -, in denen
-
an entsprechenden Stellen nicht dasselbe bzw. - erst recht hinterhältig - nur verführerisch ähnliches steht,
-
die Zahlen vertauscht sind, das Gesetz also nicht mehr gilt
[und warum es dann nicht mehr gilt]:
 )
)
Oder vielleicht noch suggestiver:

Oder um den den wichtigen Effekt klarzumachen, dass dieses Gesetz etwas Unliebsames
(z.B. eine zweite Variable, die oftmals zur Unlösbarkeit führt)
verschwinden lässt, könnte man folgendermaßen illustrieren:
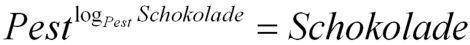
Wer wollte nicht sowas höchst Unangenehmes wie die Pest loswerden und nur die ach so wohlschmeckende Schokolade behalten
(wobei auch intuitiv klar wird, dass man Pest und Schokolade bittschön nicht verwechsle)?!
- Fast (in unserem Falle) noch wichtiger an
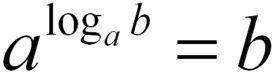
ist aber, dass es das einzige Logarithmengesetz ist, welches von einem Logarithmus im Exponenten handelt.
Auch das gälte es besonders anschaulich zu machen, und zwar z.B. durch ein ganz simples Raster (!), das die Grundform verdeutlicht:

(Für die anderen Logarithmengesetze wären entsprechende Raster anzufertigen.)
Jetzt aber wird sehr viel deutlicher, dass nur dieses Raster auf o.g. Anfangsaufgabe passt:

(Nebenbei: was ich hier - von wegen zweidimensionalem Bildschirm - durch Farben klar gemacht habe, würde ich "im wirklichen Leben" durch echte, mechanische und anfassbare Raster bzw. mit Schablonen klar machen, in die der Term wortwörtlich reinpasst:

Und entsprechende Raster gäb´s auch für simplere Termumformungen, also z.B. die Binomis. Klammern z.B. vermittle man mit Schachteln, die man auch nur ineinander setzen kann, sich aber nicht überlappen können. Und natürlich packt man eine Schachtel nach der anderen aus.)
Es bleibt natürlich das Problem, dass das Raster nicht ganz passt, weil eben (vgl. 2.) nur annähernd dieselben Basen vorliegen. Hier nun muss die Überlegung in Gang kommen, dass in den Basen beidesmal exakt dasselbe stehen muss, also
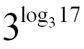
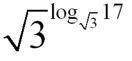
Und mit diesem zweiten Fall ist man dann tatsächlich nah an der Lösung, indem man eingedenk des Zusammenhangs von 3 und 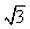 umschreibt:
umschreibt:
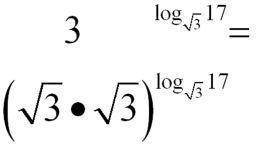 ,
,
woraus sich mittels (im Vergleich mit den Logarithmengesetzen) einfachem Potenzgesetz ergibt:
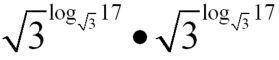
Auf jeden der beiden Faktoren passt nun ENDLICH vollständig das Logarithmengesetz 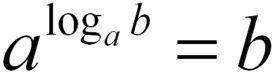 , so dass sich ergibt:
, so dass sich ergibt:
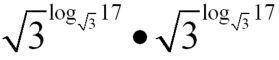 =
=
17 ● 17 =
289
| PS: | Es erweist sich mal wieder: -
braucht man eine enorme Menge strukturierten (Vor-)Wissens, um diese Aufgabe lösen zu können
(man muss schon betriebsblind sein, um das alles für selbstverständlich zu halten), -
lieben MathematiklehrerInnen fatal Aufgaben, die anfangs ganz schrecklich (abschreckend?!) schwierig aussehen und bei denen am Ende was ganz (beschämend?!) Einfaches rauskommt
(was immerhin auch - in der typischen Mathematikunterrichtslogik - ein Hinweis darauf ist, dass das Ergebnis richtig ist). |


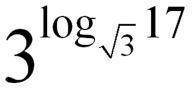 = ?
= ?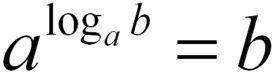




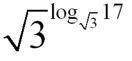
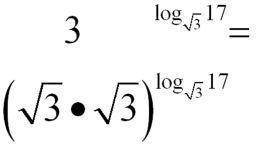 ,
,