(angeleitetes) Selbstentdecken?

Es ist eine (unten noch genauer behandelte) Banalität, dass SchülerInnen nicht alles selbst entdecken können und müssen. Nur befürchte ich, dass im Gegenzug allzu leicht vorausgesetzt wird, dass SchülerInnen eigentlich gar nichts selbst entdecken können.

Bzw. das Selbstentdecken wird als purer Zufall hingenommen

(einige wenige "bessere" SchülerInnen werden vielleicht drauf kommen; wenn aber nicht, so bringe ich [der Lehrer] das Neue ein),

statt dass man es immerhin mal zu initiieren versucht.

Ich werde den Verdacht nicht los, dass man da nur seine eigene "Sattheit" projiziert: man weiß ja längst, wies geht, denkt also nur noch von den fertigen Ergebnissen aus, und kann sich daher beim besten Willen nicht mehr vorstellen, wie man selbst drauf kommen kann.

Bemerkenswert ist auch, dass von "selbstentdeckendem Lernen" fast ausschließlich in der (ach so einfachen?) Grundschulmathematik die Rede ist. Für die Zeit danach scheint man völlig resigniert zu sein.

Schon in "Thesen und Fragen" war das Problem aufgeworfen worden,

• was denn nun eigentlich "Selbstlernen" sei,

• welche verschiedenen Formen es haben könnte,

• inwieweit Selbstentdecken dazu gehöre,

• ob Selbstentdecken bei der Komplexität und Fülle des Stoffs überhaupt eine realistische Möglichkeit sei.

Es ist allemal klar, dass SchülerInnen (und LehrerInnen wohl auch) völlig überfordert wären, wenn sie

1. die gesamte Mathematikgeschichte (oder genauer: die des Schulstoffs) innerhalb weniger Schuljahre und

2. die Erkenntnisse großer Genies

völlig selbstständig (nach-)entdecken sollten.

Wenn die Forderung nach völlig selbstentdeckendem Unterricht gestellt würde, wäre damit auch gleichzeitig der völlige Rückzug der Lehrkraft gemeint: "Jetzt entdeckt mal schön selbst." Vordergründig wäre das eine "Demokratisierung" des Unterrichts, in Wirklichkeit aber nur ein Alleinlassen der SchülerInnen.

Wenn überhaupt, so ist Selbstentdecken

1. nur immer mal wieder (an besonders wichtigen Stellen?) und exemplarisch möglich;

2. bedarf es einer Anleitung, die immerhin die Fiktion des Selbstentdeckens herstellt.

Der erste Knackpunkt dabei ist: Wie erreicht man diese Fiktion, ohne nur suggestiv zu verfahren und  schon allzu viel vorzugeben?

Und der zweite, viel problematischere Knackpunkt ist: Wie kann das an einem konkreten Beispiel aussehen (statt nur Sonntagspredigt zu bleiben)?

Im folgenden soll an einem eher beliebigen Beispiel aus meiner derzeitigen Unterrichtspraxis der erste Versuch solch einer Konkretisierung gemacht werden.

Angenommen, die SchülerInnen sollen die Besonderheiten derjenigen kubischen Funktionen herausfinden, die nur ungerade Exponenten enthalten. D.h. sie sollen entdecken, dass (nur) die Graphen dieser kubischen Funktionen symmetrisch zum Ursprung sind.

Gibt es eine programmtechnische Möglichkeit, die SchülerInnen zu einer Entdeckung der Symmetrie anzuleiten?

(Das Problem ist ja, dass viele Programme [vgl. etwa , neuerdings aber auch vermehrt java-applets] "nur" visualisieren, was bereits entdeckt ist. Das ist zweifelsohne auch wichtig, nur hier nicht gewollt.)

Ein Programmiervorschlag:

• Voraussetzung: Der Umgang mit Funktionen dritten Grades ist schon gefestigt (Aussehen, Nullstellen ...).

• Ein Funktionsgraph dritten Grades, also z.B.

,

ist frei über ein Koordinatensystem verschiebbar, wobei immer auch die zugehörige Funktionsgleichung angezeigt wird
(selbstverständlich liegt der Wendepunkt des Funktionsgraphen anfangs nicht im Ursprung, weil damit ja alle Erkenntnis vorweg genommen würde - und eben gerade deswegen nicht zustande kommen könnte?)

• Die Quadranten des Koordinatensystems sind verschieden eingefärbt, wobei der 1. und 3. bzw. 2. und 4. Quadrant jeweils in Komplementärfarben erscheinen, also z.B.

• Das Funktionsgraphenstück, das über einem bestimmten Quadranten liegt, erscheint wiederum in dessen Komplementärfarbe. Z.B.
  erscheint ein Funktionsgraphstück, das über dem ersten, blauen Quadranten liegt, in dessen Komplementärfarbe gelb - also der Farbe des dritten Quadranten:

Die alles entscheidende Frage ist nun, ob die SchülerInnen dadurch angeleitet werden, den Graphen solange zu verschieben, bis

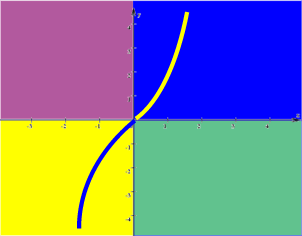
erscheint - ohne dass das Ergebnis schon suggestiv induziert wird.

Zusätzlich wird noch die jeweilige Funktionsgleichung angezeigt.

Die Aufgabenstellung hieße also völlig offen z.B.: "Verschiebe den Graphen und achte auf besondere Effekte sowie die jeweilige Funktionsgleichung."

Sei es, weil

• Begriff und Inhalt des Wendepunktes noch gar nicht bekannt sind,

• dieser im Programm bewusst nicht auf dem Graphen markiert ist:

die SchülerInnen könnten

• Schwierigkeiten haben, die sich andeutende Symmetrie des Graphen zum Ursprung allein durch Verschieben exakt zu erreichen,

• aber bemerkt haben, dass der Koeffizient vor dem quadratischen Term gegen Null geht, und diesen dann in der Funktionsgleichung manuell auf Null setzen - womit sie die entscheidende Entdeckung gemacht hätten.

Es ist wäre zu fragen, ob solch ein Programm (wenn es denn überhaupt zum gewünschten Ergebnis führen würde) schon die beabsichtigte Erkenntnis vorweg nähme. Mir scheint: Nein, weil nur die Quadranten und Graphenstückfarben vorgegeben werden, nirgends aber die Symmetrie.

Und dennoch wurde wohl in zweierlei Hinsicht "gemogelt":

1. sticht der Ursprung, um den es ja zentral geht, durch die Farbgebung noch mehr hervor als sowieso schon im Koordinatensystem bzw. Unterricht; allerdings ist ja üblicherweise noch nicht der Wendepunkt durchgenommen (oder zumindest noch nicht im vorliegenden Zusammenhang erwähnt), der in den Ursprung verschoben werden muss;

2. durch die Komplementärfarben der Funktions"zweige": Wenn nämlich der Graph "richtig" - d.h. mit dem Wendepunkt im Ursprung - positioniert ist, suggerieren schon allein die Komplementärfarben die Symmetrie.)

Weiterhin wäre zu fragen, welche Position das Programm in einer Unterrichtseinheit haben sollte:

• War die allgemeine Symmetrie schon vorher erarbeitet worden und fällt sie jetzt nun nur noch auf die zum Ursprung zurück?
  (Links-/Rechtskurven sowie Wendepunkt kann man ja anschaulich durchaus schon in der Mittelstufe durchnehmen, wenn auch noch nicht berechen; womit allerdings schon ein interessanter Vorverweis auf die Oberstufe möglich ist [wo kommen wir her, wo wollen wir hin?])

• War die Symmetrie überhaupt noch nicht Thema und wird jetzt erst anhand der Symmetrie zum Ursprung entdeckt und von da aus rückwärts für alle anderen Funktionsgraphen (während des Verschiebens) rückgeschlossen?

• Selbstverständlich darf es nicht beim reinen (vom Computer generierten) Effekt bleiben, sondern im Folgenden müsste natürlich untersucht werden, warum (nur) Funktionen mit rein ungeraden Exponenten symmetrisch zum Ursprung sind.

Es sei dahin gestellt, ob das hier angedachte Programm das Gütesiegel "angeleitetes Selbstentdecken" verdient.