![]() Vorwort
Vorwort
![]() Modelle
Modelle
![]() Vortrags-
und Workshop-Angebote
Vortrags-
und Workshop-Angebote
Vgl.


(![]() , 29.8.15)
, 29.8.15)
 |
"One of the saddest developments in school
mathematics has been the downgrading of the visual for the
formal." (Ian Stewart) |
|
 |
"Sind
Formeln denn nicht nur rigide Denkkrücken oder
Verständigungsformen für Mathematiker, die sich so ihre
inneren Bilder gegenseitig mitteilen? Was ist Mathematik? Die
Idee? Oder der Beweis? Die Formel? Oder das Bild?" (Gunter Dueck) |
|
"In der Überzeugung, dass manche von uns sich nicht mit
der Mathematik einlassen, weil wir sie nicht sehen können,
setzt Professor Frenkel sie [in  ] unermüdlich in Beziehung zu
Dingen, die wir sehen können." ] unermüdlich in Beziehung zu
Dingen, die wir sehen können."(The Guardian) |
||
 |
"Der
Mensch ist ein Augentier, das stimmt, aber mit einem
Gegenstand wirklich vertraut wird er doch erst, wenn er ihn in
die Hand nehmen oder zumindest um ihn herumlaufen kann." (Ulf von Rauchhaupt) Und sogar Roboter lernen besser, wenn sie um die Dinge herumgehen, sie sich von allen Seiten ansehen - und sie anfassen. Vgl.  |
|
 |
"[...] tun wesentliche Teile der Großhirnrinde beim Menschen
nichts anderes, als Modelle zu erzeugen, Modelle über die Umgebung
und über uns selbst." (Ulrich Eberl) |
|
 |
"Die
Abgründe der Ahndung, ein sicheres Anschauen der Gegenwart,
mathematische Tiefe, physische Genauigkeit, Höhe der Vernunft,
Schärfe des Verstandes, bewegliche, sehnsuchtsvolle Phantasie,
liebevolle Freude am Sinnlichen, nichts kann entbehrt werden zum
lebhaften fruchtbaren Ergreifen des Augenblicks, wodurch ganz
allein ein Kunstwerk [...] entstehen kann." (Johann Wolfgang Goethe) |
|
 |
 ( |
|
|
|
-
Vor schätzungsweise 20 Jahren habe ich ein Bündel von Matheprogrammen mit dem Titel
 Bewegte Mathematik
geschrieben, bin danach aber - in Gegenrichtung zum Zeitgeist - zu
mechanischen 3D-Modellen fortgeschritten.
Bewegte Mathematik
geschrieben, bin danach aber - in Gegenrichtung zum Zeitgeist - zu
mechanischen 3D-Modellen fortgeschritten.
("Auf der A1 kommt Ihnen ein Geisterfahrer entgegen." "Einer? Hunderte!")
-
Eine ausgiebige Internetrecherche hat ergeben, dass ich anscheinend der Einzige bin, der Mathemodelle für alle Schulthemen baut. Ansonsten finde ich nämlich
(vor allem in uralten, verstaubten Sammlungen wie
z.B. ![]() ,
aber auch bei einschlägigen Lehrmittelanbieter)
,
aber auch bei einschlägigen Lehrmittelanbieter)
nur Modelle geometrischer Gegenstände und dreidimensionaler Funktionsgraphen.
Fast gar nicht finde ich aber bewegliche
Modelle (also ![]() Bewegte Mathematik), mit denen die Schüler selbst
hantieren können:
Bewegte Mathematik), mit denen die Schüler selbst
hantieren können:
(man achte mal drauf:
oft sind die Hände von Schülern schlauer als ihre Münder)
(samt Tourneen dieser Ausstellung kreuz und quer durch Deutschland) .
Es gibt allerdings zwei Unterschiede zwischen seinem und meinem Ansatz:
- sammelt er besonders schöne mathematische Objekte
(wohl, um überhaupt erstmal einen Zugang zur Mathematik zu zeigen) ,
während es mir weitgehend um eine Veranschaulichung von ordinärem Schulstoff und damit auch um "fundamentalere" mathematische Begriffe wie beispielsweise den der "Funktion" geht,
setzt er (zeitgemäß?) auf erstaunliche Effekte, während es mir in der Regel um Verständnis geht.
Ähnlich wie mit dem
steht es nebenbei mit dem

in New York, das zu besuchen ich nun (2019) Gelegenheit hatte.
("National Museum" finde ich aber arg dick aufgetragen für das, was dann da wirklich geliefert wird.)
-
Die meisten Menschen denken anschaulich, und das heißt mechanisch

(nicht zu verwechseln mit mechanistisch) ,
also anseh- und anfassbar:
"Geräte, die man nicht mit Lego® nachbauen kann, hat man nicht wirklich verstanden."
(anonym)Vgl.:
"Ich kann nur das verstehen, was ich auch erschaffen kann."
(Richard Feynman)
-
Gerade weil die "reine" Mathematik naturgemäß abstrakt ist, bedarf sie (zumindest in den Anfangsgründen) der materiellen "Eselsbrücken". Z.B. ist eine
1-Meter-
eben doch "was ganz anderes" als eine klitzekleine, zweidimensionale Abbildung einer Kugel in einem Schulbuch (oder hier im Text).
Und eben solche 1-Meter-Kugeln müssen in unsere Köpfe kommen:

(Max Goldt ist mal aufgefallen,
dass alle Innenstädte mit kugelförmiger "Kunst im öffentlichen Raum"
zugemüllt sind)
So ist mir manchmal danach, die Materialität (u.a. Handschmeichler) zu einem eigenen (Neben-)Thema im Mathematikunterricht zu machen:

Das gilt auch und gerade für industrielle perfekte Produkte, die ja bereits Abstraktionen sind:
früher war es gar nicht möglich, perfekte Kugeln herzustellen, heute hingegen sind die perfekten Kugeln identisch mit Platons "Ideen" - worüber man sich erst anhand großer Kugeln wundern kann.
-
Die Mathematik steht in einer wechselseitigen Beziehung zur "Außenwelt":

- einerseits ist die Mathematik erstaunlicherweise enorm erfolgreich auf die Außenwelt anwendbar
dem wird im Schulunterricht durch sogenannte "Anwendungsaufgaben" Rechnung getragen
und überhaupt interessieren mich Anwendungen reichlich wenig) ;
- andererseits
ist die Außenwelt ein unendliches Reservoire an Bildern und Vorgängen, die Innermathematisches veranschaulichen können.
Und ich wette, dass die allermeisten großen Mathematiker keineswegs so abstrakt, wie man oft annimmt, sondern in Bildern denken, und sie verstehen etwas erst wirklich, wenn es sich
zu einem Bild zusammensetzt.
Um so mehr brauchen Anfänger Veranschaulichungen
-
Ich glaube an den "Nährwert" von Metaphern:
man frage z.B. nur mal Schüler, wie ein Zylinder mit oben und unten angesetzten Halbkugeln aussieht - und dann erhält man so sicher wie das Amen in der Kirche die Antwort:
Für mich ist z.B.
eine Termumformung eine
,
das Lösen von Gleichungen eine
,
die Unbekannte x ein (?)
unter einer Tarnkappe, die ihm am Ende abgerissen wird,
der Sinus das Gestänge einer
.
(siehe zu allen vier Beispielen entsprechende Modelle bzw. Poster unten).
Für die ergiebigste mathematische Metapher halte ich aber die

-
Im Regelfall ist ein materielles Modell allemal besser als jedes immer nur virtuelle Computerprogramm
(überhaupt werden Computer und insbesondere sogenannte Grafische Taschenrechner im Hinblick auf den Mathematikunterricht gefährlich überschätzt) .
Gegen echte (!) Modelle spricht oftmals nur zweierlei:
der Aufwand ihrer Herstellung,
technische Grenzen der Modell-Mechanik beispielsweise bei Limesprozessen.
-
Vielleicht ist es im virtuellen Zeitalter nurmehr ein letztes Aufzucken rückwärtsgewandter Nostalgie, vielleicht aber auch eine wichtige Gegenbewegung, die Dinge wieder
zu wollen. Zumindest fällt mir seit einiger Zeit eine erstaunliche Rückkehr zur rostigen und damit eben nicht aalglatten Mechanik auf:




(... wobei allerdings bei drei der
vier gezeigten Beispiele die Mechanik
[wie auch das Rasen und Ballern in vielen Computerspielen]
virtuell bleibt - und das Ballern glücklicherweise.)
-
Es ist pädagogisch destruktiv, dass heutzutage alles glatt und perfekt ist

und andauernd sagt: "Sowas kriegst du nie hin, da brauchst du erst gar nicht anzufangen."

(wobei es mir auch um die Natur,
mindestens eben so sehr aber um das Schmuddelige [neudeutsch
"shabby chic"],
Nichtperfekte geht)
-
Die meisten meiner Modelle gäbe es am besten in Klassensatzstärke, so dass jeder Einzel- oder zumindest je zwei Schüler zusammen ein Modell hätte(n) und daran rumhantieren könnte(n).
Leider ist aber die Herstellung meiner Modelle oftmals derart aufwändig, dass meine Zeit nur für die Herstellung jeweils eines einzigen Modells reicht.
Immerhin sind die (Tafel-)Modelle dann aber aus zwei Gründen sehr groß:
-
, damit sie wie Ausstellungexponate "was her machen",
-
, damit ihre Details auch in der letzten Reihe gut sichtbar sind.
(Nebenbei:
-
Vergrößern kann Kunst sein, wenn es die Schönheit und Ingeniosität alltäglicher Gegenstände überhaupt erst [wieder] sichtbar macht.

-
viele meiner Modelle sind hinten mit Haken versehen, so dass man sie leicht an die Tafel hängen kann:

-
Nichtmathematiker, die die mathematischen Hintergründe meiner Modelle nicht kannten und denen diese auch herzhaft egal waren, fanden einige dieser Modelle "einfach schön", und ein Freund wollte eines meiner Mathemodelle sogar gerne als Wohnzimmerschmuck aufhängen:
[vgl. unten]
-
Bei meinen Modellen ergibt sich dasselbe Problem wie bei meinen Matheprogrammen
 Bewegte Mathematik: wenn man
sie zu früh einsetzt, wirken sie teilweise allzu suggestiv
(verraten schon alles) - und sind dann vermeintlich in wenigen
Sekunden erledigt. Vor allem rauben sie den Schülern, was überhaupt
erst Erkenntnis ermöglicht: die langsame Erarbeitung einer
Problemstellung. Es ist also zu unterscheiden zwischen
Bewegte Mathematik: wenn man
sie zu früh einsetzt, wirken sie teilweise allzu suggestiv
(verraten schon alles) - und sind dann vermeintlich in wenigen
Sekunden erledigt. Vor allem rauben sie den Schülern, was überhaupt
erst Erkenntnis ermöglicht: die langsame Erarbeitung einer
Problemstellung. Es ist also zu unterscheiden zwischen -
Modellen, an denen gewisse Erkenntnisse überhaupt erst erarbeitet werden - und die somit früh eingesetzt werden können,
-
Modellen, die Erkenntnisse zusammenfassen - und somit erst spät eingesetzt werden sollten.
-
-
Am interessantesten an der Herstellung der Modelle ist für mich, dass für fast jedes Modelle eine neue technische Idee gebraucht wird. Und überhaupt erst die technischen Umsetzungsmöglichkeiten bringen mich oft auf entscheidende didaktische Ideen. Ich setze also fast nie vorher fertig geplante Modelle um, sondern mein Modellbau ist meistens "work in progress", und vielen meiner Modelle sieht man die Spuren ihrer Erarbeitung noch an. Eigentlich müsste man jedes Modell, nachdem es mit allen Umarbeitungen fertig gebaut ist, nochmals ordentlich neu bauen.
Schön, wenn man solch visuelle Ästhetik für den Mathematikunterricht nutzen kann!)
- Im Idealfall würden auch die Schüler nicht nur von mir vorgefertigte Modelle handhaben, sondern selbst welche herstellen
(in sogenannten "Differenzierungskursen" in der Mittelstufe war sowas teilweise mal möglich; aber auch da haperte es an einer brauchbaren schuleigenen Werkstatt) .
-
Leider ist aber im zunehmend wie unter Margot Honecker reglementierten Unterricht, in dem zudem alle gebannt wie Kaninchen vor der Schlange der zentralen Prüfungen sitzen, kaum mehr Zeit für (wichtiges!) Basteln
(dabei wäre es gerade für Gymnasiasten wichtig,
- sich endlich mal im wortwörtlichen Sinne die Finger schmutzig zu machen,
- elementare handwerkliche Fähigkeiten zu erwerben
- Respekt vor handwerklichem Können zu bekommen) .
-
Standardzutaten: Tesa-Film, Textilklebeband in verschiedenen Farben,
 -Teile, Gummibänder, Hart-PVC-, MDF- und
Spanplatten, Holzleisten, Plexiglas, Laminierfolie,
-Teile, Gummibänder, Hart-PVC-, MDF- und
Spanplatten, Holzleisten, Plexiglas, Laminierfolie,  .
. -
Von besonderer Bedeutung ist bei meinen Modellen eine sinnvolle Farbgebung
Leider gibt es aber nur wenige auch aus großer Entfernung klar unterscheidbare Farben - und noch weniger passende Tafelkreide und Textilklebebänder.
-
Wo immer es möglich ist, beziehe ich die großen Entdecker und somit die Mathematikgeschichte ein, denn es ist dringend nötig, die "menschliche" Seite der Mathematik mitzuliefern, d.h. Freund und Leid des oftmals mühsamen Forschens, aber auch die grandiose Schönheit des menschengemachten mathematischen Gedankengebäudes:

-
Mein großes Vorbild sind die Technik-Erklärungen in
 , und fast möchte ich glauben:
, und fast möchte ich glauben:-
was man nicht Kindern erklären kann
(und die meisten Erwachsenen sind auch nicht schlauer) ,
hat man auch selbst nicht verstanden;
-
die grundlegenden Ideen einer jeden wissenschaftlichen Erkenntnis lassen sich
(mit altersgemäßen Beispielen)
auch Kindern erklären;
-
die Kindererklärungen sind auch für die Wissenschaftler selbst hilfreich
(sie müssen es nicht erst für Kinder vereinfachen, sondern das Geheimnis ihres Erfolgs liegt u.a. darin begründet, dass sie selbst noch so einfach denken, d.h. im Komplexen einfache und damit überhaupt erst verstehbare Strukturen entdecken können) .
-
-
Mir schwebt eine mathematische Version von

Christopher Polhems
(*1661 +1751)
![]() "mechanischem Alphabet" aus 80 Modellen
"mechanischem Alphabet" aus 80 Modellen

vor, mit dem er Schülern der von ihm gegründeten
Ingenieursschule "Laborium mechanicum" die wichtigsten mechanische
Bewegungsabläufe veranschaulicht hat:
also ein "mathematisches [Modell-]Alphabet", mit dem von A (5. Klasse)
bis Z (Abitur) der Schulstoff begreifbar wird, oder genauer: die
zentral wichtigen mathematischen "Ideen".
Modelle
3D-Modelle
Zahlensysteme als drehbare "Uhren" und Lineale

![]()
(Lineal, 122 = 144 cm
lang)

![]()
(Lineal, 102 = 100 cm lang)
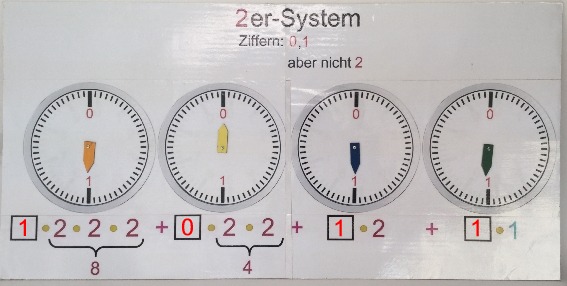

(Lineal, 28 = 256 cm lang)

Geodreieck mit beweglichem gelbem Winkelzeiger

(auch zum Spiegeln umbaubar)

aufspannbarer 360 0 -Winkelmesser


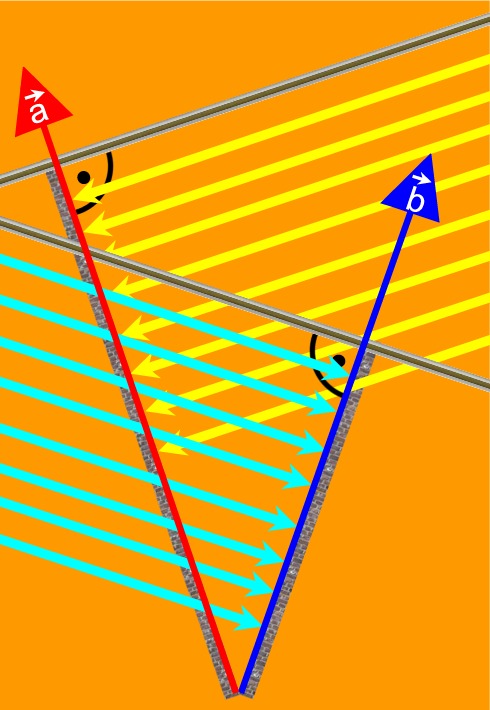
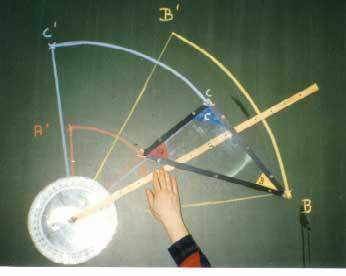
Thalessatz-Modell

 ..
..
wobei der konstruktionsbedingte Zeiger von M aus gleichzeitig auch die Beweisidee liefert

Scherungsmodell 1
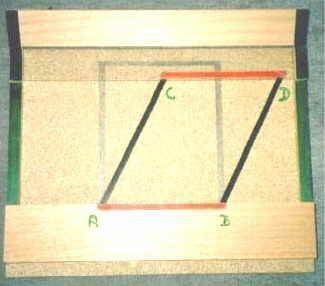


Scherungsmodell 2


("kleiner" Nachteil des Modells: um "Fenster" zu erreichen, die 30 x 20
cm groß und somit auch noch hinten in einem Klassenraum sichtbar sind,
muss das Modell aus mechanischen Gründen [siehe Rückseite] 200 x 60 cm
groß sein)

Drehungsmodell

"Kommamaschine"

mit nach vorne klappbaren weißen Tafeln, auf die Ziffern
(hier 2, 0, 7, 0 und 3) geschrieben werden können;
das Komma ist frei verschiebbar

Oberfläche, Volumen und 2D-Projektion eines Quaders


mit abnehmbaren Seitenflächen
Abwicklung: 
2D-Projektion

mit vorgehängter Folie

mit vorgehängtem Strahlen zum Fluchtpunkt


2D-Projektionen
 |
→ |
 |
 →
→


Pseudowürfel
von vorne: 
von oben: 

Cavallieri-Verfahren für verschiedene dreidimensionale (auch Misch-)Formen

(die Mittelachsen sind biegbar)






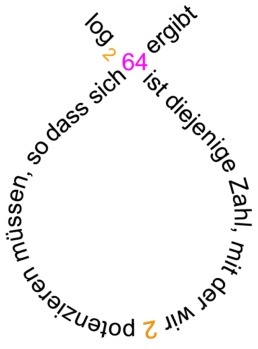
Prozent-Gummiband




In das weiße Feld oben lassen sich verschiedene Zahlen (hier 17)
eintragen;
eine ganz ähnliche Schlange wäre - nebenbei gesagt - für den Logarithmus
möglich:

Bruchrechnung an einer Pendeluhr

oder übersichtlicher angeordnet













und nun endlich die Bruchrechnung:


Abzählbarkeit der rationalen Zahlen
(durchaus auch schon in der Mittelstufe
"machbar",
denn warum sollten wir Schülern weiterhin die interessanteste
Mathematik vorenthalten?)






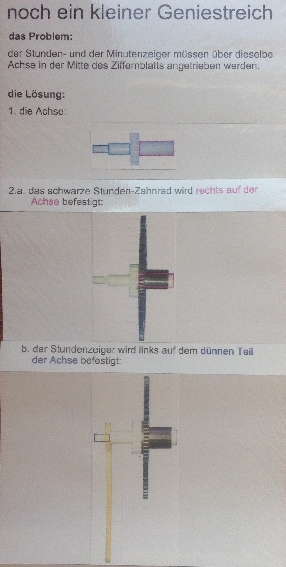
Kommutativgesetz-Maschine
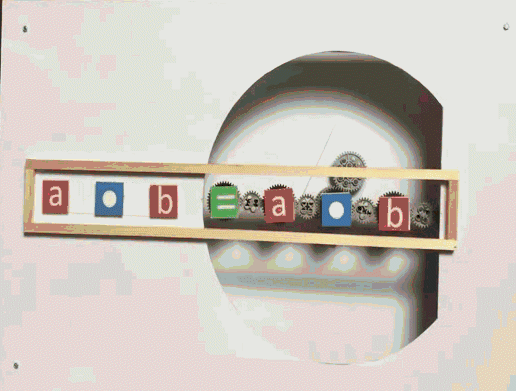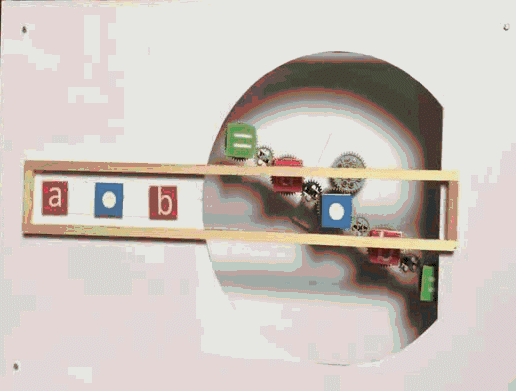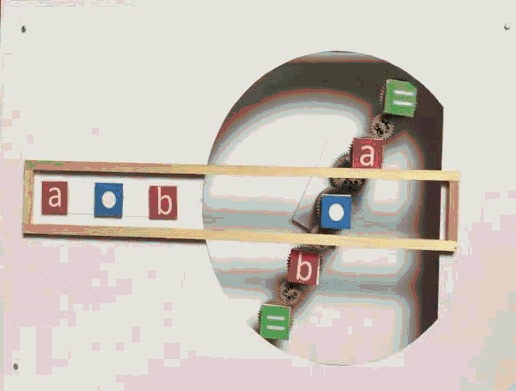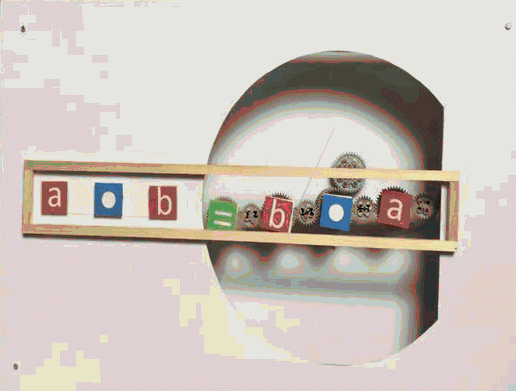
Dabei sind die Variablen a
und b durch
konkrete Zahlen ersetzbar,
und statt • können
auch + ,
- und
: eingesetzt werden:
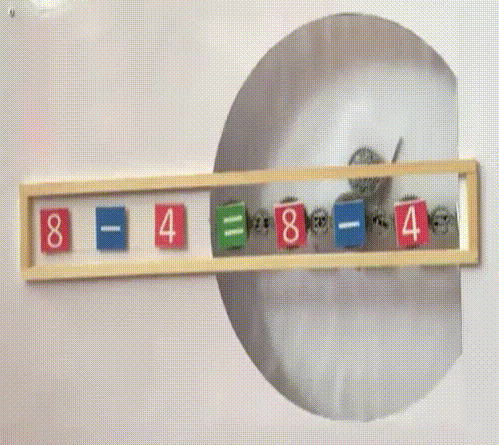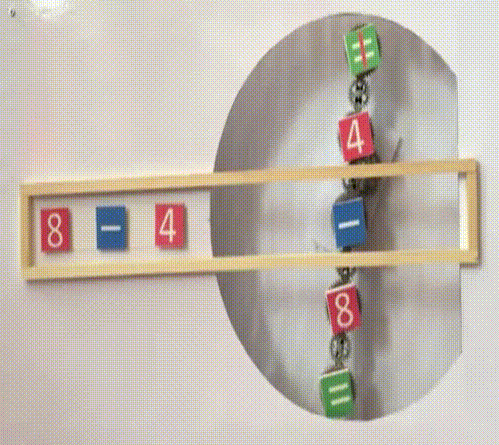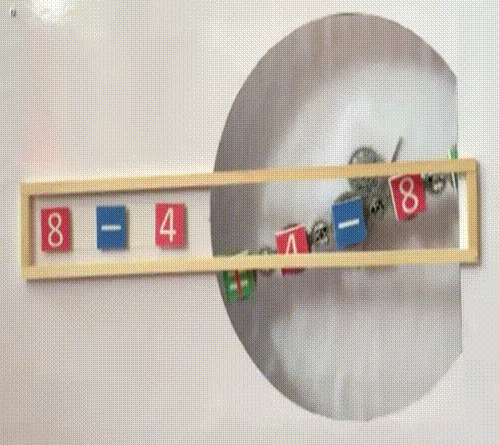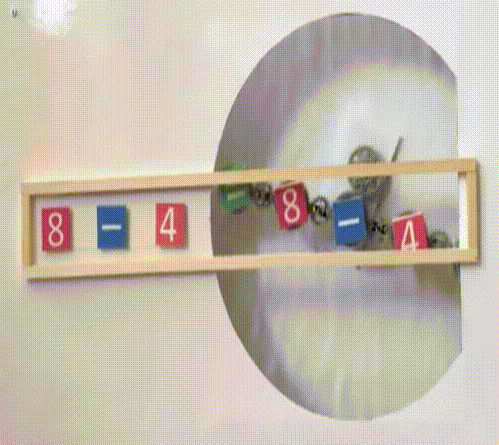

Termumformungskette

(ca. 2 m lang)
die Kette kann zusammengefaltet werden
 ,
,
so dass am Ende der schwierigste (Anfangs-)Term
und der einfachste (End-)Term
nebeneinander liegen:


Gleichungsjalousie



Beweis des Kathetensatzes

mechanische Version von 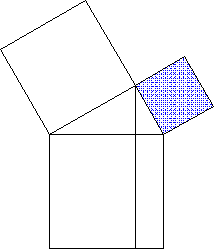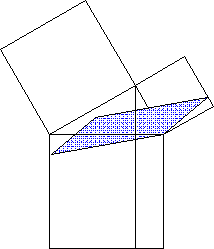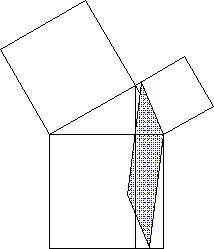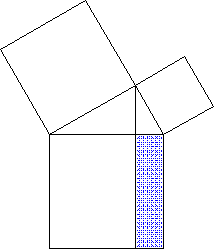

Beweis des Satzes des Pythagoras
Zu beweisen:

 +
+
 =
= 
Für diesen Beweis schmeißen wir
erstaunlicherweise
 und
und  sofort wieder weg
sofort wieder weg
und behalten nur  und
und  :
:

Nun legen wir  noch weitere drei Mal um
noch weitere drei Mal um
 herum,
herum,
indem wir sie an Scharnieren nach vorne klappen
(bisher waren die drei  hinter
hinter  verborgen):
verborgen):

So entsteht das neue, größere Quadrat 
(nur dann, wenn die  rechtwinklig sind!).
rechtwinklig sind!).
Die Fläche von  berechnen wir nun auf zwei
Arten:
berechnen wir nun auf zwei
Arten:
|
Aus 1. und 2. zusammen
folgt:  + 2 + 2  = =
 + +  Wenn wir nun auf beiden Seiten der Gleichung 2  wegnehmen, erhalten
wir
wegnehmen, erhalten
wir =
=  , ,und das ist ja eben der Satz des Pythagoras, den wir beweisen wollten (aus dem jetzt urplötzlich alle das ja eben ist der Witz am Satz des Pythagoras: er funktioniert nur an rechtwinkligen Dreiecken, handelt aber nur von Quadraten). |


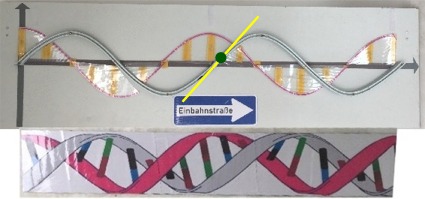
3D-Sinus-Spirale

Nachbau von
![]()

Vgl.

Western Sidney International Airport

Sinus-Zeichner

(veränderter und vereinfachter Nachbau von

Tangensmodell

und mit Kreistangente oben das Cotangensmodell

alte Auto-Scheinwerfer
vorne eine (komplizierte) Fresnel-Linse
 ,
,
dahinter ein einfacher Parabolspiegel
 .
.

(die Umwandlung der normalen Konvex- in die Fresnel-Linse
[und umgekehrt] erfolgt,
indem man das Modell auf den Kopf stellt)
neue Auto-Scheinwerfer
vorne simples Glas, dahinter ein (komplizierter)
Fresnel-Spiegel
 .
.


(mit dem gleichen Umdreh-"Mechanismus" wie bei der Fresnel-Linse)
(Nebenbei: der allerneueste
Schrei sind Matrix[!]laserscheinwerfer
aus 40 000 individuell
verstellbaren Minispiegeln,
also eine Art Micro-Fresnelspiegel.)

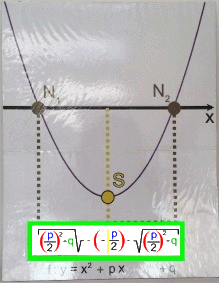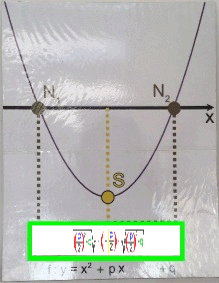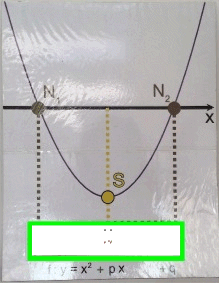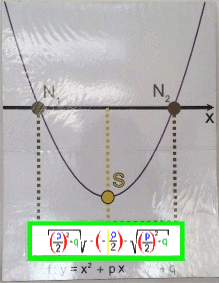
pq-Formel

Funktionenschieber

darin eingelegbare Hintergrundbilder:


Funktionsscharen
im Kreis angeordnet

[es geht mir da durchaus auch um den ästhetischen Reiz]
nebeneinander angeordnet


[das wird zwar oft als
Parabeln verkauft, sind aber in Wirklichkeit ziemlich
anspruchsvolle
![]() Kettenlinien,
Kettenlinien,
was aber nicht ausschließt, sie durch Parabeln
anzunähern
[die orangen Graphen sind annähernd
Normalparabeln,
die anderen gestreckt oder
gestaucht])

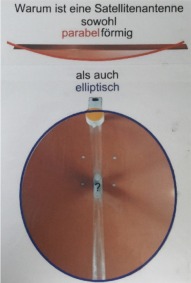
Parabolantenne



verstellbarer Proportionszirkel, mit dem man Gegenstände vergrößern kann

(zwecks Einübung / Anwendung der Strahlensätze)

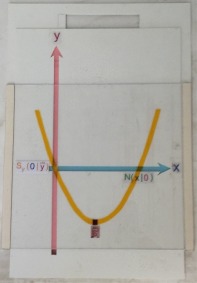
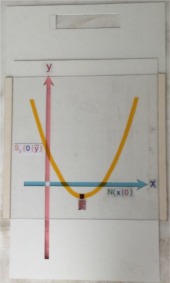
vertikal verschiebbare Parabel

"drehbare Sinus- und Cosinusmaschine"
00: 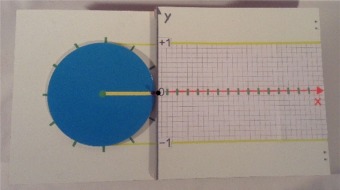
300: 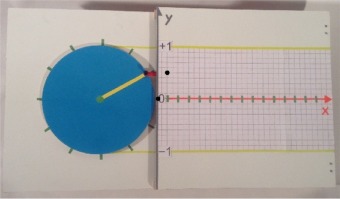
600: 
900: 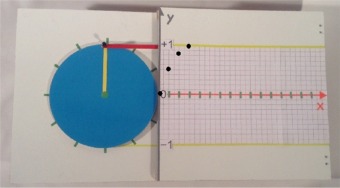
ganz wichtig: aufgeklappt erkennt man die "Gestänge-Mechanik"
00: 
300: 
600: 
900: 
Und hochkant ergibt sich der Cosinus


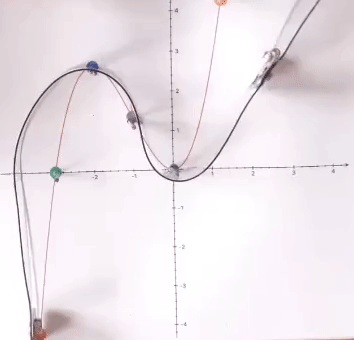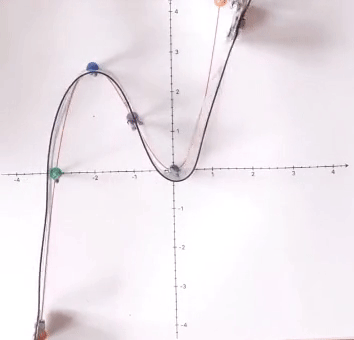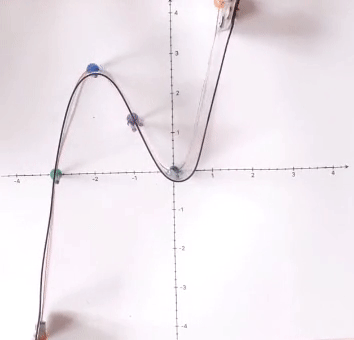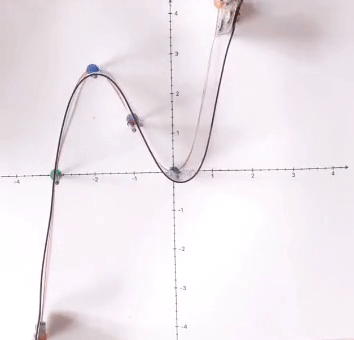
er- fahrbare Funktionsgraphen
(der Punkt P
samt der Tangente in ihm
ist beliebig auf der Graphenschiene verschiebbar)



(das Pferd wird erst am Ende in den
Sattel[!]punkt gelegt)
(hier sind in gelb schon die jeweiligen Steigungen
eingelegt;
die Kurve ist für frühe "Kurvendiskussionen" auch schon dann
geeignet,
wenn der Sinus noch gar nicht durchgenommen wurde)
in die Graphenschienen einhängbarer Mechanismus zum Ablesen von Rechts- und Linkskurven:


Kunststoffstreifen-Funktionsgraphen


"Exponentialmaschine"

Das oberste Zahnrad dreht sich durch
einen Elektromotor ein Mal pro Sekunde.
Jedes Zahnrad dreht sich fünf Mal so schnell wie das nächttiefere.
Dann dreht sich das unterste Zahnrad ein Mal in 25000
Jahren
- und kann deshalb getrost erstmal einbetoniert werden.

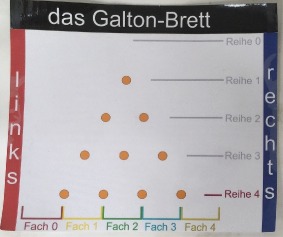
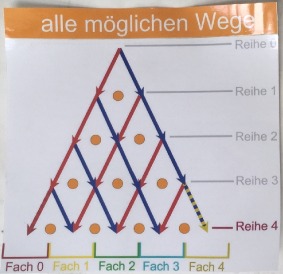
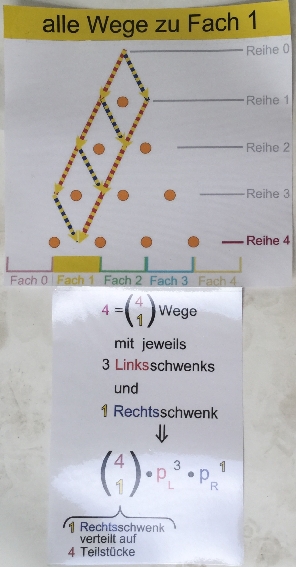
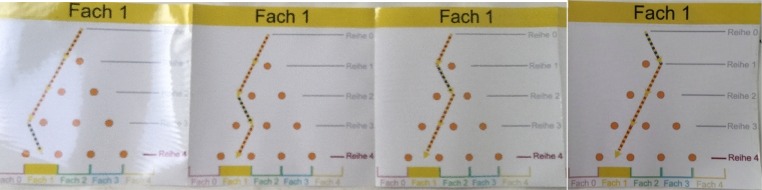
Galton-Brett

Viel interessanter ist allerdings:


verschiebbare Binomialkoeffizienten und Exponenten






Sicherheit und Wahrscheinlichkeit
p = 0: 
p = 0,2: 
p = 0,5: 
p = 1: 
(hier nicht zeigbar ist der Mechanismus,
mit dem der goldene Punkt bei p = 0 und p = 1 automatisch einrastet,
so dass die Sicherheit spürbar von der "fließenden"
Wahrscheinlichkeit unterschieden wird)

Gauß- bzw. Glockenkurve


(hier nicht montiert ist ein Mechanismus,
mit dem man verschiedene Standardabweichungen einstellen kann)

kollineare Vektoren

(die oberen Platte ist mit der roten Kurbel links
unten drehbar,
so dass alle Vektoren auf ihr gemeinsam in verschiedene Richtungen
schwenken)

(nicht) kollineare Vektoren




(nicht) komplanare Vektoren
von oben

die von den Vektoren ![]() und
und ![]() augespannte Ebene E
augespannte Ebene E
(hier liegt ![]() noch in E)
noch in E)
von vorne

(auch hier liegt ![]() noch in E)
noch in E)




(nicht-)kollineare und (nicht-)komplanare Vektoren


vektorielle Gerade

(alle Vektoren sind aus Gummibändern und dadurch frei
beweglich;
hier nicht montiert ist ein Normalenvektor)

vektorielle Gerade und Ebene (weiß)




Abstand windschiefer Geraden


geschlossene Vektorzüge



Projektionsvektoren fürs Skalarprodukt
leer

Folie von rechts davor geklappt, Projektion von ![]() auf
auf ![]()
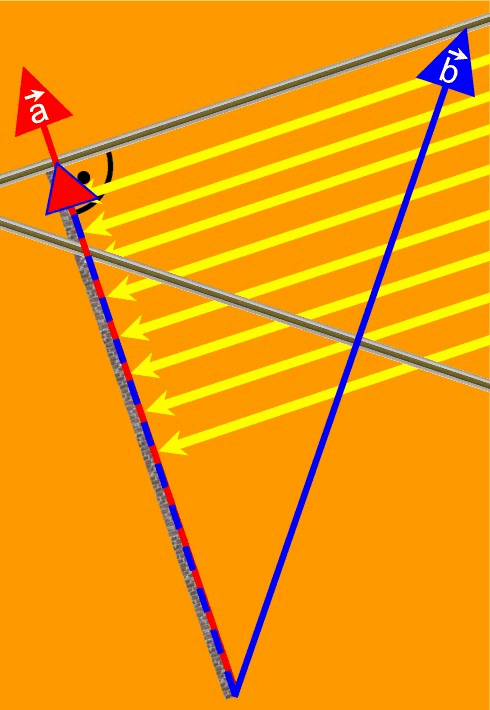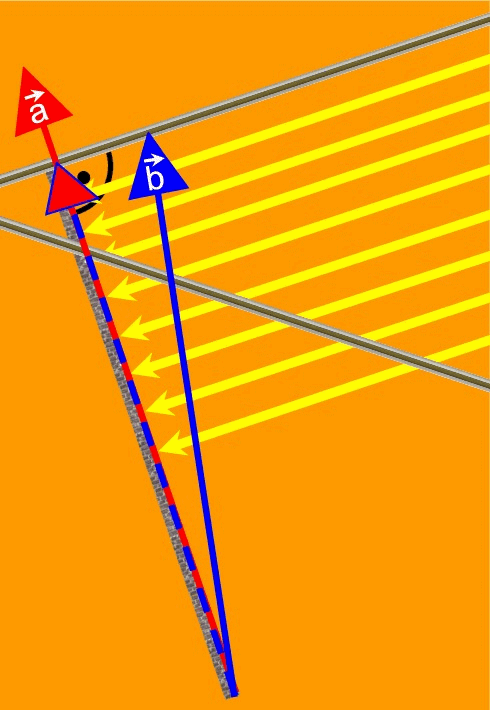
Folie von links vorgeklappt,
Projektion von ![]() auf
auf ![]() :
:
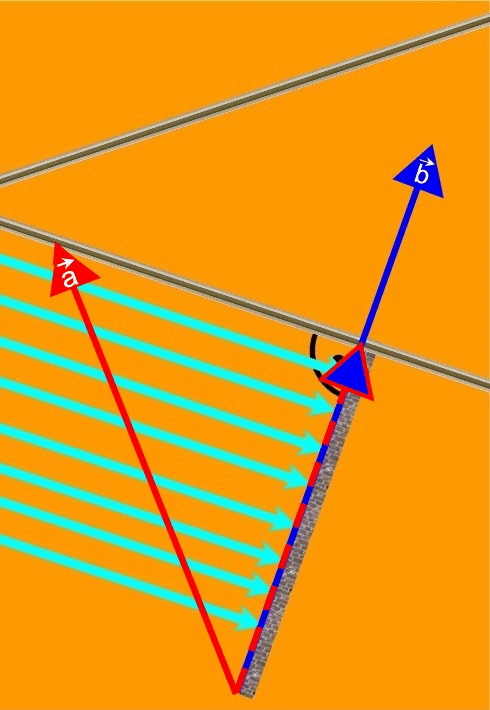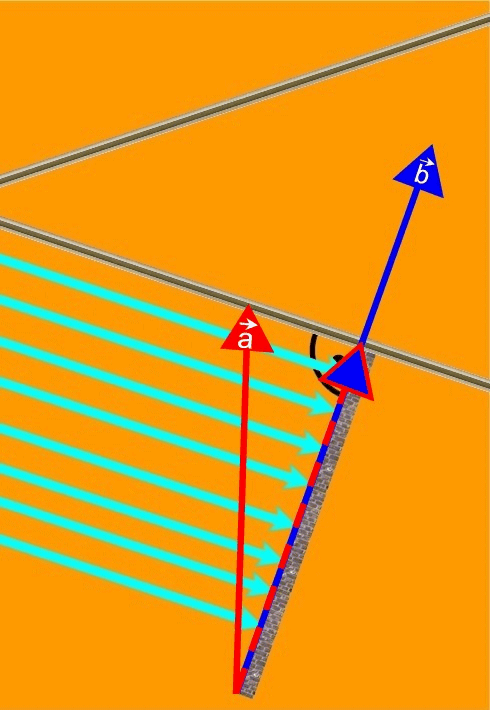
beide Folien vorgeklappt:


vektorielle Ebene und Normalen(einheits)vektor



Schnittgerade zweier Ebenen

mit Richtungsvektoren der beiden Ebenen:

Ebenenrichtungsvektoren an Anfang des Geradenrichtungsvektors verschoben:

Geradennormalenvektoren in den beiden Ebenen
(Winkel zwischen diesen beiden Vektoren = Winkel zwischen
den beiden Ebenen;
das muss man ja nicht alles ausrechnen, aber man sollte es
anschaulich verstehen):

einfachere Methode der Winkelberechnung:

(Winkel den Ebenen = [Ergänzungs-]Winkel zwischen den
beiden Ebenennormalenvektoren)

Satz von Varignon
(die Verbindungsstrecken der Seitenmittelpunkte des
gelben Vierecks bilden immer ein Parallelogramm,
was überhaupt erst wirklich erstaunlich wird, wenn man das Viereck
kontinuierlich "verbiegt";
der Satz ist vektoriell wunderbar einfach beweisbar)
2D-Version
mit an den Ecken
aufeinanderliegenden Leisten:
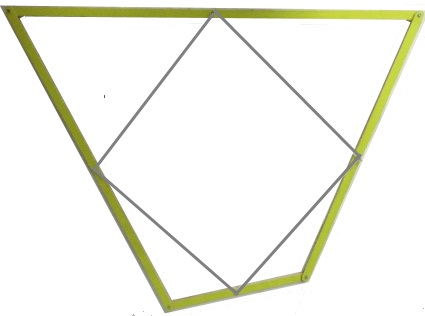

3D-Version
mit Gummizug in den
blauen Röhrchen:



vektorieller Kreis
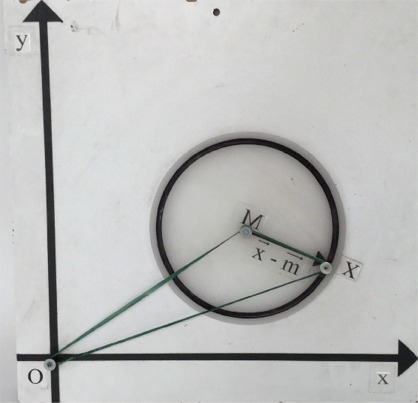
(um den Mittelpunkt M drehbar)




Ellipsograph 2




Apollonischer Kegel 1
(benannt nach Apollonios
von Perge
[* ca. 265 v. Chr. in Perge (südliches Kleinasien, heute
Türkei); † ca. 190 v. Chr. in Alexandria])
basierend auf einem 80 cm hohen, käuflich zu
erwerbenden Styroporkegel



 |
 |
 |
 |
||
| Kreis | Ellipse | Parabel | Hyperbel |
(Ich höre schon den Einwand, Hyperbeln kämen im üblichen Unterricht doch kaum und Ellipsen gar nicht vor.
Genau das finde ich aber
wegen der Schönheit/Eindrücklichkeit wie auch mathematikhistorischen Bedeutsamkeit des Apollonischen Kegels
irgendwo zwischen schade und unverzeihlich.)

Apollonischer Kegel 2


(Das war mir auch neu:
alle Kegelschnitte parallel zu einer Seitenschräge
sind Normalparabeln, wenn auch in verschiedenen Maßstäben.)

Hyperboloid




 zusammengefaltet: langweilig |
 auseinandergefaltet: ästhetisch reizvoll |
||
 Hyperboloid-Ausschnitt |
|||




Goldener- Schnitt- Zirkel
(stilecht mit goldenem mittlerem Zeiger)


Oloid




Möbius-Band


Frage:
ist es möglich, einen Würfel samt innen ausgekleidetem "Tunnel"
origamimäßig aus einem einzigen Stück zu bauen?
Antwort:





Wenn man schon im Matheunterricht (!)
Brunelleschis Kuppel des Doms in Florenz
und seine Entdeckung der Zentralperspektive anhand des

Baptisteriums
durchnimmt,
dann aber auch an einem eindrücklichen Modell:

(1,3 m hoch)
kleiner zusätzlicher eyecatcher:

Regenschirm in Form von Brunelleschis Kuppel

platonische Körper
und



(stl-Datei für den 3D-Druck:
![]() )
)

zur Mathematik der Cheops-Pyramide



(hier nicht gezeigt: die Poster zur Mathematik des
Eiffelturms
und zu den 72 Namen [u.a. von Mathematikern] rund um die untere
Plattform)


 |
"Oft fügt es
sich, dass sich bey den gewöhnlichen Beschäftigungen und
Handthierungen des Lebens Gelegenheiten darbieten,
mehrere merkwürdige Operationen der Natur zu beobachten;
ja sehr oft könnten die interessantesten physikalischen
Versuche beynahe ohne irgendeine Mühe oder Ausgabe
mittels der Maschinerien angestellt werden, die man bloß
zu den mechanischen Zwecken der Künste und Manufakturen
vorgerichtet hat." |
|
 (Paul Stein-hardt) |
"Zu den
selbstvergessenen Spielern gehört auch Paul Steinhardt,
ein Physiker an der University of Pennsylvania, der sehr
wohl weiß, wie wichtig das spielerische Element in der
Forschung ist. Steinhardts Büro ist vollgestopft mit
Spielsachen. Zwischen Büchern und Computern, den
Versatzstücken ernsthafter Wissenschaft, finden sich die
verschiedensten Modelle - von behelfsmäßigen
Pappkonstruktionen, die durch Klebeband zusammengehalten
werden, bis hin zu kostspieliger Computergraphik. Da
gibt es nichts, was Steinhardt nicht für seine Zwecke
hätte brauchen können: Kleiderbügel, Schaumgummibälle,
Spielwürfel, Acetatplatten, Lego®steine, Zahnstocher,
Zeichenkarton." |
Wer Mathemodelle baut, tut gut daran, direkt neben einem gutsortierten Baumarkt zu wohnen, der die meisten der für die Modelle benötigten Materialien vorhält. Was es nicht in Baumärkten gibt, liefern dann spezielle Bastelläden.
In Baumärkten gibt es aber nicht nur Materialien für Modelle, sondern vor allem in den 1€-Grabbelkisten im Kassenbereich auch allerlei Schnickschnack, der zweckentfremdet direkt als Mathemodell dienen kann
(und sonstige Läden liefern den Rest).
Z.B.:
"Integrator"

(eigentlich zum passgenauen Verlegen von Parkett um
Ecken gedacht)

"3D-Integrator"
1

Rasterschaumstoff,
wie er z.B. in Werkzeug-, Kamera- und Musterkoffern vorkommt,
aber auch einzeln erhältlich
ist:


Gleichung = Waage


Kongruenzabbildungen
man verschiebt ein erstbestes Buch, schwenkt (dreht) es und dreht (spiegelt) es auf den Rücken;
Überprüfung der Kongruenz zweier Bücher:
man legt eins vor das andere und umgekehrt
(d.h. man zeigt alltägliche Kongruenz, statt sie völlig zu abstrahieren und unnötig zu verkomplizieren)

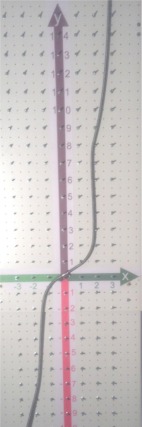
Rohrreinigungsspirale als Universalfunktionsgraph


|
Eine solche biegsame
Spirale ist eine "handschmeichlerische" Manifestation sowohl
der Stetigkeit als auch der
Differenzierbarkeit (wer sie mit Gewalt knickt, macht
sie kaputt). |

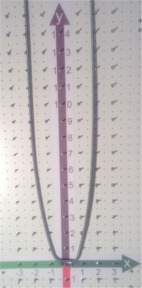
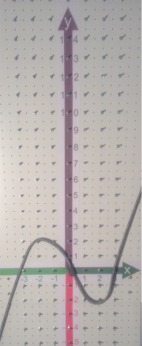

"Wickelband" als Universalfunktionsgraph:
- 86 cm lang,
- universal biegbar,
- in
der jeweiligen Form verbleibend)

Bei der Einführung des Wahrscheinlichkeitsbegriffs sind
alle industriell gefertigten Würfel

völlig witzlos, da sie augrund der Präzision ihrer Herstellung
allesamt laplace-, also gleichmäßig verteilt sind
(worauf sich die Käufer ja auch verlassen).
Viel erhellender sind unregelmäßige "Würfel"
wie z.B.

(da liegt doch immerhin die Vermutung nahe,
dass die Wahrscheinlichkeiten der Seiten sich verhalten wie deren
Größen).

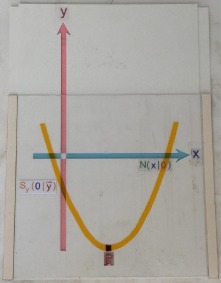
"y = ax2 -Männchen"


"Rotationskörper-Hersteller"

(eigentlich ein Milchaufschäumer)

"Normalenvektor"


"stumpfe-Winkel-Messgerät"





"Radiuszirkel"






"Parallelometer"


vektorielle Gerade

vektorielle Ebene


kollineare Vektoren


Cavallieri-Verfahren


Cavallieri- und Integrationsverfahren für Rotationskörper


Bestimmung der Kugeloberfläche und des Kugelvolumens


2- und 3D-Strahlensatz-Rankgitter



Schachtelset für Kreisumfang und -fläche


Tortenring für den Kreisumfang

(solch ein Tortenring wird beispielsweise benötigt,
um eine
Cremeschicht schön gerade auf einen Tortenboden zu bekommen;
größter
Vorteil des Tortenrings ist, dass er kontinuierlich verstellt
werden kann)

(Einstellung beim Kreisdurchmesser 16 cm;
aus konstruktiven Gründe
muss das Maßband leider innen befestigt sein)

(Einstellung beim Kreisdurchmesser 32 cm)
dazu zusätzlich eine Kreisscheibe mit den eingefrästen ganzzahligen Radien 8 cm, 9 cm, 10 cm ... 15 cm:

(grün markiert ist dabei der Kreis mit dem Radius 10 cm = 1 dm, also der
Einheitskreis;
das innere Maßband des Tortenrings hat auch die
Maßeinheit dm)


ein Muqarnas-Modell




Sierpinski-Dreieck als Popup


quadratische und dreieckige Sierpinski-Pyramide






Vierungen
(mit farbigen Ellipsensegmenten):
romanisch:
 |
 |
||
| von oben / vorne mit Rosettenfenster |
von oben / der Seite |
||
 |
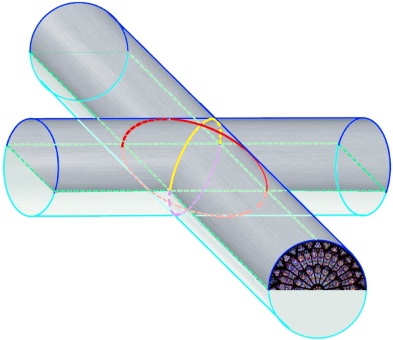 |
||
| von unten |
gotisch:
 |
 |
||
| von oben / vorne mit Maßwerk |
von oben / der Seite |
||
 |
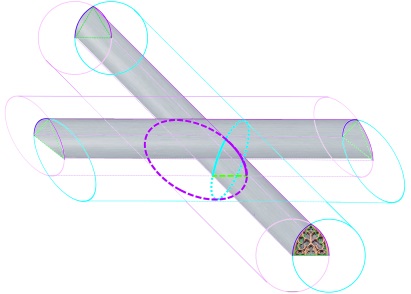 |
||
| von unten |

Doppelpendel / Dreikörperproblem
(also endlich mal etwas relativ Einfaches, was nicht berechenbar ist - und sich anschaulich chaotisch verhält)

... mit Lampe und fluoreszierender Kreisfläche, vgl.
Nicht detailliert gezeigt werden hier zig kleine "Fertigmodelle", die
-
teilweise mathematische Sachverhalte veranschaulichen,
-
teilweise nur Spaß an geometrischen Formen vermitteln sollen:

(kleine Auswahl; es fehlen z.B. alle Poster zu wirklich aktueller Mathematik)
-
Leider habe ich einige Poster gerollt aufbewahrt - was man ihnen auch ansieht.
-
Poster sind im Vergleich mit beweglichen Modellen natürlich immer nur die zweitbeste Lösung.
-
Damit die Poster von allen Schülern im Klassenraum gesehen werden können, sind sie sehr groß. Die folgenden kleinen Abbildungen können daher nur einen ersten Eindruck liefern - und teilweise ist auf ihnen die Schrift so klein, dass man sie kaum lesen kann.
-
Viele Poster enthalten Merksätze - und hängen daher manchmal für lange Zeit in den Klassenräumen
(teilweise auch während Klassenarbeiten).
-
Am liebsten hätte ich einen eigenen Klassenraum, der liebevoll mit Mathebüchern, Postern und Modellen vollgestopft wäre.
-
Ich erlaube mir auf den Postern manchmal eine mathematisch "unsaubere", aber für Schüler verständliche und anschauliche Sprache:
"Ich hatte das Glück, auf Bücher zu treffen,
die es nicht allzu genau nahmen mit der logischen Strenge [...]"
(Albert Einstein)
Symmetrie:
a) keine Symmetrie:

b) achsensymmetrisch zu einer Achse:

c) achsensymmetrisch zu zwei
zueinander senkrechten Achsen,
also auch punktsymmetrisch:

d) achsensymmetrisch zu mehreren nicht zueinander senkrechten Achsen:

e) Ellipsen:
f) schiebesymmetrisch (als nun doch wieder bewegliches Modell):


g) drehsymmetrisch (auch wieder als bewegliches Modell):

h) motorbetriebene Achsensymmetrie:


(unten unser Schulgebäude,
wobei eine Drehung um die rot
markierte
und Drehungen um die blau
markierten Achsen möglich sind)
i) optische Täuschung:
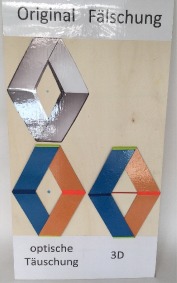

j) Muster erkennen bzw. konstruieren:























  |
   |

Ihre volle strukturell-ästhetische Wirkung
entfalten die folgenden Poster erst,
wenn Schüler sie selbst sortieren
(und zwar wegen der Größe der Poster auf dem
Fußboden der Pausenhalle)

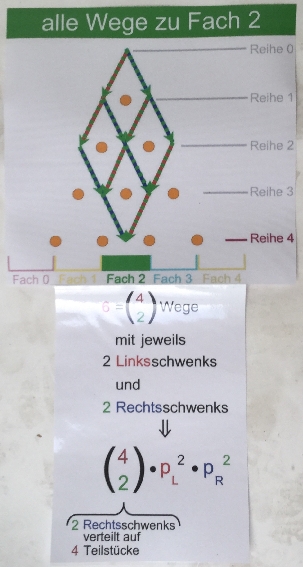
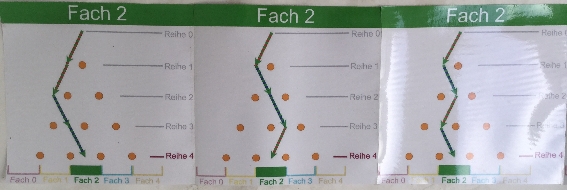
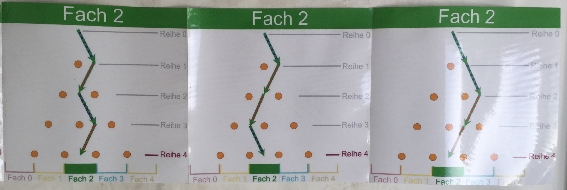
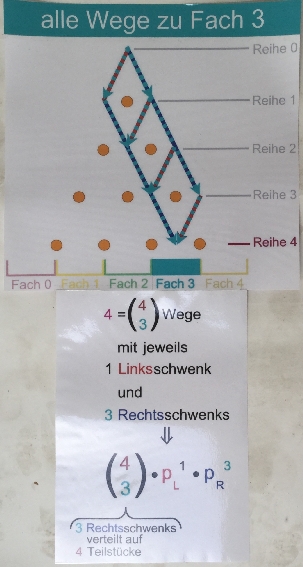
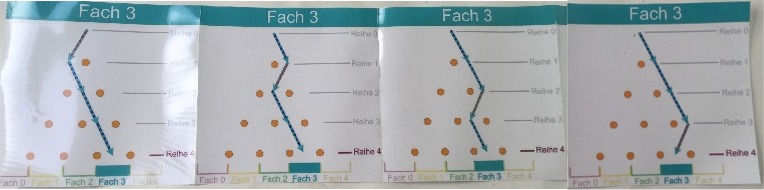
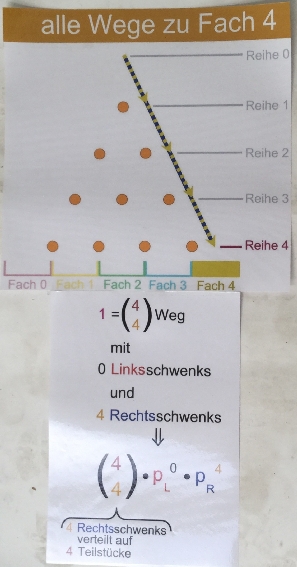

die Null in der (Schul-)Mathematik

ein Mal aufgeklappt:

links und rechts Cover von Büchern zum Thema
"Null";
in der Mitte links die Geschichte der Null,
rechts eine Erklärung, warum man nicht durch Null dividieren
kann
zwei Mal aufgeklappt:
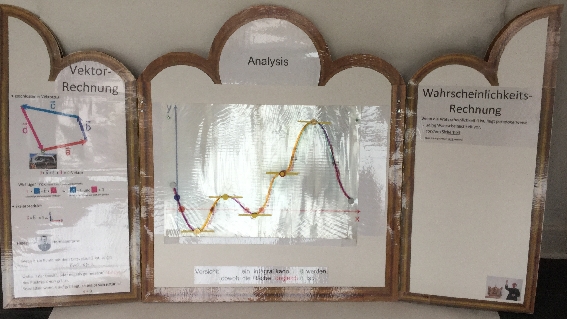
der Grund für die Triptychon-Form:
die drei Teilgebiete der Schulmathematik - und die Rolle der
Null in ihnen

1,5- m- Rosette auf dem Boden vor dem Lehrerpult
(Winkel werden hier gegangen)


zwecks Bruchrechnung und als Ergänzung zum Musikunterricht:
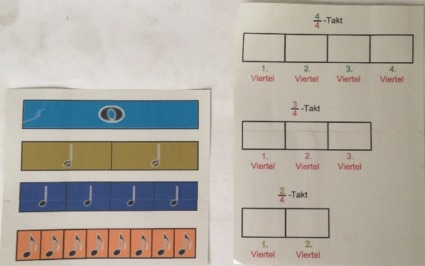
(die bunten Noten gibt es dabei auch als kleine
Zettel, um sie in die Takte legen zu können)

Oder warum dürfen Schüler denn nichts
(auf Postern im Mathematikunterricht!)
über diese Bilder



und ihre vielfältigen, u.a. mathematischen
![]() Hintergründe erfahren?:
Hintergründe erfahren?:















 )
)

 ,
,