| mein persönliches Stalingrad | oder | das Herz der Ableitung |
Carmina Burana
(Texte aus dem 12. Jahrhundert, vertont von Carl Orff)
| O Fortuna | O Fortuna, |
Ab und zu eine kleine stalinistische Selbstbezichtigung ist ja auch ganz nett
(ach ja, ich weiß, über Stalingrad und die Moskauer Schauprozesse macht man "eigentlich" keine Witze, und die benutzt man auch nicht unnötigerweise als Metaphern):
| man bleibt aufmerksam und wird wieder im besten Sinne demütig. |
Genau solche (durchaus selbstbewussten!) Selbstbezichtigungen (vgl. auch ![]() "Mit Methode scheitern") kommen mir in der pädagogischen Diskussion viel zu selten vor, bzw. diskutiert und laut reflektiert wird ja fast nie, sondern es werden immer nur Patentrezepte ausgegeben oder Meinungen aufeinander gehetzt.
"Mit Methode scheitern") kommen mir in der pädagogischen Diskussion viel zu selten vor, bzw. diskutiert und laut reflektiert wird ja fast nie, sondern es werden immer nur Patentrezepte ausgegeben oder Meinungen aufeinander gehetzt.
Dadurch hat auf die Dauer jedeR LehrerIn das Gefühl:
"bei allen anderen läuft´s dufte - nur bei mir nicht"
(was das Schweigen und den Trend zu "noli me tangere = schau´ bitte nicht in meinen Unterricht" nur verschärft)
| Es ist wohl im Lehrer- wie in jedem Beruf unvermeidbar, ja zwecks Verbesserung des eigenen Verhaltens sogar nötig, eine Achterbahnfahrt der Gefühle zu absolvieren. |
Ach, da war ich vor wenigen Wochen noch so herzerhebend gefeiert worden (vgl. ![]() ) - und dann das:
) - und dann das:
(welch geniale Neuheit :-)
unterrichtet, es schien auch alles "gut gelaufen" zu sein - und dann wiederholte ich es einige Wochen später mit den SchülerInnen.
Dann aber scheiterte alles an einer (scheinbar) nichtigen Stelle, nämlich in der ![]() "Zutatenliste" bei
"Zutatenliste" bei
3. die Ableitung von f, also f '
Oder genauer gesagt: als die Steigung m der Tangente in P ( x0 | ) gesucht wurde, kam keineR der SchülerInnen auf
m = f ' (x0)
| Typischer erster Effekt bei einem Lehrer: Erst war ich
|
| Das konnte doch unmöglich wahr sein, dass die SchülerInnen sowas ebenso Simples wie Zentrales nicht kapiert hatten!!! |
Erst dann dämmerte es mir so langsam:
| Typischer (?) zweiter Effekt bei einem Lehrer: wenn in einer durchschnittlichen Klasse keinE SchülerIn etwas Zentrales verstanden hat, so
|
Mich interessiert hier vor allem b., also
"die scheinbar so einfache Sache ist in Wirklichkeit gar nicht so einfach".
(und ein verändertes Verhalten des Lehrers, also a., hätte aus Überlegungen dazu zu folgen)
Was ist scheinbar so einfach?
(bzw. für einen Lehrer allzu selbstverständlich):
| Die Steigung eines Graphen im Punkt P ( x0 | ) ist f ' (x0), und das wurde hergeleitet aus (definiert als; s.u.): Die Steigung eines Graphen im Punkt P ( x0 | ) ist gleich der Steigung m der Tangente t in diesem Punkt. Also ist umgekehrt die Steigung m der Tangente t im Punkt P ( x0 | ) gleich f ' (x0): m = f ' (x0) |
Nun will ich nicht beim Klagen stehen bleiben.
(Auch das wird in pädagogischen Diskussionen oftmals nicht gesehen: dass die Reflexion von Misslungenem durchaus konstruktiv gewendet werden kann; wie überhaupt Reflexion leider oftmals im Rufe der Wehrkraftzersetzung steht, also als negativ empfunden wird.)
Sondern es wäre doch zu fragen:
warum ist das Kind da so mörderisch in den Brunnen gefallen
und wie kann man es wieder rausholen?
Wenn die SchülerInnen m = f ' (x0) nicht begriffen haben, so ist nicht deutlich genug geworden:
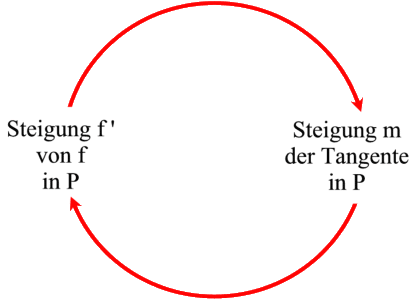
Das Problem - so scheint mir im Nachhinein - ist ein Doppeltes:
hatte ich die Umkehrung allzu leichtfertig vorausgesetzt
(da hätten die roten Pfeile vorher mehrfach durchlaufen werden müssen),
aber ist das Problem noch viel grundsätzlicher: es geht
ans Herz
der Ableitung,
des Definierens
und damit im Grunde der gesamten Mathematik,
aber auch ans Herz
der pädagogischen Vermittlung:
Für einen Mathematik(lehr)er ist das ja alles ganz (allzu!) einfach:
| die Tangente
|
Und genau da fangen die pädagogischen Probleme an:
Einerseits müssen die SchülerInnen irgendwann
(wann genau? - von Anfang an oder doch besser später?)
diesen mathematischen Denkprozess verstehen
(und zwar aus zwei Gründen:
, damit sie anhand der wahrhaft zentralen Ableitung verstehen, was Mathematik überhaupt ist, d.h. was typische mathematische Denkweisen sind;
, damit sie Aufgaben nicht nur unverstanden "runterrechnen" - und selbst das misslingt ja ohne Grundverständnis);
Andererseits: "wie sag´ ich´s meinem Kinde" bzw. "das sagt sich so leicht", dass es die doch offensichtliche Tangente gar nicht a priori gibt bzw. dass sie überhaupt als Limes der Sekanten "definiert" ist?
Für durchschnittliche SchülerInnen ist sowas schlichtweg gehirnausrenkend, ja, hier zeigt sich geradezu eine grundsätzliche mathematische Provokation, über die vielleicht wir sekundären LehrerInnen nicht mehr staunen können, die aber sehr wohl ganz große Geister
(allemal in früheren Zeiten, teilweise aber auch noch heute)
irritiert hat.
Zudem frage ich mich, ob nicht die unmathematische Anschauung von "Otto Normalverbraucher" ausreicht:
selbstverständlich gibt es die Tangente,
nur lässt sie sich schlecht (wackelig) zeichnen - und ohne Ableitung schon gar nicht berechnen.
Eine ganz andere Frage ist es allerdings, ob
für "Otto Normalverbraucher" nicht auch eine "nach Augenmaß" gezeichnete Tangente hinreichend genau ist,
geschweige dass er eine Notwendigkeit (?) einsieht, überhaupt Tangenten zu zeichnen bzw. zu berechnen.
Mit 1. und 2. zeigt sich ein grundsätzliches pädagogisch-didaktisches Problem, ja eine regelrechte Schizophrenie, die ich allzu leichtfertig angegangen hatte.
Das Problem ist oft genug in der fachdidaktischen Literatur bedacht worden, aber ich hatte es zu leicht genommen - oder es gibt bislang keine gelungene (eindeutige) Lösung?
Es gibt aber noch andere denkbare Gründe, weshalb die SchülerInnen
m = f ' (x0) nicht "sahen" (!)
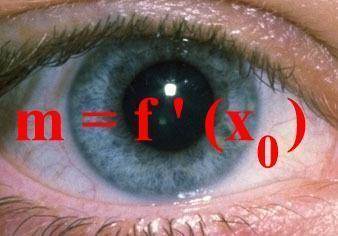 ,
,
also eine Tatsache, die uns LehrerInneN doch sofort "ins Auge springt"
(deretwegen die Aufgabe in
doch überhaupt nur gestellt wurde):
hat ein neues Problem für SchülerInnen oftmals rein gar nichts mit dem alten zu tun
(sie denken also merkwürdigerweise [???] nicht: das neue Problem wird doch garantiert nur gestellt, um das alte anzuwenden)
Hier steckt natürlich - das sei nur angedeutet - eine Herausforderung für den Lehrer: wie kann er dennoch auf "das Alte im Neuen" aufmerksam machen, ohne es zu "verraten"?
ergab sich im Laufe des Unterrichtsgesprächs, dass die SchülerInnen "immer noch nicht" ein anderes, noch
erheblich wichtigeres
und scheinbar einfacheres
Problem verstanden hatten, nämlich
oder genauer: wie Funktionen
(x → f(x)) darin eingezeichnet werden bzw. auftauchen.
Und im Folgenden sei gleich auch f ' (x) eingezeichnet
(genau genommen die Tangente mit der Steigung m = f ' (x) ):