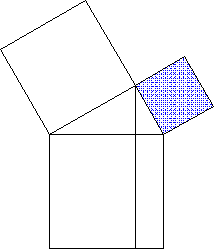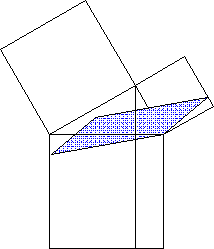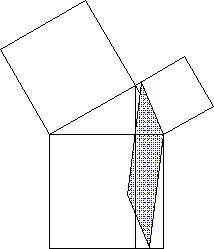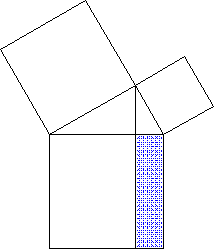MathematikbewegteMathematik
|
| "Die Software [...] kann sich an kommerziellen Programmen durchaus messen." |
 | Top-Link des Monats 11.2001 |
 | "Spitzenprogramme unter einer gemeinsamen Oberfläche!" |
| "Veranschaulichung nahezu aller fundamentalen Elemente der Schulmathematik" | |
| "[...] meine Gratulation zu Ihren tollen Anwendungen der bewegten Mathematik, die ich schon oft im Unterricht verwendet habe!" (T.R.) | |
| "[...] seit Jahren nun setzte ich Ihre B(ewegte)M(athematik) immer wieder im Unterricht ein und freue mich oft, wie einfach es sein kann, manche Sachverhalte quasi dynamisch zu verdeutlichen. Auch meine Referendare weise ich auf Ihr Werk hin und weiß, dass diese Ihre Arbeit ebenso schätzen. Ein Kompliment und Dankeschön für ihre vorzügliche Arbeit!" (V.M.) |
für die Visual-Basic-5.0-Programme (32 bit);
eventuell die entsprechenden dll´s laden
Diese Programme werden voraussichtlich nicht weiter verbessert und ergänzt. Ich bitte, eventuell enthaltene Fehler zu entschuldigen.
| "Bewegte Mathematik" steht für Programme nach einem einheitlichen Grundprinzip: was im Schulunterricht an der Tafel oftmals nur im Anfangs- und Endzustand zeigbar ist, wird durch die Programme als kontinuierliche Bewegung dargestellt. |
| Zur benötigten Software, der Bildschirmauflösung, der Installation und den benutzten Schriften siehe die Tips unten. |
| Die Programme sind FREIWILLIGE "Spendensoftware": für den Fall, daß sie Ihnen gefallen und Sie sie öfters benutzen, werden Sie um eine Unterstützung des
gebeten. |
Die Programme dienen der Veranschaulichung von bereits vorher Erarbeitetem, d.h. sie scheinen mir NICHT geeignet
Wenn meine Programme zu früh eingesetzt werden, verbergen sie (auch programmtechnisch) den Entdeckungsprozess hinter dem Ergebnis und würgen sie selbstentdeckendes Lernen vorzeitig durch allzu große Suggestivität ab.
Diese Suggestivität - zu früh eingesetzt - führt dazu, dass man nur noch staunt, es aber nichts mehr zu "sagen" und problematisieren geschweige denn zu finden gibt: die Mathematik fällt (mal wieder) nur wie ein Monolith vom Himmel:
Über die Mitteilung weiter gehender pädagogischer Erfahrungen mit meinen Programmen würde ich mich sehr freuen!
Die Programme umfassen weite Teile des Schulunterrichts:
| Geometrie: |
| Algebra: |
| Vektorgeometrie: |
| Analysis: |
| Wahrscheinlichkeitsrechnung/Statistik: |
Alle Programme sind in Visual Basic 5.0 (32 bit) erstellt und benötigen daher einige zusätzliche "Bibliotheken" (dll´s), die in der Datei msvbvm50.exe zusammengefaßt sind. Falls die dll´s auf Ihrem Computer noch nicht vorhanden sind (meine Programme nicht funktionieren), können Sie diese dll´s hier downloaden (ca. 1,3 MB). Danach msvbvm50.exe starten (doppelklicken). Die dll´s werden dann automatisch in das Windows-Systemverzeichnis Ihres Computers kopiert.
Die Programme funktionieren nur unter der Bildschirmauflösung 800*600 (und größer), auf die Ihr Computer eventuell noch umgestellt werden muß.
Die Datei "bm.exe" nach Runterladen auf Ihren Computer in ein einziges Verzeichnis (z.B. "c:\BewMath") kopieren und dann ausführen (Doppelklick auf "bm.exe" im Programmanager oder Explorer). Die selbstextrahierende Datei "bm.exe" wird dann in dasselbe Verzeichnis entpackt, so daß die einzelnen Programme des Programmpakets erscheinen. Danach kann "bm.exe" wieder gelöscht werden. Als Startprogramm "BewMath.exe" benutzen.
