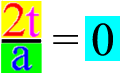
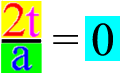
Vorweg:

1. bin ich auch nicht gerade ein Mathegenie,

2. ist jeder mal betriebsblind:

ich kann mich noch bestens erinnern, dass in meinem schriftlichen Abitur in einer Aufgabe zu berechnen war - eine Berechnung, die ich dann auch hübsch brav mit der damals noch üblichen Logarithmentafel durchgeführt habe und die bei mir 49,99 ergab.

Nun hätte man (?) ja wohl bittschön auf Anhieb "wissen" können (müssen?), dass exakt gleich 50 ist

(und sei´s, weil 5² = 25 ist),

d.h. man hätte sich also jegliche umständliche Rechnung (über Logarithmen) sparen können.

Spätestens aber dann, als bei mir 49,99 heraus kam, hätte ich doch "sehen" müssen, dass da wohl (wie bei Logarithmen üblich) ein Rundungsfehler vorlag und vermutlich 50 heraus zu kommen hatte.

Und dann wiederum hätte es bei mir "Klick" machen müssen, dass exakt gleich 50 ist - und ich mir jegliche Rechnung hätte sparen können.

Mein Mathelehrer hielt aber (mit einigem Recht!) das Ergebnis 49,99 für derart unschön, dass er allein deswegen die Note meiner Abiklausur von 1+ auf 1 gesenkt hat.

1. und 2. zusammen haben vielleicht den Vorteil, dass man leichter die "Begriffsstutzigkeit" vieler SchülerInnen versteht.

Angenommen mal, eine Aufgabe in einer Klassenarbeit würde schlichtweg lauten:

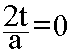
Nun wird sich ein Normalsterblicher (einE SchülerIn) vermutlich fragen:

"Wo - zum Teufel - ist da eigentlich die Aufgabe, d.h. was soll ich da eigentlich tun [Arbeitsanweisung] bzw. wonach ist da eigentlich gefragt?"

EinE MathematikerIn weiß aber bei einer Gleichung, in der auf der einen (hier rechten) Seite eine nackte Null steht, sofort, was zu tun ist: nämlich herauszufinden, wann die andere Seite (hier also links ) Null "wird".

Warum weiß einE MathematikerIn das?: weil sie/er gelernt hat, dass in sämtlichen Gleichungen dafür gesorgt werden muss

(wenn das nicht schon anfangs so ist),

dass auf der einen Seite Null steht - und dass dann das Ausrechnen erheblich einfacher ist.

Und schon drängt sich die nächste Frage auf: warum ist das Ausrechnen erheblich einfacher, wenn auf einer Seite eine Null steht?

Versuchen wir dazu mal, =  0  ansatzweise auf "klassische" Art zu lösen. Dazu stellen wir uns - immer ein guter Tipp! - möglichst dumm und deshalb als größte Schwierigkeit fest, dass links - igitt! - ein Bruch vorliegt. "Brüche können wir nicht", und deshalb muss der Nenner a weg. Bislang wird durch ihn geteilt, und um das "rückgängig" zu machen, tun wir das glatte Gegenteil, d.h. wir multiplizieren mit a - und zwar (wohlgemerkt!) hübsch beide (!) ganzen (!) Seiten der Gleichung:

              =  0           | ● a

      ● a =  0  ● a

Dabei ist es hier eher unwichtig, dass

• im nächsten Schritt links nur der ehemalige Zähler 2t stehen bleibt,

• also dort der Nenner das a futsch ist,

• wir also unser Ziel erreicht haben, den "schwierigen" Bruch links zu eliminieren.

Sondern uns interessiert hier nur, was rechts passiert. Dort steht  0  ● a und das ist - egal für welches a - immer Null, d.h. rechts brauchen wir überhaupt nicht mehr zu rechnen.

Kleines Intermezzo:

Das "Problem" 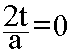ergab sich in einer Klassenarbeit nach längerer Rechnung, und der Lehrer, der die Klassenarbeit gestellt hatte, war entsetzt, dass viele SchülerInnen nicht mal "sowas Einfaches" lösen konnten.

(Nebenbei: eine zentrale Schwierigkeit lag für viele SchülerInnen vielleicht einfach darin, dass die Variablen "t" und "a" hießen und nicht - wie sonst andauernd im Mathematikunterricht - "x" und "y": "Wo kommen wir da denn hin, wenn die Variablen auch variable Namen haben?!")

Denn eigentlich sollten die SchülerInnen doch problemlos folgende (jetzt vollständige) Standardrechnung durchführen können:

              = 0          | ● a

    ● a = 0 ● a

     2t        = 0         | : 2

       t        = 0

(Nebenbei: auch hier am Ende zeigt sich wieder, wie schön es ist, wenn links eine Null steht, denn Null durch irgendwas [hier 2] ist immer Null, d.h. auch hier brauchen wir überhaupt nicht mehr zu rechnen.)

Fassen wir also zusammen: die linke Seite "wird" Null, wenn (auch) t =  0  ist.

Nun wundert es mich überhaupt nicht, wenn so einige SchülerInnen gerade das (scheinbar) Allereinfachste nicht können: genau da zeigt sich, ob jemand Grundsätzliches (nicht) verstanden hat - nämlich hier die Funktionsweise von Brüchen.

Schauen wir uns dazu mal an, wie einE MathematikerIn die Gleichung 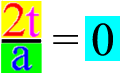lösen würde:

1. macht er sich zu allererst klar, dass

• links ein Bruch, nämlich , steht

• und rechts eine  0  (s.o.).

2. Beim Bruch denkt unserE MathematikerIn geradezu zwanghaft als allererstes daran:

der Nenner (hier  a  ) darf niemals Null sein, denn "durch Null darf man nicht teilen".

Oder anders gesagt: der Nenner (hier  a  ) darf alles sein, nur nicht 0 .   *

3. ist aber der Nenner letztlich völlig egal, sondern ein Bruch ( hier ) kann nur Null "werden", wenn der Zähler (hier  2t  ) Null "wird".

4. Nun "wird" aber  2t  nur dann Null, wenn t = 0 "wird".
   (In umgekehrter Analogie zu * könnte man also sagen: t darf nichts sein außer 0.
    t kann also nur den einen Wert 0 annehmen, a hingegen alle Werte außer 0.)

Ich hoffe also, dass die (scheinbar) simple und blödsinnige Gleichung 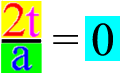geeignet ist, an ihr fundamentale mathematische Fähigkeiten aufzuzeigen bzw. diese zu vermitteln.

Nur ein weiteres Beispiel für ach so Einfaches, was viele SchülerInnen nicht können:

wenn sie eine Gleichung der Form 0 = x² - x bekommen, stehen sie völlig auf dem Schlauch, denn sie können "nur" viel kompliziertere Gleichungen der Form 0 = x² + px + q lösen.

Sie können

(wie jahrhundertelang die Menschheit!)

auch nicht das Nichts ergänzen

(wieso sollte man auch?!)

und es mit Null identifizieren:

0 = x² - x =

  = x² - x + Nichts =

  = x² - x +    0 ,

worauf ja durchaus die allseits bekannte p-q-Formel zur Lösung von 0 = x² + px + q anwendbar ist, da hier q =  0

 (und [auch nicht deutlich sichtbar] p = 1).

Der Grund, warum viele SchülerInnen wohl das Schwierige, nicht aber das Einfache können, liegt natürlich darin, dass andauernd nur das Schwierige durchgenommen und dann so lange sinn- und verstandlos gebimst wurde, bis auch der Letzte (?) es anwenden konnte.

Nicht aber verstanden wurde, erstens, die "Struktur" von 0 = x² - x :

1. , dass links wieder mal die beliebte Null auftaucht,

2. , dass rechts in beiden Summanden x auftaucht (also sowohl in x² als auch in x),

3. , dass also

•                                                       x²      für x =  0  Null "wird"

• und                                                       x für x =  0  Null "wird",

• insgesamt also auch der Gesamtterm x² - x für x =  0  Null "wird".

Da hat man wieder ohne jede großartige Rechnung, sondern "einfach nur" durch Nachdenken die Lösung.

Oder genauer: man hat mit x = 0 (immerhin!) eine der beiden Lösungen

(und an eine mögliche zweite denkt man wohl nur, wenn man

• ein grundsätzliches Verständnis quadratischer Funktion

• und von deren Graphen [möglicherweise zwei Nullstellen] hat).

Zweitens nämlich "sehen" viele SchülerInnen nicht, dass x in beiden Summanden vorkommt

(und kein "absolutes Glied" q vorkommt),

also das

(sowieso längst vergessene und nie wirklich verstandene)

Distributivgesetz anwendbar ist:

       0  =  x² - x

   0  = (x  - 1 ) • x

Und sie wissen nicht, dass ein Produkt nur dann Null ergeben kann, wenn einer der beiden Faktoren Null ist, hier also, wenn

1. entweder  x - 1         =  0  

2. oder                     x  =  0  ist.

(Nebenbei: dieser Trick funktioniert wieder nur, wenn auf der anderen Seite der Gleichung  0  steht!)

Die zweite Lösung, also x =  0 , hatten wir ja auch schon oben herausgearbeitet.

Und an x - 1 =  0  sollte (?) man eigentlich (ohne Rechnung) "sehen", dass das für x = 1 (die zweite Lösung) funktioniert.

Es gibt - nebenbei - noch einen anderen, vielleicht sogar noch eleganteren Lösungsweg:

wenn man   0  =  x² - x zu x = x² umformt, erkennt man evtl. schnell:

0 und 1 sind die einzigen Zahlen, deren Quadrat wieder die Zahl selbst ist. Somit gilt natürlich

1.    0 = 0²

2.    1 = 1²