man muss nicht alles können

Grundlage des üblichen Matheunterrichts ist allerdings das glatte Gegenteil: SchülerInnen sollen

1. zur Lösung eines (für sie) neuen Problems aus dem Vorunterricht sämtliche notwendigen Voraussetzungen haben,
2. dieses Problem vollständig lösen können.

 Dahinter stehen wohl zwei Grundideen:

1. das Bild von einer rein deduktiven, streng aufeinander aufbauenden Mathematik

(vgl. Euklid bis Weierstrass ...),

2. dass SchülerInnen nicht dadurch frustriert werden sollen, dass sie Sachen nur halb verstehen.

Die Folge des "Vollständig-Verstehens" ist aber, dass die übliche Schulmathematik

• strikt linear ist : ...

(mit der fatalen Folge, dass Aussetzer sich später gnadenlos rächen),

• immer nur uralte Mathematik durchgenommen wird

(schließlich muss schneckenhaft langsam ein Großteil der Mathematikgeschichte nachgekaut werden),

• keine vom strikt linearen Lehrplan abweichenden Probleme auftauchen und
• insgesamt alles arg verlässlich ist, aber eben deshalb auch schnarchlangweilig bleibt.

Und überhaupt wird im üblichen Unterricht immer wieder deutlich, dass ja bereits die beiden Prämissen 1. und 2. nicht stimmen:

1. haben SchülerInnen oftmals eben nicht (mehr) alle notwendigen Voraussetzungen aus dem Vorunterricht parat

(was nebenbei oftmals eine gigantische Fülle wäre),

bzw. diese wurden zwar "irgendwann in grauer Vorzeit" mal durchgenommen, aber doch längst wieder vergessen.

(Manchmal, wenn die SchülerInnen wieder mal alles Vorwissen vergessen haben

[und nur dann, wenn ich selbst sie im Vorjahr unterrichtet habe],

frage ich sie gerne ironisch: "Welche Pfeife hattet ihr denn letztes Jahr als Mathelehrer?"

Ein netter Schülertrick besteht nebenbei darin, selbst dann, wenn sie das bei einem anderen Lehrer erworbene Vorwissen teilweise noch haben, dies dennoch zu leugnen, denn dann fühlt der "neue" Lehrer sich aufgerufen, es nochmals zu erklären.)

2. wird zwar üblicherweise und im fragend-entwickelnden Unterricht und an der Tafel die vollständige Lösung eines "Problems" vorgemacht, zeigt beispielsweise die nächste Klassenarbeit aber, dass viele SchülerInnen diese Lösung eben nicht verstanden haben und also auch nicht reproduzieren können.

(Es ist doch eine geradezu typische Lehrererfahrung: der Vorunterricht lief doch scheinbar so gut [alle hörten zu bzw. schwiegen], und erst in der Klassenarbeit [also zu spät] merkt man voller Überraschung, wie wenig so einige SchülerInnen verstanden haben.)

Meine These hier ist, dass man durchaus mal Probleme durchnehmen sollte,

• die vom linearen Fortgang abweichen

(insbesondere kann, ja sollte man das ab und zu tun, wenn ein "späteres" Thema schon in der Luft liegt

[also beispielsweise bei der Behandlung der Brüche die Nicht-Brüche, d.h. irrationalen Zahlen]

oder wenn aus der "Vogelperspektive" durchaus ein Zusammenhang zu einem scheinbar abgelegenen, in Wirklichkeit aber instruktiven Thema naheliegt

[also beispielsweise beim Satz des Pythagoras der letzte Satz von Fermat; vgl. ]),

• für deren Lösung nicht sämtliches notwendige Vorwissen vorhanden ist
• und die auch nicht vollständig lösbar sind.

Einfachste Beispiele sind da Ausblicke in die

(SchülerInneN ansonsten systematisch vorenthaltene)

aktuelle Mathematik, also in Probleme, die wahrhaft "hardcore" und selbstverständlich nicht vollständig von SchülerInneN (und LehrerInneN!) lösbar sind wie etwa - nochmals -

Ein weiteres Beispiel sei die (Taylor-)Reihenentwicklung des Logarithmus, also

   ,

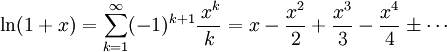ergänzt durch die kleine Hilfsgleichung

.

Ich kann und will hier nicht vollständig ausführen, wie eine komplette Unterrichtseinheit dazu aussehen könnte.

Soviel aber doch immerhin:

1. halte ich solch eine Unterrichtseinheit durchaus schon in einer 10. Klasse für möglich, denn dort ist der Logarithmus ja (erstmals) ausdrücklich Thema; oder umgekehrt: die Unterrichtseinheit ist nicht erst in der Oberstufe möglich, wenn also (falls überhaupt) die e-Funktion und der natürliche Logarithmus Thema sind;
2. das benötigte Vorwissen:

Grundkenntnisse über den Logarithmus; insbesondere sollten die SchülerInnen

• die Formel zwar nicht für den natürlichen, aber doch beispielsweise für den Zehnerlogarithmus verstanden haben und also wissen,
  • dass man mit dieser Formel den Logarithmus einer Zahl > 1 in einen einer Zahl < 1 umrechnen kann,
  • es also reicht, Logarithmen von Zahlen < 1 berechnen zu können;
• wissen, dass sich die Logarithmen zu verschiedenen Basen (im folgenden a und b) mittels der Formel ineinander umrechnen lassen, dass also insbesondere
  • jeder Logarithmus zu einer anderen Basis (z.B. der Basis 10) in einen natürlichen Logarithmus überfährt werden kann
  • und es somit reicht, natürliche Logarithmen berechnen zu können.

Bzw. die beiden genannten Formeln müssen ja nicht mal vorher durchgenommen worden sein, sondern können erst anlässlich der Bearbeitung von hergeleitet werden.

3. Was die SchülerInnen nicht wissen müssen und auch in der hier angedachten Unterrichtseinheit nicht lernen:

• was genau die Zahl "e" und damit auch der natürliche Logarithmus ist;
• wie die Formel bewiesen wird

(immerhin wäre aber ein Exkurs denkbar, wie man überhaupt darauf gekommen ist),

• weshalb auf der linken Seite dieser Formel 1+ x statt - wie doch eigentlich zu erwarten und viel praktischer? - nur x auftaucht,
• eine "saubere" Behandlung der Konvergenz

(Konvergenzkriterien, ε ...).

Ich habe die Erfahrung gemacht, dass sich (einige) SchülerInnen durchaus dafür interessieren, wie man denn überhaupt Logarithmen berechnen kann: als ich zu Beginn einer Unterrichtseinheit über Logarithmen mal dreist und ein wenig provokativ

"entnehmt die Logarithmen dem Taschenrechner und glaubt sie einfach"

sagte, kam in einer Klasse geharnischter Widerspruch!

Mit 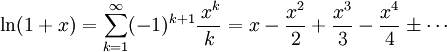haben wir etwas, was in Schulen kaum mehr vorkommt, nämlich eine sogenannte "Reihe".

Dafür , dass die Reihen kaum (mehr) in Schulen vorkommen, gibt es durchaus gute Gründe:

1. anderweitiger (immer größerer) Stoff- sowie der Klausurdruck

(man hat ja kaum mehr Zeit für "Ausflüge")

2. wenige "Anwendungsmöglichkeiten" in der gängigen Schulmathematik,
3. Reihenberechnungen sind

(insbesondere bei schwacher Konvergenz)

frustrierend aufwendig, wenn man sie noch selbst durchführen möchte/soll

(also zwar mit einem Taschenrechner, aber ohne programmierbaren Computer),

4. Reihen erfordern ein vermutlich doch schon erhebliches Abstraktionsvermögen,
5. Reihen mögen früher

(eben zum Beispiel zur Berechnung von Logarithmen)

noch wichtig bzw. unvermeidlich gewesen sein, scheinen aber überflüssig, wenn man einen Computer zur Hand hat

(und da ist es unerheblich, ob der Computer eventuell intern auch mit Reihen und Logarithmen rechnet).

Ich meine dennoch, dass Reihen auch im Zeitalter des Computers interessant sind - und vielleicht sogar noch interessanter werden. Denn da man die Näherung ja vom Computer durchführen lassen

(und die sukzessive Annäherung dabei schön beobachten)

kann, kann man sich viel mehr auf das Prinzip konzentrieren

(... und das entsprechende Programm selbst schreiben?

So ganz vertraue ich dem Computer allerdings doch nicht: man sollte auch mal eine Reihenberechnung "von Hand" durchgeführt haben, um

• überhaupt erst den Computer schätzen zu können, statt ihn als selbstverständlich vorauszusetzen,
• mittels dieser Berechnung auch das Prinzip besser verstehen zu können.)

Das Prinzip aber, nämlich die sukzessive Annäherung, ist allemal elementar wichtig für den Matheunterricht, denn man könnte es (in einer 10. Klasse) als "Limespropädeutik" bezeichnen.

Dabei ist die Abstraktion (vgl. 4.) nicht ein (unnötiger/unvermeidlicher?) Betriebsunfall, sondern geradezu Sinn und Zweck

(beispielsweise in Endform, dass die Tangente an einen "krummen" Graphen nicht durch Sekanten angenähert, sondern erst als Limes der Tangenten definiert wird),

denn

Mathematik IST Abstrahieren!

Wenn der Logarithmus einer Zahl nicht gerade offensichtlich, weil eine natürliche Zahl ist

(z.B. log ₃ 81 = 4, denn 3⁴ = 81),

so ist er vermutlich schaurig irrational, und zudem lassen sich Logarithmen nicht

(das kann man SchülerInnen nur mitteilen)

mit einfach-endlichen Gleichungen bestimmen, sondern immer nur annähern.

Die erste Möglichkeit zu solch einer Annäherung bestünde im Ausprobieren

(u.a. unter Zuhilfenahme eines Taschenrechners),

aber das wäre doch arg unsystematisch und also umständlich. Schöner wäre eine - wenn auch nicht endliche - systematische Formel, mittels derer man dann z.B. auch einen Computer an die Arbeit setzen könnte.

Und solch nicht-endliche Formeln wären eben unendliche Reihen.

(Nebenbei: keine Ahnung, wie Computer Logarithmen ermitteln, aber ich vermute mal, dass sie das intern-unsichtbar eben auch mit Reihen tun.)

Der Vorteil solcher Reihen - wenn es sie denn gibt - wäre zudem, dass man den gesuchten Wert zwar nie exakt erreicht, aber doch  beliebig genau annähern kann.

Nochmals: hier sei nicht detailliert aufgezeigt, wie eine Unterrichtseinheit zur Reihenentwicklung des Logarithmus aussehen könnte, sondern nur angedeutet, was wünschenswert und wohl auch machbar wäre:

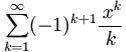• sieht zwar erstmal scheußlich hochkompliziert aus - und ist in Wirklichkeit doch eine feine Sache, weil eine kurze (endliche!) Schreibweise für den unendlichen Ausdruck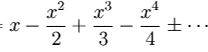
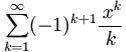• Im Unterricht müsste erarbeitet werden, was eigentlich bedeutet, nämlich

=

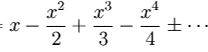• Diese Schreibweise hat, obwohl sie unendlich ist, aber durchaus ihrerseits ihre Vorteile gegenüber 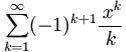, denn man sieht an 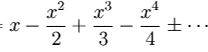wohl deutlicher die Systematik:
  • das Alternieren der Vorzeichen, also + , - , +, - , + , - , ...
  • die simple Reihenfolge der Zahlen 2, 3, 4,
  • dass diese jeweils sowohl im Zähler als auch im Nenner auftauchen.
• Durchprobieren mit konkreten (einfachen!) Zahlen für x sowie einigen wenigen Summanden zeigt schnell, dass die Reihe

• für x > 1 divergiert, also unbrauchbar ist,

(und da dann eben braucht man, wie oben schon angedeutet, ggf. )

• für x < 1 konvergiert

(was, wie oben ebenfalls schon angedeutet, nicht bewiesen werden soll).

Zwar kann man durch eigenhändiges Rechnen schnell diese Konvergenz bzw. Divergenz zeigen, aber für das weitere Verhalten (auch die Schnelligkeit der Konvergenz) wäre doch ein leicht schreibbares Computerprogramm sehr hilfreich.

• Dieses Konvergieren müsste man sich auch mal anschaulich machen:

(die Schallwelle dringt in einen Trompetentrichter ein)

Entsprechend sähe Divergieren so aus:

(der Schall kommt aus einem Trompetentrichter heraus)

Überhaupt sind mir solche bildlichen Vorstellungen ungeheuer wichtig, und es wäre viel getan, wenn die SchülerInnen "nur" sie behalten würden.

Nebenbei kann man mit dem Trompetenbild auch schön

• langsame Konvergenz
• und schnelle Konvergenz

unterscheiden.

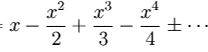• Anhand des Trompetenbildes wird auch deutlich, wodurch die Konvergenz von maßgeblich erzeugt wird, nämlich dadurch, dass
  • wegen der alternierenden Vorzeichen einer Auf- immer eine Abbewegung (vgl. ) folgt,
  • für x < 1 die Brüche (Auf- und Abbewegungen) immer kleiner werden.
• Es würde sich allemal lohnen, mindestens noch zwei andere Reihen anzusehen, nämlich

1. , die, obwohl sie sich nur aufwärts bewegt, erstaunlicherweise dennoch konvergent ist,
2. die vermutlich einfachste, sogenannte "harmonische" Reihe , die im Gegensatz zu 1. nicht konvergent ist, wozu man auch den hübsch intelligenten Beweis durchnehmen könnte:

Und dem müsste ein (anschaulicher, nicht streng mathematischer) Vergleich von 1. und 2. folgen:

1. in 1. werden die Summanden hinreichend schnell kleiner,

2. in 2. werden sie zu langsam kleiner.

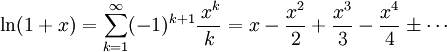• Am erstaunlichsten finde ich aber, dass überhaupt funktioniert, dass also der Logarithmus als (wenn auch unendliche) Summe sehr einfacher und regelmäßiger Terme

(die allesamt nichts mit dem Logarithmus am Hut haben)

darstellbar ist

(wenn auch mit dem kleinen Schönheitsfehler, dass das nicht für ln (x), sondern nur für ln (1 + x) funktioniert).

Ich halte die Reihenentwicklung des Logarithmus

• zwar allemal für (auch schon in einer 10. Klasse) unterrichtsgeeignet,
• aber nur in Grenzen für klassenarbeitsgeeignet.

Und damit wird sie wegen des Stoff- und Klassenarbeitsdrucks wohl leider "hinten runter fallen".