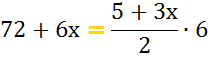 nach
x auflösen
nach
x auflösen
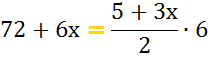 nach
x auflösen
nach
x auflösen
Vorweg zur Fachsprache
(damit wir uns
besser über
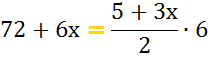 unterhalten
können):
unterhalten
können):
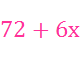 und
und 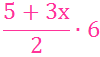 .
.| links ein Term (z.B. 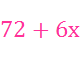 ), ), |
|||
| rechts ein Term (z.B. 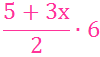 ), ), |
|||
| dazwischen
ein Gleichheitszeichen, |
insgesamt also z.B.
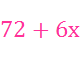 |
= | 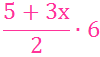 |
(normalerweise ist es dabei das Ziel, einen schwierigen Term Tschwierig über mehrere Zwischenschritte in einen möglichst einfachen Term Tganz einfach zu überführen, wobei sich dann paradoxerweise doch eine Gleichungskette ergibt:
Tschwierig = Teinfacher = Tnoch einfacher = ... = Tganz einfacher),
Im Laufe der Schulzeit tauchen (leider) massenhaft Gleichungen auf, die zu "lösen" sind
(hier nicht betrachtet seien die folgenden beiden durchaus möglichen Fälle:
Wenn überhaupt, so ist eine Gleichung nur dann lösbar, wenn nur noch eine einzige Unbekannte in ihr vorkommt
(sonst liegen keine Unbekannten, sondern voneinander abhängige sogenannte "Variablen" vor).
Im vorliegenden Fall
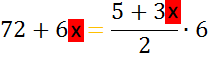 ist
x diese (einzige)
Unbekannte.
ist
x diese (einzige)
Unbekannte.
"Unbekannte"
ist dabei eine Abkürzung für "eine anfangs noch
unbekannte
Zahl", die aber durch verschiedene Umformungen am Ende
herausgefunden werden soll, dann also endlich
nicht mehr unbekannt ist. Diese dann bekannte
Zahl nennt man auch "Lösung" der anfänglichen Gleichung.
(denn die Zahl, die wir ganz am Ende nach allen Rechnungen finden, muss natürlich die Gleichung ganz am Anfang lösen
[und deshalb kann eine Probe nie schaden, wobei "Probe" heißt, die am Ende gefundene Zahl für die Unbekannte in der allerersten Gleichung einzusetzen und zu schauen, ob diese erste Gleichung auch tatsächlich mit der eingesetzten Zahl "funktioniert"]).
Die letzte Gleichung beim Lösen von Gleichungen sieht
(wenn die Unbekannte x heißt)
immer
Zahl = x
x = Zahl.
In beiden Fällen wissen wir dann endlich, welche Zahl hinter der lange Zeit Unbekannten x verborgen war.
Unser Ziel ist es also immer,
entweder auf der linken Seite der Gleichung
oder aber auf der rechten Seite der Gleichung
nur noch das nackte
 ohne
jegliche
sonstigen
ohne
jegliche
sonstigen
 zu haben
zu haben
(wer
will z.B. schon wissen, was
3
 kosten, wenn er sich gerade mal eben nur
kosten, wenn er sich gerade mal eben nur
 leisten kann?).
leisten kann?).
Das heißt aber, dass ausnahmslos alle sonstigen Zusätze, die lange Zeit links oder rechts stehen, dort Schritt für Schritt gnadenlos beseitigt werden müssen.
Eine Gleichung zu lösen, in der x vorkommt, heißt also, sie auf einer Seite zum nackten x hin "aufzulösen".
Angenommen mal, dass die Unbekannte x am Ende rechts stehen, die letzte Zeile also so
Zahl = x
aussehen soll.
Dann sehen die Gleichungsumformungen immer so aus:
Das Das⇔-Zeichen
(auch "Äquivalenzzeichen" genannt)
symbolisiert dabei, dass die jeweils vorherige und die folgende Gleichung "äquivalent" (deutsch: gleichwertig) sind, womit gemeint ist, dass die Lösung unverändert bleibt
(was auch bedeutet, dass keine Lösung hinzukommt oder verschwindet).
Nur so kann man sich sicher sein, dass die Zahl, die ganz am Ende herauskommt, auch tatsächlich die Anfangsgleichung löst.
Um diese durchgehende Äquivalenz zu bewahren, darf man nur sogenannte "Äquivalenzumformungen" durchführen. Wie diese aussehen, wird weiter unten geklärt.
Vorsicht: man kann bei Gleichungsumformungen das Äquivalenzzeichen natürlich immer ganz stumpf dem Lehrer zuliebe hinschreiben, aber das ist grob falsch, wenn man nicht auch korrekte Äquivalenzumformungen durchführt.
Nun können wir endlich zur Lösung von
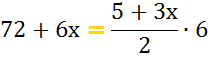 schreiten.
schreiten.
In
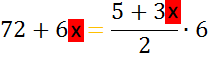 taucht die
(einzige!)
Unbekannte
x
auf
beiden Gleichungsseiten
auf. Wir haben die freie Wahl, ob sie am Ende nur noch links
oder nur noch rechts auftauchen soll - und entscheiden uns
hier mal dafür, dass
x
nur noch
rechts auftauchen soll.
taucht die
(einzige!)
Unbekannte
x
auf
beiden Gleichungsseiten
auf. Wir haben die freie Wahl, ob sie am Ende nur noch links
oder nur noch rechts auftauchen soll - und entscheiden uns
hier mal dafür, dass
x
nur noch
rechts auftauchen soll.
Zuerst wollen wir schrittweise
erreichen, dass
rechts nur noch
x
steht, und fragen uns daher, was auf der rechten Seite noch
stört. Das ist
offensichtlich
alles außer
eben dem
x
:
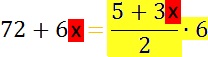
"alles" ist aber ein bisschen arg viel auf einmal
(da sieht man ja vor lauter Bäumen den Wald nicht mehr, d.h. man weiß gar nicht, wo man anfangen soll),
und deshalb zerlegen wir dieses "alles" in in seine einzelnen Bestandteile
(jetzt mal vergrößert, damit man die Bestandteile besser erkennt):

Die störenden Einzelbestandteile der rechten Seite sind also
 ,
,
![]() bzw.
bzw. ![]() , denn
, denn ![]() ist ja eine
Kurzschreibweise für
ist ja eine
Kurzschreibweise für ![]() ,
,
![]() ,
,
![]() .
.
(Sehen wir mal davon ab, dass man sofort die 6 gegen die 2 kürzen könnte, wobei 3 herauskäme und schon das Fieseste an der ganzen Gleichung, nämlich der Bruch, beseitigt wäre.
Die meisten Schüler würden diese Kürzungsmöglichkeit nämlich gar nicht sehen, weil die 6 und die 2 nicht in einem Bruch auftauchen.)
Die störenden Einzelelemente wurden hier erstmal in willkürlicher Reihenfolge aufgezählt. Damit stellen sich zwei Fragen:
: ist es egal, in welcher Reihenfolge wir sie auf der rechten Seite beseitigen? Und wenn nicht:
: welche Reihenfolge ist denn die richtige bzw. "einzig wahre"?
Es sei hier nicht begründet, weshalb es nicht egal ist, in welcher Reihenfolge die störenden Einzelelemente auf der rechten Seite beseitigt werden, sondern nur kategorisch festgestellt, dass es nicht egal ist.
Damit stellt sich automatisch nochmals die Frage B. nach der richtigen Reihenfolge. Ein guter erster Tipp ist da:
| es wird immer das zuerst beseitigt, was am weitesten von x entfernt ist. |
Dabei ist "am weitesten entfernt" oftmals, aber leider nicht immer räumlich gemeint. Z.B. ist in

![]() räumlich weiter
entfernt von x als
räumlich weiter
entfernt von x als
![]() , muss im
Laufe der Rechnungen
, muss im
Laufe der Rechnungen ![]() also
vor
also
vor ![]() beseitigt werden.
beseitigt werden.
Aber
![]() ist auch
räumlich
weiter entfernt von x
als
ist auch
räumlich
weiter entfernt von x
als ![]() , und dennoch muss
, und dennoch muss
![]() nach
nach
![]() beseitigt
werden.
beseitigt
werden.
Was also bedeutet "am weitesten entfernt" in jenen Fällen, in denen es nicht räumlich gemeint ist?
Die erste Antwort, nämlich "rechnerisch am weitesten entfernt", ist da nicht gerade hilfreich.
Ein zweiter guter Tipp ist da:
| man setze für x
probeweise eine beliebige einfache Zahl ein (dise willkürlich
gewählte Zahl
ist nicht automatisch schon die gesuchte Lösung der Gleichung !!!)
und rechne (zwangsläufig) von dieser Zahl ausgehend die jeweilige Gleichungsseite aus. |
Im vorliegenden Fall setzen wir in die rechte
Gleichungsseite
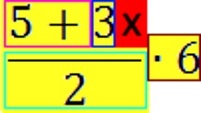 für
x z.B.
die
1 ein
und erhalten
für
x z.B.
die
1 ein
und erhalten
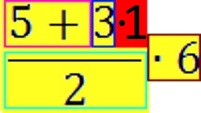 .
.
müssen wir zwangsläufig mit ![]() =
= ![]() beginnen und erhalten
beginnen und erhalten 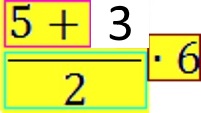 .
.
müssen wir nun zwangsläufig ![]() =
= ![]() rechnen
und erhalten
rechnen
und erhalten 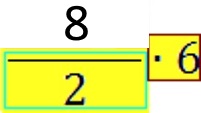 .
.
ist der nächste Rechenschritt
zwangsläufig  =
= ![]() , womit wir
, womit wir ![]() erhalten.
erhalten.
bleibt uns nun nur noch, ![]() =
= ![]() zu
rechnen.
zu
rechnen.
(Vorsicht:
auch dieses Ergebnis
![]() ist nicht
automatisch die gesuchte Lösung der Ausgangsgleichung
ist nicht
automatisch die gesuchte Lösung der Ausgangsgleichung
 .)
.)
Kurz gesagt sind die nötigen Rechenschritte (in dieser Reihenfolge):
![]() ,
,
![]() ,
,
 ,
,
![]() .
.
So gesehen ist
![]() rechnerisch
(!) am nächsten an x und
rechnerisch
(!) am nächsten an x und
![]() am weitesten
von x entfernt.
am weitesten
von x entfernt.
Da wir laut dem ersten Tipp immer mit dem jeweils Entferntesten anfangen, müssen wir die störenden Einzelelemente also in umgekehrter Reihenfolge beseitigen:
| unser Arbeitsprogramm (für die Säuberung der rechten Gleichungsseite):
|
 "Hau weg den Scheiß!" |
Legen wir also endlich los:
: das rechts
störende ![]() wird beseitigt:
wird beseitigt:
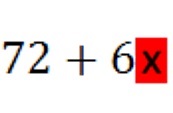 =
=  |:
6 (da bislang mit 6 multipliziert
wurde)
|:
6 (da bislang mit 6 multipliziert
wurde)
⇔(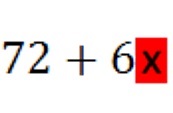 ):
6
=
):
6
=

Dabei besagt ein Balken | hinter einer Gleichung, dass die direkt hinter diesem Balken stehende Rechnung
(im vorliegenden Fall : 6 )
mit BEIDEN (!) GANZEN (!) Seiten der Gleichung durchgeführt werden muss
(genau
dann spricht man von einer "Äquivalenzumformung" [s.o.], und nur dann
bleibt die
Gleichung wirklich eine
Gleichung bzw. "in der
Waage":  ;
;
hingegen ist eine Ungleichung genauso wenig aussagekräftig wie eine Waage, bei der die beiden Schalen verschieden hoch stehen: da kann man nur sagen, dass eine Seite "irgendwie" schwerer ist als die andere, aber nicht herausfinden, wieviel eine Seite genau wiegt).
Im vorliegenden Fall
heißt "GANZE Seite" im Hinblick auf die linke Seite, dass der
komplette
Term
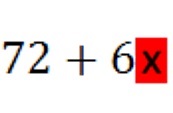 durch
6 geteilt
werden muss, also
durch
6 geteilt
werden muss, also
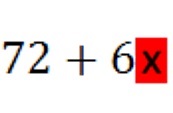 :
6
, würde aber fälschlich nur der zweite
Summand 6 x durch
6
geteilt.
:
6
, würde aber fälschlich nur der zweite
Summand 6 x durch
6
geteilt.
Das Fatale ist also, dass man hier ausnahmsweise mal
(von sich aus, also ohne Anweisung durch einen anderen!)
eine Klammer ergänzen muss - die gleich aber schon wieder beseitigt wird
("rin in die Kartoffeln, raus aus die Kartoffeln").
Man befolge die "Balken-Schreibweise"
(und viele Lehrer meinen die Vorschrift der Balken-Schreibweise tatsächlich als "Hilfe zur Selbsthilfe"):
(manchmal ist mir der Wille tatsächlich wichtiger als die Tat, denn ersterer erfordert oftmals tieferes Verständnis, während ein Rechenfehler eine lässliche Sünde ist).
Damit aber zurück zu
(72 + 6 x
): 6
=

⇔ 72 : 6
+ 6 x
: 6 =

⇔ 12
+
x
= 
 wird beseitigt - und damit wohl das Schwierigste an der Gleichung,
nämlich der Bruch:
wird beseitigt - und damit wohl das Schwierigste an der Gleichung,
nämlich der Bruch: | • 2
(da bislang durch 2 dividiert
wurde)
| • 2
(da bislang durch 2 dividiert
wurde)
24
+ 2 x
=
![]() |
- 5
(da bislang
5 addiert wurde)
|
- 5
(da bislang
5 addiert wurde)
⇔
19
+ 2 x
=
![]()
Jetzt könnten wir in einem 4. Schritt
noch auf beiden Seiten durch
3
teilen, um rechts auch noch die
3
zu beseitigen und damit unser Ziel zu
erreichen, nämlich rechts nur noch das nackte
x
stehen zu haben. Aber damit würden
wir
links fiese Brüche erhalten, nämlich
![]() und
und
![]() .
.
Da kümmern wir uns doch lieber erstmal um das Problem, dass x auf beiden Seiten der Gleichung auftaucht, aber nur rechts auftauchen soll. Also muss es links weg:
19
+ 2 x
=
![]() |
-
2 x
(da links bislang
2 x addiert wurde)
|
-
2 x
(da links bislang
2 x addiert wurde)
⇔ 19 = x ,
womit wir nun endlich unser
Ziel
Zahl
= x erreicht
haben: 19 ist
also die
Lösung der
Ausgangsgleichung
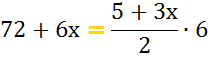 .
.
Anders gesagt: 19 war schon immer die (einzige) Lösung der Ausgangsgleichung, aber das war uns lange unbekannt und erst jetzt wissen wir Dummerchen das.