Heiner Stauff - anschauliche Mathematik

Mathematik nach dem dritten Bier
oder zwei Arten Mathematik

So etwa ab dem dritten Bier gibt ein Wort das andere und weiß hinterher keiner mehr, wie man eigentlich auf das jeweilige Thema gekommen ist.

Ich saß mit einem Freund (auch Mathelehrer) an einem lauen Sommerabend draußen vor einer Kneipe am Hafenkai in Münster, als sich nach dem dritten (?) Bier plötzlich "irgendwie" die Frage ergab:

Wie eigentlich schneiden sich zwei Zylinder?

(Haben "die" eigentlich keine anderen Sorgen?)

Der Einfachheit halber sei (vorerst) von zwei Zylindern ausgegangen, die einander senkrecht schneiden.

Der Freund traute sich nun auf Anhieb zu, die Schnittmenge der beiden Zylinder zu berechnen:

Ich wusste da nichtmal einen rechnerischen Ansatz, hatte aber sofort eine anschauliche Vorstellung von dieser Schnittmenge, die dem Freund eigener Aussage nach völlig fehlte

(was ja wohl auch heißt, dass ihm das rechnerische Ergebnis völlig unanschaulich bleiben würde):

"Unter Instrumentenflug versteht man das Fliegen, bei dem die Fluglage ohne Bezug auf äußere Anhaltspunkte ausschließlich mit Hilfe von Instrumenten kontrolliert wird. Gegensatz ist der Sichtflug."
(Quelle: )

Es liegt mir wahrhaft fern, nun meine anschauliche Art Mathematik besser zu finden oder gar als "eigentliche" Mathematik auszugeben:

spaltet sich die Menschheit wohl in eine anschaulich und eine abstrakt denkende Fraktion, und beide Fraktionen (unter SchülerInneN) müssen "Futter" bekommen

(mir scheint aber, dass erstere Fraktion gerade unter SchülerInnen bei weitem in der Mehrheit ist bzw. dass man zur zweiten Fraktion erst langfristig hinleiten kann);

vereinigt der ideale Mathelehrer vermutlich meine Fähigkeiten und die meines Freundes;
scheint mir doch, dass einem die Rechnung (und die Interpretation des rechnerischen Ergebnisses) leichter fällt, wenn man eine anschauliche Vorstellung vom Problem hat;
ist die Rechnung natürlich das eigentlich mathematische Fernziel;
bleibt aber die Anschauung ein Selbstzweck: und vollständig zu Ende rechnen können. Es ist eben auch schon "richtige" Mathematik, wenn man die Dinge im Kopf bewegen kann:

(Letztens hatte ich Mathematik in einem Klassenraum zu unterrichten, in dem nach einem Umbau noch die Tafel fehlte. Da dachte ich mir: "Mach´ doch aus der Not eine Tugend, also »Mentalgeometrie«." Und dann habe ich die SchülerInnen beispielsweise aufgefordert, rein im Kopf folgendes Dreieck um die rot markierte Seite rotieren zu lassen:

Das Ergebnis sei hier genannt, aber bewusst nicht gezeigt, sondern dem Kopf des Lesers überlassen: es kommt dabei ein Kegel heraus.

Diesen Kegel lassen wir nun - wieder nur im Kopf - vertikal um seine Spitze rotieren. Es entsteht - auch das sei wieder nur gesagt, nicht gezeigt - eine Art seitlich eingedelltes Rad.

Natürlich konnte ich in der betreffenden Stunde keine - wie man heute so schön sagt - "Evaluation" durchführen, aber mein Eindruck war: die einen konnten´s problemlos, die anderen gaben ganz schnell den Löffel ab.

Die Frage wäre aber doch, ob sich "sowas" trainieren ließe.)

Ich hatte für das Problem gleich eine sehr handgreifliche Veranschaulichung im Sinn, nämlich

ein "Kreuzstück",

wie es Sanitärfachleute beim Rohreverlegen benutzen.

Wohlgemerkt: ich habe also zu allererst an ein sehr praktisches und "alltägliches" Ding gedacht. Erst im zweiten Schritt folgte dann ein schon abstrakterer Gegenstand:

Und auch diesen Gegenstand abstrahiere ich nochmals weiter, indem ich die Enden der Rohre schließe, also den massiven Körper betrachte, und die beiden zylinderförmigen Rohre unterschiedlich farblich einfärbe.

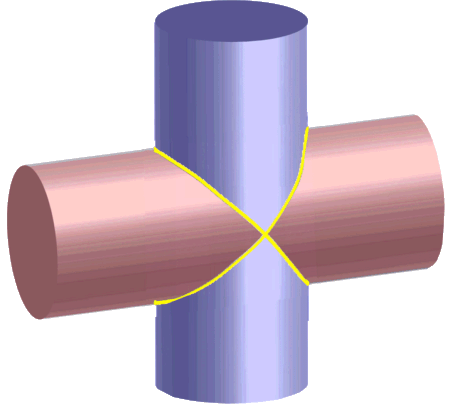
Hier nun liegt die "gefährliche" Täuschung nahe, dass man als Schnittmenge ansieht, was man von vorne sieht:

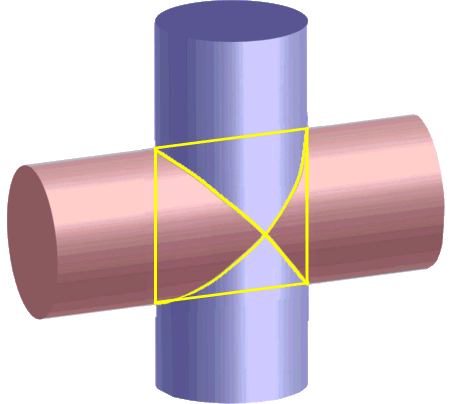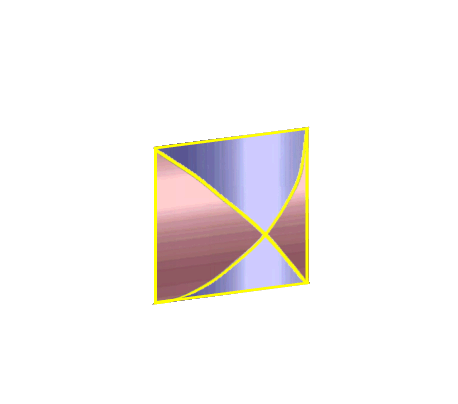
Genau (dreidimensional) genommen sieht das Teil, das wir da ausgeschnitten haben, nämlich so aus:

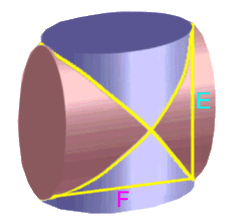
Und da stehen offensichtlich noch Teile (E und F) über, die nicht zur Schnittmenge der beiden Zylinder gehören.

Also trügt das Auge bzw. "lügt" das äußere (die Fassade) des Gegenstands. Hier sind also doch einige genauere Überlegungen nötig:

Die Oberseite A und die Unterseite B der Schnittmenge werden durch den roten Zylinder geliefert:

Die linke Seite C und die rechte Seite D der Schnittmenge werden durch den blauen Zylinder geliefert:

Die Schnittmenge der beiden Zylinder ist also, was in den beiden im Folgenden abwechselnden Zeichnungen gemeinsam ist:

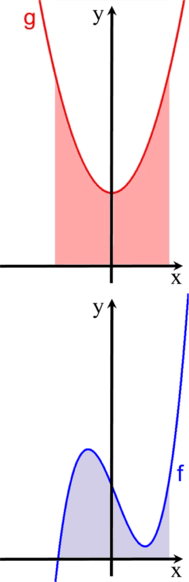
Die tatsächliche Schnittmenge sieht also so aus:

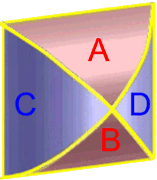
und nicht, wie oben erst vermutet, so:

Nun ist aber

trotz der Schattierung doch wieder notgedrungen nur eine zweidimensionale Projektion, an der das dreidimensionale, anschauliche Aussehen vielleicht schwer erkennbar ist.

Wegen der Unmöglichkeit, hier ein dreidimensionales Modell zu liefern, sei nur soviel angedeutet:

sieht die Schnittmenge von rechts ← und links → wie ein blauer Kreis aus,
sieht sie von oben ↓ und unten ↑ wie ein roter Kreis aus,
winden sich um die Schnittmenge zwei (hier hellgrün eingezeichnete) Ellipsen:

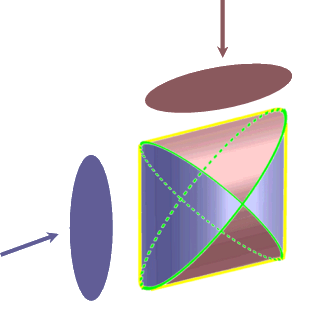
Wenn sich aber jemand das noch immer nicht vorstellen kann, dann sei ihm auf besonders süße Weise geholfen:

es gibt von der Firma Hussel eine Schokolade, die so aussieht:

Ein Einzelstückchen davon hat im Hinblick auf unser "Problem" zwei Nachteile:

den Rand, mittels dessen die Schokoladenstückchen untereinander verbunden waren

Also lassen wir diesen Rand kurzerhand verschwinden, indem wir ihn wegessen oder - schnöder - mit einem Bildbearbeitungsprogramm beseitigen:

(nebenbei: sogenannte "Schogetten" werden ja bereits in Einzelstücken geliefert und haben deshalb nicht diesen Rand; aber dafür passt ihre sonstige Form nicht zu unserem "Problem": sie sind oben zu sehr abgeflacht).

, dass das Einzelstückchen nicht quadratisch ist und deshalb ein "überflüssiges" Mittelstück enthält:

Aber auch hier helfen wir mit einem Bildbearbeitungsprogramm nach:

Und dann nehmen wir zwei solche Schokoladenstückchen, die wir mit den Unterseiten aufeinander pappen, was dann von der Seite so aussieht:

Ich habe noch immer keinen blassen Schimmer, wie man rechnerisch eine Gleichung für den Schnittknubbel

aufstellt.

Immerhin habe ich aber prompt im Internet gefunden, wie man sein Volumen berechnet :

Es wird das Volumen bestimmt, das durch Schnitt der beiden Zylinder

$\displaystyle Z_1:\ x^2+y^2\le r^2,\quad Z_2:\ x^2+z^2\le r^2$

entsteht.

Aufgrund der Symmetrie berechnet man zunächst das Volumen in einem Oktanten. Das Integrationsgebiet im ersten Oktant ist der Viertelkreis

$\displaystyle V:\ 0\le x\le r,\quad 0\le y\le \sqrt{r^2-x^2}.$

Die Funktion $h(x,y)=\sqrt{r^2-x^2}$ ist durch gegeben. Als Volumen ergibt sich

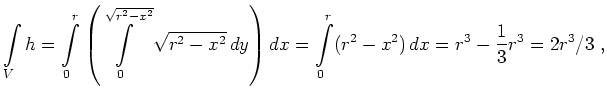
$\displaystyle \int\limits_V h=\int\limits_0^r\left(\int\limits_0^{\sqrt{r^2-x^2... ...-x^2}\,dy \right) dx=\int\limits_0^r(r^2-x^2)\,dx=r^3-\frac{1}{3}r^3=2r^3/3\ ,$

und damit als Volumen für den gesamten Körper .

Daran verstehe ich ja immerhin noch - jetzt, wo man´s mir sagt - die beiden Zylinderformeln $\displaystyle Z_1:\ x^2+y^2\le r^2,\quad Z_2:\ x^2+z^2\le r^2$ und weiß auch noch, dass man offensichtlich das "Raumintegral" der Schnittmenge berechnen muss, aber alles andere ist mir (abgesehen von gewissen Integrationsregeln) weitgehend unverständlich.

Eine ansatzweise Hilfe zu "unserem" Problem ist nebenbei auch . Und eine besonders schöne Visualierung der Schnittmenge habe ich glücklicherweise erst jetzt gefunden, nachdem ich selbst drauf gekommen bin: die Grafik 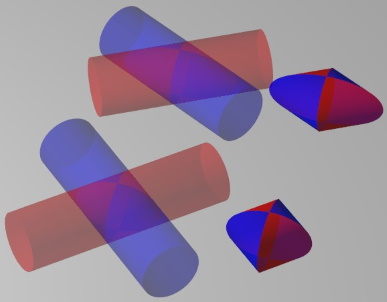im auch ansonsten aufschlussreichen Text .

Vergleich des weiteren :

"Stellt euch vor 2 identische Zylinder vor,deren Achsen rechtwinklig verlaufen.Diese bilden ein gemeinsames Schnittvolumen!Das volumen würde ich gerne mit Hilfe eines Integrales berechnen, so weit wo gut, jedoch kann ich mir dieses Gebilde nicht so recht vorstellen!!
[...]"

Nachdem diesem Fragesteller einiges erklärt und sogar eine Zeichnung der Schnittmenge geliefert worden ist

(bei der aber eben nicht klar ist, wie sie entstanden ist, ob sie also nur von einem Computer errechnet wurde),

muss er am Ende dennoch gestehen:

"mir fehlt wohl der 3D befehlssatz der meinem gehirn erlaubt solche sachen zu sehn :*( "

Dem Manne kann und muss geholfen werden, bzw. oder :

wenn die Schnittmenge gesucht ist, dann tue genau dies, nämlich selbst schneiden:
- knete den roten Zylinder aus Spielzeugknete oder einem Rührteig,
- stelle diesen Zylinder einige Zeit in den Kühlschrank, damit er ein wenig aushärtet,
- nimm eine runde Ausstechform (hier blau), wie man sie zum Plätzchenbacken benutzt, und schneide damit von oben die Schnittmenge aus dem roten Zylinder aus:

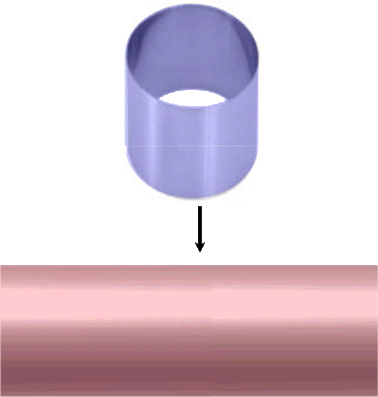
Oder man nehme ein Rundholz und bohre durch es mit einem Bohrer ein möglichst großes Loch (im Idealfall Bohrer- = Rundholzradius).

Man erhält dann allerdings nur ein Loch, also sozusagen das Negativ der Schnittmenge, das man dann aber beispielsweise mit Gips ausfüllen kann, von dem man hinterher das restliche Rundholz ablöst.

Oder man gehe den einfachsten Weg und nehme zwei

Klopapierrollen,

stelle/klebe die eine auf die andere

zeichne "perspektivisch" richtig, wie die obere die untere schneidet

schneide die entstehende Ellipse viermal so aus

klebe je zwei so zusammen

und klebe die beiden Doppelelemente so zusammen:

So richtig interessant wird´s aber erst z.B. bei

(wobei die Schweiß[?]- oder Guss[?]nähte eine schöne Hilfe sind).