Heiner Stauff - anschauliche Mathematik

Mathematik ist verdammte Disziplin

"Umfragen zeigen, dass nach wie vor neun von zehn Deutschen [ächt teutsche!] Tugenden wie Ehrlichkeit, Verlässlichkeit, Fairness, Fleiß, Disziplin, Treue, Respekt und Anstand für wichtig halten. Ein moderner, bürgerlicher Konservatismus ist im Kommen, auch und gerade unter Jüngeren [was im Hinblick auf mathematische Disziplin nur zu begrüßen wäre]."
(Berliner Kreis; Quelle:

)

"Disziplin ist eine Sekundärtugend, mit der man auch ein KZ betreiben kann."
(Oskar Lafontaine)

Vorweg:

geht es im Folgenden

nicht um die Mathematik als eine "Disziplin" im Sinne von "(Schul-/Studien-)Fach"

(dann müsste der Titel ja auch "Mathematik ist eine verdammte Disziplin" lauten),

sondern um Disziplin im Sinne von "Selbst(!)beherrschung"

(also zumindest nicht in erster Linie einer von außen [durch Lehrer, Eltern ...] erzwungenen Disziplin).

Ist das Teekesselchen "Disziplin" nur Zufall, oder braucht man Selbstdisziplin, um ein Fach zu beherrschen (!)?

zeige ich im Folgenden die Notwendigkeit von Disziplin auch und gerade in der Mathematik,

liefere ich aber keine pädagogischen Ansätze, wie die mathematische Selbstbeherrschung vermittelt werden kann.

(Am besten wäre es wohl, solche mathematische Selbstdisziplin als wünschenswert aufzeigen: dass sie also keine Schikane des Lehrers, sondern

[was allerdings immer eine autoritäre Unterstellung ist:]

"im wohlverstandenen eigenen Interesse" des Schülers ist:

dem Interesse, mit halbwegs akzeptablen Mathe-Noten durch die Schulzeit zu rutschen,

wenn's hoch kommt, dem Interesse an der Mathematik selbst.

Allemal wichtig scheint es mir aber zu sein, die mathematische Disziplin zu dosieren: viele und insbesondere jüngere Schüler können sich [noch] nicht eine ganze Schulstunde, also 45 Minuten lang

[oder im neuen "Doppelstundenmodell" sogar zwei Schulstunden lang]

konzentrieren

[ich habe mal irgendwo gelesen, die 45-Minuten-Schulstunde gebe es vor allem den Lehrern zuliebe, da 45 Minuten etwa der Konzentrationsdauer von Erwachsenen entspreche;

nebenbei: und dann sollen Schüler auch noch täglich sechs bis acht Schulstunden nacheinander höchst aufmerksam den Weisheiten der Lehrer lauschen!].

"dosieren" bedeutet für mich auch, nicht immer - wie üblich - "alles" auf einmal zu wollen, sondern ganze Unterrichtseinheiten zu den einzelnen Formen mathematischer Disziplin [s.u.] abzuhalten

[wenn auch nicht unter dem abschreckenden expliziten Titel "mathematische Disziplin"],

also z.B. mal stundenlang das farbige Unterstreichen [s.u.] mathematischer Informationen in Textaufgaben zu üben.)

Mit dem Thema "Disziplin in der Mathematik" wird's für meine Verhältnisse arg "spießig"

(ansonsten liegt mir ja eher die kreative und vor allem anschauliche Mathematik am Herzen).

Die Ausnahmen vorweg:

ich habe im Studium Mathe-Cracks erlebt, denen alles zuflog und die keinerlei Disziplin zu bedürfen schienen

(da habe ich erstmals neidlos entdeckt, dass ich "nur" gutes Mittelmaß bin).

Solche Cracks können sich dann z.B. auch eine völlig chaotische bis geradezu (zumindest für andere) unleserliche Schreibweise

leisten - weil sie sowieso alles längst im Kopf fertig haben

(so, wie Mozart seine Musik im Kopf komponiert hat und sie später nur noch schlechtgelaunt aufs Papier "kopieren" musste).

Mathematik ist oft "nur" Rumprobieren.

Aber auch dieses Rumprobieren bedarf einer gewissen Disziplin: dass man nicht nach wenigen Minuten aufgibt, sondern viel Zeit investiert, Durstphasen durchsteht und "Sitzfleisch" beweist

(und überhaupt Ehrgeiz und Interesse hat, ein Problem zu "knacken"):

das sind alles Voraussetzungen für jede Wissenschaft, aber auch z.B. für jedes gut ausgeführte Handwerk, wenn nicht gar für ein glückliches, weil engagiertes und kreatives Leben:

"Es gibt nichts Gutes, außer man tut es." (Erich Kästner)
(hier im Sinne von "man tut was")

Und solch ein Rumprobieren zeitigt oftmals

(wenn überhaupt)

nur dann Ergebnisse, wenn man schon viel weiß bzw. bereits viele Fertigkeiten hat, wenn man also

ahnt, in welche Richtung man "losprobieren" soll, und

Zufalls(?)ergebnisse einzuschätzen weiß:

Alexander Fleming,
"zufälliger" Entdecker des Penicillins

Ein Sonderfall ist die Schulmathematik: sicherlich gibt es Schüler, denen die Mathematik einfach "liegt".

Dem großen Rest kann ich nur sagen: natürlich könnt ihr jetzt ewig klagen und euch z.B. damit entschuldigen, dass in eurer Familie noch nie jemand Mathe konnte. Aber weil das nichts bringt, sondern nur eine "selbsterfüllende Prophezeiung" ist

(überhaupt erst dafür sorgt, dass alles schlecht wird),

könnt ihr dieses Klagen

(zumindest ab und zu)

auch sein lassen. Ich weiß, das ist nicht einfach zu akzeptieren, aber unter den gegebenen Umständen müsst ihr nunmal alternativlos bis zum Abitur durch die Schulmathematik durch

(und wenn sie noch so langweilig und unverständlich unterrichtet wird)!

Die Disziplin besteht hier also darin, sich zumindest zeitweise das Klagen zu verbieten - und viel zu üben.

(Vielleicht kommt der Appetit ja doch beim Essen, d.h., wenn man erste Erfolgserlebnisse hat;

und überhaupt ist es weitgehend unrealistisch zu hoffen, dass Lehrer einem den Spaß an ihrem Fach frei Haus mitliefern; nein, den Spaß muss man sich schon selbst erschaffen!

Und ich kann in meiner penetranten Altersweisheit Schülern nur raten, sich mindestens ein Schulfach vorzunehmen, in das sie freiwillig weit über das im Unterricht Geforderte hinaus "investieren" und sich eben den Spaß selbst erschafft

[genau so, wie man ein Hobby haben sollte, in dem man besser ist (oder überhaupt erst werden will) als alle Menschen im Umkreis von 100 m].)

Eigentlich hasse ich ja solche Spießerweisheiten, aber "es ist noch keinem was geschenkt worden"

(zumindest, wenn man nicht "von Geburt an" ein Mathe-Crack [s.o.] ist).

Ich bin da schizophren:

einerseits glaube ich, dass jeder Mathematik kann

(wenn er diszipliniert fleißig ist - und einen verständlichen und "ansteckenden" Matheunterricht erlebt);

andererseits kenne ich mindestens einen (erwachsenen) Menschen, bei dem mir sämtliche Voraussetzungen für Mathematik

(diszipliniertes mathematisches Denken)

zu fehlen scheinen.

Dabei verstehe ich unter "diszipliniertem mathematischem Denken"

Abstraktionsvermögen

(auch Abstraktion vom eigenen Standpunkt),

räumliche Vorstellung

(die sogar fürs Rechnen und keineswegs nur für die Geometrie wichtig ist),

mechanistisches Denken

(aus A folgt B folgt C: ),

hierarchisches Zergliedern eines Problems und Herausarbeiten von Strukturen.

Das Gegenteil von "diszipliniertem mathematischem Denken" könnte man vielleicht mit Claude Lévi-Strauss als "wildes Denken" bezeichnen

(das keineswegs auf Naturvölker beschränkt ist):

"Der Begriff wildes Denken (franz. pensée sauvage) wurde von dem Ethnologen Claude Lévi-Strauss geprägt. Er benannte damit die Denkweisen der naturnah lebenden Kulturen, die auf traditionell ganzheitlichen und mythisch erklärten Weltanschauungen beruhen. Alle Wesen, Dinge und Phänomene werden dabei durch einen allumfassenden, magischen Zusammenhang miteinander verbunden, der nicht auf abstrahierenden und rationalen Überlegungen beruht."
(Quelle: )

Ein ähnliches "anderes" Denken wird auch in Erich Fromms Buch

klar: es ist höchstens aus mathematischer Sicht ein unlogisches, chaotisches und wildes Denken, sondern funktioniert einfach nach einer anderen Logik

(assoziativ, nach Intensitäten geordnet ...).

Insbesondere gibt es viele Schüler, die noch sehr kindlich sind und in einer magischen Traumwelt leben - und denen somit mathematische Disziplin (vorerst) wesensfremd ist.

Sicherlich beherrschen alle (modernen) Menschen ansatzweise beide "Logiken", also sowohl die mathematische als auch die "wilde"

(wenn viele auch eine der beiden "Logiken" leugnen, was dann insgesamt zur rabiaten Trennung in die

führt).

Im Gegensatz zum "wilden" Denken ist das mathematische Denken oftmals ein sehr gezähmtes bzw. diszipliniertes Denken

(das nicht jedem "liegt", ja auf viele sogar abstoßend eiskalt wirkt, weil sie

[insbesondere im gängigen, schnarchlangweiligen Mathematikunterricht]

nie erlebt haben, dass es auch in der Mathematik "wilde", kreative Elemente gibt:

Eine gewisse Einseitigkeit ist aber wohl nicht zu vermeiden: wer sich wirklich für egal was (eben z.B. Mathematik) interessiert und dafür viel Zeit, Herzblut und Gehirnschmalz "investiert", wird das notgedrungen auf Kosten anderer Beschäftigungen und Interessen tun müssen

(vgl. "die Träne im Knopfloch" auf Abiturfeiern: welch erhebendes Gefühl, dass einem plötzlich 1000 [Berufs-]Türen offenstehen - und welche Tragik, dass man davon 999 zugunsten des einen, lebenslänglichen [!] Berufs sofort wieder zuschlagen muss; kein Wunder, dass viele Abiturienten nach dem Abitur erstmal ein "freies" Jahr einlegen

[und damit - hurra! - G8 ein Schnippchen schlagen]:

Zwar wehre ich mich gegen Klischees wie "Wahnsinn und Genie gehen Hand in Hand"

(die Rache der Dummen und allzu Normalen)

und dagegen, dass ausnahmslos alle (guten) Mathematiker Nerds sind

(vgl. nur das Klischee Sheldon in , einer sitcom, in der es ausschließlich und ad infinitum darum geht, ob emotional und sozial schwestbehinderte Nerds nicht eben doch ein [genauso klischeehaftes] blondes Dummchen ins Bett kriegen;

und damit's auch mächtig wissenschaftlich aussieht, hängen da immer ungemein ehrfurchtsgebietende physikalisch-mathematische Formeln rum: ).

Aber die Denkdisziplin in der Mathematik ist oftmals

(und zwar insbesondere bei zweitklassigen Mathematikern)

eben doch nur reine

(beim Zustand der [Innen-]Welt allemal verständliche)

Weltflucht

(die wahrhaft großen Mathematiker waren hingegen oftmals durchaus offen für andere, auch die Mathematik anregende Bereiche wie z.B. Philosophie oder Kunst).

Auch nur ein Klischee ist es, dass Mathematiker besonders intelligent sind. Wenn überhaupt, so sind sie oftmals nur einseitig intelligent, da es verschiedene Formen der Intelligenz gibt. Vgl. .

(Dass die meisten [guten] Mathematiker vermutlich einseitig intelligent sind, heißt nicht, dass sie als ausgleichende Gerechtigkeit anderweitig minderbemittelt sind: vermutlich sind sie ansonsten Durchschnitt, also wie du und ich.)

Gute Mathematiker haben wohl vor allem die mathematische Disziplin internalisiert.

Es gibt für Schüler zwei Arten mathematischer Erfolgserlebnisse:

einerseits äußere, "extrinsische" Erfolgserlebnisse: man erreicht gute Schulnoten in Mathematik und Anerkennung durch Lehrer, Eltern und Mitschüler

(vor allem viele junge Schüler arbeiten [wenn überhaupt] nur für diese äußeren Erfolgserlebnisse

[und unterwerfen sich dafür auch manchmal der mathematischen Disziplin];

was mich aber doch manchmal gewundert hat, sind ältere Schüler, die durchaus äußeren Erfolg u.a. in der Mathematik haben, aber nie über diese Orientierung an äußerem Erfolg

[der dann in einem guten Abitur und danach Karriere besteht]

hinaus kommen: also beispielsweise Abiturienten mit

[heutzutage keine Kunst mehr]

gutem Abitur, aber eingestandenermaßen noch immer

[und vielleicht lebenslänglich]

keinerlei "innerem" Interesse an irgendwas

[vgl. etwa ];

als ich mal zu einem Freund sagte, dass es mich wundere, wie einige Menschen für ihre Karriere alle ehemaligen Überzeugungen [und Interessen] verraten könnten

[und mich fragte, ob sie diesen Verrat noch bemerken würden],

gab der Freund eine Antwort, die mich wie ein Blitz getroffen hat: dass nämlich viele Menschen nie andere Ideale und Interessen als eben ihre Karriere hatten);

andererseits innere, "intrinsische" Erfolgserlebnisse: man hat mathematische Probleme erfolgreich "geknackt" - und "Blut geleckt".

Die Hoffnung eines jeden Lehrers ist wohl, dass zumindest einige Schüler von den äußeren zu den inneren Erfolgserlebnissen fortschreiten.

Manchmal frage ich mich, was eher ist:

das Ei, nämlich mathematische Disziplin, die zu Erfolgserlebnissen führt,
oder die Henne, nämlich mathematische Erfolgserlebnisse, die einem mathematische Disziplin überhaupt erst wünschenswert erscheinen lassen.

Und manchmal scheint mir, dass alles schon vorweg entschieden ist:

den einen Schülern "liegen" von Anfang an die Mathematik und deren Denkdisziplin (s.u.) - und entsprechend haben sie von Anfang an Erfolgserlebnisse,
die anderen Schüler kann man nur zu mathematischen Denkdisziplin anhalten

(sie ihnen wünschenswert erscheinen lassen)

und hoffen, dass sie dadurch irgendwann auch

(erst äußere, später vielleicht auch innere)

Erfolgserlebnisse haben.

Sicherlich gibt es Formen der Disziplin, die in allen (Schul-)Fächern wichtig sind, nämlich z.B.

(was auch nur Sekundärtugenden sind:)

Fleiß,
Durchhaltevermögen

(das [wie alles andere hier] sagt sich so leicht: da kann man sich den Mund fusselig reden),

dass man langfristig statt immer nur "auf den letzten Drücker" übt,
Konzentration

(also z.B. kein "multitasking": während man übt, hat der Computer ausgeschaltet zu sein und hört man auch keine Musik

[Ausnahmen bestätigen wie immer die Regel];

jede Wette, dass die Arbeitszimmer vieler "richtiger" Mathematiker - abgesehen von Mathematikbüchern - Mönchsklausen ähneln, und an der Tür jedes Arbeitszimmers sollte ein ähnliches Schild hängen wie

"In Erwägung, daß ich nur ein paar Wochen im Jahr für mich arbeiten kann;
in Erwägung, daß ich arbeitend auf meine Gesundheit achten muß;
in Erwägung, daß bei dem Schreiben von Stücken und dem Lesen von Kriminalromanen jede menschliche Stimme im Haus oder vor dem Haus eine willkommene Ausrede für eine Unterbrechung bildet,
habe ich beschlossen, mir eine Sphäre der Isolierung zu schaffen, und benutze dazu das Stockwerk mit meinem Arbeitszimmer und den kleinen Platz vor dem Haus, begrenzt durch Gewächshaus und Laube.
Ich bitte, diese Regelung nicht als allzu bindend aufzufassen. Prinzipien halten sich am Leben durch ihre Verletzung."
(Bert Brecht)

)

Aber es gibt auch Formen der Disziplin, die mir besonders in der Mathematik oder gar nur in ihr wichtig zu sein scheinen:

eine äußere Form der Disziplin, die auch in anderen Schulfächern wichtig sein mag, aber in der Mathematik besonders wichtig ist, scheint mir rigide zu sein

(die nicht für den Lehrer, sondern für einen selbst ist):

eine schöne oder zumindest für einen selbst klar erkennbare Schrift.

Ein Beispiel aus meiner eigenen Schulzeit: ich habe die Variable "icks" immer so und die Variable "ypsilon" immer so geschrieben. Dabei ist mir das "ypsilon" aber häufig so geraten, und dann habe ich es gerne - mit fatalen Folgen - mit dem verwechselt. Damit war's schnell vorbei, als ich das "ypsilon" systematisch in Schreibschrift, also so geschrieben habe.

Man mache lange Zeit

(bis man's aus dem FF beherrscht)

nicht mehrere Rechenschritte

(auch eine Form des Multitaskings)

auf einmal, sondern beschäftige sich immer nur mit einem Teil einer Rechnung - und schleppe den Rest erstmal unverändert

(und hübsch untereinander; s.u.)

mit.

Dadurch dauert eine Rechnung zwar länger, muss man mehr schreiben und braucht man auch mehr Papier

("spart Papier in Nebenfächern wie Deutsch oder Englisch oder in einer toten Sprache wie Französisch").

Dafür gibt es aber auch weniger Fehlerquellen.

Ein Musterbeispiel:

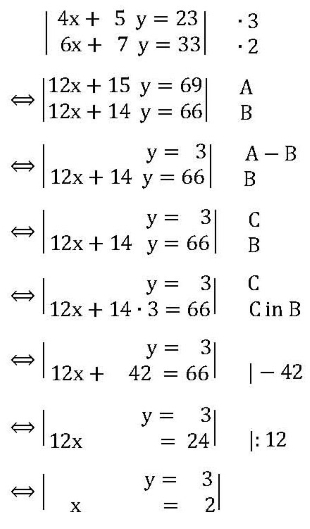
(... woran im Unterricht allerdings jedes Detail explizit durchgenommen werden muss;
also z.B., warum immer zwei [teilweise sogar unveränderte] Gleichungen mitgeschleppt werden;
oder was die Äquivalenzzeichen "sollen" und weshalb keines vor der ersten Zeile steht.)

Es scheint meine Erfindung zu sein: systematisches Untereinander-Rechnen, das einen stets Überblick behalten lässt:

Bild
(wobei mal dahingestellt sei, welchen Sinn solch eine Aufgabe haben mag)

Benutzung von Farbstiften:

z.B. wird alles in einer Aufgabe, was bekannt ist, grün unterstrichen, und alles, was unbekannt ist, rot;
oder farbliche Markierung aller mathematischen Informationen in einer Textaufgabe.

Schon mathe-typischer:

man halte sich in der Regel eisern an die festgelegten Schreibweisen. So werden z.B.

Dreiecksseiten mit den Kleinbuchstaben a, b und c bezeichnet

(und die Dreiecksseite, die in einem rechtwinkligen Dreieck gegenüber vom rechten Winkel liegt, also die "Hypotenuse", heißt immer c),

Dreieckseckpunkte hingegen mit den Großbuchstaben A, B und C.

Nur wenn man sich so pingelig an die Schreibweisen hält, kann man sich sehr leicht (und international) über Mathematik "unterhalten".

In der Mathematik gibt es

(abgesehen von Überschlagsrechnungen, die allerdings viel zu selten im Unterricht auftauchen)

kein "ungefähr", sondern nur ein "exakt"

(s.u. bei der Bestimmung des Schnittpunkts zweier Geraden).

Z.B. ist die Umformung

(nach der ersten binomischen Formel)

(a + b)² = a² + b²

nicht zu zwei Dritteln richtig, sondern zu 100 % falsch.

Richtig müsste es natürlich heißen: (a + b)² = a² + 2ab + b².

Solch gnadenlose Exaktheit unterscheidet die Mathematik wohl von den meisten anderen Fächern: wenn ich beispielsweise in einem englischen Satz ein einziges Wort falsch übersetze, bleibt der Rest dennoch richtig - und der Satz sogar oftmals verständlich.

Und doch wird mir die Exaktheit in der Schulmathematik oftmals zu hoch gehängt: es gibt Mathelehrer, die sich das Korrigieren einfach machen, indem sie überhaupt nur das Endergebnis bewerten: ist es falsch, gibt es keinen einzigen Punkt, selbst wenn

im Laufe der Rechnung nur ein einziger Rechenfehler gemacht wurde

(wodurch dann natürlich auch das Endergebnis falsch ist),

alles andere aber richtig war.

Man bedenke immer: auch viele große Mathematiker haben sich andauernd verrechnet - aber brillante Gedanken gehabt.

Die beiden letztgenannten Punkte

(also einheitliche Schreibweisen und absolute Exaktheit)

sorgen vielleicht am allermeisten dafür

(neben

dem oftmals vermittelten Eindruck, dass die Mathematik jedes Problem lösen kann,

sowie dem ebenso oftmals vermittelten Anspruch, dass auf die Dauer die gesamte Wirklichkeit mathematisiert werden kann - und dass unwichtig ist bis geradezu nicht existiert, was nicht mathematisierbar ist),

dass viele Menschen die Mathematik als besserwisserisch, gnadenlos und grundspießig empfinden.

Die eigentliche, nämlich innere mathematische Disziplin ist aber eine Denkdisziplin bzw. eine Herangehensweise, wie es sie in dieser Ridigität vielleicht nur in der Mathematik gibt.

Dafür nur ein einziges Beispiel aus einer 7. Klasse:

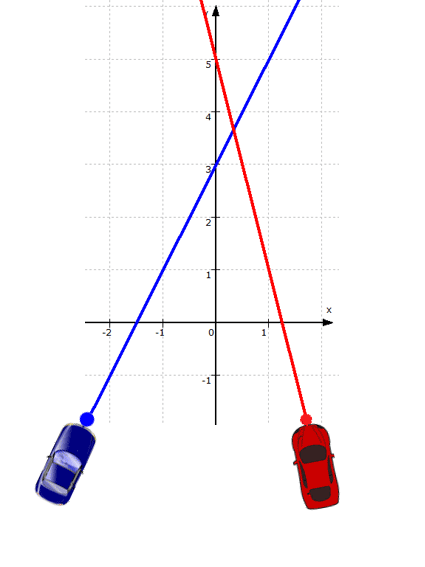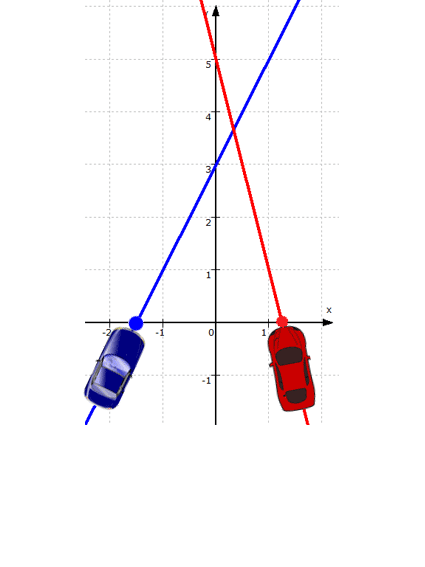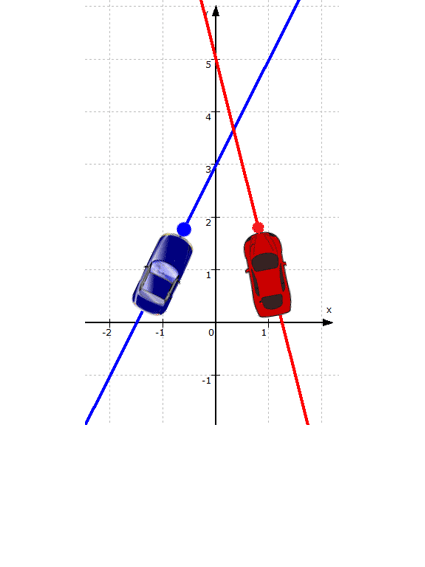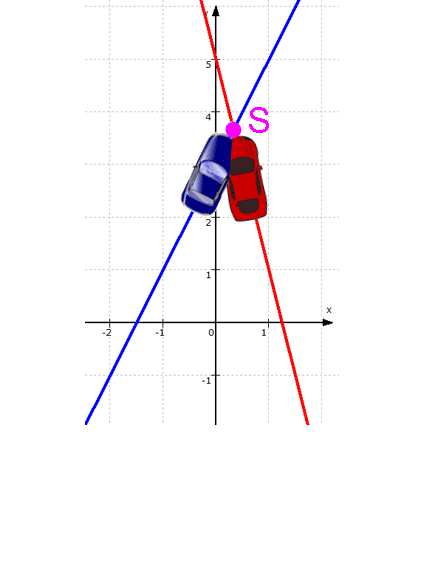
Gegeben seien zwei Geraden mit den Funktionsgleichungen f: y = 2x + 3 und g: y = - 4x + 5. Gesucht ist ihr Schnittpunkt S.

(Aber wen interessieren schon zwei Geraden und dann auch noch ihr Schnittpunkt?!

Nebenbei: um unangenehme Überraschungen zu vermeiden, kann es nicht schaden, sich schon vorweg klarzumachen, was "im Prinzip" rauskommen wird: da die beiden Geraden f und g unterschiedliche Steigungen haben, nämlich f die Steigung 2 und g die Steigung - 4, sind sie weder parallel noch identisch, sondern schneiden sie sich tatsächlich in einem Punkt S. Unklar ist bislang nur, wo dieser Schnittpunkt liegt.)

Zuerst die beiden Geraden im Koordinatensystem:

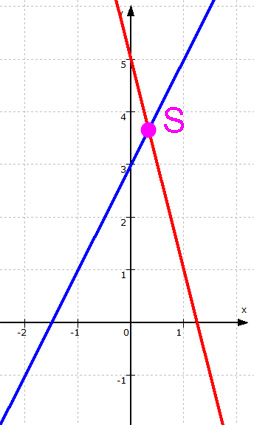
Mit diesem Bild ist eigentlich alles schon klar, denn man sieht den Schnittpunkt S ja direkt am Kreuzungspunkt der beiden Geraden.

Schwieriger wird's schon, wenn man wissen will, wo der Schnittpunkt S ( x | y ) liegt, d.h. welche Koordinaten x und y er denn hat.

(Aber wen interessieren schon die Koordinaten eines Schnittpunkts?!)

Nun kann man die beiden Koordinaten ablesen als

x ≈ 0,3
y ≈ 3,7

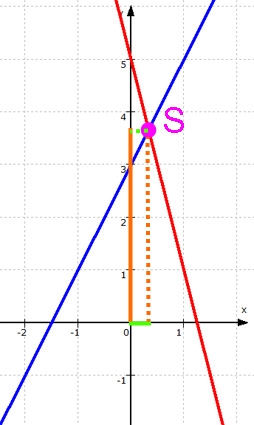
Weil die Skizze so klein ist, sind die gefundenen Werte für x und y aber vermutlich nur ungenau. Wie groß sind sie nun aber absolut genau ?

(Aber wer will's schon so genau wissen?!)

Um die Frage nach dem genauen Koordinaten x und y des Schnittpunkts S zu beantworten, zerlegen die Mathematiker die Aufgabe auf den ersten Blick höchst umständlich in zwei Teile

(Mathematiker sind oftmals zu blöd, um zwei Sachen auf einmal zu machen):

wenn S der Schnittpunkt der Geraden f und g ist,
muss S

auf f

UND

auf g

liegen.

Zu 1., dass S also auf der Geraden f liegt:

dazu vergessen wir für einige Zeit, dass S auch auf g liegt. Obige Zeichnung im Koordinatensystem vereinfacht sich also zu

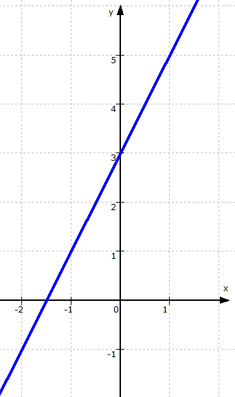Wenn aber S ( x | y ) auf f liegt,

müssen seine Koordinaten x und y die Funktionsgleichung y = 2x + 3 von f erfüllen,

muss also gelten:

y = 2x + 3

Das gilt wohlgemerkt für die Koordinaten aller Punkte auf der Geraden f, d.h. S ist bislang nur einer von unendlich vielen Punkten auf f :

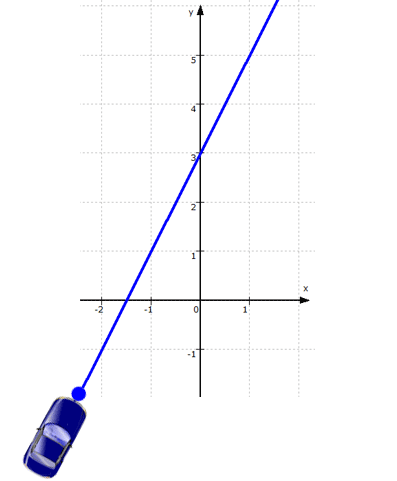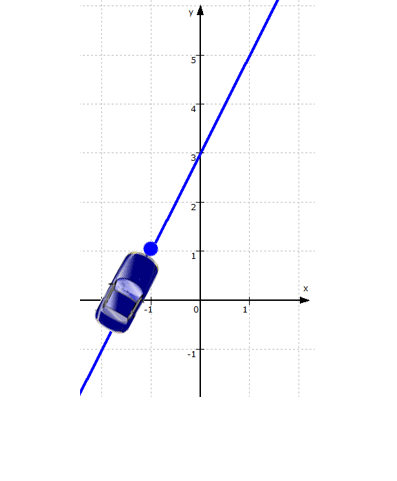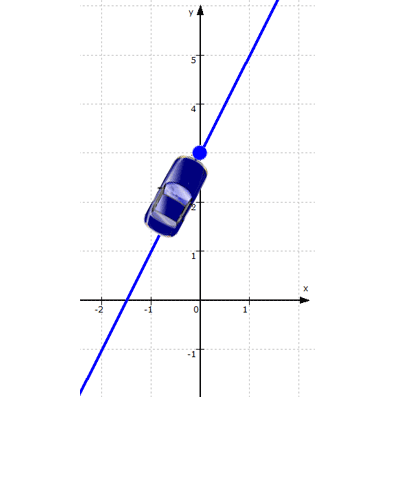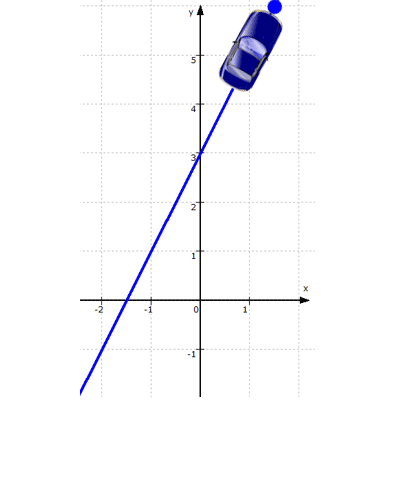
Wir wissen hier in 1. nur,

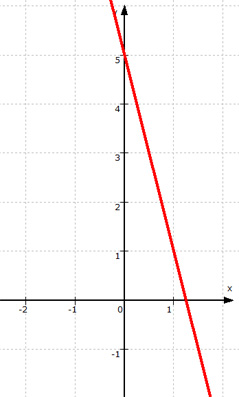
dass der Punkt S auf der Geraden f liegt, aber

noch nicht, wo er liegt.

Zu 2., dass S also auf der anderen Geraden g liegt:

dazu vergessen wir für einige Zeit, dass S auch auf f liegt. Es ergibt sich die vereinfachte Zeichnung

Wenn aber S ( x | y ) auf g liegt,

müssen seine Koordinaten x und y die Funktionsgleichung y = - 4x + 5 von g erfüllen,

muss also gelten:

y = - 4x + 5

Das gilt wohlgemerkt für die Koordinaten aller Punkte auf der Geraden g, d.h. S ist bislang nur einer von unendlich vielen Punkten auf g :

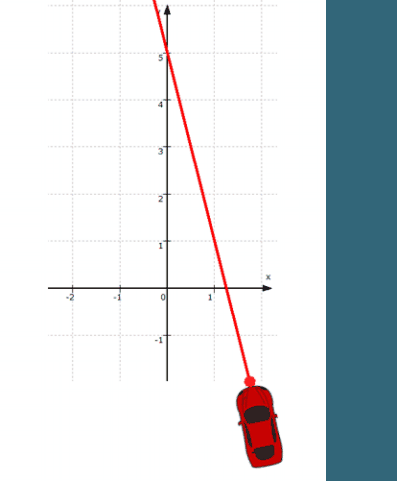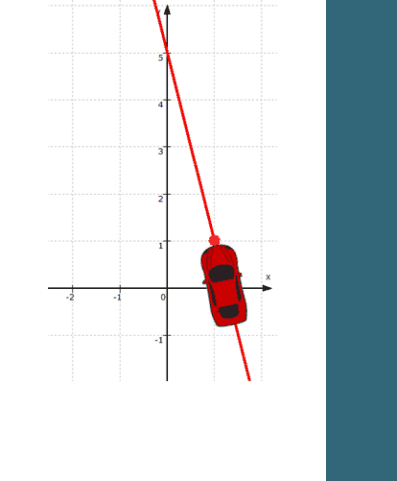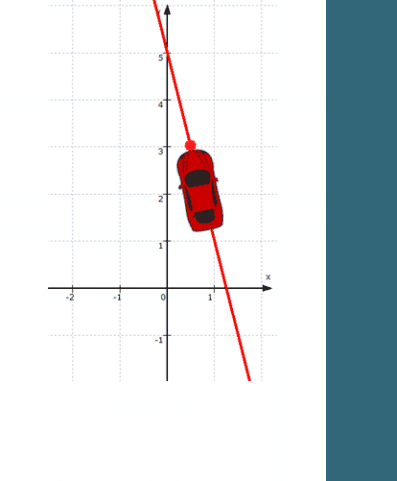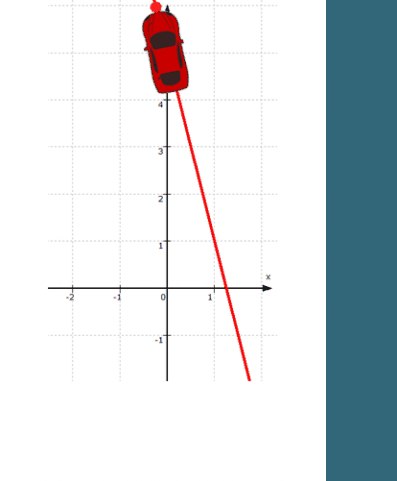
Wir wissen hier in 2. nur,

dass der Punkt S auf der Geraden g liegt, aber

noch nicht, wo er liegt.

Und jetzt setzen wir wieder zusammen, was wir in 1. und 2. noch getrennt betrachtet hatten:

als Schnittpunkt der Geraden f und g liegt S

auf f

UND

auf g,

was nach 1. und 2. bedeutet, dass für die Koordinaten x und y von S ( x | y ) gilt:

y = 2x + 3

UND

y = - 4x + 5

Das können wir auch in anderer Reihenfolge als sogenanntes "Enjambement" schreiben

(Enjambement heißt, dass ein Satzteil [in der folgenden Misereor-Werbung "2 Euro"] sowohl zum ersten als auch zum zweiten Satz gehört:

Nebenbei: es ist doch allemal interessant, dass das Enjambement hier als [mathematische] Schnittmenge zweier Sprechblasen dargestellt ist.)

oder kurz

Diese Gleichung hat gleichzeitig einen Nach- und einen Vorteil:

der Nachteil: das y, das wir ja auch ermitteln wollen, ist plötzlich futsch

(wir werden diesen Nachteil allerdings unten schnell beheben),

der Vorteil: wir haben nur noch eine einzige Gleichung mit der einzigen Unbekannten x, und das könnte lösbar sein

(genau genommen wissen wir sogar schon, dass es tatsächlich lösbar ist, denn wie wir bereits anfangs gesehen haben, müssen die beiden Geraden f und g einen Schnittpunkt S haben)

Jetzt aber erstmal eine Veranschaulichung:

Spätestens mit der Gleichung 2x + 3 = - 4x + 5 sind wir nun aber in der reinen Algebra und können wir für einige Zeit das Geradenproblem vergessen.

Es ergibt sich

2x + 3 = - 4x + 5 | + 4x

⇔ 6x + 3 = 5 | - 3

⇔ 6x = 2 | : 6

⇔ x =

Damit können wir schon wieder kurz aus der reinen Algebra auftauchen: mit x = kennen wir nunmehr immerhin schon die erste Koordinate des Schnittpunkts S und erhalten schon S ( | y ).

Glücklicherweise haben wir aber im Hinterkopf noch die beiden Gleichungen y = 2x + 3 und y = - 4x + 5, die Verbindungen zwischen y und x aufzeigen. Und eine von beiden Gleichungen reicht sogar. Nahmen wir die erste, also y = 2x + 3 . Wenn wir darin nun das inzwischen bekannte x = einsetzen, so erhalten wir

y = 2 x + 3

y = 2 • + 3 = 3 .

Damit haben wir nun

(obwohl uns y zwischenzeitlich kurz abhanden gekommen war)

auch die zweite Koordinate von S und erhalten insgesamt S ( | 3 ) bzw. mit Dezimalzahlen S ( 0,3 | 3,6 ).

Das sind jetzt - wohlgemerkt - exakte Ergebnisse. Weil sie aber periodisch sind, hätten wir sie niemals aus einer noch so genauen Zeichnung und mit noch so genauem Abmessen ablesen können.

(Zur Erinnerung: oben hatten wir nur die ungefähre Position S ( 0,3 | 3,7 ) des Schnittpunkts abgelesen.)

Zuguterletzt sei die typisch mathematische Denkweise auf den Punkt gebracht, die sich völlig vom alltäglichen Denken unterscheidet

(und eben das macht die mathematische Denkweise für viele so schwierig):

S ist der Schnittpunkt der beiden Geraden
f: y = 2x + 3 und g: y = - 4x + 5

S ( x \| y ) liegt auf f	S ( x \| y ) liegt auf g

die Koordinaten von S erfüllen die Funktionsgleichung von f	die Koordinaten von S erfüllen die Funktionsgleichung von g

y = 2x + 3	y = - 4x + 5

2x + 3 = - 4x + 5

x =

S (

| y )

entweder

oder xxxx

y = 2 • + 3	y = - 4 • + 5

y = 3	y = 3

S (

| 3

)

Die Denkstruktur sieht also insgesamt so aus:

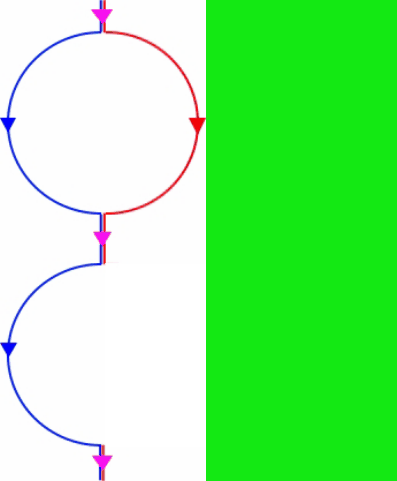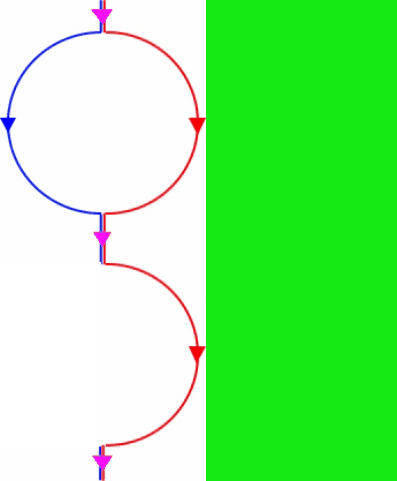
So schön (typisch mathematisch) symmetrisch diese Denkstruktur ist, so "abgenagt" ist sie doch auch - und für Laien

(z.B. mit der rabiaten Fallunterscheidung links / rechts)

völlig ungewöhnlich

(Viele haben schon Schwierigkeiten mit der Logik der keineswegs benutzerfreundlichen Bahn-Fahrkartenautomaten .)

Natürlich denkt kein richtiger Mathematiker mehr so umständlich, sondern bei ihm ist es zum Automatismus geworden:

Schnittpunkt zweier Geraden? → Geradenterme gleichsetzen!

Man kann das auch im Schulunterricht so halten, d.h. nur das simple Gleichsetzungsverfahren "beibringen". Dann aber werden Schüler nur rechnen, aber nicht die zentralen Grundlagen verstehen, nämlich z.B.

ein Punkt S ( x | y ) liegt genau dann auf einem Funktionsgraphen,
wenn seine beiden Koordinaten x und y die Funktionsgleichung erfüllen.