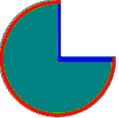"drei Viertel", "3 von 4", "3 durch 4" und last but not least "75 %"

Die Bruchrechnung ist doch zumindest rechnerisch äußerst simpel, wenn man sich

1. die wenigen Rechenregeln für

• die Bruchaddition,

• die Bruchsubtraktion,

• die Bruchmultiplikation,

• die Bruchdivision

(als Multiplikation mit dem Kehrwert des zweiten Bruchs),

2. die Regeln fürs Erweitern und Kürzen (von Zähler und Nenner gleichzeitig!) einbläut

(inkl. "Kürzen aus Summen / tun nur die Dummen")

und

3. bemerkt, dass all diese Regeln einzig und allein dazu dienen,

das Rechnen mit Brüchen auf das Rechnen mit (beim vorletzten Bruch jeweils im Zähler bzw. Nenner) ganzen Zahlen zu reduzieren: = Nicht nur Laien, sondern auch MathematikerInnen sind strubbeldumm: sie können überhaupt nicht mit Brüchen, sondern eben nur mit den simpelsten, also ganzen Zahlen rechnen.

Woher - wenn's rechnerisch so simpel ist - rühren dann denn überhaupt die leidigen Probleme mit der Bruchrechnung?

Es mangelt oftmals (vor und neben jeder Rechnung) vor allem an jeglicher Anschauung, und dieses Problem zeigt sich auch sprachlich:

Wie bereits gesagt, hängen dabei einerseits Sprache und andererseits Anschauung  direkt zusammen:

1. "drei Viertel":
   
    

1. Ein (!) Kuchen wird geviertelt, drei von diesen Vierteln werden zusammengezählt. *

oder

2. Arno isst drei Viertel eines (!) Kuchens. *
    

2. "3 von 4":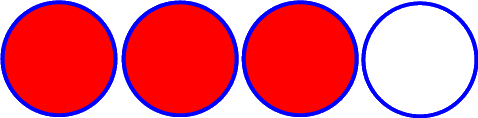    
   
   Man nimmt drei von vier Kuchen. *
    

3. "3 durch 4":
   
   Drei Kuchen werden an vier Leute (Arno, Berta, Caesar und Dagobert) verteilt *

(z.B.: Arno erhält bei der Verteilung von drei Kuchen an vier Leute den grünen Anteil * )

... und schon sind wir beim nächsten sprachlichen Problem:

                            "3                [geteilt] durch 4"

ist verwirrenderweise synonym mit

                                     "drei Kuchen werden an [!] vier Leute ver[!]teilt".

(Nebenbei: wenn vier Leute drei Kuchen essen, werden sie diese üblicherweise nicht in der Aufteilung

essen, sondern sich erst gemeinsam über den ersten, dann über den zweiten und zuguterletzt - wenn ihr Hunger noch immer nicht gestillt ist - über den dritten Kuchen hermachen. Die Aufteilung

ist also sehr abstrakt z.B. unter der Anweisung, drei Kuchen mit möglichst wenig Schnitten an vier Leute aufzuteilen.)

In 1. bis 3. wird schon überdeutlich, dass jeweils völlig unterschiedliche Sachverhalte gemeint sind - oder zumindest gemeint zu sein scheinen.

Vollends unübersichtlich wird's aber durch

4. "75 %", was ja nun in keinerlei Bezug mehr zum Vorherigen zu stehen scheint, da nicht mal mehr die 3 und die 4 auftauchen.

Dennoch ist "75 %" auch nur

• eine andere Schreibweise für einen Bruch

• bzw. auch nur ein Bruch:

75 % = 75 Prozent = 75 pro centum = 75 von hundert = 

Mehr noch: sind dasselbe (nur in anderer Schreibweise) wie , denn man kann aus durch Erweitern mit 25 erhalten:

=

Nun verbinde aber zumindest ich mit Prozenten nie - wie oben - eine runde Skala (Kreise), sondern eine lineare, und somit ist mein Bild von 75 %

Alle Klarheiten beseitigt?!

(Aber keine Bange, es kommt noch viel schlimmer :-)

Die Sprache

"drei Viertel", "3 von 4", "3 durch 4" und last but not least "75 %"

kodiert bzw. suggeriert also

(wenn man davon absieht, dass in 1. bis 3. immerhin noch jeweils die 3 und die 4 vorkommt)

vier völlig unterschiedliche Bilder

(und Handlungen bzw. Sachverhalte!; s.o. *).

Um ein wenig Klarheit zu erreichen, kann man sich nun fragen:

Wo bleiben die 3 und die 4 ? Oder genauer: wie kommen die jeweiligen Ergebnisse

(die ja normalerweise nicht vorgegeben sind, sondern erst konstruiert werden)

mittels 3 und 4 zustande?

Das missing link, das alle Ausdrucksweisen und Bilder zusammenführt (und mitverbindet), ist ziemlich abstrakt:

1. In

"drei Viertel":

• ist die GESAMTMEngE ein Vollkreis , aus dem durch Teilung in vier gleichgroße Teile

• als EINHEIT ein Viertelkreis, also entsteht.

Drei dieser EINHEITEN werden zur roten Fläche zusammengefasst.

2. In

"3 von 4":    

• besteht die GESAMTMEngE aus den vier Vollkreisen

,

woraus durch Teilung in vier gleichgroße Teile

• als EINHEIT ein Vollkreis, also entsteht.

Drei dieser EINHEITEN werden zur roten Gesamtfläche

 zusammengefasst.

(3. wird aus gutem Grund noch zurückgestellt; s.u.)

4. In

"75 %":

• ist

die GESAMTMEngE, aus der durch Teilung in vier gleichgroße Teile

• als EINHEIT entsteht.

Drei dieser EINHEITEN werden zur roten Gesamtfläche

zusammengefasst.

Damit aber zum ein wenig anders gelagerten Fall

"3 durch 4":
 

Hier

• besteht die GESAMTMEngE aus den drei Vollkreisen

,

aus denen durch Teilung in vier gleichgroße Teile

• als EINHEIT ein ³/₄-Kreis, also entsteht.

Von diesen EINHEITEN werden in diesem 3. Fall aber nicht mehr drei zusammengefasst

(also z.B.  ),

sondern die EINHEIT 1, EINHEIT 2, EINHEIT 3 und EINHEIT 4 bleiben vollständig nebeneinander stehen:

 

Nur in diesem 3. Fall liegt also eine eigentliche Teilung 3 : 4 bzw. vor.

Eigentlich sollte man also sprachlich und in der Schreibweise unterscheiden:

• "3 durch 4" bzw. 3 : 4 bzw. bedeutet etwas ganz anderes als
• drei Viertel bzw. ³/₄ .

Ich treibe hier die (unnötige?) Verkomplizierung bewusst auf die Spitze, um zu zeigen, dass die Bruchrechnung (u.a. für SchülerInnen) keineswegs so einfach ist, wie meist unterstellt wird.

Und schon sind wir beim nächsten sprachlichen Problem: "wovon" wird nämlich in der Mathematik verwirrenderweise durch ein "mal" ausgedrückt.

1. "drei Viertel":

   • 1= ³/₄

2. "3 von 4":    

   • 4 = 3

3. "75 %":

   • 100 = 75

Es kommt sprachlich sogar noch doller:

•  während eben noch gesagt worden war, dass "[wo]von" in der Mathematik üblicherweise durch ein "mal" (!) ausgedrückt wird,

• hatten wir oben 75 % mit 75 von (!) hundert =  gleichgesetzt, war da also mit dem "von" ein "durch" (!) gemeint.

Und um die Verwirrung vollständig zu machen, bedeutet "3 von [!] 4" (s.o.) nochmals was ganz Anderes.

Nach all der (übertriebenen?) Verkomplizierung erhalten wir aber ganz einfache Ergebnisse, wenn wir in 1., 2. und 4. als GESAMTMEngE einen (immer denselben!) Vollkreis wählen. In allen drei Fällen erhalten wir

• nach Vierteilung die EINHEIT

• und nach Verdreifachung das Ergebnis , d.h.

• die EINHEIT 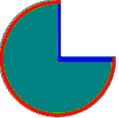in 3.

Und zuguterletzt lässt sich da auch noch 3. integrieren, wenn wir unter "3 durch 4"

• nicht verstehen, was jeweils Arno, Berta, Caesar und Dagobert bekommen

  ,

• sondern

(weil bei gerechtem Teilen bzw. genauer Viertelung ja alle einen gleichgroßen Anteil bekommen)

nur das, was ein Repräsentant, also z.B. Arno, bekommt: