Natürlich kann man das auch so machen:

  "Bestimme die Ortslinie aller Minima der Funktionenschar fa(x) = x2 - ax."

Die Rechnungen:

fa'(x) = 2x - a = 0

          x     =

(Die zweite Ableitung als Bestätigung dafür, dass da Minima vorliegen, sparen wir uns hier mal.)

y = ()2 - a•=- = -

Also ist y = - x2, und der Graph dieser Funktion ist die gesuchte Ortslinie der Minima.

Ich habe mir dabei sämtliche Erklärungen und Zwischenschritte gespart, damit um so deutlicher wird:

So kurz, so (hübsch) abstrakt!

Denn schauen wir uns doch mal an, was da passiert ist:

  • mittels der wenigen (und zudem endlich vielen) Rechenschritte

fa'(x) = 2x - a = 0   x = , y = ... = -, y = - x2

  • haben wir die Ortslinie gefunden, auf der die Minima sämtlicher (unendlich vieler!) einschlägiger Funktionen liegen.

Genau das aber, nämlich paradoxerweise

zu finden, kann nur die Mathematik bzw. ist ihre eigentliche Stärke/"Aufgabe".

Die extrem kurze Rechnung

fa'(x) = 2x - a = 0   x = , y = ... = -, y = - x2

hat also durchaus ihren ganz eigenen Reiz!

Ebenfalls als Vorteil und weiterer Reiz angesehen sei hier (erstmal), dass man für die Rechnung

fa'(x) = 2x - a = 0   x = , y = ... = -, y = - x2

(das könnte auch ein entsprechend programmierter Computer),

(genauer: den Graphen dieser Funktion)

haben muss:

es gibt gewisse simple Rechenmechanismen, die schnell und zuverlässig helfen, selbst wenn man nicht nicht die mindesten Vorstellung von einem Sachverhalt hat.

Und doch: was entgeht einem doch alles, wenn man derart ohne jede Vorstellung rechnet?!:

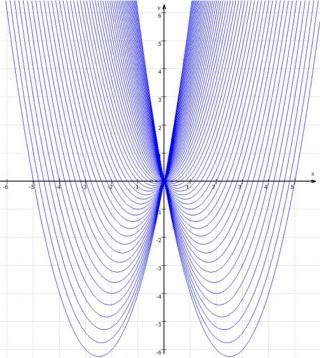
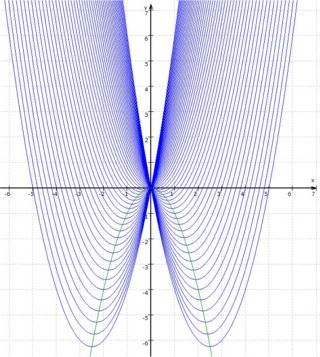
Solch anschauliches Vorgehen sollte zumindest am Anfang des schulischen Umgangs mit Funktionenscharen stehen. Die vollständige Abstraktion kann (sollte) dann später noch immer folgen - und hat dann ihren eigenen Wert.

Nebenbei: manchmal wird von "Funktionenschar", also im Plural, manchmal hingegen von "Funktionsschar", also im Singular, gesprochen, und beides scheint mir interessante unterschiedliche Perspektiven auf denselben Sachverhalt anzudeuten:

(und dementsprechend liegen alle Minima auf der Ortslinie),

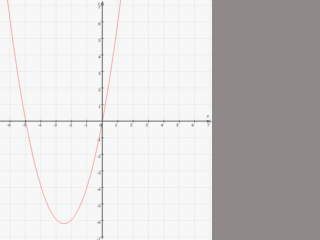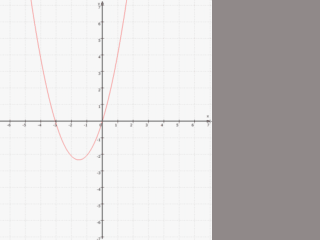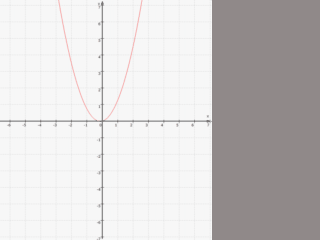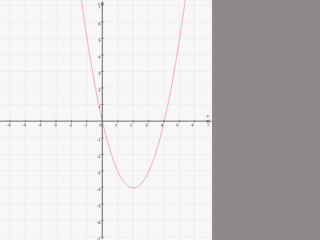
(und dementsprechend bewegt sich das [einzige] Minimum auf der Ortslinie). 

Mit "Orstlinien" sind wir aber schon ziemlich weit in den Bereich der "Funktionenscharen" eingedrungen.

Mir geht es hier aber um den allerersten Einstieg in Funktionenscharen.

Schauen wir uns dazu erstmal an, wozu man (?) Funktionenscharen überhaupt "braucht":

  1. Echte (außermathematische) Anwendungen sind mir unbekannt.
  2. Funktionenscharen werden gerne im Abitur herangezogen, um das Abstraktionsvermögen von SchülerInneN und damit ihre "sehr gut"-Würdigkeit abzuprüfen

(fragt sich nur, was an der Beherrschung von Funktionenscharen "sehr gut"-würdig ist, wenn sie nach einem eingepaukten Mechanismus funktioniert).

  1. - und das ist dann offensichtlich für mich die einzige Legitimation -, Funktionenscharen haben ihre ästhetischen Reize

(und wozu "braucht" man schon Ästhetik?!).

Warum sich also nicht

  1. vorgegebene Funktionenscharen auf ihre ästhetischen Reize hin untersuchen

(wobei man eine Menge über die mathematischen Eigenschaften erfahren kann!)

  1. und später auch ästhetisch schöne Funktionenscharen selbst herstellen?

Eine Kombination von A. und B. ist folgende Nach-Konstruktion (Simulation) einer vorgegebenen Funktionenschar.

Dabei ist das Nach-Konstruieren geradezu eine Chance: wenn die Funktionsweise des "Originals" (seine mathematischen Gleichungen) völlig bekannt wäre,  wäre doch eben auch schon alles verraten bzw. allzu suggestiv.

Ich habe über die Programmsammlung weder Negatives noch

(da ich leider nicht großzügig von der Firma bezahlt werde)

Positives zu sagen, außer dass ich den Namen "Nero" bei einem Brenn(!)programm für hübschen schwarzen Humor halte.

Wenn man eins der Sub-Programme der derzeit neuesten Version 9 öffnet, erscheint für einige Sekunden folgender "splash screen" (leider keine bessere Qualität möglich):

Und das ist doch - wie eine Schülerin sagte - " " . Dieser Schönheit lässt sich nun sukzessive nachgehen:

  1. sagte eine andere Schülerin, dass sie da ein dreidimensionales Band sehe,
  2. ergänzte ein anderer Schüler, das Band "wehe" und "fließe".
  3. ergänzte wieder ein anderer, die Einzelgraphen seien annähernd Sinusgraphen 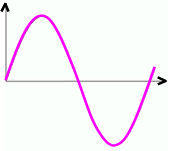, und deren Schönheit lässt sich schon genauer beschreiben: sie sind
    1. "stetig", d.h. mit einem einzigen durchgezogenen Strich ohne Absetzen zeichenbar,
    2. hübsch geschwungen ("differenzierbar") statt mit Knicken

("Die lateinische Bezeichnung „Sinus“ 'Bogen, Krümmung, Busen' für diesen mathematischen Begriff wählte Gerhard von Cremona 1175 [...]"
[Quelle: ]) 

  1. verlässlich periodisch,
  2. nach oben und unten beschränkt, also auch in diesem Sinne schön übersichtlich.

Erster Schritt ist also die Funktionsgleichung y = sin (x) mit dem Funktionsgraphen

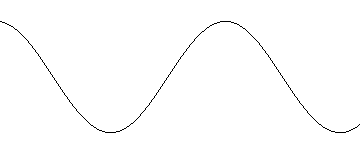
Hier halten wir aber bereits inne und stellen erstmal einige geradezu allgemeinbildende Überlegungen zum grundsätzlichen Umgang mit (egal welchen) Funktionsgraphen an:

wenn eine Funktion die Funktionsgleichung                 y =        Funktionsterm (      x      ) hat

(z.B. y = x2 oder y = oder eben y = sin (x) ),

so ergibt sich

  1. eine horizontale Verschiebung             ↔  durch  y =        Funktionsterm (     x + a)        ,
  2. eine vertikale Verschiebung                  ↕    durch  y =       Funktionsterm (     x      ) + b  ,
  3. eine horizontale Streckung/Stauchung ↔  durch  y =        Funktionsterm (c • x      )  ,
  4. eine vertikale Streckung/Stauchung      ↕    durch  y = d • Funktionsterm (      x      ) 
  5. ... und entsprechende Kombinationen beispielsweise für eine Verschiebung gleichzeitig nach links und nach oben.

Nun wollen wir als Erstes den Einzelgraph ans Laufen bekommen (horizontale Verschiebung) , was wir mit a., also y = Funktionsterm (x + a) , erreichen:

y = sin (x + a)

Der entsprechende Graph ist:

Wohlgemerkt: nur zur Darstellung des bewegten Einzelgraphen brauchen wir bereits eine ganze Funktionenschar!

Des Weiteren soll der Einzelgraph vertikal gestaucht und gestreckt werden, was mittels  d., also y = d • Funktionsterm (x), möglich ist. Das Problem dabei ist, dass der Einzelgraph abwechselnd gestreckt und wieder gestaucht werden soll, was wir erreichen, indem wir für d nochmals einen Sinus einsetzen:

y = sin(a) • Funktionsterm (x + a)

Der zugehörige Einzelgraph sieht damit inzwischen so aus:

 

(Hier kommt zusätzlich zur Bewegung noch eine scheinbare Dreidimensionalität hinzu, die an erinnert; vgl. Bild.) 

Nun wollen wir mehrere solche Graphen untereinander haben, was wir mittels  b., also y =       Funktionsterm ( x ) + b , erreichen:

y = sin(a) • Funktionsterm (x + a) + b 

Wenn man aber bei noch genauer hinschaut, so erkennt man, dass die verschiedenen Einzelgraphen nicht nur untereinander, sondern auch noch leicht seitlich zueinander versetzt liegen:

 

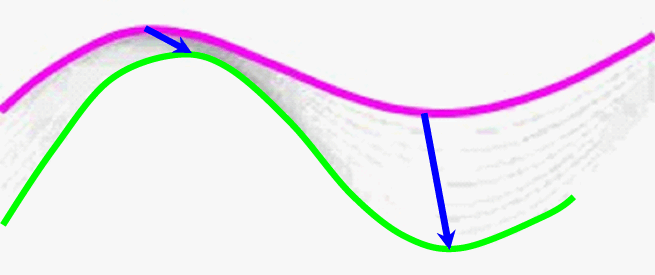
Das erreichen wir nochmals mit a., also y = Funktionsterm (x + a):

y = sin(a) • Funktionsterm (x + a + e) + b 

Wohlgemerkt: wir haben damit

Damit sieht unsere endgültige Simulation so aus: 

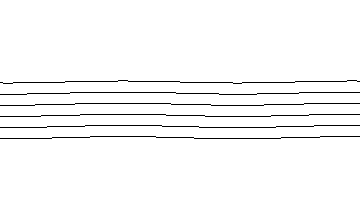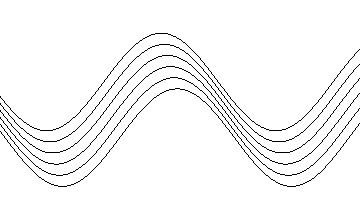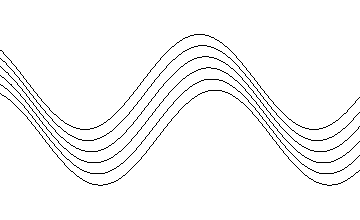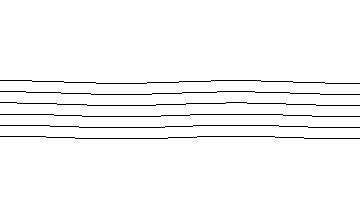
Download der -Datei:
(Download des benötigten Freeware-Programms : )

Es ist mir bislang nicht gelungen, mit der Firma Nero Kontakt aufzunehmen und von ihr ein besseres Video des "splash screens" oder gar die mathematischen Gleichungen für ihn zu bekommen. Und das ist auch gut so, denn die fertigen Gleichungen wären vermutlich doch allzu suggestiv, und sowieso macht es mehr Spaß, mit einigem Stolz selbst "drauf" zu kommen. 0

Keine Ahnung, was man von all dem hat, und wirklich anschaulich verstehe ich die Zusammenhänge noch immer nicht. Und überhaupt: wie wussten das Volumen, die Flächen und der Umfang, dass sie derart (über die Ableitung) zusammenhängen sollten?

Überhaupt scheinen derzeit (2008/9) Funktionenscharen schwer en vogue zu sein:

- wobei doch allemal bemerkenswert ist, dass die rechte Schar wie ein fliegender Vogel (oder ein aufgeschlagenes Buch?) aussieht.

Und siehe auch den Vista-Boot-Bildschirm

Usw. usf.:


(hier sogar eine 3D-Funktionenschar)

Aber auch anderweitig sind Funktionenscharen gerade "in":



(IPhone)



(Samsung Pixon 12; vgl. )

(Es gibt in Werbung und Design ganz wenige Kreative,
und der Rest [die Creativen] tritt dann nur jeden Trend endlos breit.)

Vermutlich tauchen Funktionenscharen so oft auf, weil sie "Dynamik" suggerieren,
und zwar insbesondere, wenn sie in Bewegung auftauchen.

Vgl. auch Disco-Lasershows à la

PS:


(man beachte die Schwaden über dem Kaffee!)