vier typische "Anwendungen" der Ableitung / Integration

Im Folgenden geht es

(anhand von drei "Groß"-Aufgaben)

um vier Aufgabentypen, die fast das gesamte Spektrum der Analysis (Ableitung, Integration) im Abitur abdecken dürften.

Alle vier Aufgabe sind sowas von (verlässlichem) Standard, dass sie Lehrern sehr einfach erscheinen mögen. Das kann aber nur sagen, wer solche Aufgaben vorher schon mal gesehen hat.

Bei der „Ergründung“ der Aufgaben geht es mir nicht um die konkreten

(eines Mathematikers unwürdigen)

Rechnungen, sondern um zweierlei:

1. darum, wie man die Aufgaben „knackt“, also die Mathematik in ihnen wiederentdeckt, die die Aufgaben-Autoren mehr oder weniger gut in den Aufgabentexten versteckt haben;

2. um die zentralen Lösungsschritte, die dann nur noch mit konkreten Rechnungen gefüllt werden müssten.

(Um die „strukturellen“ Fähigkeiten der Schüler zu trainieren, habe ich mit ihnen an Aufgaben oftmals nur diese zentralen Lösungsschritte erarbeitet - und sie ermutigt, in Klassenarbeiten zumindest diese aufzuschreiben und dann dafür viele [!] Punkte zu bekommen, selbst wenn sie die Rechnungen nicht [richtig] schafften oder unter Zeitdruck nicht dazu kamen

... also etwa so wie in mündlichen Abiturprüfungen, in denen keine Zeit für umständliche Rechnungen ist.)

Bei den im Folgenden behandelten außermathematischen Anwendungsaufgaben 1. und 3. (und damit 4.) wird nicht gefragt,

• ob die Anwendungen realistisch geschweige denn für Schüler lebensnah sind

(und schon gar nicht, ob letzteres überhaupt ein Kriterium sein kann / sollte),

• und auch nicht, ob sie innerhalb der Schulmathematik sinnvoll sind.

Vorweg etwas "Lebenswichtiges", das vielen Schülern aber unbekannt zu sein scheint:

ein Punkt P (x | y ) liegt genau dann auf dem Graphen einer Funktion f,

 (Vgl. oder .)

Das ist eigentlich banal, weil Funktionsgraphen ja überhaupt erst so zustande kommen.

Ein Beispiel:

P ( 3 | 9 ) liegt auf dem Graphen der Funktion f: y = x²,

Einschub für Lehrer: warum aber kennen meiner Erfahrung nach viele Schüler diese Banalität nicht [wenn man diese Unkenntnis nicht (allzu) einfach damit erklären will, dass „die Jugend von heute“ (wie schon spätestens seit Platon bekannt) notorisch faul & dumm ist]? Und überhaupt: war das nur bei meinen Schülern so, also mein Fehler? So oder so scheint mir, dass allzu leicht die nur anfänglich gezeigte Entstehung von Funktionsgraphen hinter der massenhaften späteren Verwendung fertiger Funktionsgraphen verschwindet (... eine Gefahr, die wohl noch dadurch erhöht wird, dass heutzutage Computer und GTR (= grafikfähige Taschenrechner) allzu leicht fertige Funktionsgraphen anzeigen; nebenbei: mit Freude und später Genugtuung habe ich jetzt Folgendes gelesen: „In Baden-Württemberg ist der Einsatz von Grafikrechnern ab dem Abitur 2017 (berufliche Gymnasien) bzw. 2019 (allgemeinbildende Gymnasien) verboten.“ [Quelle: ] Ist es nicht herrlich, wie Kultusministerien andauernd das verbieten, was sie eben noch vorgeschrieben haben - und umgekehrt?!)

1.

„Der Querschnitt eines Gewächshauses kann durch die Funktion f mit f(x) = und die x-Achse beschrieben werden (x und f(x) in m). Wegen der geforderten guten Belüftung soll ein rechteckiges Tor so eingebaut werden (s. Figur 1), dass dessen Fläche möglichst groß ist. Berechnen Sie die Maße des Tores und seinen maximalen Flächeninhalt.“ [die Quelle ist mir leider unbekannt, weil die Aufgabe auf einem abgeschnittenen Zettel stand]   Figur 1 mit Beispieltor

Angenommen mal, Figur 1 wäre nicht mitgeliefert worden. Dann gälte es doch zu allererst, eine Vorstellung von der Form des Gewächshauses bzw. dem Graphen der Funktion f: y = - x² + 4 zu bekommen. Dazu gibt es drei Möglichkeiten:

1. : man lässt sich den Graphen von einem Computer bzw. grafischen Taschenrechner anzeigen;
2. : man bestimmt (hier ziemlich einfach) rechnerisch die Schnittpunkte des Funktionsgraphen mit der x-Achse (Nullstellen) und den Schnittpunkt mit der y-Achse;

2. ... oder wir verstehen die Funktionsgleichung f(x) = - x² + 4 :

   • wegen x² ist der Funktionsgraph parabelförmig:

• wegen ist der Funktionsgraph stark gestaucht:

• wegen - ist der Funktionsgraph nach unten geöffnet bzw. an der x-Achse gespiegelt:

• wegen + 4 ist der gesamte Funktionsgraph um 4 nach oben verschoben und sieht er insgesamt so aus: 

Das sind bislang alles nur ungenaue Planskizzen mit einer einzigen Gewissheit: der Funktionsgraph schneidet die y-Achse im Punkt S_y ( 0 | 4 ), d.h. das Gewächshaus ist 4 m hoch

(... eine Information, die wir im Folgenden aber gar nicht benötigen).

Insgesamt sieht das Gewächshaus also

• nicht, wie in den allermeisten Fällen, so eckig aus ,
• sondern eher so rundlich , nur dass es viel breiter ist:

Im Folgenden arbeiten wir aber mit dem Funktionsgraphen, den der Aufgaben-Autor freundlicherweise mitgeliefert hat:

Kommen wir damit zu dem Satz

„Wegen der geforderten guten Belüftung soll ein rechteckiges Tor so eingebaut werden (s. Figur 1), dass dessen Flächeninhalt möglichst groß ist“.

Das Tor soll laut Aufgabenstellung zwar einen möglichst großen Flächeninhalt haben, darf aber natürlich nicht größer als die Vorderfront des Gewächshauses sein. Anders gesagt: es ist in zweierlei Hinsicht begrenzt:

1. durch den Boden bzw. die  x-Achse,
2. durch die oberen Eckpunkte, die auf der Dachkante  bzw. dem Funktionsgraphen liegen.

(Nebenbei: beides wird auch schön anhand der Tür in deutlich.)

Nun ist in ausdrücklich nur ein Beispieltor eingezeichnet, das nicht automatisch die gesuchte größtmögliche Fläche hat.

Machen wir uns deshalb mal an einigen weiteren Beispielen klar, wie verschiedene mögliche Tore unter den Bedingungen a. und b. aussehen

(solche Überlegungen schreibt man natürlich nicht in einer Klassenarbeit / Klausur auf, aber es kann nicht schaden, sie entweder im Kopf durchzuspielen oder auf kurz auf einem Schmierzettel zu notieren):

Hier kann man schön sehen:

• je schmaler das Tor wird,
• desto höher wird es.

Und wenn wir den Film umgekehrt laufen lassen, also so

,

so sieht man:

• je breiter das Tor wird,
• desto flacher ist es.

Die Bedingung, dass die oberen Eckpunkte auf dem Funktionsgraphen liegen, zwingt Breite und Höhe also in einen Zusammenhang

(den wir allerdings noch genauer bestimmen müssen).

Man kann noch anderes entdecken:

• zunehmende Breite und dadurch abnehmende Höhe oder umgekehrt abnehmende Breite und dadurch zunehmende Höhe gleichen sich aber keineswegs gegenseitig aus

(wenn das der Fall wäre, wäre die Aufgabe, ein [!] größtes Tor zu finden, unsinnig),

d.h. der Zusammenhang von Breite und Höhe führt nicht dazu, dass alle möglichen Tore denselben Flächeninhalt haben, sondern z.B. ist der Flächeninhalt von

offensichtlich erheblich größer als der von

• Interessant sind insbesondere die Extremfälle:

  • wenn die Breite sehr groß wird, also z.B. bei

,

wird der Flächeninhalt sehr klein (mathematisch gesagt: geht er gegen null);

• wenn die Breite sehr klein wird, also z.B. bei

,

wird der Flächeninhalt ebenfalls sehr klein (wieder mathematisch gesagt: geht er gegen null).

Daraus folgt: da man die Breite kontinuierlich (stetig) verändern kann, muss irgendwo zwischen den Extremen „sehr breit / sehr schmal“ ein Rechteck mit größtem Flächeninhalt existieren

(oder mehrere Rechtecke, die alle denselben maximalen Flächeninhalt haben?).

• Von den oben gezeigten Rechtecken könnte

das mit dem größten Flächeninhalt sein.

10 und 3 sind aber nur ungefähre Schätzwerte, die wir jedoch später mit unseren rechnerischen Ergebnissen vergleichen können. Und falls diese Ergebnisse weit von unserem Schätzwert abweichen sollten, gibt es zwei Möglichkeiten:

• wir haben falsch geschätzt (warum?),

• wir haben uns verrechnet (warum?).

Nebenbei: man könnte all diese Überlegungen auch schön anschaulich an den Streifen von  aufhängen:

.

Von den gezeigten Rechtecken/Toren/Türen ist vermutlich das mit der größten Fläche, ermöglicht es also die beste Belüftung.

(Nur sieht man hier auch die Grenzen des mathematischen Modells: durch könnte ein Mensch wohl nur gebeugt gehen, und deshalb ist wohl am besten geeignet, obwohl es nicht die größte Fläche hat.)

Um aber bei das Rechteck / Tor mit dem nachweislich

(also nicht nur vermutet)

größten Flächeninhalt zu erhalten, brauchen wir eine Planskizze mit irgendeinem Rechteck, dessen Maße beliebig sind, solange sie die Bedingungen a. und b. erfüllen.

Nehmen wir also als Beispiel

(wobei wir alle Zahlen weglassen, die auf ein konkretes Rechteck hinweisen).

Nun können wir das Problem noch ein bisschen vereinfachen:

• der Flächeninhalt

  • vonist doppelt so groß

  • wie der Flächeninhalt von ;

• deshalb

  • ist der Flächeninhalt von genau dann maximal,

  • wenn der Flächeninhalt vonmaximal ist.

Und aus diesem Grund betrachten wir ab sofort nur noch bzw.

.

Für den Flächeninhalt A eines Rechtecks gilt A = Länge • Breite .

Wenn wir nun die Länge x nennen, ergibt sich:

Fragt sich nur, wie wir Länge und Breite in einen Zusammenhang gequetscht bekommen:

Da der Punkt P auf dem Funktionsgraphen liegt, hat er die Koordinaten x und f(x):

Damit ergibt sich für den Flächeninhalt 

Erinnern wir uns nun, dass in der Aufgabenstellung stand: f(x) = - x² + 4

Damit erhalten wir

Nun ist der A nur noch von der einzigen Variablen x (der Breite des Rechtecks) abhängig, und deshalb schreiben wir 

Das ist endlich die anfangs genannte "Zielfunktion" .

(Naja, wir haben wohl eher ein Zwischenziel erreicht, denn einige Rechnungen stehen uns noch bevor.)

Mit der Zielfunktion mit der Funktionsgleichung 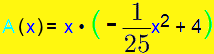sind wir nun in der reinen Algebra, können wir also für einige Zeit das Gewächshaus, aber auch die geometrische Darstellungkomplett vergessen.

Nun können wir mit dem Distributivgesetz noch die Klammer im Funktionsterm der Zielfunktion 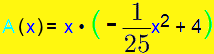beseitigen und erhalten dadurch

,

also eine ganzrationale Funktion dritten Grades.

Die einzelnen Rechnungen zur Ermittlung des Maximums der Zielfunktion seien hier nicht mehr vorgemacht

(diese Rechnungen sind Kinderkram!),

sondern nur soviel:

• durch die notwendige Bedingung für ein Maximum, nämlich A' (x) = 0, erhalten wir die beiden Lösungen x₁ = + ≈ 5,7735 und x₂ = - , wobei die letztere allerdings wegfällt, da wir in nur nach positiven Lösungen suchen.

• Wenn man x₁ = in A'' (x) einsetzt, zeigt sich, dass die hinreichende Bedingung für ein Maximum erfüllt wird, M ( | y ) also das Maximum der Flächenfunktion ist.

• Den y-Wert von M ( | y ) erhält man, indem man x₁ =  in die Ausgangsfunktion f(x) = - x² + 4 einsetzt, wodurch sich y = = 2,6 ≈ 2,6666 ergibt und somit  M ( | ).
• Dabei ist
  • die Breite und die Höhe des Rechtecks in
  • und somit • ≈ 15,396 dessen Flächeninhalt.

Nach diesem rein innermathematischen Rechnungen nun aber zur langsamen "Rückübersetzung" der mathematischen Ergebnisse in die Gewächshaus-Aufgabe. 

Vorsicht!: in der Aufgabenstellung geht es

• um
• und nicht um unsere zwischenzeitliche Vereinfachung !

Deshalb ergibt sich:

• die Breite des Rechtecks in ist 2 •  ≈ 11,547.
• Bei der Höhe des Rechtecks in ändert sich nichts, sondern sie bleibt   ≈ 2,6666.
• Der Flächeninhalt des Rechtecks in ist also 2 •  • ≈  2 • 15,396 ≈ 31,872.

Vorsicht!: wenn man nun zur Antwort auf die Aufgabenstellung kommt, beachte man dringend zweierlei:

• genau auf die Aufgabenstellung achten, also auf "Berechnen Sie die Maße des Tores und seinen maximalen Flächeninhalt";

• die Maßeinheiten m und m² nicht vergessen!

Wir übernehmen von oben, sprechen nun aber von der Breite (des Tores) statt von der Länge (des Rechtecks) und von der Höhe (des Tores) statt der Breite (des Rechtecks):

• die Breite des Tores ist 2 •  m ≈ 11,547 m ;
• die Höhe des Tores ist m ≈ 2,6666 m ;
• der Flächeninhalt des Tores ist 2 •  • ≈  31,872 .

Zum Abschluss antworten wir, indem wir uns zur Fehlervermeidung möglichst genau an den Wortlaut der Aufgabe bzw. der Frage halten:

Aufgabe: "Berechnen Sie die Maße des Tores                                                                 und seinen maximalen Flächeninhalt." 

Antwort:   "Das Tor            ist 2 •  m ≈ 11,547 m breit, m ≈ 2,6666 m hoch und hat den                    Flächeninhalt 2 •  • m² ≈  31,872 m²."

Unsere Schätzungen oben, also 10 für die Breite und 3 für die Höhe, waren also zumindest so gut, dass uns die rechnerisch hergeleiteten exakten Ergebnisse nicht völlig überraschen.

2.

Gegeben sind die Funktionen f und g mit f(x) = 3x • e-x und g(x) =  x  (vgl. Figur 1). Die Graphen beider Funktionen schneiden sich im Koordinatenursprung und einem weiteren Punkt   (vgl. Figur 2). Zwischen diesen beiden Punkten sei eine Parallele zur y-Achse gezeichnet, die die Funktionsgraphen von f und g in den Punkten P und Q schneidet (vgl. Figur 3). Der Koordinatenursprung , der Punkt P und der Punkt Q bilden ein Dreieck. Für welche Parallele zur y-Achse (welches x) ist die Fläche des Dreiecks am größten? Figur 1 vergrößert: Figur 2 Figur 3

Im Unterschied zu den Aufgaben 1., 3. und 4. gibt diese Aufgabe nichtmal vor, eine Anwendung auf irgendeinen Teil der außermathematischen Wirklichkeit zu sein, sondern hier spricht Mathematik nur über sich selbst.

(So gesehen ist diese Aufgabe wohl die ehrlichste der drei Aufgaben, denn die drei anderen Aufgaben sind ja doch wieder nur „eingekleidete“ Mathematik.)

Einschub für Lehrer: bei jeder Klausuraufgabe sollte ein Lehrer überlegen, was er abprüfen möchte - und was lieber nicht. Im vorliegenden Fall ließe es sich trefflich streiten, ob man die Figuren 2 und 3 (und evtl. sogar noch eine Figur 4, in der zusätzlich auch noch das Dreieck eingezeichnet wäre) mitliefern sollte oder ob die Schüler sie selbst entdecken sollten. Ich habe mich hier dafür entschieden, die Figuren 2 und 3 mitzuliefern, weil es mir bei der Aufgabe nur um das Auffinden der Zielfunktion geht, nachdem der geometrische Sachverhalt vorweg klar ist (Figur 4 habe ich aber nicht mehr mitgeliefert, weil nach Figur 3 eigentlich klar sein müsste, welches Dreieck gemeint ist). Ich habe die Aufgabe - ehrlich gesagt - gemopst. In der Originalversion lautete sie so: "Gegeben sind die Funktionen f und g mit f(x) = 3x • e-x und g(x) = x .  Die Graphen beider Funktionen schneiden sich bei x = 0 und xs.  Der Punkt P (u | f(u)), der Koordinatenursprung und der Punkt Q ( u | g(u)) bilden für 0 < u < xs ein Dreieck.  Für welchen Wert von u ist die Fläche dieses Dreiecks am größten?"  (die Quelle ist mir leider unbekannt; s.o.) Gleich drei nicht mal "schlechte" Nachhilfeschüler hatten aber mit dieser doch arg algebraisch-unanschaulich formulierten Aufgabenstellung enorme (hier nicht näher erklärte) Schwierigkeiten, haben meine variierte Aufgabenstellung aber auf Anhieb verstanden. Wie wir gleich sehen werden, bleiben das Auffinden der  Zielfunktion und deren ersten beiden Ableitungen dann noch immer ganz schön gehirnausrenkend.

In Figur 3 ist schnell das (?) gemeinte Dreieck eingezeichnet:

Nun ist da aber nur eine von unendlich vielen möglichen Parallelen zur y-Achse und damit auch nur ein Dreieck eingezeichnet, so dass

• an diesem einen gezeichneten Dreieck
• die Frage nach dem flächengrößten Dreieck (unter vielen Dreiecken) gar nicht aufkommen kann,

sondern die Existenz solch eines flächengrößten Dreiecks nur eine Behauptung in der Aufgabe ist.

(„wenn der Autor das behauptet, wird‘s wohl stimmen, und für eine gute Note würde ich sogar den größten [und uninteressantesten] Schwachsinn glauben“).

Wie schon in Aufgabe 1. bin ich aber der Meinung, dass es sich zum tieferen Verständnis der Aufgabe lohnt, anhand einer Planskizze mal eben auf die Schnelle eine dynamische Entwicklung aus mehreren Zwischenzuständen anzuschauen: 

Hier wird deutlich:

• wenn man die Parallele weit nach rechts schiebt , werden die Flächeninhalte der Dreiecke immer kleiner (gehen sie gegen null);
• wenn man die Parallele weit nach links schiebt , werden die Flächeninhalte der Dreiecke ebenfalls immer kleiner (gehen sie ebenfalls gegen null);
• wenn die Parallele irgendwo (genau???) in der "Mitte" (an einer einzigen Stelle?) ist, ist der Flächeninhalt also am größten. Unter unseren wenigen Beispielen scheint das bei der Fall zu sein, also bei x = 1.

Aber dieses Ergebnis „ bei x = 1“ ist eben nur ein Schätzwert, der

(wenn man‘s denn ganz genau nimmt)

aufgrund von Mess- und Zeichenungenauigkeiten auch falsch sein kann.

(Man wird ahnen, dass hier dasselbe Spielchen wie bei Aufgabe 1 losgeht - wenn sich die Lösungswege auch teilweise markant unterscheiden).

Um unsere weiteren Gedanken nicht an einem konkreten und evtl. nicht größtmöglichen Dreieck aufzuhängen, lassen wir die Einheiten auf den Koordinatenachsen mal weg:

Um das Dreieck mit dem größten Flächeninhalt zu finden, müssen wir zu allererst die Dreiecksfläche berechnen. Weil für die Fläche A eines Dreiecks gilt, wobei g eine der Grundseiten und h die Höhe darüber ist, müssten wir g und h berechnen. Nehmen wir uns also das Dreieck und drehen es erstmal so, um einen besseren Überblick zu erhalten, und zeichnen wir dann noch die Höhe ein: .

Relativ einfach wäre es noch, aus den Koordinaten von P mit dem Satz des Pythagoras die Länge der Dreiecksseite g zu berechnen. Aber die Berechnung der Höhe h wäre dann zwar ebenfalls möglich, aber doch enorm aufwändig.

Nun haben die Mathematiker ja ein besonders inniges Verhältnis zu Dreiecken und da insbesondere rechtwinkligen Dreiecken , bei denen die Berechnungen mit der Satzgruppe des Pythagoras und der Trigonometrie (Sinus, Cosinus ...) besonders einfach sind.

Gibt es also in vielleicht doch (sozusagen auf den zweiten Blick) rechtwinklige Dreiecke?:

• immerhin ist schonmal ein weiteres Dreieck erkennbar, das zudem (hurra!) rechtwinklig ist: ;
• außerdem bilden das hellblaue und das hellgrüne Dreieck zusammen ein drittes, ebenfalls rechtwinkliges Dreieck:

Es gilt also =  + .

Wenn wir das nun nach unserem gesuchten, leider nicht rechtwinkligen Dreieck auflösen, ergibt sich

,

womit wir immerhin schon mal durch die beiden rechtwinkligen und somit einfacheren Dreiecke und ausdrücken können.

Nun ist aber die Berechnung der Flächeninhalte rechtwinkliger Dreiecke besonders einfach, da bei ihnen eine Seite identisch mit der Höhe ist:

•   hat den Flächeninhalt

•   hat den Flächeninhalt .

Dabei haben allerdings und

• zwar dieselbe Grundseite g ,

• aber verschiedene Höhen h und h  !

Nun müssen wir nur noch die Grundseite und die Höhen der beiden Dreiecke und durch die Koordinaten der Punkte P und Q ausdrücken:

• weil P auf dem Funktionsgraphen der Funktion f liegt, gilt P ( x | f (x) ) = P ( x | 3x • e^-x ) , und deshalb ist x die Grundseite und 3x • e^-x die Höhe von . Der Flächeninhalt von ist also oder kurz

.

• weil Q auf dem Funktionsgraphen der Funktion g liegt, gilt Q ( x | g (x) ) = Q ( x | 3x • e^-x ) , und deshalb ist x die Grundseite und 3x•• e^-x die Höhe von . Der Flächeninhalt von ist also oder kurz

.

Wenn wir jetzt noch , und "zusammenschmeißen", erhalten wir

oder kurz

Da wir nun die Fläche A des Dreiecks in Abhängigkeit von der einzigen Variablen x haben, schreiben wir sie nun als Funktionsgleichung:

A ( x ) = • ( 3 x² • e ^-x ) - x²

Wenn man lustig ist, kann man darin noch die Klammer auflösen und erhält 

A ( x ) =          x² • e^-x   - x²

Damit haben wir nun endlich (!!!) unsere Zielfunktion  mit der Funktionsgleichung

Dieser Zielfunktion ist nun ihre Herkunft

(flächengrößtes Dreieck ...)

nicht mehr ansehbar, und entsprechend findet ab jetzt für einige Zeit nur noch Gleichungsjonglieren statt:

um die notwendige Bedingung für ein Maximum zu erkunden,

• wird die erste Ableitung bestimmt, wobei sich A ' (x) = 3 x • e^-x -  x² • e^-x -    x   ergibt

(hier sei nicht gezeigt, wie es schrittweise zu dieser Ableitungsfunktion kommt; nur soviel: da muss sowohl mit der Produkt- als auch mit der Kettenregel hantiert werden; vgl. );

• wird untersucht, für welche(s) x die Gleichung A ' (x) = 3 x • e^-x -  x² • e^-x -    x  = 0 erfüllt ist.

Nun lässt sich aus 3 x • e^-x -  x² • e^-x -    x noch mit dem Distributivgesetz x ausklammern, so dass wir erhalten:

      x           •    ( ) = 0

⇔ x = 0 oder       = 0

(Vgl. )

Wie die zweite Ableitung A ''

(die ich mir allerdings spare)

zeigen würde, liegt für x = 0 ein Minimum vor

(das in der Aufgabe aber nicht gesucht wird und selbstverständlich vorliegt, wenn x im Ursprung liegt und die Parallele auf der y-Achse).

Für welches x jedoch ist

= 0 ?

Ein Computer liefert für x den Näherungswert x ≈ 1,049, und die zweite Ableitung A '' würde zeigen, dass dort tatsächlich das gesuchte Maximum vorliegt.

Nach diesem reinen Rechnungsteil muss das Ergebnis wieder in die Dreiecksaufgabe rückübersetzt werden, und zwar wie gewohnt in maximaler Annäherung an die Aufgabenstellung:

• weil dort                   "Für welche Parallele zur y-Achse (welches x)              ist die Fläche des Dreiecks am größten?" gefragt worden war,

• ist die Antwort also "Für                                                                  x ≈ 1,049 ist die Fläche des Dreiecks am größten".

Unser obiger Schätzwert x = 1 war also

• zwar ziemlich genau,

• aber leider nicht der exakte Wert

(das wäre doch allzu schön gewesen).

Lange Rede, kurzer Sinn, bzw. was lernen "wir" aus dieser Aufgabe?:

Einschub für Lehrer: ich finde die Aufgabe (auch meine vereinfachte Version) in zweierlei Hinsicht unbefriedigend: , weil die erste Ableitung A  keine exakte, sondern nur eine ungefähre Lösung erlaubt, was zumindest ungeübte Schüler doch erheblich irritieren könnte; , weil in der Aufgabe zwei Schwierigkeiten kombiniert sind, die nichts miteinander zu tun haben:  , dass bei der Ableitung sowohl die Produkt- als auch die Kettenregel benötigt wird, das Jonglieren mit drei Dreiecken. Mir wäre b. wichtiger, und deshalb würde ich viel einfachere Funktionen f und g vorgeben, nämlich f: y = - x2 + 4x und g: y = x, bei denen sich dieselbe Frage nach dem Dreieck mit maximalem Flächeninhalt stellen ließe: Die Rechnungen dazu ergeben, dass für den bildschön einfachen Wert x = 2 (wenn also die Parallele durch den Scheitelpunkt der Parabel geht) die maximale Fläche vorliegt! Und bei solch einem erstaunlich einfachen Ergebnis kommt doch wirklich mal Freude auf: Noch interessanter wäre allerdings die Frage, wie sich die besonders einfache Lösung x = 2 im Laufe der Rechnungen zusammensetzt - und ob man sie nicht schon an den Funktionsgraphen, also ohne jede Rechnung hätte erkennen können.

Im Mathematik-Abitur werden oft zwei Aufgaben gestellt:

• eine zur Analysis (Ableitung / Integration),
• eine
  • entweder zur Vektor-/Matrizenrechnung
  • oder zur Wahrscheinlichkeitsrechnung

(also einer Auswahl aus den drei großen Themenbereichen der Oberstufenmathematik).

Eine typische Analysis-Aufgabe sieht dann z.B. so aus:

Es lohnt sich, solch ein Arbeitsblatt komplett durchzulesen oder zumindest doch zu überfliegen, bevor man überhaupt mit der ersten Rechnung anfängt.

Dann wird einem klar:

• es handelt sich um eine einzige Aufgabe, da alle Aufgabenteile sich mit der gleich im ersten Satz genannten Funktion f mit der Funktionsgleichung f (x) = (2 - x) • e^x  befassen.

Glücklicherweise ist diese Funktion noch relativ einfach, da zu ihrer Ableitung nur die Produkt-, aber nicht auch die Kettenregel benötigt wird.

Und doch ahnt man vielleicht schon, was bei schwierigeren Anfangs-Funktionen passieren kann: wer anfangs einen Blackout hat, hat bei sämtlichen Folge-Teilaufgaben kaum eine Chance mehr

(es sei denn, er bekäme Punkte dafür, dass er zwar nicht rechnet, aber doch erklärt, was zu tun wäre).

Und deshalb bin ich skeptisch bei solchen "Großaufgaben".

• Die Gesamtaufgabe besteht aus einer Hierarchie von Unteraufgaben

1. rein innermathematischer Teil (noch ohne Anwendung):

a) Ableitungsteil,

b) Integrationsteil,

2. Anwendungsteil c).

• Diese Teile sind nicht unabhängig voneinander, sondern
  • um zu zeigen, dass die in b) genannte Funktion F eine Stammfunktion von f ist, muss man Funktionen dieser Art ableiten können, also a) beherrschen;
  • in c) (2) wird das Ergebnis A(z) = (3 -z)•e^z - 3 aus b) (2) benötigt.

• Dennoch ist die Gesamtaufgabe nicht strikt linear aufgebaut, sondern z.B. ist die Teilaufgabe a) (3) ein kleiner Exkurs, der vom Weg abführt und dessen Ergebnis später nie wieder benötigt wird.

Und wenn die Wanne voll ist,
muss sie ja auch irgendwie voll geworden sein.

An der Gesamtaufgabe interessiert mich hier aber nur ein kleiner Teil, nämlich

und da eigentlich nur Aufgabenteil c), zu dessen Lösung man allerdings A(z) aus b) (2) braucht.

Dass diese Ölförderaufgabe eine Standardaufgabe ist, wird im Vergleich mit einer anderen Abituraufgabe deutlich:

Vorgabe: f (t) = 8 • t • e^{-0,25• t}

(Nebenbei: dass da die Formel nur hingeknallt, also weder [von den Schülern?] hergeleitet noch ansatzweise erklärt wird, ist symptomatisch für die Rezept-Mathematik, die heutzutage oftmals an Schulen herrscht: nix verstehen, aber alles einsetzen und stumpf damit rechnen.)

Hier wird von einer anderen, allerdings ähnlichen Funktion ausgegangen, und aus dem Öl im Tanklager ist die Wirkstoffkonzentration eines Medikaments im Blut geworden, aber letztlich ist da dieselbe Mathematik nur anders verpackt (versteckt) worden:

)

Damit aber zu

3.

Vorgaben: oder im Hinblick auf Aufgabenteil c) nur der Graph von f:

Wie schon oben gesagt: die Teile der Gesamtaufgabe

"[...] sind nicht unabhängig voneinander, sondern
[...]
in c) (2) wird das Ergebnis A(z) = (3 - z) • e^z - 3 aus b) (2) benötigt."

Aber dieser Rückbezug von c) (2) auf b) (2) wird in der Aufgabenstellung nicht ausdrücklich hergestellt, sondern man muss ihn selbst finden.

(Und doch könnte man sich ihn denken: es macht nur Sinn, am Ende von b) (2) "Zur Kontrolle: A(z) = (3 -z) • e^z - 3" zu schreiben, wenn dieses Ergebnis noch im Folgenden gebraucht wird. Es folgt aber eben direkt Aufgabenteil c).)

Wie ebenfalls schon gesagt: die Aufgabenteile a) und b) waren rein innermathematisch, in Aufgabenteil c) aber kommt eine "Anwendung", also erstmals, was oft "Textaufgabe" genannt wird

(und wovor viele Schüler große Angst haben).

Zur Bearbeitung von Texttaufgaben in der Analysis siehe .

Nun versteht aber doch kein Schwein diese Passage der Aufgabenstellung:

„c) Auf einem Erdölfeld wird Öl gefördert. Durch die Funktion f [also f: y = (2 - x) • e^x ] wird nun für 0 ≤ x  ≤ 2 die Förderrate¹ von Beginn des Jahres 2013 bis Ende des Jahres 2014 modelliert. Dabei wird x als Maßzahl der Zeit zur Einheit 1 Jahr und f(x) als Maßzahl der Förderrate zur Einheit 1 Millionen Tonnen pro Jahr aufgefasst.“

(Vgl. )

Deshalb ersetze ich die Passage durch

Erst danach folgt

(durch Kursivdruck hervorgehoben und im Vergleich mit der Aufgabeneinleitung erstaunlich kurz)

die eigentliche Aufgabenstellung:

Der Funktionsgraph von f zeigt für 0 ≤ x  ≤ 2 zu jedem (Zeit-)Punkt die jeweilige Fördermenge:

Wenn man nun all diese einzelnen Fördermengen aufaddiert, erhält man

(hellblau die jeweils hinzu kommende Fördermenge, rosa  die gesammelten vorherigen Fördermengen).

Insgesamt erhält man also als Gesamtfördermenge in den Jahren 2013 und 2014 die Fläche

.

Wenn man nun aber bemerkt, dass man jetzt bestens die in Aufgabe b) (2) hergeleitete Formel A(z) = ( 3 - z ) • e^z - 3 brauchen kann, ergibt sich für die gesuchte Fläche rasend schnell

A(2) = ( 3 - 2 ) •    e²  - 3 =

       =       1     •    e²  - 3 =

       =                   e²   - 3 ≈

       ≈               7,389 - 3 =

       =                4,389 

oder kurz

A(2) ≈              4,389

Um im Wortlaut auf die Aufgabenstellung

“Bestimmen Sie die für den gesamten Zeitraum von Beginn des Jahres 2013 bis Ende des Jahres 2014 zu erwartende Fördermenge.“

zu antworten:

„Die für den gesamten Zeitraum von Beginn des Jahres 2013 bis Ende des Jahres 2014 zu erwartende Fördermenge ist ungefähr 4 389 000 Tonnen.“

Es ist also letztlich sch...egal, in welche "Anwendung" die gemeinte Mathematik verpackt wird:

• statt um die gesamte Öl-Fördermenge von Beginn des Jahres 2013 bis Ende des Jahres 2014 (also in zwei Jahren)
• könnte es genauso gut auch um das Befüllen eines Swimmingpools zwischen 0 und 2 Uhr (allerdings nachts )
• oder um die Anzahl der Besucher in einem Fußballstadion zwischen Öffnung der Tore um 13.30 h und Spielbeginn um 15.30 (also innerhalb von zwei Stunden) 
• oder um das Füllen eines Messbechers gehen .

("Ölfördermenge" hört sich allerdings viel anspruchsvoller an, und 2013 - 2014 war wohl mal topaktuell, während Gläser etwa so häufig gefüllt werden, wie Reissäcke in China umfallen.) 

Einzig wichtig ist in allen genannten Beispielen die Metapher des "Befüllens" (und "Entleerens") , und zwar

• nicht, weil dieses Befüllen (und Entleeren) irgendwie anwendungsrelevant ist,
• sondern weil man sich die Mathematik hinter Aufgabe c) besser vorstellen kann.

Beim Befüllen (Entleeren) ist zu unterscheiden zwischen

• "Zulauf" ("Ablauf") (wieviel "fließt" gerade rein [raus]?)
• und "Füllmenge" des "Gefäßes" (wieviel ist schon [noch] drin?),

also

• ,

• ,

• → ,

• oder eben .

Die dritte Standardaufgabe ist demselben Arbeitsblatt entnommen wie die dritte:

4.

... wobei das Wort "linear" zu betonen ist.

Auch hier gilt wieder: f: y = (2 - x) • ex

Mit der Aufgaben (3) ändert sich die Situation vollständig:

• während in der dritten Aufgabe alles noch Zukunft war,
• ist es zum Ende des ersten Quartals 2014 bereits teilweise Vergangenheit :

Bis kurz vor Ende des ersten Quartals 2014 hat sich die Vermutung vom Beginn des Jahres 2013 bewahrheitet, dass die Erdölförderung sich wie die Funktion f verhält.

Mit dem Ende des ersten Quartals 2014 ändert dich das aber schlagartig: die Erdölförderung

• verhält sich nicht mehr wie f - - - ,

• sondern urplötzlich linear

(was in der Aufgabenstellung deutlicher betont werden könnte).

Da stellt sich doch die Frage, woran der Betreiber diese Änderung bemerkt hat, die

• sich einerseits seit einiger Zeit angekündigt haben muss,

• andererseits aber doch nur ein kurzfristiges Strohfeuer sein könnte.

Die Aufgabe ist also offensichtlich nur eingekleidete Mathematik. Z.B. (jede Wette) kommt das Ende des ersten Quartals vermutlich nur vor, damit man zu allem Überfluss auch noch das Rechnen mir Brüchen ( ) abprüfen kann.

Bei der Änderung der Fördermenge soll keine Lücke wie in entstehen

(mathematisch gesagt: die zusammengesetzte Funktion soll „stetig“ sein).

„keine Lücke“ bedeutet aber doch, dass

• die (Halb-)Gerade g da anfängt,

• wo der Funktionsgraph von f aufhört, also im Punkt .

Für gilt also: liegt auf dem Funktionsgraphen von f , muss auch auf der (Halb-)Geraden g liegen.

Damit haben wir schon unser halbes Rechenprogramm fertig.

Schauen wir uns jetzt noch anhand einiger Beispiele an, welche Möglichkeiten für g bleiben, wenn a. und b. erfüllt sind:

Es ist, als wenn in P ein Scharnier wäre, um das g sich dreht.

Welche dieser (Halb-)Geraden man nun verwendet,

• wird einerseits durch den nunmehr linearen Verlauf der Ölförderung nahegelegt

(hat sich der Verlauf abrupt oder anfangs unmerklich geändert?; und welche Richtung der Geraden deutet sich denn an?),

• kann aber auch eine rein ästhetische Frage sein.

Weil aber die Ölförderungs-Aufgabe sowieso an den Haaren herbeigezogen ist, erlaube ich mir eine ästhetische Betrachtung:

wieso eigentlich ist das

Cloud Gate

in Chicago derart beliebt, dass es geradezu zum Wahrzeichen der Stadt geworden ist?

Vermutliche Gründe sind doch

1. seine enorme Größe,
2. dass man - wie es sich für ein "gate" gehört - unten durch gehen kann,
3. die völlige Symmetrie,
4. die spiegelnde Oberfläche ohne jede Delle und Naht

(obwohl das Cloud Gate doch aus vielen Stahlplatten zusammengesetzt ist).

5. und zuguterletzt die handschmeichlerhaft abgerundete Form

(vgl. und ).

Die Besucher der "Cloud Gate" scheinen der vollständigen Harmonie nicht zu trauen, denn sie überprüfen andauernd, ob es wirklich "ohne jede Delle und Naht" ist und eine "handschmeichlerhaft abgerundete Form" hat, und zwar, indem sie

1. optisch nach „Fehlern“, also lokalen Verzerrungen innerhalb der Gesamtverzerrung, oder

2. mit den Händen nach Dellen, Ecken und Kanten suchen (und keine finden).

Die menschlichen Fingerspitzen sind aber derart feinfühlig, dass sie sogar die kleinsten Unregelmäßigkeiten erspüren:

(vgl. ;   ).

Jeder Schreiner, der irgendwas schleift, fährt ab und zu mit der Hand über das Holz , um auf diese Weise verlässlich alle Stellen zu finden, die noch nachgearbeitet werden müssen. Mit den Augen hingegen lassen sich verbleibende Unebenheiten nicht finden, da das Holz ja oft gemasert ist: .

 Was aber heißt das im Hinblick auf ?

Im Zweidimensionalen gibt es keine Kanten, wohl aber Knicke, nämlich z.B. bei

  (A)              (B)

(Man stelle sich die hier mit Nähnadeln illustrierten Ecken messerscharf  vor!)

Irgendwo in der Mitte zwischen den beiden eckigen Extremen (A) und (B) scheint es aber Varianten ohne Ecken zu geben:

(C) .               (D)

Woran aber liegt das hier in (C) und (D)  - und warum war das bei den beiden Extremen (A) und (B) nicht so?

Fangen wir mit einem ganz einfachen (Doppel-)Tisch an:

Wieso kann man sich

• am blauen Punkt herrliche blaue Flecken zuziehen,

• nicht aber am roten Punkt?

Das liegt daran, dass die Seitenkante

• im roten Punkt in derselben Richtung weitergeht, in der sie ankommt

,

• im blauen Punkt hingegen in einer anderen Richtung weitergeht, als sie ankommt

.

Da ist zu ergänzen:

• statt von „Richtung“ wird in der Mathematik von „Steigung“ gesprochen, so dass es dort heißt:

„[...] mit derselben (einer anderen) Steigung weitergeht, wie (als) sie ankommt.“

•  

  • während beim Tisch die Kanten gerade Strecken sind und deshalb auf langen Stücken dieselbe Richtung haben,

  • ändert sich die Steigung unserer „Ölfunktion“ andauernd:

Erinnern wir uns, dass "ankommen" und "weitergehen" genau bedeuten: "in ankommen und von aus weitergehen".

Von all den eben gezeigten Steigungen interessiert uns also nur die in :

Also muss gelten:

Die (Halb-)Gerade g und die "Ölfunktion" f  müssen in    dieselbe Steigung haben.

Damit haben wir zwei Bedingungen für die gesuchte (Halb-)Gerade g:

Wenn wir uns jetzt noch erinnern, dass

• "das Ende des ersten Quartals 2014" dem x-Wert (Jahre) entspricht , d.h. die x-Koordinate hat, woraus  ( | y ) folgt

(die y-Koordinate von ist hingegen noch unbekannt, muss also erst noch berechnet werden),

• f: y = (2 - x) • e^x ist   

• g eine Gerade sein, also die allgemeine Geradenform g: y = m • x + n haben soll

(wobei m die Steigung und n der y-Achsenabschnitt ist),

können wir vorsorglich auch schon die Ableitungen

(mittels derer man ja die Steigung berechnet)

erstellen:

• mit der Produktregel wird aus f  (x) = (2 - x) • e^x  die Ableitung f ' (x) = (1 - x) • e^x ,

• aus g (x) = m • x + n wird die hübsch einfache Ableitung g ' (x) = m .

Als "Ausgangsmaterial" für die folgenden Rechnungen haben wir also

Ein bisschen unübersichtlich ist daran die dritte Gleichung,

• die zwar eine einfache Geradengleichung ist,

• in der aber zusätzlich zu den üblichen Variablen x und y auch noch die Unbekannten m und n vorkommen.

Das liegt daran, dass wir ja noch nicht wissen, welche Gerade g passt, welche Zahlen also hinter m und n stecken.

Oder anders gesagt:

Unser Ziel ist es ja gerade, die passende Gerade g zu finden, also m und n überhaupt erst zu berechnen.

Hier liegt also eine Art "Steckbriefaufgabe" vor

(vgl. ):

• aus einigen vorgegebenen Bedingungen

(vgl. und )

• soll die bislang noch unbekannte Funktionsgleichung von g hergeleitet, sollen also m und n berechnet werden.

(Vgl.:

• mit Hilfe der im Steckbrief genannten Eigenschaften
• soll der Verbrecher Billy the Kid erkannt werden.)

Damit haben wir alle Zutaten für die weitere Lösung der Aufgabe - wobei gleich ergänzt werden muss:

1. ist es gar nicht so einfach, überhaupt erstmal all diese Zutaten zu finden;

2. gibt es einen gewaltigen Unterschied zur Herstellung eines Kuchenteigs:

• für einen Kuchenteig müssen die Zutaten meistens nur in beliebiger Reihenfolge zusammengeschüttet und dann zu einer homogenen Masse verrührt werden,
• zur Lösung der vorliegenden Mathematikaufgabe muss hingegen eine durchaus komplexe Reihenfolge eingehalten werden, und deshalb ist hier die Metapher eines Puzzles wohl doch passender: da müssen chaotisch angeordnete Puzzlesteine genau passend angeordnet werden.

Für viele Schüler mag der folgende (allzu suggestive?) Lösungsweg nachvollziehbar sein, aber wenn sie alleine vor solch eine Mathematikaufgabe wie die hier vorliegende gestellt sind, kommt ihnen alles wie ein einziges unstrukturiertes Chaos vor

(wie seinerzeit meinem Bruder   : oben fast die Hälfte ununterscheidbarer blauer Himmel, unten ebenfalls fast die Hälfte das Gewusel von hunderten Figuren während der „Alexanderschlacht“ [Gemälde von Albrecht Altdorfer];

es gibt aber bei Puzzles wie in der Mathematik Leute, die Spaß daran haben, durchaus mühsam, vielleicht aber auch entspannend das Chaos zu bändigen, und vielleicht kann man diesen Spaß sogar vermitteln).

Zwischendurch einige Tipps, wie man das Chaos in der vorliegenden Aufgabe ein wenig bändigen kann

(aber das sagt sich so leicht):

• aus der Aufgabenstellung alle mathematischen Aussagen heraussuchen und sie notieren;

(man merkt schon: Mathematik ist viel Schreibarbeit, aber diese Schreibarbeit nutzt vor allem einem selbst, damit man Überblick behält; die Schreibarbeit kann auch dazu führen, dass man in Klassenarbeiten Teilpunkte für Teillösungen bekommt, also z.B. wenn man zwar formulieren konnte, was man vorhatte, es aber nicht komplett rechnerisch durchführen konnte);

• aus der Aufgabenstellung alle Funktionsgleichungen heraussuchen und vorsorglich (je nach Aufgabenstellung evtl. mehrmals) ableiten (oder einmal integrieren); auch das schonmal sicherheitshalber notieren;

• Ziele formulieren und notieren (“was soll berechnet werden?“) und am Ende darauf zurückkommen (Antwortsatz);

• notieren, was Unbekannte bedeuten (z.B. „m ist die Steigung der Geraden g“);

• vorgegebene oder sich zwischendurch ergebende bekannte Werte (z.B. ) sofort in alle Gleichungen einsetzen, wodurch sich die Anzahl von Unbekannten in diesen Gleichungen reduziert (und eine Gleichung vielleicht sofort lösbar wird);

• Gleichungen, in denen nur noch eine Unbekannte vorkommt, sofort lösen (falls diese Gleichungen überhaupt lösbar sind);

• wenn in einer Gleichung mehrere Unbekannte vorkommen (die Gleichung also noch unlösbar ist), sofort nach weiteren Gleichungen suchen, in denen mindestens eine dieser Unbekannten vorkommt.

Aber natürlich macht erst Übung den Meister („Lehrjahre sind keine Herrenjahre“?).

Mit Hilfe von 

können wir uns nun daran begeben, die o.g. Bedingungen und in Gleichungen umzusetzen:

Nun ergänzen wir rechts die detaillierten Rechnungen:

Typisch Mathematik: auf komplizierten Wegen sind wir jetzt plötzlich doch bei sehr Einfachem gelandet:

2. 2,6177 = m                      • 1,25 + n
3.                 m =   -0,8725

Daraus folgt

   ,

In    2,6177   =         -0,8725  •  1,25 + n ist jetzt nur noch die eine Unbekannte n , die wir endlich auch noch ausrechnen können:

        2,6177   =         -0,8725  •  1,25 + n

        2,6177   =              -1,090625    + n   | + 1,090625

       3,7083   ≈                                       n

Damit haben wir unser erreicht, nämlich

Bleibt nur noch die letzte, langweilige Teilaufgabe, also „Berechnen Sie den Zeitpunkt, zu dem die Ölförderung enden wird“

(wozu sonst will man die Funktion g haben?!):

                    0 = - 0,8725 x + 3,7083    | - 3,7083

- 3,7083 = - 0,8725 x                    | : ( - 0,8725 )

       4,25 =                x 

Die Ölförderung endet also nach 4,25 Jahren.