Crashkurs
 Exponentialfunktionen
Exponentialfunktionen
| |
Wer hat denn gesagt, dass
Exponentialfunktionen einfach seien?
„Ein Teil des
Problems liegt darin, dass unser Denken gewissermaßen linear verdrahtet
und damit anfällig dafür ist, nur in begrenzten Dimensionen
stattzufinden. Dafür können wir nichts. Wir denken in Addition und
Multiplikation, einen Evolutionsdruck, exponentiell zu denken, hat es
nie gegeben. Ein Exponent ist eine Zahl, die zur Potenz einer anderen
Zahl erhoben wird. Bei diesem Rechenvorgang wachsen (oder schrumpfen)
die beschriebenen Größen oder Verhältnisse schneller, als es für unseren
normalen Verstand erfassbar ist.“
(Quelle:
 ) )
Man
kann also mit Exponentialfunktionen rechnen, sie aber nicht
verstehen, womit Exponentialfunktionen Sonden
 ins
Unfassbare sind. ins
Unfassbare sind. |
 benötigtes
Vorwissen
benötigtes
Vorwissen
 Exponentialfunktionen
Exponentialfunktionen
benötigtes Vorwissen:
-
Potenzen
Einen mathematischen Ausdruck der Form

nennt man „
Potenz“

. Die Zahl
a unten heißt „
Basis“,
die Zahl
b oben heißt „
Exponent“.
(Dringend empfohlen sei auch die Wiederholung der
 Potenzgesetze!)
Potenzgesetze!)
-
Funktionsarten
Der Begriff der „Funktion“ ist einer der absolut
zentralen Begriffe der Mathematik und Naturwissenschaften seit über 400
Jahren:
|
Eine Funktion ist eine eindeutige Zuordnung,
d.h. jedem x wird genau ein
y zugeordnet (und nicht mehrere
y). |
|
Es gibt verschiedene Funktionsarten mit
sehr unterschiedlichen Eigenschaften
(die Funktionsgraphen
sehen ganz anders
aus und die verschiedenen Funktionsarten werden völlig unterschiedlich abgeleitet).
Deshalb darf man die verschiedenen
Funktionsarten auf keinen Fall verwechseln: eine Gefahr, die
insbesondere dann naheliegt, wenn
(wie bei der
 ) )
verschiedene Funktionsarten in einer Aufgabe kombiniert sind.
Bevor man also losrechnet, überprüfe man insbesondere, ob die Variable
x
UNTEN in der
Basis oder
OBEN im Exponenten einer
Potenz steht.
|
Hier einige in der Schule
behandelten Funktionsarten:
- Potenzfunktionen,
- ganzrationale
Funktionen,
- gebrochen rationale Funktionen,
-
Exponentialfunktionen,
- trigonometrische Funktionen (z.B. die
Sinus-Funktion).
Von diesen verschiedenen Funktionsarten sollen uns hier
nur die farbig markierten interessieren,
also
-
Potenzfunktionen,
- ganzrationale Funktionen,
- Exponentialfunktionen.
Zu A., also den
Potenzfunktionen:
Potenzfunktionen haben Funktionsgleichungen der Form y =
c •
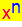
, wobei
n eine natürliche Zahl (inkl. 0) ist.
Entscheidend dabei ist, dass das
x unten
in der
Basis der
Potenz steht
(während das
x
bei den unten ausführlicher behandelten
Exponentialfunktionen
oben
im Exponenten der
Potenz steht).
Beispiele für
Potenzfunktionen sind

Hier lernen wir auch schon die „
Faktorregel“
für Ableitungen kennen, die für
alle Funktionen gilt
(unten also auch für
Exponentialfunktionen):
| |
Faktorregel:
wenn
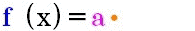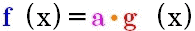 ist,
gilt für die Ableitung ist,
gilt für die Ableitung
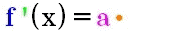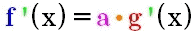 , d.h. die dranmultiplizierte
Konstante a wird beim Ableiten einfach
unverändert mitgeschleppt. , d.h. die dranmultiplizierte
Konstante a wird beim Ableiten einfach
unverändert mitgeschleppt. |
Ein Beispiel:
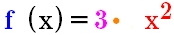
, also
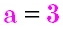
und
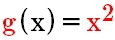
. Dann ist
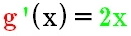
und folgt:
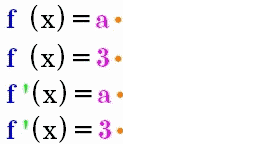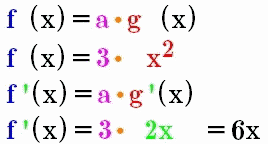
Zu B., also den
ganzrationalen
Funktionen:
Eine
erste Möglichkeit,
mehrere
Funktionen zu
einer zusammenzusetzen, ist die
noch sehr einfache
Addition oder
Subtraktion, also
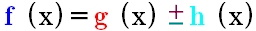
.
Die zweite Ableitungsregel, die auch wieder für
alle Funktionen gilt
(unten also auch für
Exponentialfunktionen),
ist
| |
die „Summenregel“: man leitet
die Summe (oder
Differenz) mehrerer Funktionen
ab,
- indem man die einzelnen Funktionen ableitet
- und dann alles addiert (oder
subtrahiert).
Oder anders gesagt: man schleppt „+“
und „-“ beim Ableiten einfach unverändert
mit:

|
Ein Beispiel, in dem wir schon drei Funktionen
addieren, und zwar die bereits oben genannten
Potenzfunktionen i: y = x2,
h: y = 6x und g: y = 8:
Dann gilt für die Ableitung
Addierte (oder
subtrahierte)
Potenzfunktionen
nennt man "ganzrationale
Funktionen"
(im Gegensatz zu "gebrochen
rationalen Funktionen; s.
 ).
).
Die ganzrationale
Funktionen sind spätestens seit der 8. Klasse immer wieder
durchgenommen worden. Insbesondere wurden an ihnen durchgenommen
-
die Funktionsgleichung y = mx + n linearer Funktionen, wobei m die Steigung
und n der y-Achsenabschnitt ist,
-
die Bestimmung der Nullstellen quadratischer Funktionen mit der pq-Formel
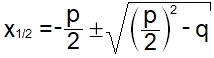
(lineare und quadratische Funktionen sind [mit ganz
wenigen Ausnahmen] die einzigen ganzrationalen Funktionen
, die wir lösen können [wenn sie überhaupt lösbar sind], und alle Funktionen
höheren Grades müssen [z.B. durch Polynomdivision] zu diesen
einfachen Funktionen zurechtgestutzt werden),
- die Ableitung und mit ihr die Bestimmung von Minima, Maxima und Wendepunkten,
- das Integral (Flächenberechnung).
| |
Besonders wichtig sind die Bedingungen für
Minima, Maxima
und
Wendepunkte, denn diese
Bedingungen gelten
genauso für auf andere Art
zusammengesetzte Funktionen und Exponentialfunktionen:
|
Zu diesen Bedingungen siehe

.
| |
Bedingungen für
Minima,
Maxima und
Wendepunkte muss man gründlich auswendig kennen und
anwenden können!!! |
Die Funktionsgraphen aller
ganzrationalen Funktionen
sind
(evtl. mit einigen "Schlenkern" in der Mitte)
-
bei höchstem geradem Exponenten
parabelförmig
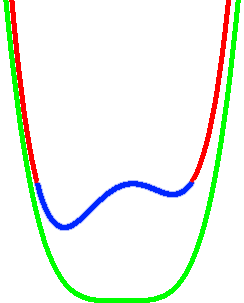 ,
,
Exponentialfunktionen:
- wie schon oben gesagt:
Potenzfunktionen haben Funktionsgleichungen der Form y =
c •
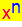 , wobei
n eine natürliche Zahl (inkl. 0) ist.
Entscheidend dabei ist, dass das x
UNTEN
in der Basis der Potenz steht. , wobei
n eine natürliche Zahl (inkl. 0) ist.
Entscheidend dabei ist, dass das x
UNTEN
in der Basis der Potenz steht.
- Bei Exponentialfunktionen
ist es umgekehrt: sie haben Funktionsgleichungen der Form y =
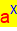 , wobei
a eine positive reelle Zahl ist.
Entscheidend dabei ist, dass das x
OBEN
im Exponenten der Potenz steht. , wobei
a eine positive reelle Zahl ist.
Entscheidend dabei ist, dass das x
OBEN
im Exponenten der Potenz steht.
(Im Folgenden behandeln wir
[mit Ausnahmen ganz am Ende]
nur die „nackten“ Exponentialfunktionen
, bei denen im Exponenten nur x und nichts anderes
steht. Bei der  werden
wir hingegen auch „zusammengesetzte“ Exponentialfunktionen
sehen, bei denen im Exponenten mehr als nur das
x steht.) werden
wir hingegen auch „zusammengesetzte“ Exponentialfunktionen
sehen, bei denen im Exponenten mehr als nur das
x steht.)
|
Zwei Beispiele:

Wenn man nicht weiß, wie der Graph einer Funktion aussieht,
oder wenn man wissen will, warum er eine bestimmte Form hat,
ist es ratsam, eine Wertetabelle aufzustellen. Dazu wähle man für
einfache Rechnungen ganzzahlige x rund um 0, weil alle in der
Schule durchgenommenen Funktionsgraphen sich dort besonders markant
verhalten:
Damit ergeben sich die beiden folgenden
Funktionsgraphen:
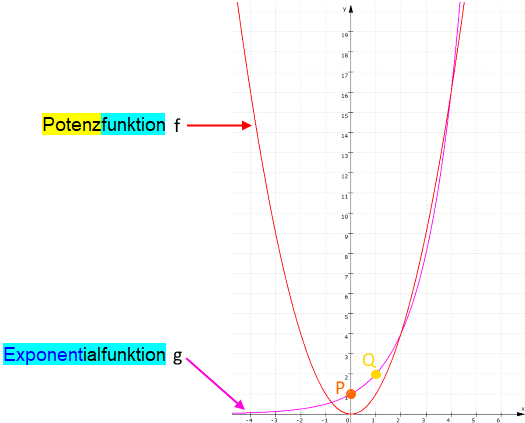
Daran sind
bereits markante Eigenschaften aller Exponentialfunktionen
der Form g: y =
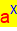 erkennbar:
erkennbar:
-
der Graph der Exponentialfunktion
g: y =
 geht durch zwei
markante Punkte, mittels derer man immerhin schon ansatzweise den Graphen zeichnen kann:
geht durch zwei
markante Punkte, mittels derer man immerhin schon ansatzweise den Graphen zeichnen kann:
-
durch P ( 0 |
1 ), der auch der Schnittpunkt des Graphen mit der y-Achse ist,
-
durch Q ( 1 |
2 ) ;
allgemein: die Graphen der
Exponentialfunktionen
g: y =
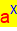 gehen
gehen
- alle
durch P ( 0 |
1 ) ,
- je nach Wahl von a durchQ ( 1 |
a ) :
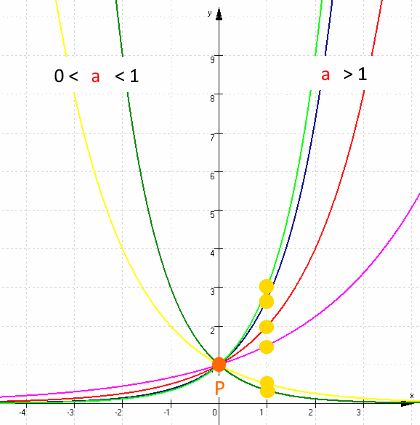
-
Schauen wir uns den Graph der Exponentialfunktion
g: y =
 nochmals genauer
an:
nochmals genauer
an:
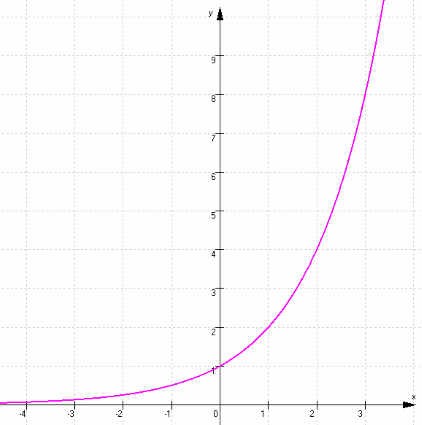
-
für
positive x, also rechts der y-Achse, verhält sich dieser Graph
ähnlich wie die Parabel einer
Potenzfunktion
(nur dass er für große x
sehr viel
rasanter ansteigt als jede Parabel, weshalb Exponentialfunktionen viel gefährlicher sind),
-
hingegen
verhält sich der Graph für negative
x, also links der
y-Achse, sehr ungewöhnlich: er geht immer näher an die
negative x-Achse, erreicht sie aber nie.
(Man sagt auch, dass
-
der Graph „asymptotisch“ gegen die
negative x-Achse geht
-
und die negative x-Achse die
„Asymptote“ des Graphen ist.
Dass der Graph unendlich nah an
die x-Achse heran geht, sie aber dennoch nicht erreicht, kann man sich mit
folgender Überlegung veranschaulichen:
-
man geht immer näher an eine
anfangs 100 cm entfernte Wand heran,
-
und zwar jeweils 90 % des vorherigen
Schritts.
Dann ergibt sich
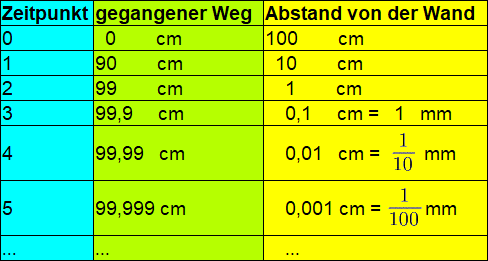
Auf diese Weise kommt man immer näher an
die Wand, erreicht [berührt bzw. durchstößt] sie aber nie.)
Allgemein: die Graphen von
Exponentialfunktionen
g: y =
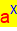 gehen
asymptotisch
gehen
asymptotisch
-
gegen die negative x-Achse für 0 <
a < 1
-
gegen die positive x-Achse für
a >
1.
Ein Beispiel aus der Coronakrise im Jahr 2020: die
Ausgangs- und Kontaktbeschränkungen, die viele Regierungen der Welt verhängt
haben, dienen dazu, die Neuansteckungen zu verringern - oder mathematisch
gesagt: die "Reproduktionszahl" R kleiner als 1 zu halten.
-
angenommen, R = 0,7, also 0 < R < 1; dann
fällt die Kurve der Neuansteckungen:
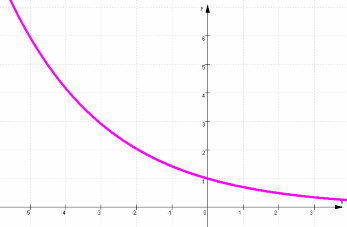
-
angenommen, R = 1,3, also
R > 1; dann steigt die Kurve der Neuansteckungen, und zwar auf die
Dauer dramatisch:
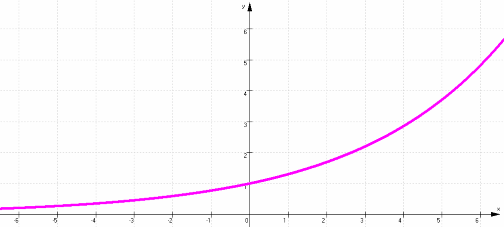
Die Graphen der Exponentialfunktionen
g: y =
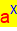 bleiben also vollständig oberhalb der x-Achse (die y-Werte also immer
positiv), woraus folgt, dass
Exponentialfunktionen KEINE
Nullstellen haben
bleiben also vollständig oberhalb der x-Achse (die y-Werte also immer
positiv), woraus folgt, dass
Exponentialfunktionen KEINE
Nullstellen haben
(was Rechnungen insbesondere in
 erheblich
vereinfachen wird)
erheblich
vereinfachen wird).
- Exponentialfunktionen
sind
(wenn man mit
x wie
immer
von links nach rechts geht

)
reine
Linkskurven

, woraus sofort folgt,
dass sie KEINE
Wendepunkte haben.
- Exponentialfunktionen
haben auch KEINE Extrempunkte (Maxima, Minima) und KEINE Sattelpunkte.
| |
Und wo nix ist, gibt's auch nix zu
berechnen. So gesehen sind Exponentialfunktionen
also extrem schülerfreundlich. |
- Das Zeichnen der Graphen von Exponentialfunktionen
bereitet dennoch einige Schwierigkeiten:
(wie oben gezeigt)
mit P ( 0 |
1 ) und Q ( 1 |
a ) zwei schöne Fixpunkte, mit denen man
die Zeichnung des Funktionsgraphen beginnen kann,
-
aber weil es natürlich nicht möglich ist, die
Graphen so zu zeichnen, dass sie sich unendlich nah an die x-Achse kuscheln, sie aber dennoch nicht berühren,
läuft man schnell Gefahr, dass die Graphen fälschlich
- entweder doch die x-Achse berühren oder sogar
schneiden, also eine oder mehrere Nullstelle(n) haben
(ein Fehler, den Computer gerne machen:
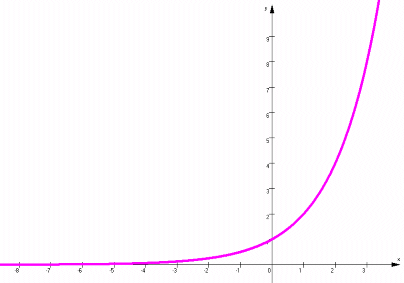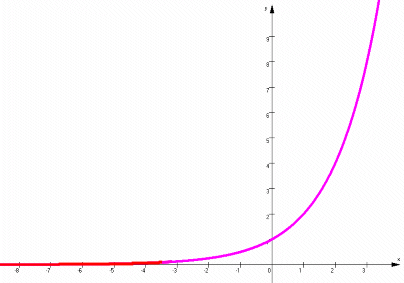 )
)
- oder doch wieder nach oben gehen.
Ich würde daher Graphen nur so weit zeichnen, dass der
asymtotische Trend deutlich wird, aber noch ein geringer Abstand zur x-Achse
bleibt.
- Oben war gesagt worden: „Jede
ganzrationale Funktion kommt links von
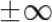 und geht
rechts nach
und geht
rechts nach 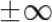 .“
.“
Exponentialfunktionen
hingegen kommen / gehen
- nur an einer Seite von / gegen +
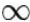
(jedoch nie von / gegen -
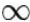
)
-
an der anderen Seite aber von der / gegen
die x-Achse.
- Nackte
Exponentialfunktionen besitzen
keine Punkt- oder Achsensymmetrie.
(Auch hier gibt‘s also nix zu berechnen!)
- Eine besonders interessante Exponentialfunktion
ist die „e-Funktion“ f: y
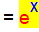 : für ihre
Ableitung gilt nämlich f
‘ : y
: für ihre
Ableitung gilt nämlich f
‘ : y
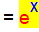 , d.h.
, d.h.
- es ändert durch das
Ableiten sich gar nichts,
- die Ableitungsfunktion f ‘ ist
also identisch mit der Ausgangsfunktion f.
(Man kann also beliebig oft ableiten [oder integrieren],
es kommt immer dasselbe raus. Und wenn sie nicht gestorben sind, dann leiten sie
noch heute ab [oder integrieren].
Nebenbei: die e-Funktion ist die einzige
Funktion im gesamten Funktionenuniversum, deren
Ableitungsfunktion identisch mit der Ausgangsfunktion
ist.)
Mit der Einfachheit der e-Funktion handelt man
sich aber auch eine Schwierigkeit ein:
für die "Eulersche
 Zahl" e gilt
Zahl" e gilt

Sie ist eine irrationale Zahl, also weder endlich noch
periodisch hinter dem Komma, und das hat zur Folge, dass man sie
-
nur beliebig genau annähern
 ,
,
-
aber niemals vollständig aufschreiben kann.
Deshalb belassen wir es in der Regel bei dem Buchstaben
"e", von dem wir eigentlich nur wissen müssen, dass sich dahinter eine feste
Zahl verbirgt
(dass e also keine Variable bzw.
Unbekannte wie x oder y
ist).
Wenn wir aber doch mal die Dezimalzahl brauchen, reicht
meistens e ≈ 2,7182 oder sogar nur e ≈ 2,7 , und wir überlassen es gnädigst dem Computer, mit sowas Fiesem zu
rechnen.
(e ist eine enorm wichtige Zahl:
-
sie taucht bei vielen natürlichen Prozessen auf
[vgl. z.B.
 ]
]
- und ist auch innermathematisch
hochinteressant

 .)
.)
"die e-Funktion ist die einzige Funktion im
gesamten Funktionenuniversum, deren Ableitungsfunktion
identisch mit der Ausgangsfunktion ist."
Daraus folgt, dass das Ableiten bei anderen
Exponentialfunktionen (also
z.B. y =
 ) nicht ganz so
einfach ist.
) nicht ganz so
einfach ist.
Glücklicherweise kann man aber diese anderen
Exponentialfunktionen
auf die e-Funktion zurückführen
Es gilt nämlich allgemein
... wobei ln
bzw. der „natürliche (!)
Logarithmus“ die Umkehrfunktion der
e-Funktion ist, diese also rückgängig macht
(genau so, wie
-
ein + ein - rückgängig macht [und umgekehrt],
-
ein : ein • rückgängig macht [und umgekehrt],
-
eine
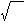 ein 2
rückgängig macht [und umgekehrt])
ein 2
rückgängig macht [und umgekehrt]) .
Hier soll der (natürliche) Logarithmus nicht genauer
besprochen werden
(und man muss ihn glücklicherweise auch gar nicht
verstehen, sondern es reicht
[wie auch weiter unten bei anderen Logarithmen],
wenn man es mit letzter Kraft noch schafft, auf dem
Taschenrechner die ln-Taste zu drücken).
Nur soviel:
-
gibt es verschiedene Logarithmenarten, also z.B.
auch den Zehnerlogarithmus, der auf Rechnern meist mit „lg“ abgekürzt
ist.
Man lasse den Finger von dieser lg-Taste!
-
sind die meisten Logarithmen auch wieder fiese irrationale
Zahlen
(s.o. bei der Eulerschen Zahl e),
so dass auch die meisten Computerergebnisse hinten
abgehackt, also ungenau sind, weshalb man nur noch mit einem ≈ statt einem
= weiterrechnen dürfte.
Und überhaupt: wer hat schon Lust, immer wieder z.B. die
Zahl 0,69314718 aufzuschreiben?!
Da ist es doch einfacher, den Ausdruck "ln(2)" mitzuschleppen, auch
wenn man keinen blassen Schimmer hat, welche Zahl sich dahinter verbirgt.
Wenn man dann aber doch mal die Dezimaldarstellung von ln(2) braucht, reichen meistens die ersten vier Nachkommastellen, also 0,6931.
Aber zurück zu
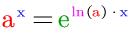 . Damit lässt sich nun auch
die Funktion f: y = ax ableiten
. Damit lässt sich nun auch
die Funktion f: y = ax ableiten
(die Herleitung mit der Kettenregel [vgl.
 ] spare ich mir hier mal):
] spare ich mir hier mal):
| |
f: y =
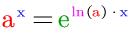 ⇒ f ' (x) =
⇒ f ' (x) =
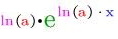
bzw.

Wo wir aber schon dabei sind, hier auch eine Stammfunktion
zu f: y = ax
:
f: y =
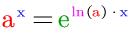 ⇒ F (x) =
⇒ F (x) = 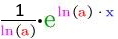
bzw.

|
Und wo wir aber gerade so schön beim Logarithmus sind, hier
auch noch eine andere wichtige Anwendung des Logarithmus:
angenommen mal, wir haben die Funktionsgleichung f:
y = 2x
-
: wir wollen wissen, welche Zahl
y die Gleichung
y = 210 löst. Dazu geben
wir sehr einfach 210
in den Rechner ein und erhalten y =
1024.
-
: wir wollen umgekehrt wissen, welche Zahl
x die
Gleichung 512 =
2x löst. Um das
herauszufinden, müssen wir x aus dem
Exponenten nach unten in die Basis
bekommen. Das geht mit dem einzigen Logarithmusgesetz, das man heute im
Zeitalter der Taschenrechner überhaupt noch braucht:
| |
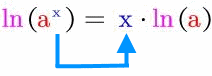
bzw.

|
Machen wir uns damit an die Lösung der Gleichung 512 =
2x :


Probe:
wenn wir 29
in den Taschenrechner eingeben, kommt tatsächlich 512
raus.
 Exponentialfunktionen
Exponentialfunktionen  Exponentialfunktionen
Exponentialfunktionen  )
) ins
Unfassbare sind.
ins
Unfassbare sind. . Die Zahl
a unten heißt „Basis“,
die Zahl b oben heißt „Exponent“.
. Die Zahl
a unten heißt „Basis“,
die Zahl b oben heißt „Exponent“.![]() Potenzgesetze!)
Potenzgesetze!)
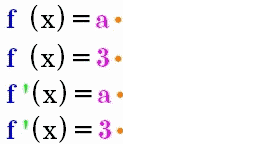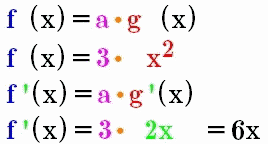
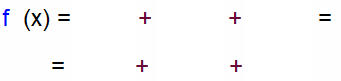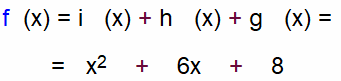

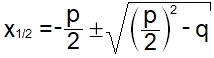
 ,
, .
.
![]() und
geht rechts nach
und
geht rechts nach
![]() .
.
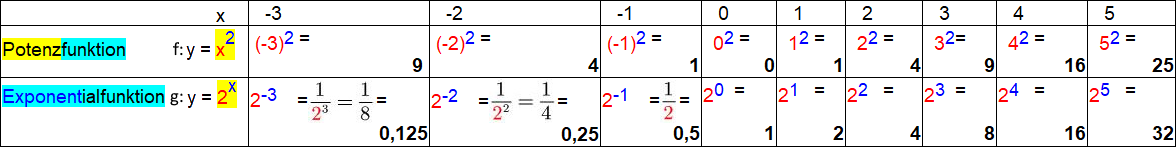






![]() bleiben also vollständig oberhalb der x-Achse (die y-Werte also immer
positiv), woraus folgt, dass
Exponentialfunktionen KEINE
Nullstellen haben
bleiben also vollständig oberhalb der x-Achse (die y-Werte also immer
positiv), woraus folgt, dass
Exponentialfunktionen KEINE
Nullstellen haben )
) , woraus sofort folgt,
dass sie KEINE Wendepunkte haben.
, woraus sofort folgt,
dass sie KEINE Wendepunkte haben. )
) Zahl" e gilt
Zahl" e gilt 
 ,
,

 .)
.)
![]() ) nicht ganz so
einfach ist.
) nicht ganz so
einfach ist.![]() . Damit lässt sich nun auch
die Funktion f: y = ax ableiten
. Damit lässt sich nun auch
die Funktion f: y = ax ableiten![]() ] spare ich mir hier mal):
] spare ich mir hier mal): 
![]()