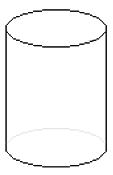
Flächen sind flach!?

"Glücklicherweise ist diesmal ein anderer schuld!"

Manchmal ist es durchaus wohltuend, SchülerInneN zuzuhören, die über den Mathematikunterricht anderer LehrerInnen reden:

• nicht etwa, um sich an der tatsächlichen oder vermeintlichen Unfähigkeiten dieser anderen LehrerInnen zu laben und aufzubauen

(und sowieso bin ich nicht so naiv, Äußerungen von SchülerInneN über andere LehrerInnen bedingungslos und ungeprüft zu glauben),

• sondern weil man da indirekt selbst den Spiegel vorgehalten bekommt:

da wird dann oftmals (wenn auch vielleicht aus sehr subjektiver Sicht) ehrlich gesagt, was (meine) SchülerInnen dem eigenen Mathelehrer (mir) aus (berechtigter?) Angst vor der Rache durch schlechte Zensuren nicht zu sagen wagen würden.

Anlass waren im hier besprochenen Fall die Klagen von SchülerInneN über eine bevorstehende Klassenarbeit zur "Raumgeometrie"

(Würfel, Quader, Prisma, Pyramide, Kugeln, Kegel, Zylinder: ).

Vordergründig schien das Problem darin zu bestehen, dass die SchülerInnen völlig konfus waren vor lauter Oberflächen- und Volumenformeln.

(Bzw. all die Formeln wurden nur unverstanden aus der Formelsammlung übernommen: so war weitgehend unbekannt, dass [und weshalb]

• in Flächenformeln meist ein Quadrat und in Volumenformeln meist ein Kubik vorkommt,

• Volumenformeln oft den Koeffizienten ¹/₃ enthalten

• und die Volumenformel für Kegel und quadratische Pyramide dieselbe, nämlich  ¹/₃ Grundfläche mal Höhe ist.

"Man" sah also - wenn überhaupt - nur Fakten, aber keine Struktur.

"Vordergründig" waren all die Probleme mit den Formeln aber vor allem, eben weil die SchülerInnen ja durchaus die Formelsammlung benutzen durften.)

Nach einigem Nachfragen stellte sich aber heraus, dass die (einige) SchülerInnen viel grundsätzlichere Probleme mit den Körpern hatten:

1. nicht nur, dass sie die Bezeichnungen durcheinander warfen (Kegel ↔ Zylinder),

2. sondern sie hatten auch keinerlei genauere Vorstellung von den Körpern.

Beispielsweise war überhaupt nicht die Grobunterscheidung bekannt zwischen

• senkrecht nach oben verlaufenden (Würfel, Quader, Zylinder, Prisma)

• und sich zuspitzenden Körpern (vgl. das oben genannte  ¹/₃ ) (Kegel, Pyramide).

Vor allem aber konnten die betreffenden SchülerInnen nur ansatzweise sagen, aus welchen Flächen (!) die betreffenden Körper zusammengesetzt sind.

Als ich zwecks Veranschaulichung meine gerade paratstehende (fast) zylinderförmige Kaffeetasse zu Hilfe nahm,

• sah jedeR SchülerIn noch, dass unten ein Kreis vorliegt - und oben (weil die Tasse ja oben offen ist) indirekt auch;

• konnte aber keineR sagen, was für eine Form die Seitenfläche (natürlich abgesehen vom Tassenhenkel) hat:

1. die einen sahen da zwar noch eine Fläche, konnten aber nicht deren Form benennen,

2. die anderen sahen da überhaupt keine Fläche.

Als Lehrer ist man bei solchen Ergebnissen erstmal versucht, über solch haarsträubende Unfähigkeiten mit den Ohren zu schlackern:

"Das darf doch nicht wahr sein, dass SchülerInnen nach langem Vorunterricht nicht mal die simpelste Anschauung haben!"

In einem zweiten Schritt denkt man

• entweder: "Die Jugend von heute wird auch immer blöder."

• oder: "Was für ein grausig schlechter Lehrer hat denn den Vorunterricht abgehalten?"

Dann erst - in einem dritten Schritt - wird man (ich) vorsichtiger und versucht zu verstehen, worin denn die Probleme liegen - und weshalb sie überhaupt zustande gekommen sind.

Gerade darin scheint mir ja das zentrale Problem zu liegen: wir (auch die meisten "guten") LehrerInnen haben die Mathematik schon allzu gut verstanden und können uns daher gar nicht mehr vorstellen, wo die Probleme der SchülerInnen liegen, also auch nicht bei diesen Problemen behilflich sein. Vielmehr bemerken wir diese Probleme oftmals überhaupt erst, wenn das Kind bereits in den Brunnen gefallen ist, sprich: die Klassenarbeit (mit grausigem Ausfall) geschrieben wurde.

(Im Folgenden sei mal davon abgesehen, ob man überhaupt

• im "Alltagsleben" die Seitenflächen von Körpern kennen muss [wohl kaum!],

• im Mathematikunterricht die Seitenflächen kennen muss, um eine Anschauung von den Körpern zu bekommen.)

Schauen wir uns also die Probleme noch mal genauer an:

1. die einen [SchülerInnen] sahen da zwar noch eine Fläche, konnten aber nicht deren Form benennen,

2. die anderen sahen da überhaupt keine Fläche.

Zu a.:

1. ist die Seitenfläche eines Zylinders ja auch gar nicht so eindeutig klar, denn unter vielen Möglichkeiten gibt es immerhin z.B. auch folgende:

(also ein Rechteck)

(also ein Parallelogramm)

2. fragt man sich aber doch, ob denn die SchülerInnen jemals vorher

1. im Mathematikunterricht Zylinder (wortwörtlich!:) abgewickelt oder umgekehrt aus Flächen zusammengesetzt (aufgewickelt, selbst gebastelt) haben

(und wohlgemerkt: unter "abwickeln" verstehe ich eine Tätigkeit, d.h. es reicht da nicht, Anfangs- und Endzustand vorzuführen;

und besser noch, als z.B. einfach das "sowieso" flache Papier von einer zylindrischen Verpackung abzurollen, ist es allemal, beispielsweise die Außenwand einer Konservendose regelrecht plattzuwalzen: );

2. sowas jemals im Alltag wenn schon nicht getan, so doch immerhin gesehen (aufmerksam wahrgenommen) haben:

Wenn weder A. noch B. der Fall war: wie sollen die SchülerInnen es denn auch können bzw. "sehen"?!

Nun drehe man aus der Unkenntnis der SchülerInnen nicht sofort dem Lehrer einen Strick: vielleicht hat er ja einfach B. vorausgesetzt und ist gar nicht auf die Idee gekommen, dass SchülerInnen beim Erkennen der Körperflächen Probleme haben könnten, diese also im Unterricht explizit zu behandeln wären.

(Merkwürdig fand ich allerdings den Kommentar des Lehrers, solche Körper seien doch ganz anschaulich anhand von Modellen in der 5. Klasse durchgenommen worden. Als wenn SchülerInnen sich fünf Jahre später noch daran erinnern könnten!

Die beste Reihenfolge ist doch wohl noch

1. reale [also dreidimensionale] Körper,

2. zweidimensionale Projektionen [Zeichnungen] dieser Körper,

3. nur noch Worte über Körper.

Dabei ist die Abstraktion des 3. Schritts [also ] natürlich ungemein wichtig, aber mir wird doch allzu schnell zu ihm hin gesprungen

[weil die LehrerInnen die vorherigen Schritte oftmals tatsächlich nicht mehr brauchen],

und man sollte auch immer wieder zurückspringen bzw. zwischen 1. bis 3. hin- und herspringen.)

Egal also, ob die Jugendlichen heutzutage tatsächlich immer weniger einschlägige Alltagserfahrungen haben  (nochmals: ) oder ob solche Vorstellungen schon immer ein Problem waren: wir brauchen erheblich mehr Modellbau im Mathematikunterricht, es sollten wiederholt die o.g. Körper gebastelt werden (vgl. ).

Zu b.,

also dass einige SchülerInnen an der Seite der Kaffeetasse überhaupt keine Fläche erkannten.

Die erste Reaktion ist da natürlich: "Ja, sind die denn mit Blindheit geschlagen?"

Aber dann höre man doch mal genauer hin!:

"Die Seite ist doch gebogen, also kann sie keine Fläche sein, denn FLäCHEN SIND - wie der Name schon sagt - FLACH!" ... und die Erde ist eine Scheibe:

Das ist in der Alltagssprache durchaus richtig, und die Fachsprache müsste doch erst ganz am Ende kommen:

Fläche, ebenes [!] oder beliebig gekrümmtes [!] Gebilde im Raum, insbesondere jede Begrenzung (Oberfläche) einer räumlichen Figur. In der Mathematik wird als Fläche eine Menge von Punkten im Raum definiert, zwischen deren Koordinaten eine feste, bestimmten Stetigkeitsforderungen genügende Beziehung besteht. Sie wird durch eine Gleichung bestimmt (z.B. durch eine algebraische Gleichung bei den algebraischen Flächen). Die Ordnung einer Fläche wird durch den Grad der sie beschreibenden Gleichung angegeben: Flächen erster Ordnung sind die Ebenen [hier haben wir also die Defintion, die in meist in der Alltagssprache benutzt wird], Flächen zweiter Ordnung z.B. Kugel, Kegel, Zylinder, Ellipsoide, Hyperboloide und Paraboloide. Besondere Flächen sind u.a. abwickelbare Flächen und Schraubenflächen.
(Brockhaus)

(Nunja, bei einer Kugel spricht man ja auch von einer [gebogenen, krummen!] Oberfläche!)

Mir scheint aber, dass der "Fehler", dass keine Fläche vorliege, weil Flächen ja flach seien, vermeidbar wäre, wenn man "Abwickeln" als Tätigkeit (s.o.) verstehen würde.