Funktionen interpretieren

Schon beim Titel "Funktionen interpretieren" wird der einen Hälfte der Menschheit, nämlich einseitigen MathematikerInneN, schlecht werden:

"Pfui Spinne, wir  müssen schon im Fach Deutsch andauernd »interpretieren«, also irgendwie [???] rausfinden, was der Dichter »damit« gemeint haben mag bzw. [wichtiger noch] was die Lehrkraft dafür hält. Und jetzt soll das auch noch in der Mathematik passieren?!"

(Und der anderen Hälfte der Menschheit, den notorischen Mathe-Verächtern, wird bei der anderen Hälfte von "Funktionen interpretieren", also bei "Funktionen", schlecht.)

Viele SchülerInnen (vielleicht sogar insbesondere die fleißigen) können zwar alle notwendigen (schematischen) Rechnungen zur "Funktionsdiskussion" durchführen

(also Einzelheiten bestimmen: Nullstellen, Schnittpunkte mit der y-Achse Minima, Maxima, Wendepunkte, Rechts- und Linkskurven ...),

aber das bleibt - weil reine Rechnung - meist völlig zersplittert, d.h. daraus ergibt sich kein Überblick über

• die gesamten Funktionsgraphen

• und damit auch die wesentlichen Eigenschaften (die Dramatik) der jeweiligen Funktionen.

Und wehe, wenn sie sich dann doch mal verrechnen: sie haben keinerlei Korrektur durch ein anschauliches Grundverständnis von Funktionen

(vgl. ).

Oder umgekehrt: sie wissen oftmals nicht vorher, was überhaupt rechnerisch rauskommen kann

(wonach sie suchen sollten - und wonach nicht)

bzw. muss

(z.B. dass eine ganzrationale Funktion dritten Grades garantiert eine Nullstelle hat, aber höchstens drei; oder dass solch eine Funktion immer -förmig aussieht - aber [wie jede Funktion] nie senkrecht wird).

Nun bin ich natürlich immer für die reine Lehre (reine Mathematik), aber das mangelnde Verständnis von SchülerInnen liegt oftmals auch darin begründet, dass sie keine Anschauung

(ungleich Anwendung; vgl.  "Anschauung statt Anwendung" )

haben. Ihnen fehlen die "tragenden Metaphern", also beispielsweise der Propeller als Metapher für Funktionen dritten Grades.

Die Schulmathematik lässt sich zwar ab und zu durch Anwendungen bestätigen

(vgl. etwa    ),

aber

1. hat das mit echten Anwendungen meist rein gar nichts zu tun

(was ich auch gar nicht schlimm finde, außer, es wird als Anwendung verkauft),

2. schnorrt mir die Schulmathematik - zwecks Veranschaulichung - doch allzu selten bei den Anwendungen.

Beispielsweise bleiben Funktionsgraphen völlig undramatisch, wenn man sie rein innermathematisch betrachtet:

"Da liegt ein Maximum oder ein Wendepunkt vor? Ja, schön und gut, aber was soll´s?!"

Wenn man aber - von mir aus rein fiktiv - beispielsweise die Entwicklung von Firmenfinanzen anschaut, entwickeln die abgenagt-isolierten Punkte plötzlich - und zwar durch den Kontext bzw. das Intervall, in dem sie liegen - echte Dramatik:

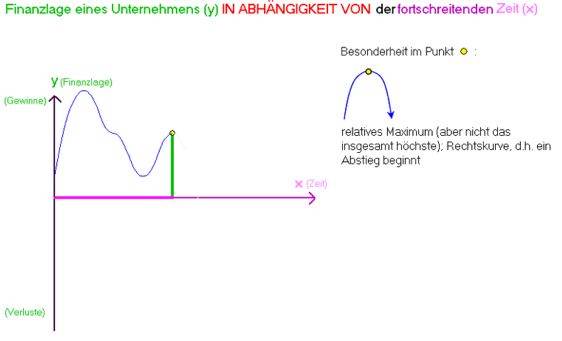
(vgl. und dort "Funktionsverlauf (Gewinne)")

"Maximum" hört sich so toll an, aber

1. liegt das hiesige relative Maximum weit unter dem früheren absoluten Maximum

(die Firma ist auf die Hälfte des ehemaligen Vermögens heruntergewirtschaftet worden!)

2. nach einem Maximum geht´s garantiert wieder bergab, d.h. ein Maximum ist wahrhaft kein Anlass zur Freude.

Vgl. auch die "Gedanken eines Investors":

2. Viel interessanter als die vordergründig bedeutsamen Maxima und Minima sind die Wendepunkte, weil sie eine Trendwende signalisieren und somit 

• frühzeitig (trotz einer vordergründig vielversprechenden Aufwärtsbewegung) vorwarnen

• bzw. umgekehrt (trotz einer beänstigenden Abwärtsbewegung) Mut machen:

Wie bereits gesagt: aus guten Gründen (nämlich zur Veranschaulichung von Innermathematischem) und völlig egozentrisch klaut die Mathematik gerne bei Anwendungen - aber eben nur das, was ihr ins System passt bzw. sie bestätigt.

Bzgl. Funktionen heißt das: die (Schul-)Mathematik beschränkt sich auf jene "einheitlichen"

(einfachen, nach einer einzigen und überhaupt einer Regel verlaufenden, als Funktionsgraph ästhetischen - oder abgenagten)

Funktionen - die nur leider

(mit wenigen Ausnahmen, beispielsweise )

kaum je so in der "freien Wildbahn" (Anwendungen) vorkommen

(wie ja auch die platonischen Idealgegenstände der Schulgeometrie, also z.B. Kreise, kaum so in "freier Wildbahn" vorkommen - und doch ein schönes Abstraktionsmittel sind).

Nun ist es aber durchaus erstaunlich, dass die Mathematik dennoch (zumindest teilweise) die komplexeren Funktionen der "freien Wildbahn" erfassen kann, beispielsweise - hier nur ohne Erklärung erwähnt - durch (allerdings in der Schule kaum je vorkommende)

• Fourier-Analysen (vgl. etwa  )

• oder Fraktale (vgl. das Mandelbrot-Buch unten sowie auch dreidimensionale Fraktale ).

Trotz meiner Vorliebe für die reine Mathematik kommen mir nun aber "echte" Funktionen viel zu selten im Matheunterricht vor. Sie scheinen mir aus mehreren Gründen wichtig:

1. damit SchülerInnen merken, dass Funktionen allüberall in der "freien Wildbahn" und keineswegs - was ja oftmals der Eindruck im üblichen Matheunterricht sein muss -  nur im Schulunterricht auftauchen;

2. , weil das zentral Wichtige an Funktionen (vor jeder Rechnung bzw. überhaupt Berechenbarkeit) sehr wohl oder vielleicht sogar noch besser an diesen Funktionen "aus freier Wildbahn" zeigbar ist, nämlich z.B. Eindeutigkeit oder - wie oben beschrieben - die Dramatik der Punkte.

3. und mir hier am wichtigsten ist aber, dass nur an solchen Funktionen aus "freier Wildbahn" eine Funktionsinterpretation sinnig ist:

Jeder (?) weiß:

• "Ich glaube nur Zitate, die ich selbst aus ihrem Zusammenhang gerissen habe." (Altbundespräsident Johannes Rau),

• "Ich glaube nur - pfui Spinne! - »Evaluationen« und »Qualitätsmanagmentzerifikate«, die ich selbst geschönt habe."

• "Ich glaube nur Statistiken, die ich selbst gefälscht habe"

(vgl. etwa oder ),

• und vielleicht auch noch, dass ich die Dramatik jedes Funktionsgraphen (also beispielsweise die Entwicklung der Arbeitslosenzahlen) übertreiben oder verharmlosen kann, je nachdem wie ich ihn im Koordinatensystem positioniere

(ob  ich also das Gesamtgebirge zeige, aus denen die Spitzen kaum herausstechen, oder nur die Spitzenregion, in der sogar jede kleinste  Neben-Zacke dramatisch erscheint).

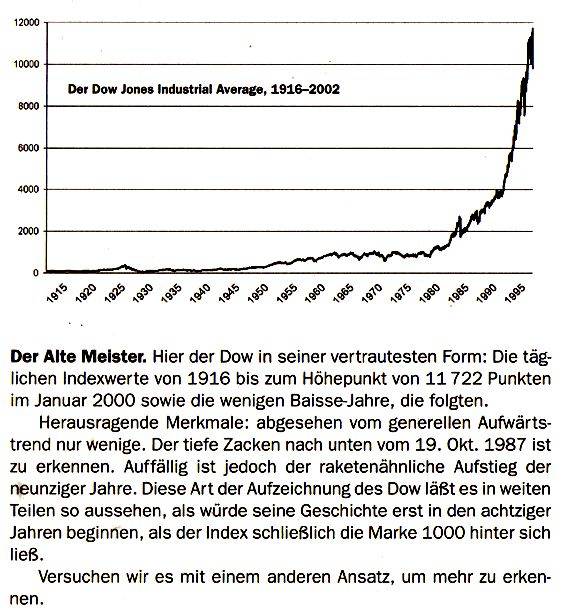
In seinem (sowieso lesenswerten) Buch und darin auf S. 136ff zeigt nun Benoit Mandelbrot sehr schön am Beispiel des Aktienindexes "Dow Jones", wie man Funktionsgraphen anderweitig schön fälschen oder - harmloser gesagt: - interpretieren kann bzw. wie man mit einer naiven Sichtweise schnell auf Einseitigkeiten herein fällt.

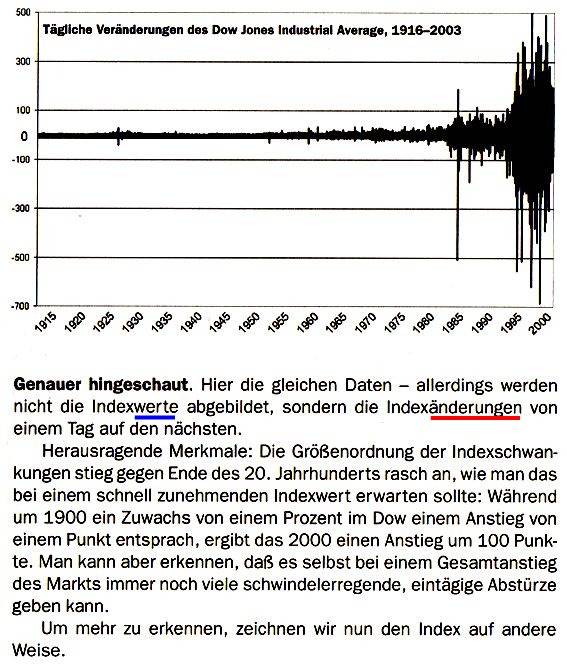
(Nebenbei: Indexänderungen, das ist schon die 1. Ableitung, woran man wieder - wie oben bei den Wendepunkten - sieht, dass der Umweg aussagekräftiger sein kann als das auf Anhieb Sichtbare.)

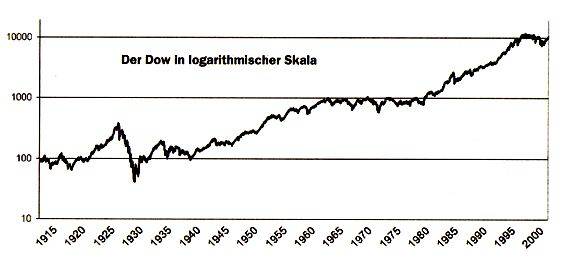
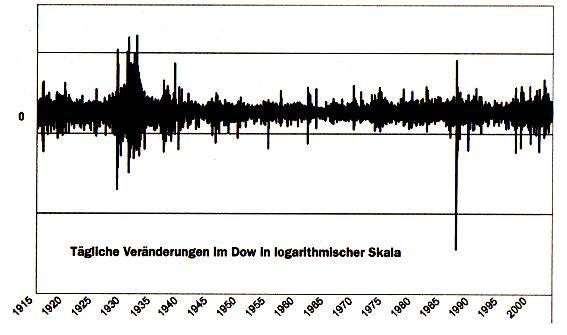
("logarithmisch abgebildet" bedeutet dabei kurz gesagt, dass die Zahlen auf der vertikalen y-Achse nicht in gleichen Abständen, sondern zunehmend gestaucht liegen:

Das hat dann beispielsweise zur Folge, dass die Graphen von Exponentialfunktionen nicht mehr immer rasanter ansteigen, sondern Geraden, also "handhabbarer" sind:

[Nebenbei: Logarithmuspapier hat auch folgenden Vorteil: wenn man die (z.B. Mess-)Werte einer noch unbekannten Funktion auf Logarithmuspapier zeichnet und dabei eine Gerade herauskommt, sieht´s schwer danach aus, dass eine Exponentialfunktion vorliegt. Und man kann sofort auch sehr einfach die Basis (y-Wert bei x = 1) ablesen.]

... woran ich vor allem erstaunlich finde, dass die scheinbar willkürliche und allemal komplizierte logarithmische Umsetzung mit "echtem Erleben" korrespondiert, nämlich "die Kursaufzeichnungen so aussehen [lässt], wie der Markt auf jemanden wirkte, der ihn real miterlebte.")

Quintessenz: ohne viel Mathematik (auf den ersten Blick) ist der Dow-Jones-Verlauf extrem dramatisch, mit komplizierterer Mathematik harmlos.