man muss Funktionen sehen:

1. : meine hochverehrte Fachleiterin im Referendariat würde natürlich auch hier sofort wieder einwenden:

"Herr Stauff, Sie meinen offensichtlich nicht Funktionen, sondern deren Funktionsgraphen, und befleißigen Sie sich deshalb doch bittschön gegenüber den SchülerInneN einer exakten Terminologie!"

Als wenn nicht auch und gerade die überexakte Terminologie

(z.B. "Zeichne an den Funktionsgraphen der Funktion f mit der Funktionsgleichung f: y = x² im Punkt P (2 | ? ) die Tangente" statt "Zeichne da [Finger drauf] die Tangente")

bei den SchülerInneN zu heilloser Verwirrung führen könnte!

Kommt hinzu, dass Funktionen arg abstrakte Dingsbumse sind, die man überhaupt nur mit Funktionsgleichungen und -graphen auf zwei unterschiedliche Arten "fassbar" machen kann!

2. : "Funtionen sehen"

(also überhaupt eine Vorstellung von ihrem Verhalten bekommen)

heißt zumindest für den Anfänger doch wohl: ihre Funktionsgraphen sehen!

(der Fachmann stellt sich, wenn er Funktionsgleichungen sieht, deren Funktionsgraphen wohl als innere Bilder vor oder hantiert überhaupt nur noch mit abstrakten, also nicht anschaulich vorgestellten Funktionsgleichungen)!

3. : "man muss Funktionen sehen". Alle?

 "[...] there's a great clarity,
as well as a kind of elegance,
in mathematical equations that is difficult,
if not impossible,
to express in words [oder anschaulichen Bildern].
It's a bit like trying to convey the majesty
of Mount Everest or Niagara Falls
without any pictures."
(Quelle:   )

Nein, es gibt natürlich auch eine rein rechnerische, also unanschauliche Schönheit. Eines der berühmtesten Beispiele ist, dass die e-Funktion y =

(nebenbei als einzige Funktion)

identisch mit ihrer Ableitung ist, dass also gilt: f: y = f ' = .

Das ergibt sich rechnerisch, und es läßt sich sogar sehen (veranschaulichen), was das bedeutet, nämlich

 , 

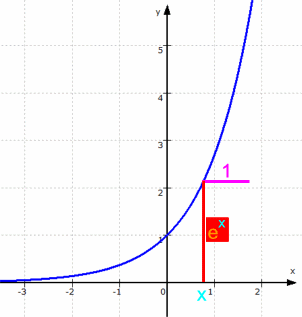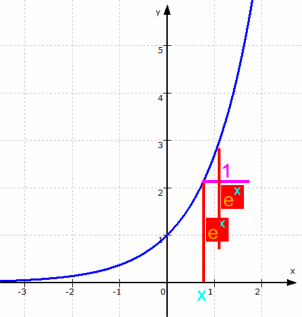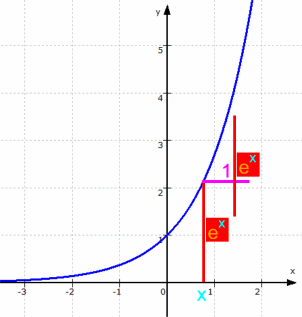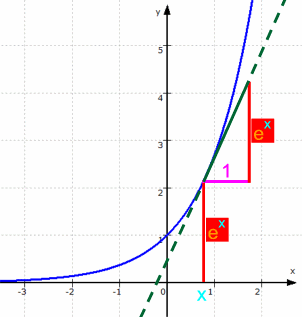aber es lässt sich

(zumindest meines Wissens)

nicht sehen (veranschaulichen), warum das so ist.

Die Aufgabe, die Anlass für meine Gedanken hier war, habe ich in zwei leicht unterschiedlichen Versionen im Internet gefunden

(wo genau, weiß ich nicht mehr):

1. "Gegeben seien zur y-Achse symmetrische quadratische Funktionen durch den Punkt P ( 1 | 1). Welche dieser Funktionen schließt mit der x-Achse eine minimale Fläche ein?"

(Nebenbei: überkorrekt gesprochen müsste hier ja wohl auch immer von "Funktionsgraphen" die Rede sein.)

2. "Gegeben seien zur y-Achse symmetrische quadratische Funktionen durch den Punkt P ( 1 | 1). Welche dieser Funktionen schließt mit der x-Achse eine extremale Fläche ein?"

Auch wenn "extremal" ein bisschen abgedreht klingt, gefällt mir doch die zweite Version schon ein wenig besser, weil da

• zwar verraten wird, dass es ein Flächenextremum gibt,

• aber noch nicht, ob da ein Minimum oder ein Maximum vorliegt.

Lieber wäre mir allerdings die noch offenere Aufgabenstellung

3. "Gegeben seien zur y-Achse symmetrische quadratische Funktionen durch den Punkt P ( 1 | 1). Vergleiche die Flächen, die die Funktionen mit der x-Achse einschließen!"

Die Aufgaben 1. und 2. lassen sich rein rechnerisch lösen, während bei der 3. Aufgabe mit "Flächen" zwar auch das rechnerische Integralverfahren angedeutet, vor allem aber doch nach dem Aussehen der Flächen

(also nach Verständnis!)

gefragt wird

(oder genauer: hier wird Verständnis überhaupt erst provoziert).

Die rein rechnerische

(hier nicht vorgeführte)

Lösung

(es gibt in der Tat ein [einziges] Flächenminimum)

funktioniert allerdings (sogar!) ohne jedes inhaltliche Verständnis der Funktionenschar und der Flächen unter den Einzelfunktionen: man bemerkt nicht,

• wie die Einzelflächen aussehen,

• wie sie kontinuierlich schmaler, dafür aber höher werden,

• wie das Minimum sich als logischer Zwischenwert zwischen zwei "Maxima" ergibt,

• vor allem aber: wie geradezu ästhetisch sich die Funkionsgraphen bewegen

(was ja überhaupt der einzige Reiz dieser Nicht-Anwendungs-Aufgabe ist).

Die pure Rechnung ist also witzlos bzw. regelrecht autistisch

(und dennoch typische Schulmathematik, also das Abspulen von Rechenrezepten ohne jegliches Verständnis - womit die Aufgabentypen 1. und 2. ideal für das stumpfe Zentralabitur wären, während keiner es wagen würde, dort die dritte Aufgabe zu stellen).

Aus den Vorgaben der Aufgabe(n) ergibt sich, dass

1. wegen der y-Achsen-Symmetrie die Funktionen nicht nur durch den in den Aufgaben bereits genannten Punkt P ( 1 | 1 ), sondern auch durch den "gegenüber" liegenden Punkt Q ( -1 | 1 ) gehen:

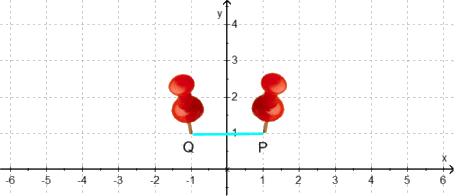
(um doch mal kurz "rechnerisch" zu werden: die Funktionsgleichungen müssen wegen der y-Achsen-Symmetrie f: y = ax² + b [ohne ungerade Exponenten] lauten, sind also bereits erheblich vereinfachte quadratische Gleichungen),

2. als nach unten geöffnete

(womit a negativ ist, wir also vielleicht doch besser y = - ax² + b mit dann allerdings positivem a schreiben)

Parabeln also etwa so aussehn:

Mit den Informationen 1. und 2. zusammen lassen sich ein erster Funktionsgraph wunderbar einfach

(und ohne jede Rechnung)

zwischen die Stifte quetschen:

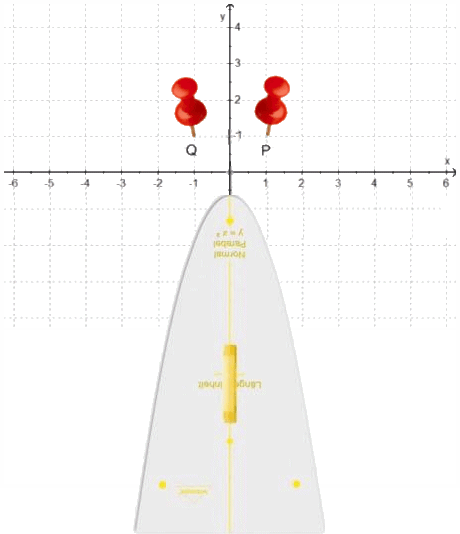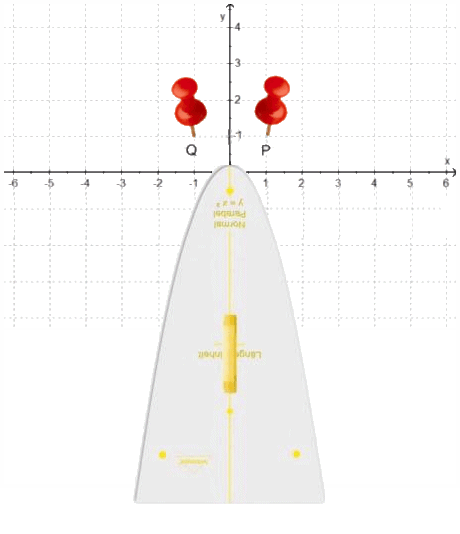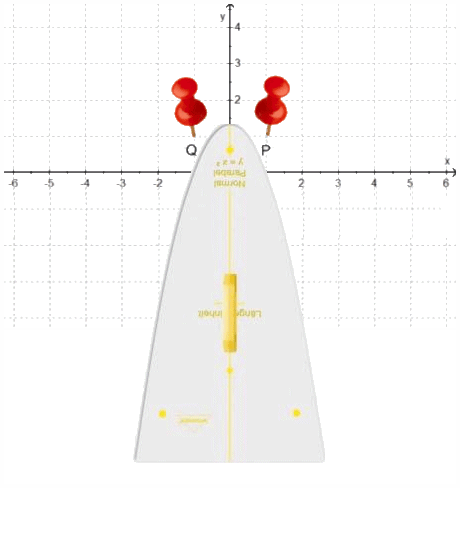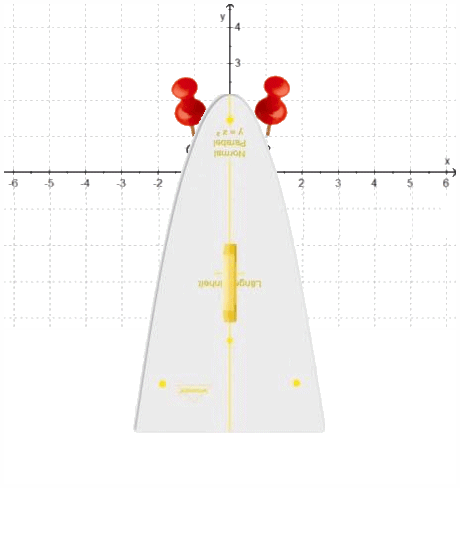
(Hier zeigt sich schon, dass ich mir Funktionsgraphen regelrecht materiell und ihr Zeichnen handwerlich vorstelle.
Nebenbei: man kann die Parabel auch schief zwischen die Stifte zwängen, sie "zentriert" sich schon von selbst, so dass ihr Scheitelpunkt oben liegt.)

Nun ergeben sich mehrere Funktionsgraphen bzw. eine Funktionenschar allerdings erst dadurch, dass nicht nur Normal-, sondern auch gestreckte und gestauchte Parabeln möglich sind, also z.B.

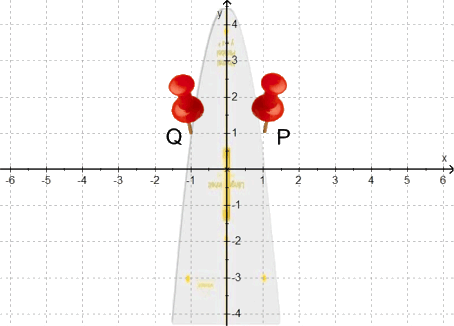   oder 

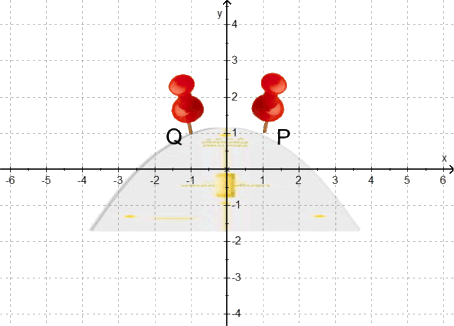
Wenn wir uns nun all diese möglichen Parabeln hübsch nacheinander vorstellen, ergibt sich folgende Bewegung:

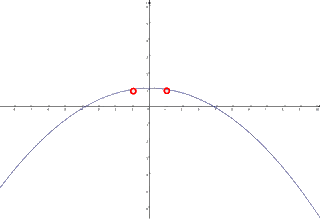
Daran sind nun (wie so oft) vor allem die beiden Extreme interessant, nämlich

1.   wenn die Parabeln extrem gestaucht bzw. flach werden:

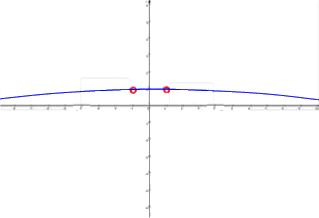
Offensichtlich nähern sich da die Flächen unter den Parabeln immer mehr der hellgrün umrandeten Fläche, also einer unendlich großen (breiten) Fläche afläche n, und somit werden hier die Flächen unter den Parabeln unendlich groß:

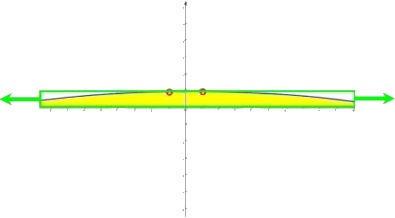
2.    wenn die Parabeln extrem gestreckt bzw. hoch werden:

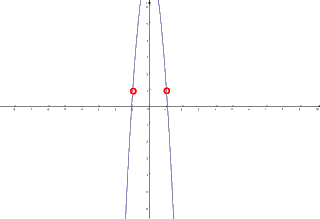
Offensichtlich nähern sich da die Flächen unter den Parabeln immer mehr der hellgrün umrandeten Fläche, also einer unendlich großen (breiten) Fläche an, und somit werden auch hier die Flächen unter den Parabeln unendlich groß:

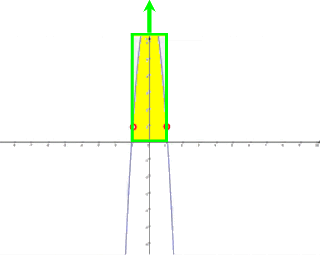
(Allemal interessant ist nebenbei auch die Gesamtfläche, die alle Flächen unter den Parabeln zusammen einnehmen bzw. die von diesen Einzelflächen nacheinander überstrichen wird, nämlich

,

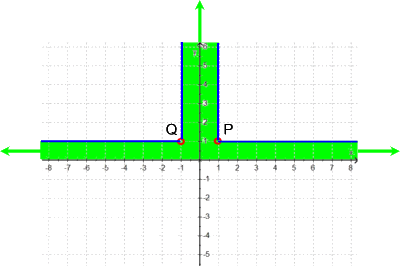wobei

• die Punkte P und Q durchaus Elemente dieser Gesamtfläche sind, da ja alle Parabeln durch diese Punkte gehen,

• während die blauen Halbgeraden nicht zu der Gesamtfläche gehören, da sie durch die Parabeln nur beliebig nah angenähert werden.)

3.    Irgendwo "in der Mitte" ergeben sich aber relativ kleine Flächen, nämlich z.B.

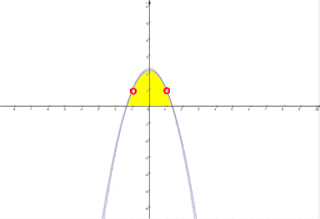
Die hier eingezeichnete, nur nach "Augenmaß" ausgewählte Fläche ist nun allerdings nicht notwendig die überhaupt kleinstmögliche. Dennoch lässt sich aber schließen:

da a in der Gleichung y = - ax² + b aus den reellen, also "dicht liegenden" (positiven) Zahlen stammt, kann man mit diesem a

• die Parabeln und mit ihnen

• die Flächen unter ihnen

kontinuierliche (stetig) ändern, und daraus folgt:

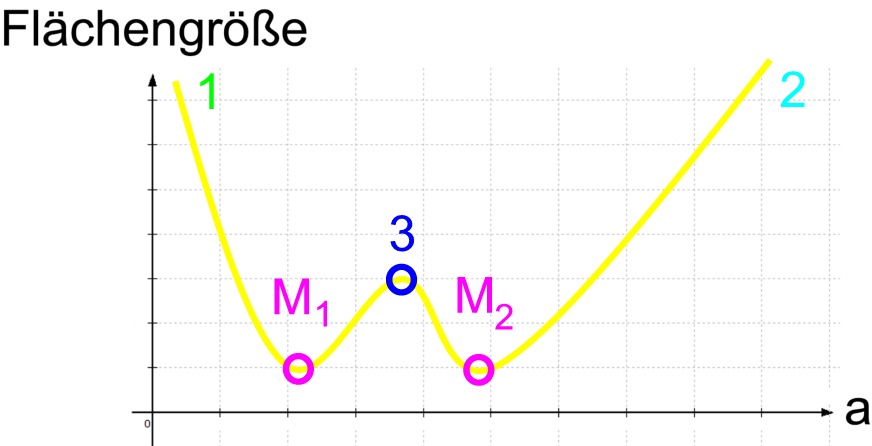
Zwischen den beiden Extremfällen 1 und 2 muss also irgendwo mindestens ein absolutes  Minimum bzw. können auch mehrere absolute Minima (z.B. M₁ und M₂) liegen, wobei allerdings nicht unbedingt bei 3 das Minimum vorliegt

.. .womit geklärt ist, welche Art Extremum in der 2. Aufgabenversion vorliegt

(und wonach wir dann auch rechnerisch suchen müssen).

Dass es in Wirklichkeit nur ein absolutes Flächenminimum gibt und wo genau es liegt, kann jedoch nur rechnerisch herausgefunden werden - was hier aber nicht ausgeführt sei.

Vielmehr geht es mir hier ja um das "Funktionen-Sehen" bzw. die Anschaulichkeit

(fernab jeder Anwendung).

Bei der Bewegung stellt sich bei mir nämlich

(und gerade das scheint mir so wichtig und hilfreich!)

unwillkürlich eine reale Vorstellung bzw. ein Bild bzw. eine Metapher ein, nämlich die bzw. das eines offenen Kamins oder einer Dunstabzugshaube, die die Funktionenschar in sich hinein schlürft:

Und wenn wir die Funktionenschar mal spaßeshalber an der x-Achse spiegeln

(wenn es in der Aufgabe also hieße, gesucht seien zur y-Achse symmetrischen, nach oben geöffnete Parabeln durch den Punkt P' ( 1 | - 1 )),

so denke ich an

Wasserstrudel

oder ein Klo, das - vornehm gesagt - Ausscheidungen runterwürgt:

Ich stelle mir die Funktionenscharen also dreidimensional vor, d.h. ich mache sie mir materiell und damit be-greifbar.

Wenn mir zu den jeweiligen Funktionenscharen jeweils mehrere Metaphern einfallen, wird deutlich, dass es keine 1:1-Bezeihung zwischen einem mathematischen Sachverhalt und einer Metapher gibt. Und zudem sind die Metaphern meistens subjektiv, d.h. der eine denkt bepielsweise an einen Strudel, der andere hingegen an ein Klo

(es scheint allerdings auch "objektive" Metaphern zu geben; so denken beispielsweise bei einem Zylindern mit oben und unten angesetzten Halbkugeln viele Menschen automatisch an , was allerdings sicherlich nicht daran liegt, dass ein Archetyp ist, sondern daran, dass der bewusste geometrische Körper im Alltag anscheinend nur in dieser Form vorkommt - womit sich andeutet, dass es für einige mathematische Sachverhalte [z.B. die oben genannte Ableitungseigenschaft der e-Funktion] vielleicht gar keine alltägliche Vorstellungen [Metaphern] gibt und diese Sachverhalte deshalb wohl abstrakt bleiben müssen).

Ich bin mir sicher, dass

• das Genie vieler großer Mathematiker gerade darin bestand bzw. besteht, mathematische Sachverhalte andauernd mit alltäglichen Metaphern zu verbinden, also erstaunlich anschauliche Mathematik zu betreiben,

• viele SchülerInnen aber keinerlei Metaphern zur Verfügung haben.

Das erinnert daran, was ich für mein zweites Fach, nämlich Deutsch, behaupte:

• dass Literatur nur lebendig machen kann, wer sie mit vielfältigen eigenen Erfahrungen auffüllen / analog setzen / kontrastieren kann,

• dass jugendliche SchülerInnen aber diese vielfältigen Vorerfahrungen naturgemäß noch gar nicht haben (können)

(es mag paradox erscheinen, aber Genies können im Gegensatz zu vielen SchülerInneN noch einfach denken bzw. sich die mathematischen Sacherhalte einfach machen!).

Und doch gibt es einen gewaltigen Unterschied zwischen Deutsch und Mathematik:

• es mag noch nicht jeder z.B. tragische Irrwege seines Lebens (für ein Gedicht mit eben diesem Thema) erkannt haben,

• aber jeder (auch Jugendliche!) hat doch wohl mal einen Kamin / eine Dunstabzugshaube / einen Wasserstrudel / ein Klo gesehen!?

Fragt sich nur, ob jeder die gegenständliche Welt wirklich (sozusagen aneignend) mit offenen Augen gesehen oder nur als allzu selbstverständlich

(weil immer mehr perfekt fertig)

 hingenommen hat.

Und vielleicht finden die SchülerInnen nur deshalb keine alltäglichen Metaphern, weil

• Mathematik im Unterricht immer als per se abstrakt verkauft und

• das Parallelisieren mit alltäglichen Dingen/Vorgängen nie geübt wurde.

Wie schon angedeutet, hat all das jedoch nichts mit der Anwendung von Mathematik zu tun:

•     bei Anwendungen beschreiben z.B. Funktionsscharen nur (!) außermathematische Sachverhalte

(welche parabelförmige Geschossbahn führt ins Ziel?),

    aber die Mathematik und der außermathematische Sachverhalt bleiben einander "wesensfremd",

Hier ist also

• (noch) nicht ein "mathematischer Blick" auf die alltägliche Wirklichkeit gemeint

(also ein vielleicht doch arg verengter Blick, der allüberall Anwendungsmöglichkeiten der Mathematik erkennt),

• sondern (nur), dass die (noch) völlig unmathematisierte Wirklichkeit als gigantisches Metaphernreservoire für innermathematische Sachverhalte ausgeschlachtet wird.

Um es an einem mechanischen Beispiel zu verdeutlichen:

• da wird nicht versucht, ein Auto (u.a. mittels Mathematik) zu verstehen

(das dürfte viele SchülerInnen auch wohl wenig interessieren; und doch wäre  ein durchaus mal interessantes Unterrichtsthema),

• sondern das Auto dient "nur" als Metaphernhalde für die Mathematik

(beispielsweise die Scheibenwischer als [begrenztes] Modell für die Scherung oder die Kombination Kurbelwelle/Pleuelstangen/Zylinder als [begrenztes] Modell für den Sinus).

Wenn man also mit den SchülerInneN zusammen einen Schrottwagen komplett auseinandernähme und ihn dann wieder (ohne Karosserie) feinsäuberliche wieder zusammensetzen würde 

  ,

wäre das ein höchst wichtiger, wenn auch indirekter Beitrag zu einem besseren Verständnis - wohl auch des Autos, hier aber doch vor allem der Mathematik

(man müsste als LehrerIn viel mehr Freiheiten für derart nicht [immer quantitativ] Abprüfbares haben).