

![]() 1. viel Theorie
1. viel Theorie
![]() 2. schnelle Praxis
2. schnelle Praxis
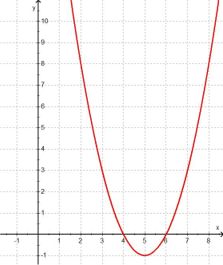
Nehmen wir als Einstieg die beiden sehr einfachen quadratischen Funktionen
f:
y = x2 - 4x +
3
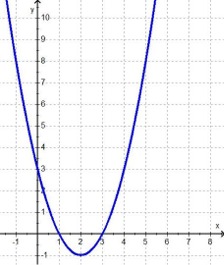
g:
y = x2 - 10x + 24
Nun sei eine dritte Funktion h definiert als Quotient der beiden Funktionen f und g, also
![]() ,
,
womit sich ergibt:
![]() .
.
Da
solche Quotientenfunktionen Brüche aus zwei anderen Funktionen (f und g) sind
und Brüche auch als "rationale Zahlen" bezeichnet werden
(wobei lat. ratio hier "Verhältnis" bedeutet),
werden solche Quotientenfunktionen auch (in einem ersten Schritt) "rationale Funktionen" genannt.
Nun gilt aber:
so, wie man jede ganze Zahl auch als Bruch darstellen kann
(also z.B. ![]() ;
womit die ganzen Zahlen eine Teilmenge
der Brüche sind),
;
womit die ganzen Zahlen eine Teilmenge
der Brüche sind),
so lässt sich beispielsweise auch die Funktion f: y = x2 - 4x + 3 als rationale Funktion darstellen:
f: y =
![]()
Und so nennt man dann auch
nachträglich Funktionen der Art f: y = x2 - 4x + 3
(oder allgemein: f: y = anxn + an-1xn-1 + ... + a2x2 + a1x1 + a0)
"ganzrationale Funktionen"
und
(in Analogie zu "echten" Brüchen )
"echte" Quotientenfunktionen
(die nicht so kürzbar sind, dass der Nenner 1 wird)
"gebrochen rationale Funktionen"
(was letztlich doppelt gemoppelt ist).
 |
Bereits hier sei eine weitere Ähnlichkeit zwischen Brüchen und gebrochen rationalen Funktionen eingeschoben:
(und das lasse man sich als "Rache des kleinen Mannes" genüsslich auf der Zunge zergehen!) auch die besten MathematikerInnen nicht mal (direkt) mit Brüchen rechnen können (z.B. sondern solch eine Rechnung mit Bruchrechengesetzen auf das Rechnen mit ganzen Zahlen zurückführen müssen (z.B.
(also
(direkt) abzuleiten, sondern man muss ihre Ableitung auf die (glücklicherweise sehr einfachen) Ableitungen der beiden ganzrationalen Funktionen f und g zurückführen, aus denen diese gebrochen rationalen Funktionen zusammengesetzt sind. Wie das geht (nämlich mit der sogenannten "Quotientenregel"), sei weiter unten erklärt. |
 |
Wenn man nun wissen will,
wie die Funktion
![]() (genauer: ihr Funktionsgraph) aussieht,
(genauer: ihr Funktionsgraph) aussieht,
d.h. wie die Funktion sich für verschiedene x-Werte verhält,
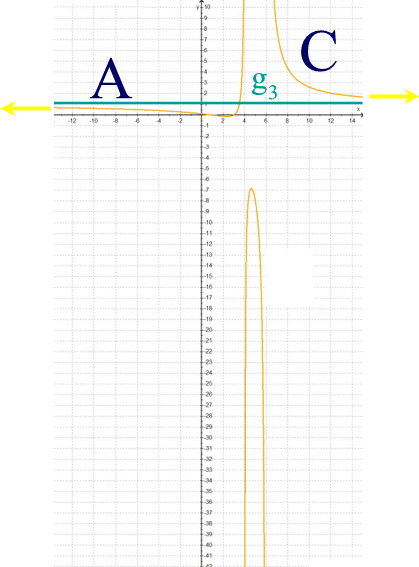
liegt es natürlich nahe, sie in einen Funktionenplotter oder auch einen G(rafischen)T(aschen)R(echner) einzugeben, womit man dann erhält:
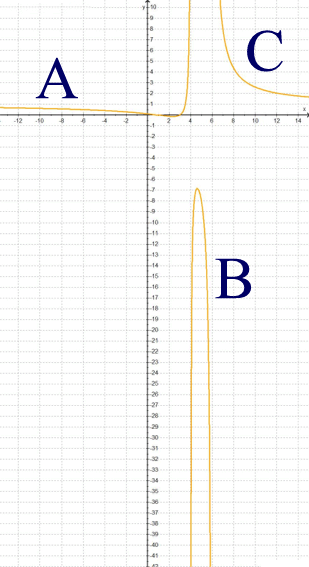
Daran ist doch
(im Vergleich mit bislang durchgenommenen, meist ganzrationalen Funktionen)
immerhin schon mal bemerkenswert, dass der (Gesamt-)Graph von h
nicht mehr zusammenhängt
bzw. nicht mit einem durchgehenden Strich zeichenbar,
also nicht "stetig" ist,
sondern aus den drei getrennten "Zweigen" A, B und C besteht.
Zudem vermutet man vielleicht
(mit allerdings schon geübtem Blick)
auch schon zwei andere merkwürdige Eigenschaften:
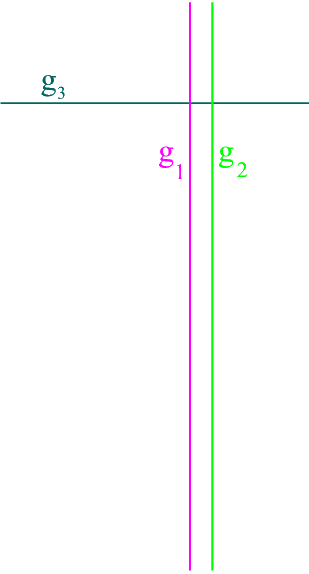
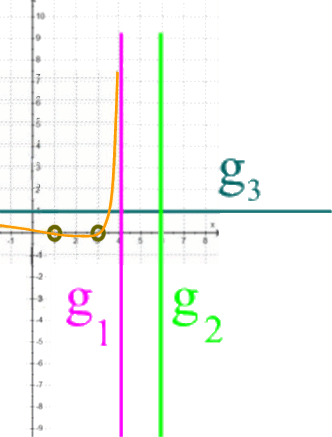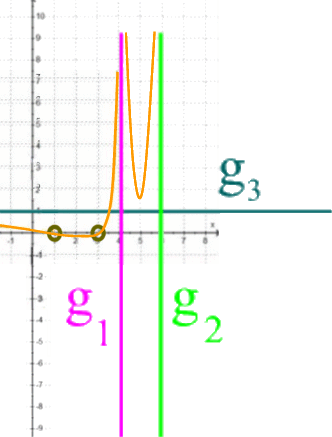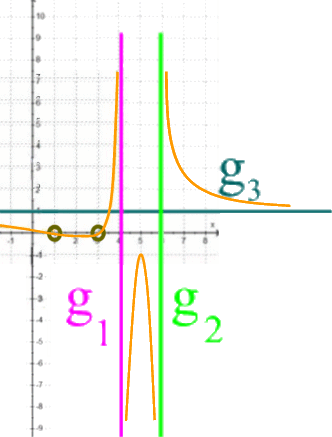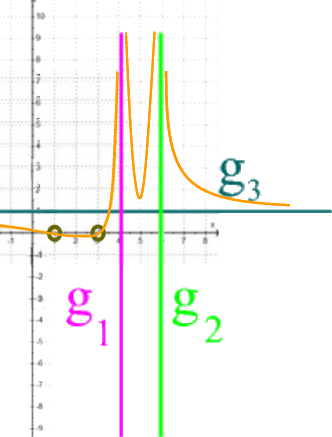
, dass die steil ansteigenden bzw. fallenden Graphenteile D, E, F und G gegen die beiden Geraden g1 und g2 zu gehen scheinen:
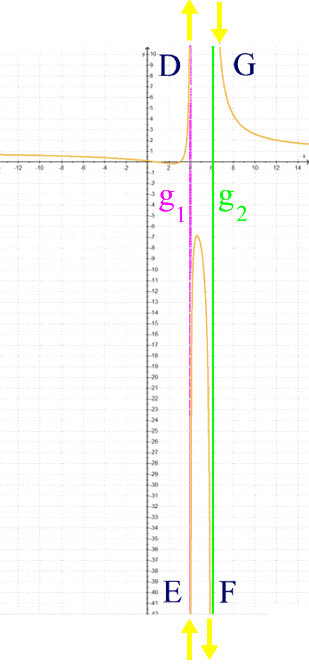
, dass die Zweige A und C für sehr große positive bzw. negative x gegen die Gerade g3: y = 1 zu gehen scheinen:
... womit wir insgesamt folgendes Gerüst erhalten würden, in das die Funktion h hineingequetscht wäre:
Standardmäßig interessiert man sich bei Funktionen auch noch für die besonders aussagekräftigen und leicht zu berechnenden Nullstellen, also für ihre Schnittpunkte mit der x-Achse. Um diese bei der Funktion h überhaupt erkennen zu können, müssen wir uns aber einen vergrößerten Ausschnitt der bisherigen Zeichnungen anschauen:

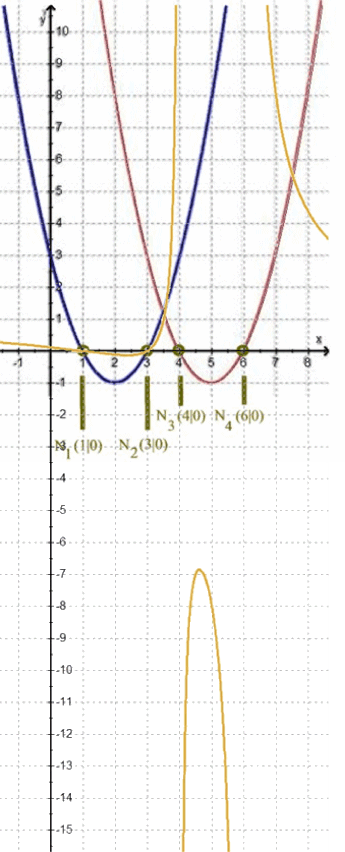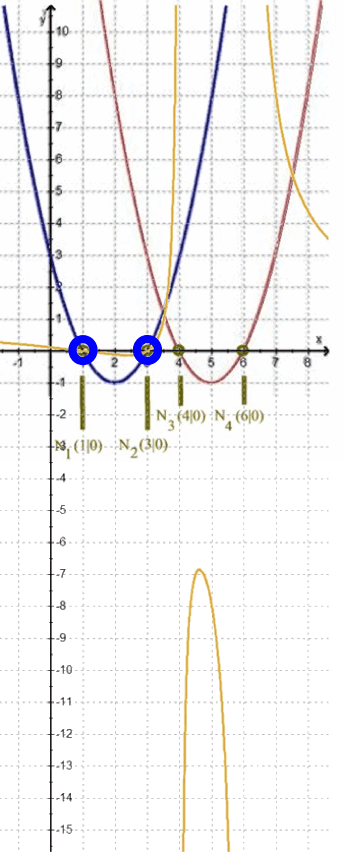
Es scheint also, dass die Funktion h so ungefähr die Nullstellen N1 ( 1 | 0) und N2 (3 | 0 ) hat.
All das sind aber bisher nur Vermutungen, und schon gar nicht wird klar, warum das alles so ist
(wenn es denn überhaupt so ist).
 |
Hier (das sei kurz eingeschoben) sieht man sehr deutlich die Vor- und Nachteile von (Computer-)Funktionenplottern und G(rafischen)T(aschen)R(echnern):
(und dennoch erkennt sie/er - wie wir unten noch sehen werden - schon anhand der Funktionsgleichung einige grundsätzliche Merkmale des Funktionsgraphen);
(und ohne geschultes Auge werden einem so einige seiner Eigenheiten auch kaum auffallen), und wieso sollte man das überhaupt noch genauer untersuchen, wo doch "alles" schon fertig ist (zu sein scheint)? Kommt hinzu, dass einige der oben vermuteten Eigenschaften des Funktionsgraphen bei einem vom Computer vorgegebenem ungünstigen Ausschnitt nur schwer oder gar nicht erkennbar sind (z.B. die Gerade g3
in Vorsicht: da Computerprogramme naturgemäß nicht mit unendlich großen Zahlen rechnen können, schneiden sie den Funktionsgraphen oben und unten einfach ab. Und einige Programme sind wohl auf Stetigkeit programmiert, d.h. sie verbinden fälschlich die obersten und untersten Punkte:
|
|
 |
Oben hatten wir anhand des Graphen von h nur vermuten können, dass er ungefähr die Nullstellen N1 ( 1 | 0) und N2 (3 | 0 ) hat. Nun sorgen wir dafür, dass er exakt dort seine Nullstellen hat. Dazu definieren wir uns
eine quadratische Funktion j mit Nullstellen bei x = 1 und x = 3
und eine weitere quadratische Funktion k mit Nullstellen bei x = 4 und x = 6.
Zu a.: x = 1 oder x = 3
| -1 | - 3
![]() x -
1 = 0
oder x - 3
= 0
x -
1 = 0
oder x - 3
= 0
![]() (x - 1)
•
(x - 3) = 0
(x - 1)
•
(x - 3) = 0
Die zugehörige quadratische Funktion j ist dann
j: y = (x - 1) • (x - 3)
Hier ist die Funktion j in der sogenannten "Nullstellenform" gegeben. Üblicherweise wird SchülerInnen aber die sogenannte "Standardform" gegeben, in die wir nun durch Auflösen der Klammern umformen:
j: y = (x - 1) • (x - 3) = x2 - 4x + 3
Damit ist aber klar, dass unsere neue Funktion j
(welch Wunder!)
mit der oben genannten Funktion f identisch ist, weshalb wir im Folgenden nur noch von f sprechen
(in Wirklichkeit habe ich natürlich erst die Nullstellenform (x - 1) • (x - 3) gehabt und daraus danach die Standardform x2 - 4x + 3 hergeleitet).
Zu b.: x = 4 oder x = 6
| -4 | - 6
![]() x -
4 = 0
oder x - 6
= 0
x -
4 = 0
oder x - 6
= 0
![]() (x - 4)
•
(x - 6) = 0
(x - 4)
•
(x - 6) = 0
Die zugehörige quadratische Funktion k ist dann
k: y = (x - 4) • (x - 6)
Die Funktion k ist hier in der "Nullstellenform" gegeben. Wir überführen sie wieder durch Auflösen der Klammern in die "Standardform" :
k: y = (x - 4) • (x - 6) = x2 - 10x + 24
Damit ist aber klar, dass unsere neue Funktion k mit der oben genannten Funktion g identisch ist, weshalb wir im Folgenden nur noch von g sprechen.
 |
Ich habe für die Funktionen f und g bewusst einfache, also
genommen, nämlich 1, 3, 4 und 6. Da stellt sich doch die Frage, ob's nicht noch einfacher ginge, nämlich mit den hübsch benachbarten Nullstellen 1, 2, 3 und 4 . Ich habe aber die Nullstellen der Einzelfunktionen bewusst so gewählt, dass sie einen Abstand von 2 haben. Weil nämlich Normalparabeln vorliegen, lassen sie sich dann besonders einfach zeichnen:
|
 |
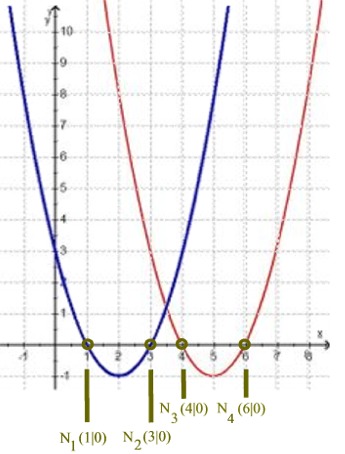
Zeichnen wir nun die beiden Funktionsgraphen von f und g in ein einziges (leicht vergrößertes) Koordinatensystem:
Und nun sei auch noch der Graph der Quotientenfunktion h in dasselbe Koordinatensystem eingezeichnet:
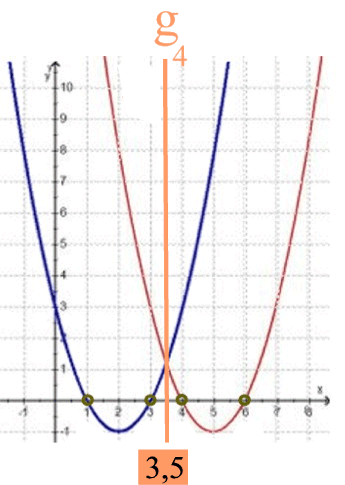
Daran könnte nun auffallen, dass
die Quotientenfunktion h dieselben Nullstellen N1 ( 1 | 0) und N2 (3 | 0 ) zu haben scheint wie die Funkion f im Zähler:
die Quotientenfunktion h genau dort gegen die Geraden g1 und g2 zu laufen scheint, wo die Funktion g aus dem Nenner ihre Nullstellen N3 ( 4 | 0) und N4 (6 | 0 ) hat:
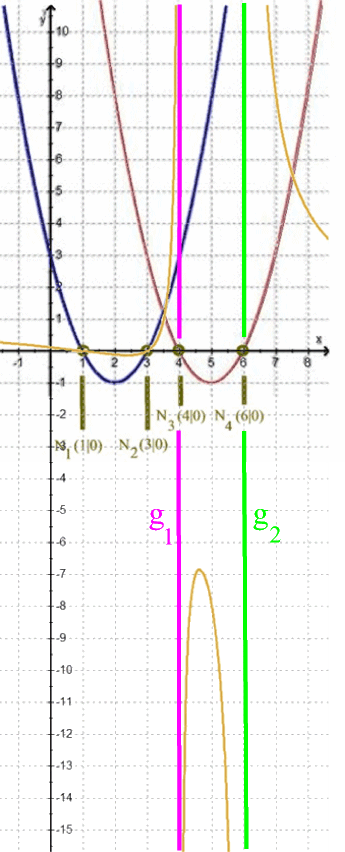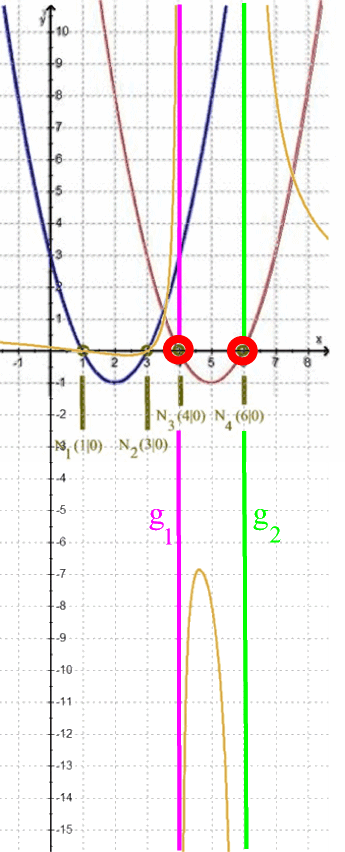
Hier lässt sich schon mal feststellen:
| wenn 1. und 2. zutreffen, dann haben die Nullstellen
von f und g
eine sehr große Bedeutung für
|
Schauen wir uns aber zuerst mal an, ob 1. und 2. wirklich zutreffen - und wenn ja: weshalb?
Da müssen wir nicht mal viel Ahnung von Quotientenfunktionen haben, sondern es reicht die Kenntnis einfacher Brüche :
Zu 1.:
ein Bruch
![]() ist
genau dann gleich Null, wenn sein
Zähler f Null
ist
ist
genau dann gleich Null, wenn sein
Zähler f Null
ist
(es kriegt nur dann keiner was zu essen, wenn gar kein Essen verteilt wird).
Zu 2.:
wenn in einem Bruch
![]() der
Nenner g gleich Null
ist, wenn also durch Null
dividiert wird, geschieht der mathematische Super-GAU (größte
anzunehmender Unfall)
der
Nenner g gleich Null
ist, wenn also durch Null
dividiert wird, geschieht der mathematische Super-GAU (größte
anzunehmender Unfall)
 .
.
Diesem Super-GAU muss dringend dadurch zuvorgekommen werden, dass die Nullstellen des Nenners g
• gleich zu Anfang nicht zum Rechnen zugelassen werden,
• dass sie also sofort rabiat aus dem
![]() efinitionsbereich
von h verbannt werden:
efinitionsbereich
von h verbannt werden:
![]() =
=
![]() \ {
4 ; 6
}
\ {
4 ; 6
}
(d.h. der
![]() efinitionsbereich
von h enthält sämtliche [unendlich viele]
reellen Zahlen -
efinitionsbereich
von h enthält sämtliche [unendlich viele]
reellen Zahlen -
außer den beiden Nullstellen
4 und 6
der Funktion g im Nenner).
"zuvorkommen", "gleich zu Anfang" und "sofort" bedeuten aber:
|
Da unsere Funktion
![]() die beiden
die beiden
![]() efinitionsbereichs-Lücken
4 und 6
hat, kann sie nicht mehr "stetig", d.h. mit einem einzigen
durchgehenden Strich zeichenbar sein
efinitionsbereichs-Lücken
4 und 6
hat, kann sie nicht mehr "stetig", d.h. mit einem einzigen
durchgehenden Strich zeichenbar sein
(bei 4 und 6 müssen wir den Stift für kurze Zeit vom Blatt abheben; wir werden unten noch sehen, dass das manchmal zeichnerisch gar nicht möglich ist).
Das aber bedeutet, dass der Funktionsgraph in die drei Einzel"zweige" A, B und C zerfällt:

Innerhalb dieser Einzel"zweige" ist die Funktion h aber durchaus "stetig", d.h. jeder Einzel"zweig" ist mit einem einzigen durchgehenen Strich zeichenbar. Man sagt deshalb auch, dass
(auf
ganz
![]() )
)
stetig ist,
(innerhalb
der Zweige bzw. der übrigbleibenden
![]() efinitionsbereichs-Teile)
efinitionsbereichs-Teile)
stetig ist.
Wir wissen inzwischen also,
 passieren, nämlich - igitt! - durch Null
geteilt würde
passieren, nämlich - igitt! - durch Null
geteilt würde(weshalb wir - so leichthin schließen
Mathematiker das Grauen aus - diese x-Werte ja eben von Anfang an gar im nicht
![]() efinitionsbereich zulassen),
efinitionsbereich zulassen),
Das sei durch möglichst anschauliche, wenn auch mathematisch "unsaubere" Überlegungen ermittelt
(ich bin mir ja zwecks Anschaulichkeit zu nix zu schade!):
es ergibt sich
![]()
(...wobei "sehr klein" vorliegt, da wir ja x ganz nah an einer Nullstelle von g gewählt haben):
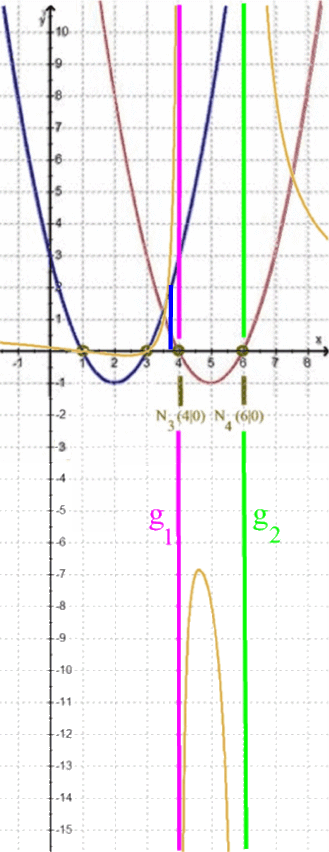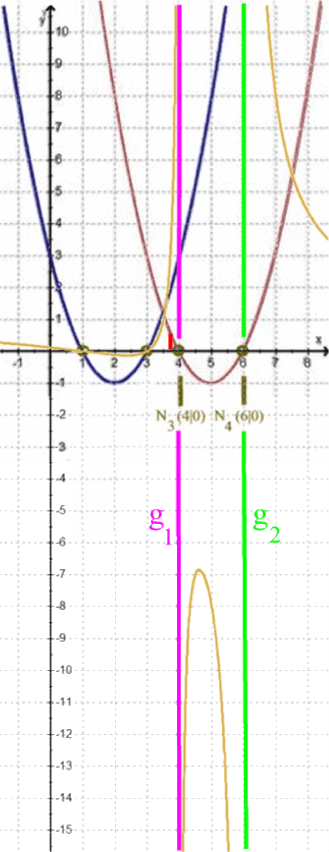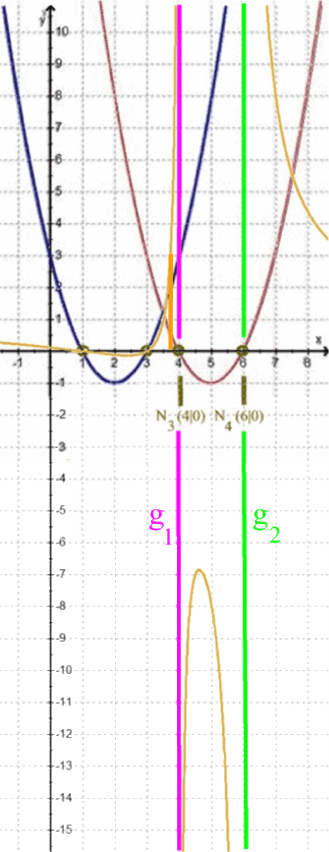
Je näher nun x von links an 4 heran rutscht, desto größer wird h(x), so dass der Zweig ganz nah bei g1 unendlich hoch wird, aber
Man sagt auch: h läuft von links "asymptotisch" gegen g1 .
Der Graph von h ist ganz knapp links von g1 eine permanente Linkskurve - was allerdings nur schwer zu zeichnen ist.
es ergibt sich
![]() :
:
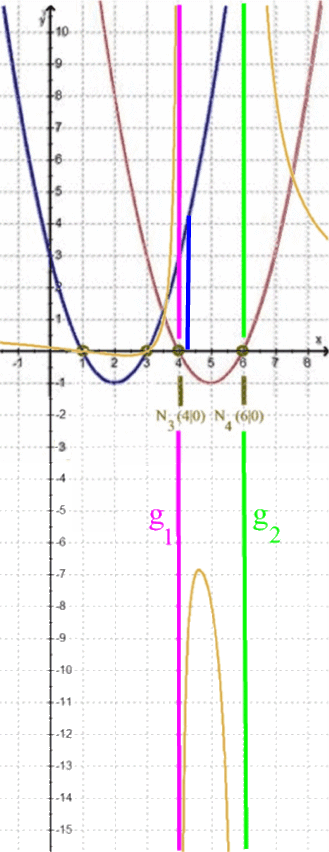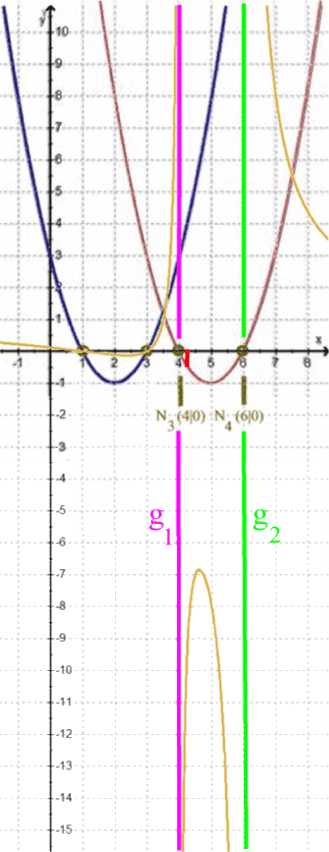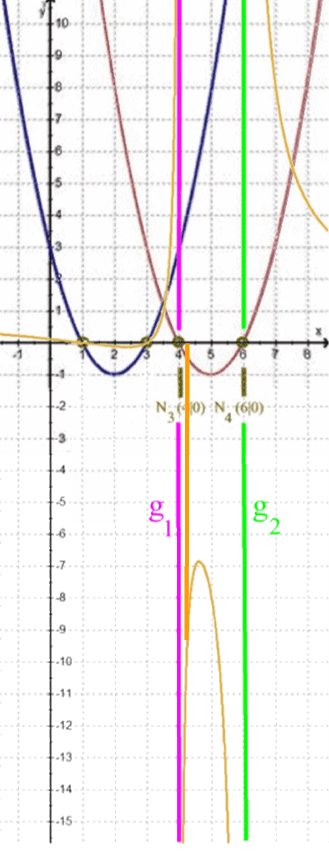
Je näher nun x von rechts an 4 heran rutscht, desto weiter geht h nach unten.
es ergibt sich
![]() :
:
Je näher nun x von links an 6 heran rutscht, desto weiter geht h nach unten.
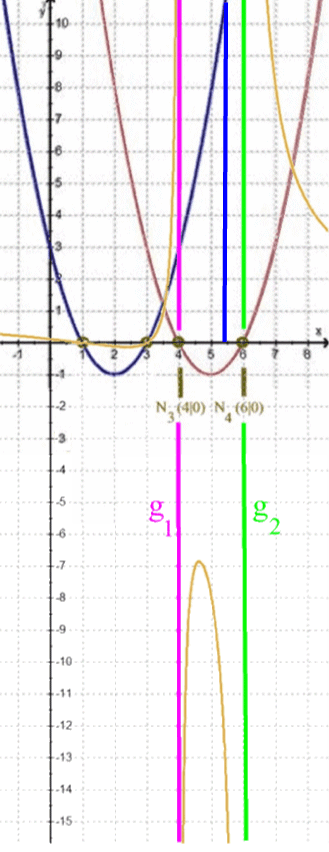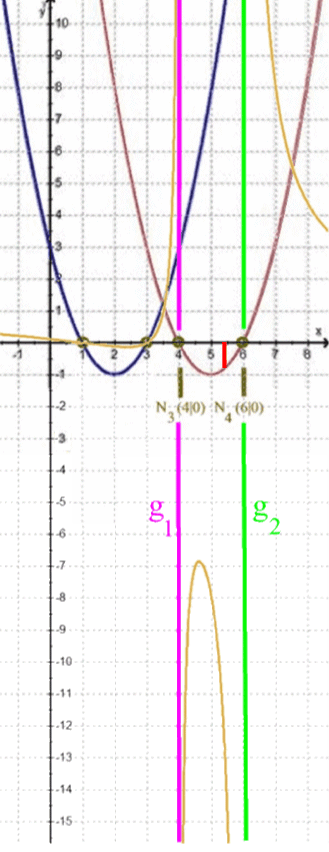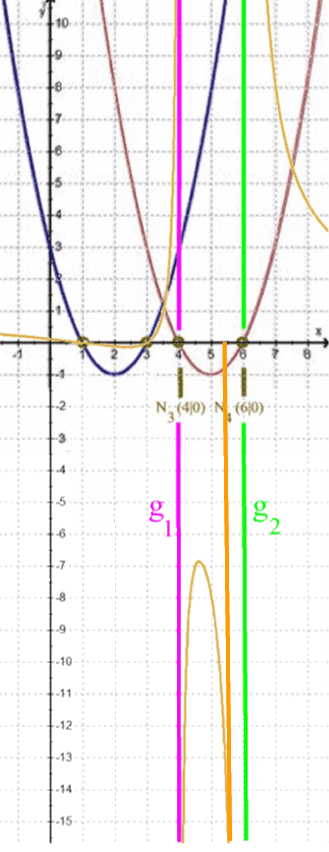
es ergibt sich
![]() :
:
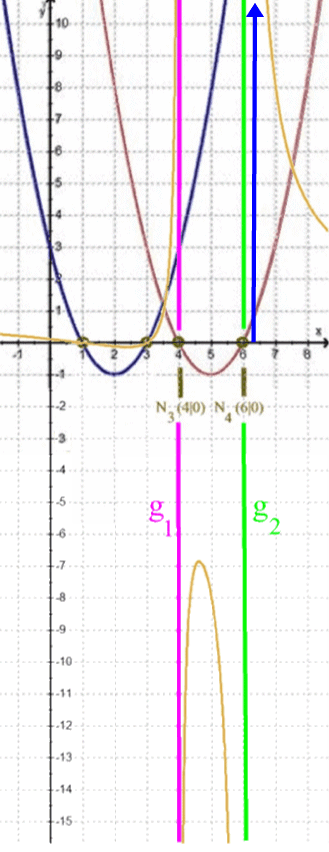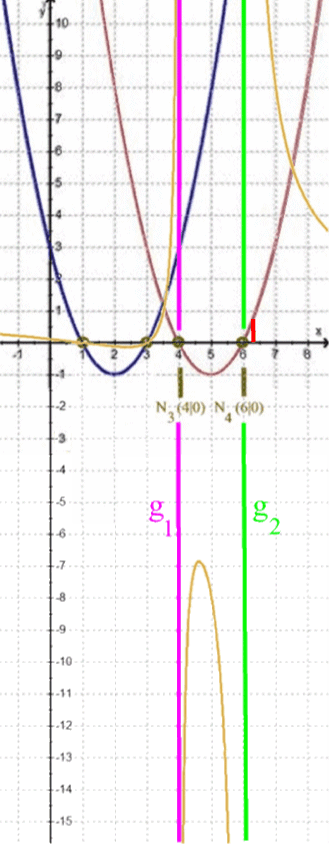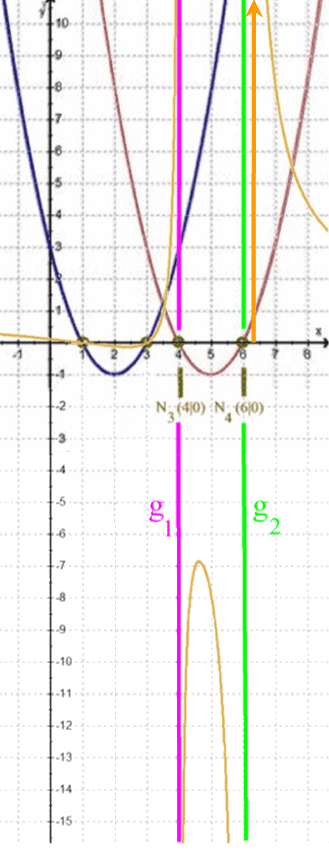
Je näher nun x von rechts an 6 heran rutscht, desto weiter geht h nach oben.
Nun bleibt vorerst nur noch zu klären, weshalb die Zweige A und C der Quotientenfunktion h für sehr große positive bzw. negative x (angeblich) gegen die Gerade g3: y = 1 gehen:

Schauen wir uns dazu zuerst die Einzelfunktionen f: y = x2 - 4x + 3 und g: y = x2 - 10x + 24 an: beide sind quadratische Funktionen, deren quadratischer Summand x2 für sehr große positive oder negative x sehr viel mehr ins Gewicht fällt als die Restterme - 4x + 3 bzw. - 10x + 24.
Für sehr große positive oder negative x können wir also sagen:
f: y = x2 - 4x + 3 ≈ x2 ,
g: y = x2 - 10x + 24 ≈ x2 .
Und daraus folgt im Hinblick auf h für sehr große positive oder negative x :
![]() ≈
≈
![]() = 1
.
= 1
.
Damit haben wir insgesamt das bereits oben erwähnte Gerüst
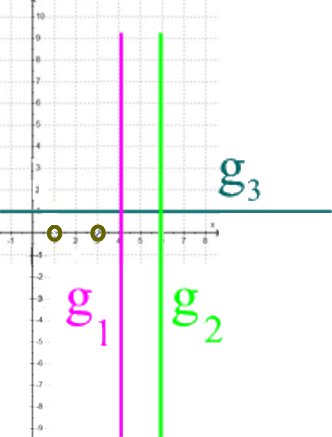 ,
,
in das der Funktionsgraph von h nur noch etwa so reinpasst:
 |
Damit kurz zurück zu "und dennoch erkennt [einE MathematikerIn] [...] schon anhand der Funktionsgleichung einige grundsätzliche Merkmale des Funktionsgraphen": ohne großartige Rechnungen haben wir dennoch mittels des "Gerüsts" den ungefähren Verlauf des Funktionsgraphen von h "vorhersagen" können. Solches Vorauswissen ist aber wichtig, um es später mit den Rechenergebnissen vergleichen zu können, also
|
 |
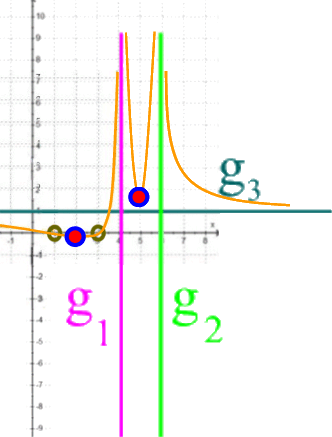
Anhand unserer "Gerüst"-Vorüberlegungen können wir schon zwei
Extrema
![]() (Minima bzw. Maxima) erahnen:
(Minima bzw. Maxima) erahnen:
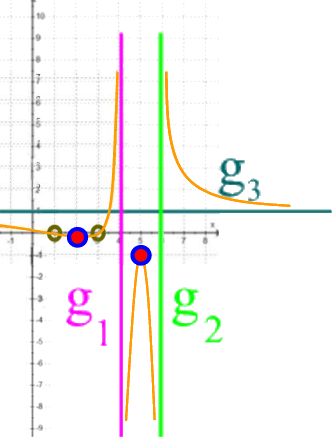
oder
Und diese Extrema sind erwartbar
zwischen den beiden Nullstellen 1 und 3 von f bzw. h
(exakt in der Mitte, also bei 2 ???),
zwischen den beiden Nullstellen 4 und 6 von g
(exakt in der Mitte, also bei 5 ???).
 |
Nebenbei ist auch schon (mindestens) ein
Wendepunkt
(Übergang von einer Rechts- in eine Linkskurve) erahnbar:
|
||
 |
Um aber die Extrema
![]() der Quotientenfunktion
der Quotientenfunktion
![]() bestimmen zu können, müssen wir sie
ableiten.
bestimmen zu können, müssen wir sie
ableiten.
Wie bereits oben gesagt, geht das aber überhaupt nicht direkt, sondern nur auf dem Umweg über f und g bzw. deren Ableitungen f ' und g ' .
 |
Solch einE Umweg/Umleitung ist aber in der Mathematik oftmals der
(einzig mögliche)
Königsweg:
|
Nun sei endlich die lang angekündigte "Quotientenregel " eingeführt
(allerdings ohne Herleitung und Beweis):
wenn
|
Um konkret zu werden, berechnen wir erstmal nach altbekannter und sehr einfacher Regel die Ableitungen der beiden ganzrationalen Funktionen f und g :
f: y = x2 - 4x + 3 ⇒ f ' : y = 2x - 4
g: y = x2 - 10x + 24 ⇒ g ' : y = 2x - 10
Wenn wir nun die konkreten Funktionsterme von f und g sowie f ' und g ' in die Quotienrenregel einsetzen
(und zwar - wie noch zu begründen ist - nur in den Zähler),
so ergibt sich
h ' =
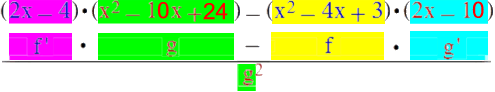
oder kürzer
h ' =
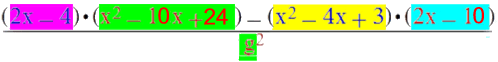 .
.
Um nun herauszufinden, wo die Funktion h potentielle Extrema hat, müssen wir die Nullstellen ihrer Ableitung h ' bestimmen. Die Frage ist also:
h ' =
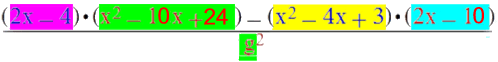 =
0
???
=
0
???
Hier hilft nun nochmals die Erkenntnis, die bereits oben nützlich war: ein Bruch ist genau dann gleich Null, wenn sein Zähler Null ist:
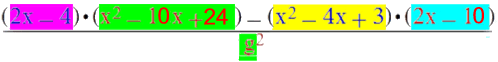 = 0
⇔
= 0
⇔
⇔
![]() =
0
.
=
0
.
Für die Ermittlung der Extrema ist also der Nenner g2 unerheblich - und deshalb mussten wir ihn auch gar nicht ausrechnen.
Der Zähler
![]() ist
nun aber nicht mehr gebrochen
rational, sondern altbekannt
ganzrational, und
mit
ganzrationalen
Funktionen können wir ja bereits prächtig umgehen.
ist
nun aber nicht mehr gebrochen
rational, sondern altbekannt
ganzrational, und
mit
ganzrationalen
Funktionen können wir ja bereits prächtig umgehen.
Um die Nullstellen
von
![]()
(d.h. die potentiellen Extrema von h)
zu finden, müssen wir nun allerdings erstmals schnöde und umständlich rechnen
(Rechnen ist keine Mathematik, sondern nur
lästiges, wenn auch unvermeidliches Handwerkszeug:
 ),
),
nämlich die Klammern beseitigen und zusammenfassen:
![]() =
=
= 2x3 - 20x2 + 48x - 4x2 + 40x - 96 - 2x3 +10x2 + 8x2 - 40x - 6x +30 =
= - 6x2 + 42x - 66 = 0 ???
Das Ergebnis - 6x2 + 42x - 66 = 0 ist nun doppelter Anlass, fröhlich zu jubilieren:
: obwohl zwischendurch mal Terme dritten Grades, nämlich die beiden 2x3 , vorkamen, heben sie sich doch hübsch passend gegenseitig auf und bleibt also nur der quadratische Term - 6x2 + 42x - 66 über; und die Nullstellen quadratischer Funktionen können wir sehr einfach berechnen, falls überhaupt Nullstellen vorliegen;
: zur Lösung von - 6x2 + 42x - 66 = 0 müssen wir erstmal normieren, also die beiden ganzen Seiten der Gleichung durch - 6 teilen; da ist es uns doch ausgesprochen willkommen, dass
(wie durch ein Wunder!)
alle drei Koeffizienten 6, 42 und 66 glatt durch 6 teilbar sind:
- 6x2 + 42x - 66 = 0 | : (- 6)
⇔ x2 - 7x + 11 = 0
Und das ist doch wahrhaft eine ziemlich einfache quadratische Gleichung, die wir nun beispielsweise mittels der p-/q-Formel behandeln können, wobei hier p = -7 und q = 11 ist:
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]()
 |
Eine endlich mal über den Standardstoff hinausgehende, hier aber unbeantwortete Frage ist, ob/wann (immer?) die beiden Glücksfälle auch bei anderen gebrochen rationalen Funktionen auftreten - was doch das Leben ungemein vereinfachen würde. |
Hier mag man nun die irrationale
![]() als
nicht mehr ganz so schön (einfach) empfinden
als
nicht mehr ganz so schön (einfach) empfinden
(obwohl doch
![]() eine
hübsch einfache Zahl, nämlich (
eine
hübsch einfache Zahl, nämlich (![]() ) 2
exakt gleich 1,25 ist; und was interessieren eineN MathematikerIn immer nur
ungefähre Dezimalzahlen [hier z.B. 1,118] ?!).
) 2
exakt gleich 1,25 ist; und was interessieren eineN MathematikerIn immer nur
ungefähre Dezimalzahlen [hier z.B. 1,118] ?!).
 |
Interessant an
(wo h gar nicht definiert ist)
|
"potentielle" Extrema deswegen, weil ihr "Extrem-Sein" ja eigentlich noch mit der zweiten Ableitung bestätigt werden müsste, wo sich dann auch entscheiden würde, dass M1 ein (lokales) Minimum und M2 ein (lokales) Maximum ist.
Da inzwischen aber das "gedankliche Prinzip" der Ableitung von Quotientenfunktionen klar ist, spare ich mir solch ekelhafte Rechnereien und damit auch
die Bestimmung (zweite Ableitung) und Bestätigung (pfui Deibel!: dritte Ableitung) des Wendepunkts
die Bestimmung der y-Werte von M1 und M2
(nur soviel: 3, 5 -
![]() bzw. 3,5
+
bzw. 3,5
+ ![]() für x
in die Funktionsgleichung von h einsetzen!).
für x
in die Funktionsgleichung von h einsetzen!).
Halten wir noch kurz fest:
3,5 -
![]() ≈
3,5 - 1,11 = 2,39, d.h. der x-Wert des Minimums M1 liegt
≈
3,5 - 1,11 = 2,39, d.h. der x-Wert des Minimums M1 liegt
tatsächlich, wie erwartet, zwischen den Nullstellen N1 ( 1 | 0) und N2 (3 | 0 ) von f bzw. h,
aber nicht, wie oben probeweise vermutet, genau in der Mitte, also bei 2.
3,5 +
![]() ≈
3,5 + 1,11 = 4,61, d.h. der x-Wert des Maximums M2 liegt
≈
3,5 + 1,11 = 4,61, d.h. der x-Wert des Maximums M2 liegt
tatsächlich, wie erwartet, zwischen den Nullstellen N3 ( 4 | 0) und N4 (6 | 0 ) von f bzw. den Definitionsbereichslücken von h,
aber nicht, wie oben probeweise vermutet, genau in der Mitte, also bei 5.
Es ist immer günstig,
wie oben vorweg viel von den behandelten Funktionen zu wissen
(s.o. die Nullstellen N1 ( 1 | 0) und N2 (3 | 0 ) von f und die Nullstellen N3 ( 4 | 0) und N4 (6 | 0 )von g),
aus bereits behandelten Beispielen
(den oben eingeführten Funktionen f, g und h)
neue zu entwickeln, und zwar derart, dass man immer nur an einem einzigen Schräubchen dreht, um die (monokausale) Ursache für markante Veränderungen im Auge zu behalten.
In diesem Sinne
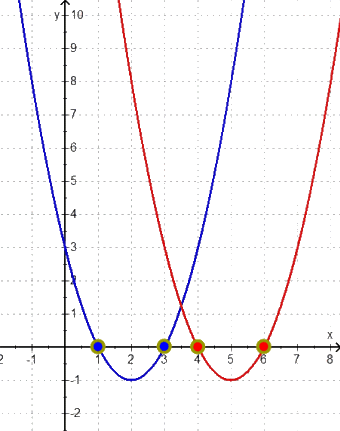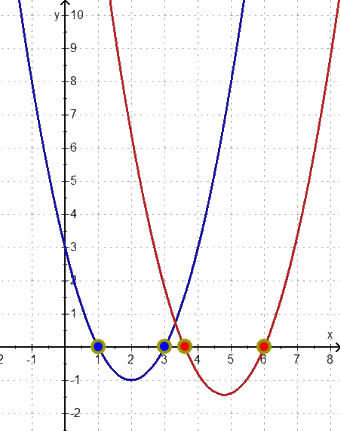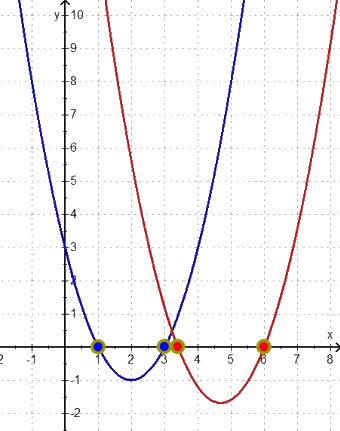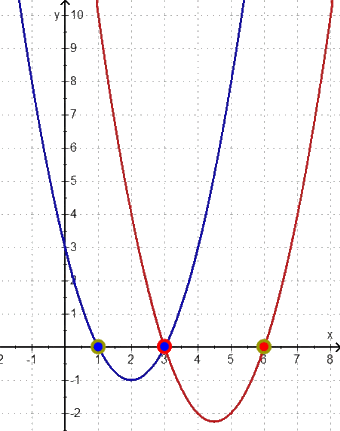
aus der Nullstellen N3 ( 4 | 0) machen wir N3 ( 3 | 0) , so dass f und g* die Nullstelle N2 (3 | 0 ) bzw. N3 ( 3 | 0) gemeinsam haben.
Damit erhalten wir als neue Funktion g*: y = (x - 3) • (x - 6) = x2 - 9x + 18 mit den Nullstellen N3 ( 3 | 0) und N4 (6 | 0 ) .
Zusammen sehen die Funktionsgraphen der unveränderten Funktion f und der neuen Funktion g* so aus:
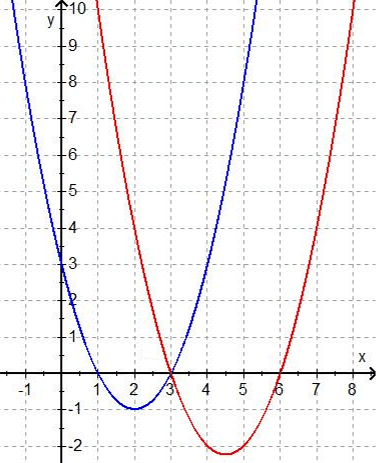
Für die neue
Quotientenfunktion h*=
![]() erhalten wir
erhalten wir
h*: y =
Den Funktionsgraph dieser neuen Quotientenfunktion h lassen wir uns bewusst noch nicht von einem Computerprogramm anzeigen, sondern stellen erstmal eigene Überlegungen an.
Wie schon oben gefordert, stellen wir zu allererst
Überlegungen zum
![]() efinitionsbereich
der neuen Quotientenfunktion
h an: da die neue Nenner-Funktion
g* die
Nullstellen
x3
= 3 und x4
= 6 hat, müssen wir diese beiden Zahlen
schleunigst aus dem
efinitionsbereich
der neuen Quotientenfunktion
h an: da die neue Nenner-Funktion
g* die
Nullstellen
x3
= 3 und x4
= 6 hat, müssen wir diese beiden Zahlen
schleunigst aus dem
![]() efinitionsbereich
von h* entfernen und erhalten
efinitionsbereich
von h* entfernen und erhalten
![]() =
=
![]() \ {
3 ; 6
} .
\ {
3 ; 6
} .
Nach unseren obigen Vorerfahrungen sind an den beiden Stellen x3 = 3 und x4 = 6 für h die Asymptoten g1 und g2 zu erwarten:
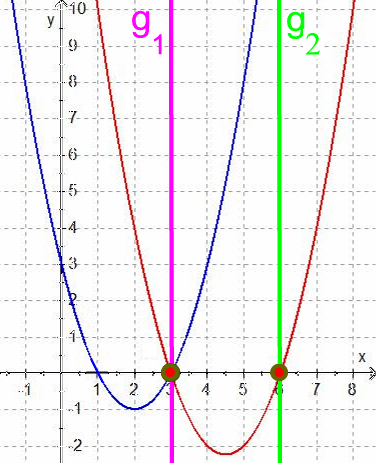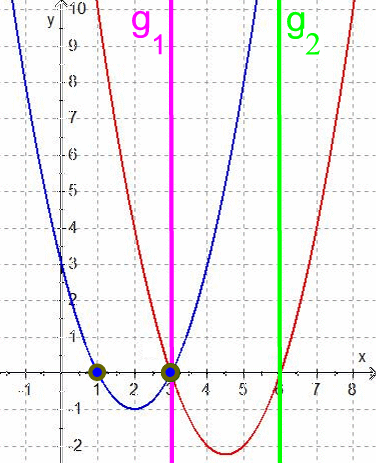
Gleichzeitig ist nach unseren obigen Vorerfahrungen zu
erwarten, dass die Quotientenfunktion
h* dieselben
Nullstellen
![]() hat wie die
Zählerfunktion f,
also N1
( 1 | 0) und N2
(3 | 0 )
.
hat wie die
Zählerfunktion f,
also N1
( 1 | 0) und N2
(3 | 0 )
.
All das zusammen würde aber bedeuten, dass die Quotientenfunktion h*
Beides gleichzeitig geht aber nicht. Womit sich ein Problem auftut, das wir aber vorerst zurückstellen.
Allemal bemerkenswert
(und unten noch wichtig)
ist, dass man alle Nullstellen von f und g* sowie die Übereinstimmung der Nullstellen N2 (3 | 0 ) und N3 ( 3 | 0)
 ablesen kann
ablesen kann
(wenn also f und g in ihren Nullstellenformen gegeben sind),
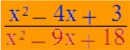
(wenn also f und g* - wie üblich - in ihren Standardformen gegeben sind).
1. macht also die Arbeit viel leichter: beim Term
 liegt es ja wohl nahe, die beiden identischen
Nullstellenklammern
(x-3) im
Zähler und (x-3)
im Nenner gegeneinander zu kürzen:
liegt es ja wohl nahe, die beiden identischen
Nullstellenklammern
(x-3) im
Zähler und (x-3)
im Nenner gegeneinander zu kürzen:
 ,
,
also insgesamt
h*: y =
 =
=
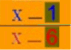
Der scheinbare Quotient zweier quadratischer Terme (links) ist also "in Wirklichkeit" nur ein Quotient zweier linearer Terme (rechts).
Es kommt sogar noch doller (einfacher): analog zu den obigen
Überlegungen zu sehr großen negativen oder
positiven x gilt nämlich, dass dort
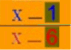 ≈
≈
 = 1.
= 1.
Insgesamt gilt also für sehr große negative oder positive x:
h*: y =
 ≈
1
≈
1
Wie oben nähert sich also auch hier der Graph der (neuen) Quotientenfunktion h der Gerade g3: y = 1 an.
Jetzt erst erlauben wir uns, ein Computerprogramm
den Funktionsgraphen der vereinfachten (neuen)
Quotientenfunktion h*:
y = 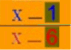 anzeigen zu lassen:
anzeigen zu lassen:
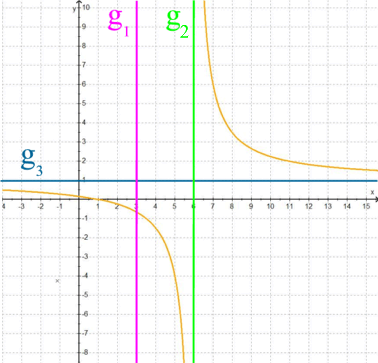
Unsere oben erarbeiteten Erwartungen sind also nur teilweise erfüllt worden:
(wie f)
in N2 (3 | 0 ) eine Nullstelle hat
(h* liegt für x = 3 ja unter der x-Achse bei y ≈ - 0,7);
Letzteres düfte uns nicht allerdings nicht allzu sehr
überraschen, hatten wir der Einfachheit halber ja 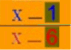 und nicht
und nicht
 in den
Computer eingegeben. Und bei h*:
y =
in den
Computer eingegeben. Und bei h*:
y = 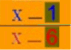 hat der Nenner ja eben für x = 3 keine
Nullstelle
(sondern nur für x = 6), so dass bei der Funktion h*:
y =
hat der Nenner ja eben für x = 3 keine
Nullstelle
(sondern nur für x = 6), so dass bei der Funktion h*:
y = 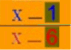 gilt:
gilt:
Das Problem ist vielmehr: wenn wir statt 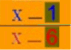 doch den schwierigeren Term
doch den schwierigeren Term
 in den
Computer eingeben, ergibt sich derselbe Funktionsgraph
in den
Computer eingeben, ergibt sich derselbe Funktionsgraph
 ,
,
scheint g1 also ebenfalls überflüssig zu sein.
Hier müssen wir uns aber an die obige Forderung
erinnern, vor jeder Rechnung den
![]() efinitionsbereich
von h*:
y =
efinitionsbereich
von h*:
y =
 zu
bestimmen, und da hier für x = 3 durchaus eine
Nullstelle des Nenners vorliegt (und auch für x =
6), gilt hier
zu
bestimmen, und da hier für x = 3 durchaus eine
Nullstelle des Nenners vorliegt (und auch für x =
6), gilt hier
![]() =
=
![]() \ {3
; 6
} !
\ {3
; 6
} !
Es war also ein bisschen leichtfertig, h*: y =
 =
=
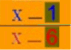 zu
schreiben:
zu
schreiben:
 und
und
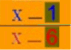 sind eben
nicht abolut identisch (=), sondern an einer einzigen
Stelle unterschiedlich, nämlich für x = 3:
sind eben
nicht abolut identisch (=), sondern an einer einzigen
Stelle unterschiedlich, nämlich für x = 3:
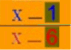 ist dort durchaus definiert,
ist dort durchaus definiert,
 ist
dort nicht definiert, was
insbesondere heißt:
ist
dort nicht definiert, was
insbesondere heißt:
 hat
dort eine punktförmige Lücke, d.h.
hat
dort eine punktförmige Lücke, d.h.
(Weil also die beiden Funktionen h*: y =
 und h**: y =
und h**: y =
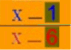 nicht
absolut exakt sind, unterscheiden wir im Folgenden zwischen
nicht
absolut exakt sind, unterscheiden wir im Folgenden zwischen

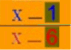 )
)
 etwas
Erstaunliches:
etwas
Erstaunliches:

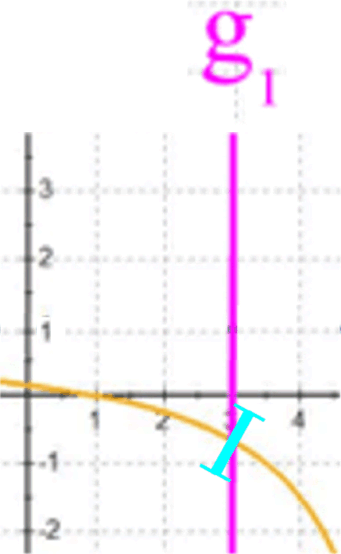

Die Funktionsgraphen von h**:
y = 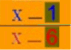 und h*: y =
und h*: y =
 sehen
also gleich aus - bis eben auf die
sehen
also gleich aus - bis eben auf die
![]() efinitionslücke
von h*: y =
efinitionslücke
von h*: y =
 in x =
3. Man kann also die
in x =
3. Man kann also die
![]() efinitionslücke
x = 3 von h*: y =
efinitionslücke
x = 3 von h*: y =
 flicken, indem man den Funktionsgraphen von h**:
y =
flicken, indem man den Funktionsgraphen von h**:
y = 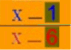 als Pflaster drüberklebt:
als Pflaster drüberklebt:
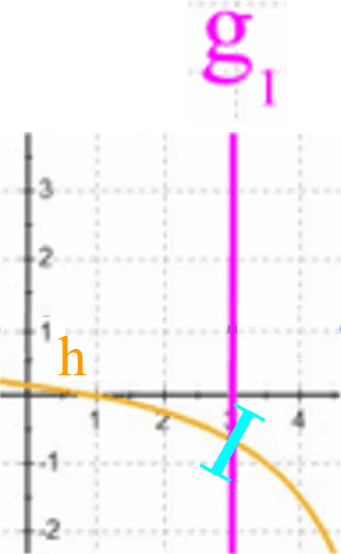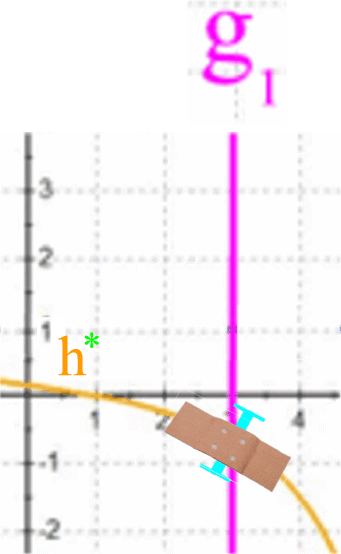
"Flicken" heißt dabei aber nicht, dass die
![]() efinitionslücke
x = 3 von h*
plötzlich verschwindet. Man könnte auch sagen: unter dem
Pflaster h**
bleibt die Wunde von h, sie wird
durch h**
zwar übertüntcht, aber nicht geheilt.
efinitionslücke
x = 3 von h*
plötzlich verschwindet. Man könnte auch sagen: unter dem
Pflaster h**
bleibt die Wunde von h, sie wird
durch h**
zwar übertüntcht, aber nicht geheilt.
Wenn eine gebrochen
rationale Funktion h* derart in einer
![]() efinitionslücke
"flickbar" ist, spricht man dort auch von einer "behebbaren Polstelle".
efinitionslücke
"flickbar" ist, spricht man dort auch von einer "behebbaren Polstelle".
Davon zu unterscheiden ist die
![]() efinitionslücke
x = 6, die
efinitionslücke
x = 6, die
auftritt, also nicht durch h** behebbar ist:
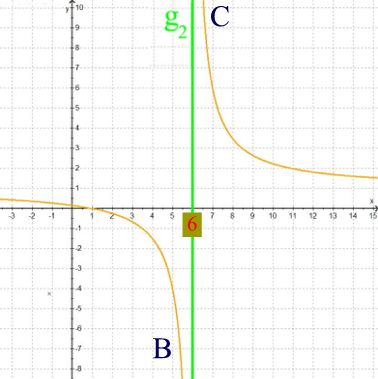
Wenn wir diese Lücke mit einem "Pflaster" flicken wollten, müssten wir den untersten Punkt des Zweigs B mit dem obersten Punkt des Zweigs C verbinden. Da beide Zweige aber unendlich weit nach unten bzw. oben laufen, gibt es solch einen untersten bzw. obersten Punkt überhaupt nicht. Bzw. wenn wir ein "Pflaster" benutzen wollten, müsste es unendlich lang sein:
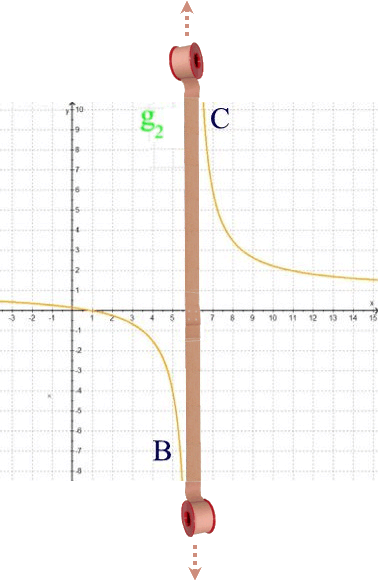
Man sagt auch: die Polstelle von h* bei x = 6 ist "nicht behebbar", da die Ersatzfunktion h** dort auch eine Polstelle hat.
Ein offenes Problem ist aber noch
"[...] dass die Quotientenfunktion h*
einerseits für x = 3 nicht definiert ist und
andererseits für x = 3 eine Nullstelle hat.
Beides gleichzeitig geht aber nicht."
Hier sei zum wiederholten Mal daran erinnert, dass man
zu allererst den
![]() efinitionsbereich
von h*
bestimmen
efinitionsbereich
von h*
bestimmen
(x = 3 aus ihm herausnehmen)
muss und erst danach
beispielsweise die Nullstelle(n) von h* bestimmen kann:
wenn aber
Nichtmal die "Flickstelle" ist eine Nullstelle, denn diese Flickstelle liegt ja bei y ≈ - 0,7, also unterhalb der x-Achse.
 |
Es sei nur kurz eingeschoben, dass die ursprüngliche
Quotientenfunktion
|
Alles Bisherige war eigentlich nur "Pflicht" oder Vorspiel, also Standard-Schulstoff.
Wirklich interessant (Kür) wird's erst, wenn wir uns anschauen, wie h langsam in h* übergeht, wenn wir also wie oben
f völlig unverändert lassen
bei g*
die Nullstelle N4 (6 | 0 ) unverändert lassen, aber
die Nullstelle N3 von N3 (4 | 0 ) nach N3 (3 | 0 ) wandern lassen:
Um Übersicht zu behalten, lassen wir im Folgenden
den Funktionsgraphen von f sowie
die Funktionsgraphen der aufeinander folgenden g
weg und zeichnen stattdessen nur
den Funktionsgraphen von h* sowie
die Funktionsgraphen der aufeinander folgenden h
(zur Unterscheidung jetzt in der neuen Farbe xxx )
ein:
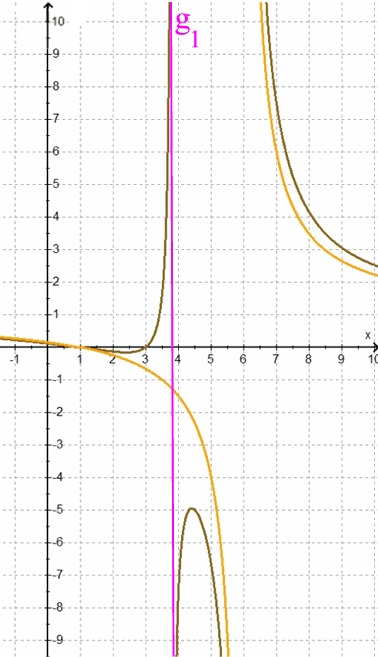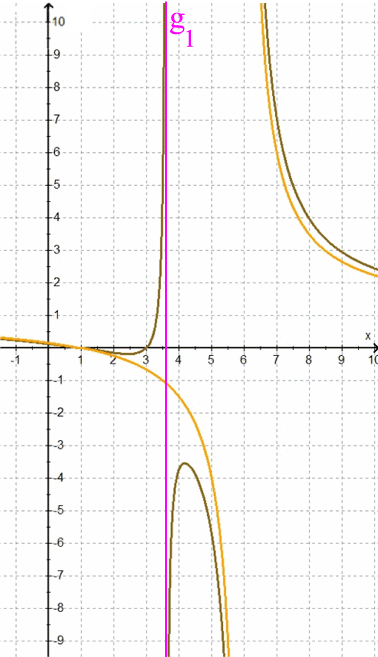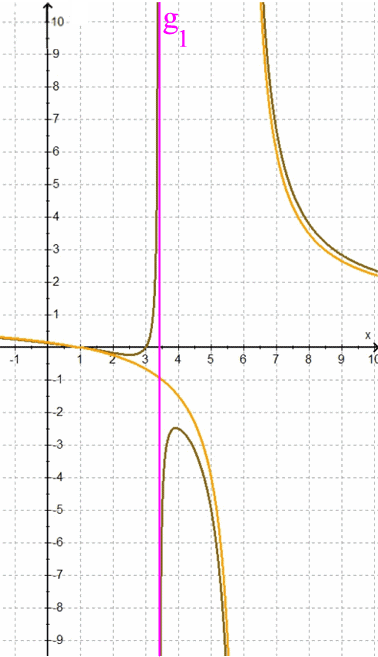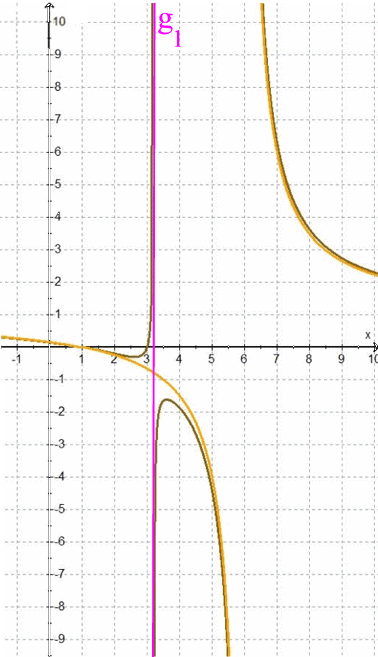
Die Funktionsgraphen der h wandern also immer näher an den Funktionsgraphen von h* heran, behalten aber im Gegensatz zu diesem immer noch die Asymptote g1 . Erst im allerletzen Augenblick
(wenn nämlich N3 (3 | 0 ) exakt gleich N2 (3 | 0 ) ist)
werden die asymptotischen Zweige
zusammengebogen
und geflickt
(wobei im Flicken noch immer ein punktförmiges Loch bei x = 3 bleibt):
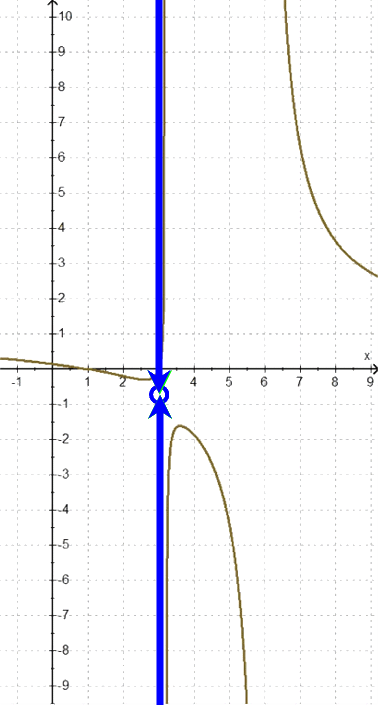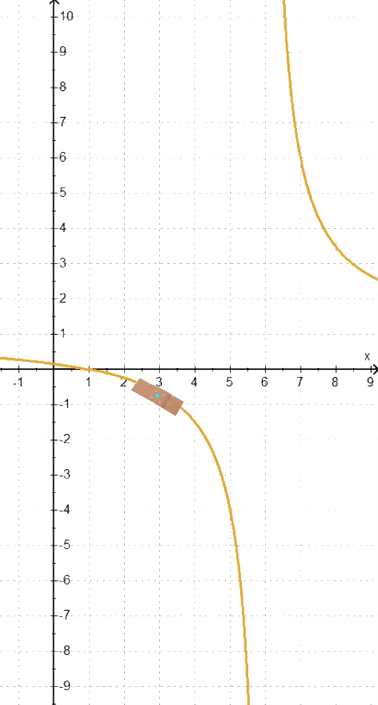
Man könnte auch sagen: der Fahrradschlauch hat bei x = 3
immerhin keinen langen Riss mehr,
sondern nur noch ein klitzekleines Loch.
Und dieses Loch lässt sich leicht mit
 h**:
y =
h**:
y =  beheben
beheben
(was allerdings letztlich auch nicht viel bringt, da an anderer Stelle, nämich bei x = 6, ein langer, nicht behebbarer Riss bleibt).
 |
|
Natürlich sollte man die Grundideen des Theorieteils verstanden haben. Danach aber lassen sich die dortigen Erkenntnisse spielend leicht auf Funktionen anwenden.
Ein einziges Beispiel:
gegeben sei die Funktion f mit der Funktionsgleichung f: y =
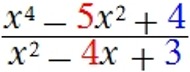 . Mit
dem Satz von Vietà
. Mit
dem Satz von Vietà
(4 + 1 = 5, 4 • 1 =
4,
3 + 1 = 4, 3 • 1 =
3)
und der zwischenzeitlichen Substitution x2 = z
((±2)2 = 4, (±1)2 = 1)
erhält man schnell
Man könnte die Funktionsgleichung also auch so schreiben:
f: y =
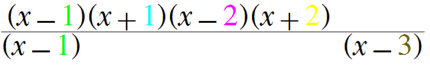
Zu allererst halten wir aber fest: die Nullstellen des
Nenners, also 1 und 3,
dürfen auf keinen Fall im Definitionsbereich auftauchen. Wir erhalten also
![]() \ {
1 ; 3 } und wissen somit, dass für
1 und 3 Polstellen
vorliegen:
\ {
1 ; 3 } und wissen somit, dass für
1 und 3 Polstellen
vorliegen:
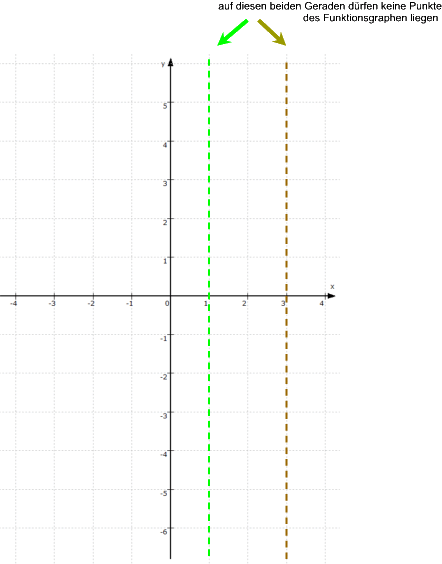
Bislang wissen wir aber noch nicht, ob bei
1 und 3 behebbare oder
nicht behebbare Polstellen vorliegen. Wie aber an
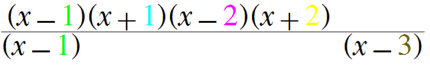 zu
erkennen ist, kommt
zu
erkennen ist, kommt
die Nullstelle 1 sowohl im Zähler als auch im Nenner vor (und zwar gleich oft), d.h. wir können sie "rauskürzen" und es liegt dort eine behebbare Polstelle vor,
die Nullstelle 3 nur im Nenner vor. , d.h. wir können sie nicht "rauskürzen" und es liegt dort eine nicht behebbare Polstelle vor:
f: y =
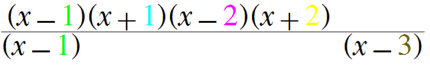 =
=
=
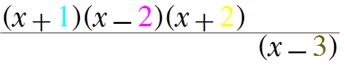
Nun heißt aber
"behebbar", dass bei 1 nur eine klitzekleine Definitionslücke vorliegt,
"nicht behebbar", das bei 3 eine Asymptote vorliegt:
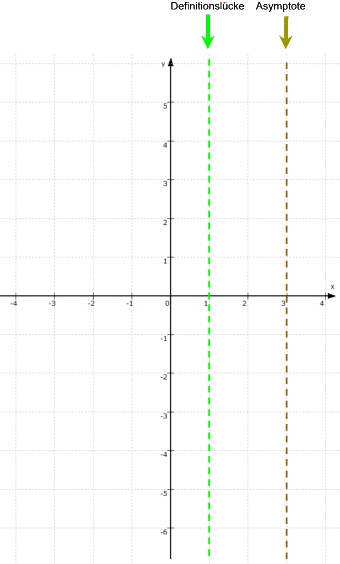
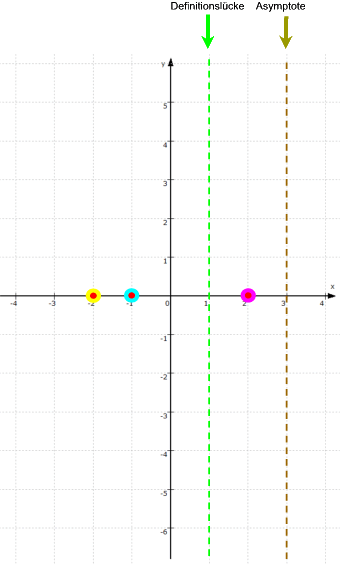
Des weiteren wissen wir, dass die Nullstellen der Funktion f identisch mit denjenigen des Zählers sind
(jetzt allerdings ohne 1),
d.h. f hat die Nullstellen -1, 2 sowie -2 :
Des Weiteren gilt für sehr große x ganz links und ganz rechts:
f: y =
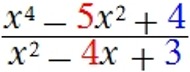 =
=
 ≈
≈
![]() = x2
,
= x2
,
d.h. der Funktionsgraph von f sieht ganz links und ganz rechts annähernd aus wie die Normalparabel:
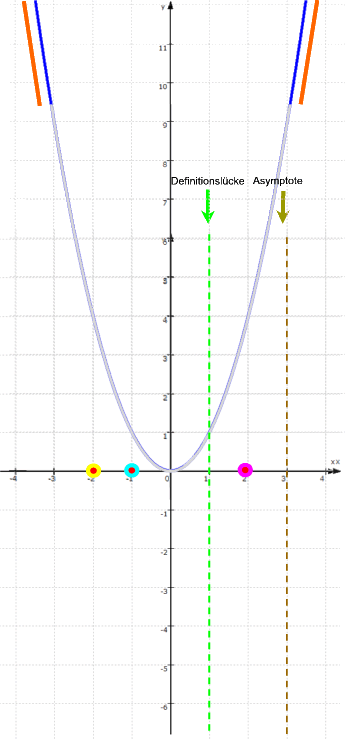
Wenn man nun all diese Informationen zusammensetzt, bleibt überhaupt nur noch ungefähr folgender Funktionsgraph von f:
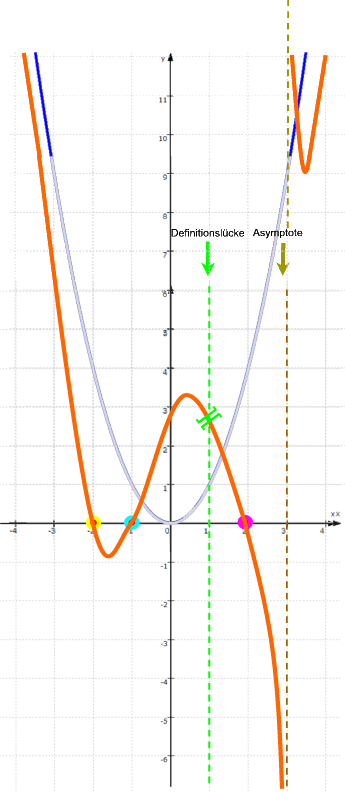
Hier stimmt noch etwas nicht beim "Ast" ganz rechts oben, und überhaupt sind alle Maße nur sehr ungefähr. Aber dennoch ist der grundsätzliche Verlauf des Funktionsgraphen klar, der korrekt so aussieht:
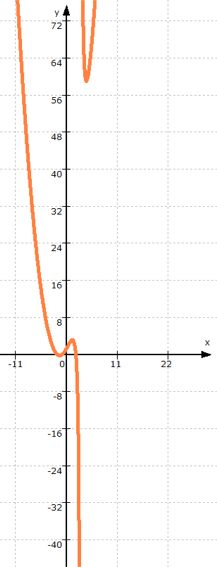
Und es ist doch insbesondere bei den nicht ganz einfachen Rechnungen zu gebrochen rationalen Funktionen schön, wenn man schon vorher eine Vorstellung vom Funktionsgraphen hat und somit beispielsweise auch weiß, was die Rechnung hinterher hoffentlich bestätigt, nämlich dass er z.B. zwei lokale Minima und ein lokales Maximum hat.
Ein Computer-Funktionenplotter, der einem sofort

anzeigt, ist da keine Alternative, weil dann keinerlei eigener Gehirnschmalz mehr zu investieren ist, sondern das fix und fertige zeichnerische Ergebnis nur noch durch schnöde Rechnung bestätigt werden kann, während bei unseren Vorüberlegungen ja erst die (somit überhaupt erst notwendige) Rechnung zeigen kann, wo genau beispielsweise die Minima und das Maximum liegen.
Das leicht morbide Kokettieren mit einem Knochenbruch

rächt sich natürlich schnell: wenige Monate später ist aufgrund eines Rodelunfalls die Funktion meines rechten Fußes auch gebrochen-rational:
"Selbst der gute Onkel Fritze
sprach: »Das kommt von dumme Witze«."
(Wilhelm Busch)
Jahre später erfahre ich aus dem Buch
 :
:
"Dabei bedeutet al-gabr oder al-dschabr [modern »Algebra«] [...] eigentlich das »Einrenken« eines ausgerenkten Knochens [...]"
Und wo ich schon das Buch
 zitiere, entnehme ich ihm auch noch eine andere Weisheit: unsere
"arabischen" Zahlen inkl. des Dezimalsystems und der so wichtigen Null haben die
Araber "indisch" genannt. Und was angeblich erstmals in Indien
entdeckt wurde, hatten in Wirklichkeit schon viel früher die Sumerer
und Babylonier: gute Ideen sind oft viel älter, als man denkt.
zitiere, entnehme ich ihm auch noch eine andere Weisheit: unsere
"arabischen" Zahlen inkl. des Dezimalsystems und der so wichtigen Null haben die
Araber "indisch" genannt. Und was angeblich erstmals in Indien
entdeckt wurde, hatten in Wirklichkeit schon viel früher die Sumerer
und Babylonier: gute Ideen sind oft viel älter, als man denkt.
(z.B. war Descartes keineswegs der erste, der das nur nach ihm benannte "kartesische Koordinatensystem" benutzt hat; was keineswegs heißen muss, dass er es geklaut hat, sondern ebenso gut bedeuten kann, dass er es neu erfunden hat).