ein (einziges!) Gegenbeispiel
oder mathematisches vs. alltägliches Denken

"Alle Schwäne sind weiß - bis wir nach Münster kommen, wo die schwarze Schwänin Petra in heißer Liebe ihr (weißes) Schwanentretboot umpaddelt. Für eine Wissenschaft, die auf Induktion setzt, ist das Gegenbeispiel wie ein Ganove, der nur darauf wartet, die unschuldigen Hypothesen mit seiner Keule platt zu machen, wenn sie an ihm vorbeikommen. Man sucht daher ganz gezielt eine Begegnung mit diesem finsteren Gesellen und begibt sich dazu in Regionen, wo die Gefahr am größten ist, dass er lauert. Die besten Experimente sind so angelegt, dass sie eine bestimmte Aussage, die aus der Hypothese folgt, auf einen Bereich zuspitzen, wo sie am ehesten widerlegt werden können. Die Falsifizierbarkeit unterscheidet eine wissenschaftliche Hypothese vom bloßen Glauben - und die Wissenschaften von anderen Hochburgen der Meinungen und Behauptungen."
(zitiert nach , S. 17 )

An diesem bildschönen Zitat ist doch allerlei bemerkenswert:

  1. , was doch arg meinen Lokalpatriotismus bauchpinselt: dass in einem amerikanischen Buch meine Heimatstadt Münster als experimentum crucis wissenschaftlichen Denkens dient :-)

(dieser affige Schwan auf dem Aasee und seine Weltberühmtheit, aus der die Münsteraner derzeit ca. 73 % ihres Selbstbewusstseins saugen).

  1. die "Verkehrung" des wissenschaftlichen (mathematischen) gegenüber dem alltäglichen Denken, hier ausgedrückt durch das Bild des Ganoven: im alltäglichen Leben würde jeder

(also - und das wird noch wichtig - auch jeder Mathematiker)

die Begegnung mit solch einem Ganoven vermeiden wollen, während Wissenschaftler sie (angeblich) auf geradezu masochistische (oder heldenhafte?) Art regelrecht suchen.

  1. ein an Karl Popper angelehnter Wissenschaftsbegriff, also die Vorstellung, dass die "Falsifizierung" in den Wissenschaften nicht bloß ein leider unvermeidbarer Betriebsunfall ist, sondern bewusst angesteuert werde. Mehr noch: dass diese Falsifizierung geradezu der Motor aller Wissenschaften sei.

(Ob das eigentlich so eindeutig stimmt, darauf wird zurückzukommen sein.)

  1. und für meine weitere Argumentation eher unwichtig: wenn man die Worte der Autoren auf die Goldwaage legen will, eine allzu pauschale (negative) Vorstellung von "Glaube", der prompt mit "Meinungen und Behauptungen" gleichgesetzt wird.

Allemal Recht haben die beiden Autoren aber mit ihrem Hinweis, dass in den Naturwissenschaften und insbesondere in der Mathematik (dem eigentlichen Thema ihres Buchs) oftmals gezielt nach einem Gegenbeispiel gesucht wird bzw. dieses einen ganz besonderen mathematischen Rang, ja manchmal sogar eine enorme (Ganoven-)Dramatik hat.

Um das genauer zu untersuchen, nehmen wir uns ein besonders hübsches (eindrückliches), bewusst rein innermathematisches Beispiel:

nach einigem Rumspielen mit Zahlen mag man vielleicht auf folgenden Effekt stoßen:

(Nebenbei: weil es zu schön ist, zum wahr zu sein, glaube [schlucke] man es nicht einfach, sondern überprüfe es mal [immerhin mit dem Taschenrechner]: das kommt tatsächlich so raus!)

Da entstehen also nacheinander durch die Multiplikation simpler natürlicher Zahlen

(deren Ziffern nur simple Einsen sind)

immer wieder sogenannte "Palindrome", also Zeichenfolgen, die symmetrisch, also von vorne und hinten gelesen gleich sind (vgl. etwa OTTO oder ANNA).

Mehr noch, auch diese Palindrome sind wieder ganz einfach, nämlich immer hübsch in Einerschritten erst "treppauf" und dann "treppab"

(so dass nebenbei immer jede vorherige "Treppe" in der nächstfolgenden auftaucht und nur eine weitere [höhere] Stufe dazwischengequetscht wird):

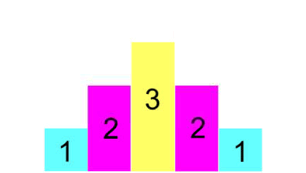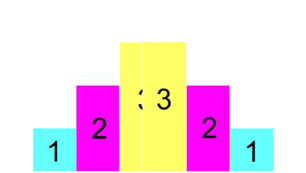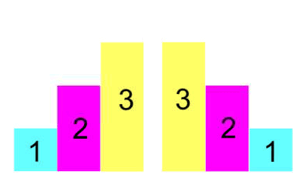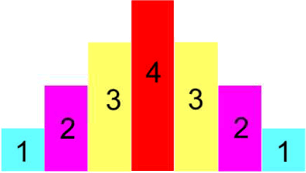
Halten wir hier schonmal inne, weil so vieles keineswegs selbstverständlich ist:

  1. nämlich schon

"nach einigem Rumspielen mit Zahlen mag man vielleicht auf folgenden Effekt stoßen":

ich bin nie auf diesen Effekt gestoßen, sondern habe ihn mir irgendwo "angelesen". Wieso sollte ich auch den Versuch machen, Zahlen aus Einser-Ziffern miteinander zu multiplizieren??? - zumal ich ja nicht vorher wüsste, dass sich das lohnen könnte.

Natürlich habe ich des öfteren 1 ● 1 = 1 und 11 ● 11 =  121 gerechnet, ja, das muss ich nichtmal mehr rechnen, sondern weiß es auswendig. Aber an diesen beiden ersten Ergebnissen 1 und 121 fällt einem (?) wohl noch kaum etwas auf, bzw. wenn der bewusste Effekt einem auffällt, erscheint er wohl nur als rein zufällig und daher nicht weiter bemerkenswert

(an nur zwei Beispielen lässt sich kaum eine Regel erkennen und vermuten).

Zu 111 ● 111 (und damit dem Ergebnis 12 321) bin ich allerdings nie vorgestoßen, was wohl auch daran liegt, dass diese Berechnung schon ganz erheblichen Aufwand erfordert.

(Dieser rasant zunehmende Rechenaufwand wird unten noch wichtig.)

Mehr noch: der genannte Effekt fällt einem wohl auch nur dann auf, wenn man 1 ● 1 = 1, 11 ● 11 =  121 und 111 ● 111 = 12 321 nicht zu verschiedenen Zeiten, sondern - aus welchem Anlass eigentlich? - direkt nacheinander rechnet und zudem (gar nicht so selbstverständlich) einen Sinn für (symmetrische) Ziffernfolgen hat

(was einem zumindest im Deutschen dadurch erschwert wird, dass wir Zahlen ja oftmals in "falscher" Reihenfolge und "entstellend" lesen, nämlich z.B. 121 als "(ein)hunderteinundzwanzig" statt "einhundertzweizehneins").

Und wann denn sonst spielt in der Mathematik die Ziffernfolge jemals eine Rolle?!

Aber offensichtlich ist doch irgendjemand mal auf den besagten Effekt gestoßen, und da wird man trotz puren Nachvollzugs doch doppelt staunen dürfen

(hoffentlich noch staunen können!):

  1. , dass dieser jemand (wie auch immer) überhaupt drauf gekommen ist (aufmerksam genug war),

  2. , dass der Effekt so wunderschön simpel-elegant funktioniert.

  1. kann man an dem doch recht simplen Beispiel wunderbar erkennen, wer ein "richtiger" Mathematiker ist. Bzw. ob jemand ein "richtiger" Mathematiker ist oder, wenn er an solch einem Beispiel erst mal "Blut geleckt" hat, werden kann, entscheidet sich nicht an höchstkomplizierten Rechnungen, sondern an ganz simplen "Einstellungen".

(Ich habe dabei "an solch einem Beispiel" statt "an diesem Beispiel" geschrieben: ich fände es doch arg einseitig, die mathematische "Eignung" von einem einzigen Beispiel abhängig zu machen. Vielmehr hoffe ich, dass in der Schulzeit viele Beispiele vorkommen und für alle SchülerInnen ein Beispiel dabei ist, an dem sie Feuer fangen könnten.
Kommt hinzu, dass die Beispiele nicht alle - wie das vorliegende - "zahlentheoretisch" sein dürfen: es gibt auch andere Zugänge zur "richtigen" Mathematik.
Und die genannten "Einstellungen" bringt man vielleicht nicht a priori mit, sondern muss man ab und zu begeistert vorgemacht bekommen, so dass sie hochinfektiös werden.)

Woran nun also entscheidet sich im vorliegenden Fall, ob jemand ein "richtiger" Mathematiker ist?:

  1. daran, ob er das bewusst rein innermathematisch gewählte Beispiel überhaupt staunenswert findet - oder aber sagt: "ist mir doch herzhaft egal, ob da symmetrische Ergebnisse rauskommen - und was »hat« man eigentlich davon?"

  2. daran, ob er sich sofort fragt (ihn diese Fragen reizen):

  1. "geht das eigentlich immer, gilt also auch 1111 ● 1111 = 12 34 321 usw.?"

  2. vielleicht auch: geht das vielleicht auch ähnlich für 2 ● 2 , 22 ● 22 , 222 ● 222...?

(Dieser Fall B. - und somit das erste Gegenbeispiel - sei sehr kurz abgehakt:

       2 ●     2 =     4  

     22 ●   22 =   484     : da scheint wieder eine Regel zustande zu kommen,

   222 ● 222 =49284  : hier ists mit der [klaren] Regel aber schon vorbei.)

Bleiben wir also bei der Frage A., d.h.

"geht das eigentlich immer, gilt also auch 1111 ● 1111 = 12 34 321 usw.?"

Hier zäumen wir das Pferd mal von hinten auf: es müssten nacheinander folgende Ergebnisse zustande kommen:

Wie aber ginge die Regel dann weiter?:

Eine Möglichkeit wäre:

Wir würden lso die Ziffern (!) der Zahl (!) 10 einfügen, und in dieser Logik wäre das nächste Ergebnis dann

123456789101110987654321

Wichtig daran ist: dabei kommen allemal denkbare Zahlergebnisse zustande.

Aber kommen denn immerhin nacheinander

heraus?

Oben war allzu unauffällig nebenher gesagt worden:

"an nur zwei Beispielen lässt sich kaum eine Regel erkennen und vermuten"

Ab wie vielen Beispielen

"Aller guten Dinge sind drei", d.h. mir scheint ja doch, dass

schon sehr überzeugend sind.

Nun entspricht die mathematische Einstellung, irgendwo ein Gegenbeispiel (den Ganoven) zu vermuten, aber eben keineswegs der alltäglichen Einstellung.

Und es scheint mir durchaus bedeutsam, dass auch Mathematiker zeitweise "Alltagsmenschen" sind: auch sie werden ja erstmal eine allgemeingültige Regel vermuten - und dann erst setzt ihre angelernte Skepsis ein.

Genauer: sie werden möglicherweise zwei Strategien fahren:

  1. noch einige weitere Beispiel ausprobieren

(wobei sich eventuell schon ein Gegenbeispiel ergibt; vgl. b.B.),

  1. dann, wenn alle bisherigen Beispiele die Regel erfüllten,

  1. einen allgemeingültigen Beweis probieren,

  2. ein Gegenbeispiel (den Ganoven) suchen.

Auch hier zäume ich das Pferd wieder von hinten auf, fange also mit b. statt mit a. an:

man muss sich nämlich mal in aller Drastik und Dramatik klar machen, was b.A. und b.B. tatsächlich bedeuten würden:

Das hört sich zwar nett an, aber es ist doch gleichzeitig auch für alle anderen, die einen allgemeingültigen Beweis versucht haben, ungemein frustrierend: da haben sie vielleicht Jahre mit dem Beweisversuch verbracht, und dann kommt ein Besserwisser und Klugscheißer (ein einziges Gegenbeispiel), das all diese Versuche als unsinnig und überflüssig erweist.

Überhaupt beweist ein (einziges) Gegenbeispiel "nur", dass die vermutete Regel in einem einzigen Fall nicht gilt. Es wäre also durchaus denkbar, dass es kein einziges weiteres Gegenbeispiel gibt, die Regel also durchaus (weiterhin) in allen anderen Fällen gilt.

Das Gegenbeispiel zeigt also eventuell nur, dass die wunderbare Regel "mit einer einzigen Ausnahme immer" (weiterhin) gilt.

Nun ist es aber Einstellungssache, wie man auf diese Botschaft reagiert:

  • für den "richtigen" Mathematiker ist die Regel mit diesem einzigen Gegenbeispiel endgültig ruiniert

   ,

und unser "richtiger" Mathematiker kümmert sich damit auch nicht mehr um evtl. vorhandene andere Gegenbeispiel; er hat also mit dem einen Gegenbeispiel sozusagen endgültig die Lust verloren;

  • der "Alltagsmensch" wird aber doch sagen: "die Ausnahme bestätigt die Regel", d.h. die Regel hat keineswegs ihre Überzeugungskraft verloren.

Anders gesagt:

  • mathematisch besagt ein einziges Gegenbeispiel ALLES,
  • im Alltagsleben besagt es GAR NICHTS oder kann höchstens einen ersten Zweifel schüren.

Worauf ich mit all dem hinaus will

(und wofür unsere vermutete Regel nur ein fast schon beliebiger, wenn auch - wie ich finde - besonders schöner Anlass ist):

  1. das "alltägliche" und das mathematische Denken sind Lichtjahre voneinander entfernt;

  2. das mathematische Denken ist nicht "richtiger" als das "alltägliche", und deshalb ist das (über die Mathematik hinausgehende) Erziehungsziel, SchülerInnen sollten skeptisch gegenüber sämtlichen (auch außermathematischen) allgemeinen Behauptungen sein, zwar höchst ehrenwert, aber doch äußerst schwer zu erreichen;

  3. und wie oben schon angedeutet: auch MathematikerInnen sind (was sie auf altkluge Art oftmals leugnen) zeitweise oder sogar zeitgleich "Alltagsmenschen".

(Dass mathematisch-naturwissenschaftliches Denken vor Torheit nicht schützt, zeigt beispielsweise folgender Fall:

Und ich - zusammen mit einiger neuerer Wissenschaftstheorie - mag auch nicht recht glauben, dass Forschung so glasklar "poppersch" abläuft, wie die Autoren es in dem Zitat oben noch annahmen:

  • jeder will doch wohl seine Thesen eher bestätigt als widerlegt wissen

(in einem Altenheim hieß es letztens: "wir freuen uns über ihre [Negativ-]Kritik": Blödsinn!),

  • der poppersche Ansatz übersieht völlig die Rolle von Intuition und Ästhetik in der Forschung, ist also einseitig rationalistisch.)

Um 1. und 2. genauer zu erläutern:

selbstverständlich kann man im Alltagsleben schöne Parallelbeispiele für "Gegenbeispiele" finden.

Eins meiner Lieblingsbeispiele dabei ist, dass ich früher immer der Meinung war, sämtliche Türken, soweit sie nicht gerade Babys oder Greise mit Glatzen bzw. längst grauhaarig sind, seien schwarzhaarig

... bis ich dann den ersten "semmelblonden" Türken kennenlernte.

Was bedeutet nun dieses (bis heute) einzige Gegenbeispiel?:

  • "mathematisch" gesehen: die Behauptung, sämtliche Türken seien schwarzhaarig, ist gnadenlos falsch, gehört also endgültig auf den Müllberg der (per definitionem grundsätzlich falschen) Vorurteile;

  • dennoch wird es aber wohl weiterhin zutreffen, dass die allermeisten Türken schwarzhaarig sind.

Das "schwarzhaarige Türken"-Vorurteil hat allemal den Vorteil, dass es nicht rassistisch ist. Wirklich gefährlich sind aber natürlich die tatsächlich rassistischen Vorurteile, die - und das ist wichtig! - durchaus mit einigem Grund immun gegen (wenige) Gegenbeispiele sind, also beispielsweise in der Nazi-Zeit

(wobei mir der Nazi-Knüppel fast schon peinlich, das Beispiel aber eben doch sehr erhellend ist):

"Der Kurzwarenhändler Ismael Rosenstein bei mir um die Ecke ist ja wirklich nett, aber all die anderen Juden ...?!"

(Vgl.

"»Mein« Achmed in der Dönerbude bei mir um die Ecke ist ja total nett [ich duze ihn sogar], aber all die anderen Türken ...?!"

Noch interessanter ist fast der "Ausländerhass ohne Ausländer", den es lange Zeit in der ehemaligen DDR gab bzw. sogar wohl noch gibt: man kannte nur die Vorurteile gegenüber Ausländern ohne jedes konkrete [Gegen-]Beispiel.)

Die Wirkungslosigkeit des Gegenbeispiels lässt sich aber keineswegs so einfach "mathematisch" aufheben, weil da von zwei (mathematisch gar nicht erfassbaren) völlig unterschiedlichen "Judentypen" die Rede ist:

  • einerseits einem (einzigen!) konkreten Juden "vor Ort",

  • andererseits aber massenhaft "virtuellen" (angeblich schlechten) Juden

(Nebenbei eine Frage, die man nach wie vor kaum stellen darf: was beweist eigentlich ein konkreter schlechter [?] Jude?: vgl. seinerzeit die Kontroverse um Rainer Werner Fassbinders Theaterstück "Der Müll, die Stadt und der Tod".)

Mir scheint vielmehr, dass Vorurteile im Alltagsleben anders unterwandert werden müssen:

  • durch viele Gegenbeispiele, so dass man langsam immer mehr von bisherigen Denkgewohnheiten wegkommt,

  • falls es einem an sozialer Phantasie fehlt: durch konkrete Beispiele

(z.B., was es konkret heißt, von Hartz IV leben zu müssen; irgendwann spart man sich dann vielleicht Sprüche wie "die Arbeitslosen wollen doch ALLE gar nicht arbeiten").

Damit aber zu b.a., also

"noch einige weitere Beispiel ausprobieren".

Das aber sagt sich so leicht, weil man da schon ganz erhebliche Rechnungen ausführen muss, nämlich

Das ist "mit der Hand" äußerst mühsam, und leider hilft einem da auch kein Taschenrechner, denn beispielsweise beim letzten ausgeschriebenen Beispiel 111111111 ●   111111111 zeigt der als Ergebnis an:  1.23456789876543 ● 1016, d.h. dem Taschenrechner wurde das Ergebnis zu groß, und deshalb zeigt er nur  1.23456789876543 ● 1016 , was ausgeschrieben 12345678987654300 bedeutet.

Nun stimmt da unsere vermutete Regel zwar weitgehend, aber eben nicht mehr am Ende, also bei 00, wo wir doch 21 erwartet hätten.

Der Rechner da natürlich wegen der allzu großen Zahl gerundet haben, aber wir wissen halt nicht, ob  er gerundet hat. Und wenn er gerundet hat, wissen wir nicht, wie er gerundet hat. Beispielsweise hätte er auch die beiden korrekten Endstellen 49 zu 00 gerundet haben können.

Solche praktischen Überlegungen scheinen mir aber nun keineswegs nebensächlich zu sein: wenn das Rechnen allzu umständlich, ja regelrecht aussichtslos wird, wird der Laie vermutlich aufgeben und

Nun gibt es aber auch "bessere" Computerrechner, die mit mehr stellen arbeiten, und dan ergibt sich dann:

Die vermutete Regel gilt also in der Tat bis hin zu Zahlen aus neun Einserziffern!

Und doch scheitert sie genau an der Stelle, die wir oben schon vermutet hatten: bei der Zahl aus zehn Einserziffern ergibt sich

          1111111111 ●      1111111111 = 1234567900987654321

Oder genauer: das folgt noch weitgehend der vermuteten Regel, aber es fehlt doch die 8 in 12345678900987654321

(und außerdem wird bei 00 etwas anderes eingeschoben, als wir es oben vermutet hatten).

Und schon scheiden sich wohl wieder die Geister:

PS:

Eine durchaus interessante Frage, der hier allerdings nicht weiter nachgegangen werden soll, ist, warum das eigentlich bis zu neun Einsen zu schön klappt - und bei zehn Einsen nicht mehr.