wie funktioniert das?:

auch das ist Geometrie:
wie
funktioniert das?:

Eines der wichtigsten Bücher sowohl der Physik- als auch der
Mathematik-Geschichte, nämlich Isaac Newtons
 , trägt einen
bemerkenswerten Titel, nämlich auf Deutsch „Die mathematischen Prinzipien der
Naturphilosophie“
, trägt einen
bemerkenswerten Titel, nämlich auf Deutsch „Die mathematischen Prinzipien der
Naturphilosophie“
(was ja - nebenbei gesagt - ein enorm selbstbewusster, wenn nicht gar arroganter Titel ist).
Aus heutiger Sicht stellt sich aber die Frage, was da die Philosophie zu suchen hat, wenn in dem Buch doch von Natur (Physik) und Mathematik die Rede ist.
Für das Vorkommen der Philosophie im Titel dieses Buches gab es damals (1687) zwei Gründe:
(Newton hat erheblich dazu beigetragen, es überhaupt erst zu etablieren),
sondern alle Weltbetrachtung war Teil der Philosophie oder Theologie,
(was leider ein wenig abhanden gekommen ist: schon seit Galilei haben sich Theologie und Naturwissenschaften, aber eben auch Philosophie und Naturwissenschaften einander entfremdet).
Newtons geniale Leistung bestand darin, die Natur mathematisch erfassbar zu machen. Er war also zentral daran „mitschuldig“, dass die Mathematik geradezu zur Sprache und zum Wahrheitsindikator der Naturwissenschaften
(und heutzutage oftmals such der Sozial- und Wirtschaftswissenschaften)
geworden (verkommen?) ist.
In dem Buch geht es - physikalisch gesehen - um die Bewegung von Körpern
(was damals eine Sensation war: sowohl auf
der Erde als auch im Universum:
 ),
),
und zwar um
(z.B. der Bahn des Mondes um die Erde),
für deren mathematische Beschreibung Newton (und Leibniz) überhaupt erst ganz neue Lösungsverfahren entwickeln musste, nämlich die Differential- und Integralrechnung
(die noch heute zentrales Thema der Oberstufenmathematik an Schulen ist).
Nun ist die Differential- und Integralrechnung im Laufe der Zeit eben auch ein (enorm wichtiges) rein innermathematisches Gebiet geworden, und die Schulmathematik versteht sich ja oftmals auch
(mit gutem Grund!)
als „reine“, also ausschließlich innermathematische, d.h. weitgehend an (physikalischen) Anwendungen desinteressierte Mathematik.
So ist dann in der Schulmathematik auch Newtons physikalischer Anlass (beschleunigte Bewegungen) weitgehend vergessen worden, bzw. wenn‘s hoch kommt, wird da zur Illustration der Differentialrechnung mal kurz der freie Fall erwähnt

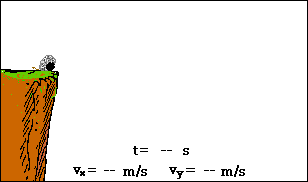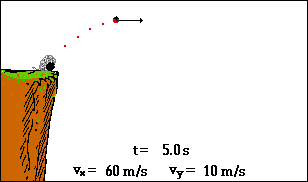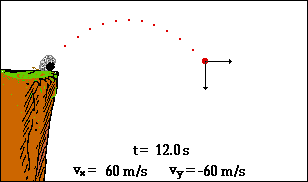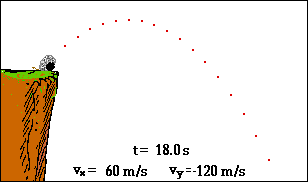
- und dann wieder schnell in die reine Mathematik abgehoben.
Dennoch wundert es mich, dass die Schulmathematik weitgehend statisch ist. Nur zwei Beispiele:
(z.B.
 ),
),
also so, als wenn nichts zwischendurch passiert wäre, wodurch die an sich doch simplen Kongruenzabbildungen
(jeder Schüler hat schon häufig Gegenstände verschoben, gedreht und gespiegelt [z.B. ein Buch umgedreht] und weiß intuitiv ziemlich genau, was sich dabei ändert - und was nicht)
doch unnötig unanschaulich, also verkompliziert werden.


(Einzige Ausnahmen sind da Wendepunkte, bei denen Links- in Rechtskurven [oder umgekehrt] über“gehen“.
Nebenbei: sogenannte „Dynamische Geometrie“-Software wie
z.B. ![]()
[und als Vorläufer meine uralte Programmsammlung
![]() Bewegte
Bewegte
 Mathematik ]
Mathematik ]
macht endlich vermehrt Bewegungen sichtbar.
Und doch ziehe ich, wenn irgend möglich, die Bewegung
realer Gegenstände einer letztlich nur virtuellen Bewegung auf dem
Computerbildschirm vor. Vgl.
![]()
 )
)
Mittels Bewegung können die Schüler ihr räumliches Vorstellungsvermögen verbessern, das eine wichtige Voraussetzung für mathematisches Denken ist - und sogar für zunehmend abstrakte Sachverhalte.
Vgl. etwa
"Räumliches Vorstellungsvermögen ist grundlegend für den
Aufbau des Zahlenraums. Zahlen bilden „...einen, allerdings für jeden Menschen
individuellen Raum, wobei diese Vorstellung oder Visualisierung nicht Abbild
irgendeines konkreten Objektes ist, sondern vom einzelnen konstruiert wird.“
(Lorenz, J.H., 1987a, S. 171; vgl dazu auch Lorenz, J.H., 1992, S.137ff). Der
Schüler konstruiert sich einen Vorstellungsraum, in dem die Zahlen eine
räumliche Anordnung haben. Wir hoffen oder gehen davon aus, dass dieser Raum
eine dem Arbeitsmittel ähnliche Anordnung besitzt.
Der Schüler bewegt sich
nun „mathematisch“ in diesem imaginären Raum [...]"
(Quelle:
![]() )
)
Ein Beispiel zur Übung räumlicher Vorstellung:
(z.B. mittels Bohrmaschine)
um seine Mittelachse rotieren
 und erhalten einen Zylinder
und erhalten einen Zylinder
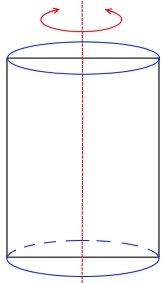 ;
;
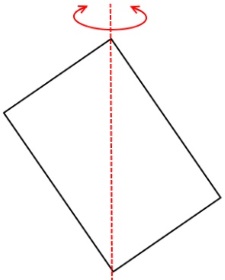 und
erhalten den
aus
Kegelteilen zusammengesetzten Körper
und
erhalten den
aus
Kegelteilen zusammengesetzten Körper
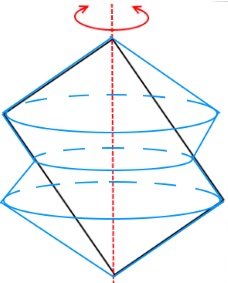 .
.Die dabei entstehenden "Körper" sind natürlich nur optische Täuschungen
(virtuell), weil unsere Augen zu langsam für hohe Drehgeschwindigkeiten sind und
deshalb eine Folge von Einzelbildern fälschlich als Gesamt"körper" wahrnehmen.
Trotzdem fallen unsere Augen aber nicht ganz auf diese Täuschung rein, da sie
nach wie vor durch den entstehenden Körper hindurch sehen können. Die entstehenden
"Körper" haben also etwas Gespensterhaftes
 und sind somit eine
Vorstufe der Abstraktion.
und sind somit eine
Vorstufe der Abstraktion.
Und irgendwann kann man dann dazu übergehen, solche Drehungen "nur" noch im Kopf auszuführen:
Bemerkenswert an den echten wie auch an den “Gedanken(dreh)experimenten“ ist, dass sich da
(anders als im üblichen Unterricht bei Kongruenz- und Ähnlichkeitsabbildungen)
ein Gegenstand (ein zweidimensionales Rechteck)
in einen völlig
anderen (u.a. dreidimensionalen) Gegenstand verwandelt, der im zweiten Fall,
also bei
 , nichtmal einen Namen hat
, nichtmal einen Namen hat
(... eine Verwandlung, wie wir
sie ähnlich gleich auch bei
 wiedersehen
werden).
wiedersehen
werden).
Oder genauer: da wird mittels des einen (zweidimensionalen) Gegenstands ein anderer (dreidimensionaler) Gegenstand erzeugt.
"[...] Howards Behauptung, daß sich
Wolken vereinen, ineinander übergehen
und sich auflösen in eindeutigen und
erkennbaren Stufen."
(zitiert nach
 )
)
Damit nun aber endlich zu
auch das ist Geometrie:
wie
funktioniert das?:

(Das ist nun zwar keine 3D-, dafür aber endlich mal bewegte Geometrie [s.o.])
Mit "wie funktioniert das?" wird danach gefragt, ob die kontinuierlichen Übergänge einer oder mehreren Regeln gehorchen - und wenn ja: welcher bzw. welchen?
Wenn nun aber ein Mathelehrer schon so blöd fragt, ist das vermutlich eine rhetorische Frage in dem Sinne, dass die implizit mitgelieferte Antwort "ja" ist, also "die Übergänge gehorchen in der Tat einer oder mehreren Regeln", und zwar einer Regel oder mehreren Regeln, die dem Mathelehrer "natürlich" längst bekannt ist / sind, den Schülern aber (noch) nicht.
Man könnte sogar die Absicht unterstellen, dass die Schüler die Regel(n) nicht finden und im Gegensatz zum ach so schlauen Mathelehrer dumm sind.
Als ich mich an
 begeben
habe, dachte ich, dass ich die Regel(n) "natürlich" schnell finden würde
begeben
habe, dachte ich, dass ich die Regel(n) "natürlich" schnell finden würde
(und die Regel[n] auch für Schüler relativ einfach zu finden wäre[n]).
Ich werde unten aber noch zeigen, dass mir das auch nach längerer Arbeit an dem Problem nicht
(oder genau genommen: nur teilweise)
gelungen ist, worüber ich erst doch arg enttäuscht war, weswegen ich gedacht habe, dass
Erst im Nachhinein ist es mir gelungen, aus der Not eine Tugend zu machen, also meinem "Versagen" doch etwas Positives abzugewinnen
(oder es in eine didaktische Meisterleistung umzudeuten)..
Aber dazu ganz am Ende mehr.
Nochmal zu der gesuchten Regel bzw. den Regeln: Hauptgrund dafür, dass ich sie finden wollte, war schlichtweg, dass ich die Verwandlung

"einfach schön" finde
(und vielleicht geht es Schülern ja genauso).
Nun ist Schönheit aber schwer zu definieren. Ich versuch's erstmal so: ich finde die "gleitende Verwandlung" der Flächen schön.
Und da möchte ich doch wissen, wie sie zustande kommt, d.h. nach welcher Regel bzw. welchen Regeln sie vor sich geht.
Oder anders gefragt: wie hat der Designer / Programmierer
 konstruiert?
konstruiert?
Eine (erste) Regel wird man in
 vielleicht
doch schnell entdecken, nämlich dass die Bewegung periodisch ist: nach einer
Umdrehung des hellgrüne "Zeigers" fängt alles wieder von vorne an
vielleicht
doch schnell entdecken, nämlich dass die Bewegung periodisch ist: nach einer
Umdrehung des hellgrüne "Zeigers" fängt alles wieder von vorne an
(... wobei hier mal davon abgesehen sei, dass
der hellgrüne Zeiger sich bei der Drehung auch noch verformt, also z.B. mal so  und mal
so
und mal
so  aussieht):
aussieht):

Um also evtl. weitere Regeln zu erkennen, reicht es, sich einen einzigen Durchgang anzusehen.
Nun hat
 zwei
entscheidende Nachteile:
zwei
entscheidende Nachteile:

Wenn wir dabei die weißen Flächen 3 als 5 Hintergrund betrachten, bleiben immer noch die drei Flächen x1x, x2x und x4x übrig.
Zu 1., dass also die Veränderungen viel zu schnell ablaufen, um darin eventuelle Regeln erkennen zu können:
glücklicherweise gibt es heutzutage computertechnische Möglichkeiten, die schnelle Abfolge zu verlangsamen oder gar völlig zum Stillstand zu bringen:

Weil schon die ursprüngliche Datei

aus
(wenn auch fürs Auge kaum unterscheidbaren)
statischen Einzelbildern bestand, wird dies in der Verlangsamung noch viel deutlicher.
(aus Platzgründen verkleinert):




































































(Es sei erstmal dahingestellt, ob und, wenn ja, wo diese Aufteilung in Einzelbilder einem bei der Suche nach regel[!]mäßigen Veränderungen helfen kann.)
Zu 2., also den drei Flächen 
(die sich allerdings im Laufe der Zeit kontinuierlich [und doch periodisch] verändern und teilweise für kurze Zeit auch gar nicht sichtbar sind):
Die Flächen x1x und x4x sind zu keinem Zeitpunkt miteinander verbunden
(genauer: sie sind höchstens mal in Einzelpunkten verbunden)
und können deshalb dieselbe Farbe haben.
Um nicht alle drei Flächen x1x, x2x und x4x gleichzeitig beobachten zu müssen und dadurch heillos überfordert zu sein, betrachten wir die drei sich verändernden Flächen getrennt voneinander:
 |
 |
 |
||||
| 1 | 2 | 4 |
Durch die drei getrennten Darstellungen wird immerhin schonmal bzw. jetzt wohl endgültig klar:
(und löscht sogar mal x1x und mal x4x kurzzeitig aus, als wenn er sie überdecken würde).
Wenn man
 mit einer
Schulklasse durchnehmen würde, könnte die drei Flächenverwandlungen
mit einer
Schulklasse durchnehmen würde, könnte die drei Flächenverwandlungen
 |
 |
 |
||||
| 1 | 2 | 4 |
an drei Schülergruppen vergeben, die sich dann jeweils mit einer einzigen Flächenverwandlung beschäftigen würden.
Das sei hier aus Zeit- und Platzgründen nur anhand der
Verwandlung der Fläche x1x
, also
 ,
weiter verfolgt.
,
weiter verfolgt.
Dazu zerlegen wir auch diesen Film wieder in Einzelbilder:



































































Diese Abfolge suchen wir nun nach (Teil-)Sequenzen ähnlicher Figuren ab
(wobei "ähnlich" hier im alltagssprachlichen, nicht im mathematischen Sinne gemeint ist).
Als solche Sequenzen ergeben sich z.B.



































































Wieder zu Filmchen zusammengesetzt ergeben sich damit
(jetzt wieder in Originalgröße und daher besser erkennbar):
A.  B.
B.
 C.
C.

 E.
E.


Damit mögen die Verwandlungen der Fläche x1x halbwegs verstanden sein
(und analog wäre das auch für die Flächen x2x und x4x möglich).
Aber weil eben nur die Einzelfläche x1x betrachtet wurde, bleibt bislang völlig unklar,
wie sich die drei teilweise berührenden Einzelflächen x1x, x2x und x4x zueinander verhalten
und wie sich überhaupt erst durch dieses
Zusammenspiel der (schöne) Gesamteffekt
 ergibt.
ergibt.
Um diesem Zusammenspiel der drei Flächen x1x, x2x und x4x immerhin schonmal ansatzweise auf die Schliche zu kommen, soll nun erstmal versucht werden, das Zusammenspiel der zwei Flächen x1x und x2x zu verstehen, also

Dabei habe ich schonmal die Berührungsstrecken der beiden Formen x1x und x2x rot markiert.
Da aber auch
 noch zu
unübersichtlich ist, jetzt mal nur die
Berührungsstrecken:
noch zu
unübersichtlich ist, jetzt mal nur die
Berührungsstrecken:

Nun hat zwar auch diese vollständige Reduktion ihren ästhetischen Reiz, und es sind auch wieder gewisse Regelmäßigkeiten erkennbar, nämlich z.B. eine sich abwärts bewegende Strecke:
 .
.
Aber das setzt sich für mich doch nicht zu einem
verständlichen Gesamtbild zusammen, weshalb für mich
 nach wie vor weitgehend unverstanden bleibt.
nach wie vor weitgehend unverstanden bleibt.
(Falls es überhaupt jemals jemanden gibt, der diesen Text liest,
und wenn er einen entscheidenden Tipp zum Gesamtverständnis von
 hat, bitte ich ihn, mir diesen Tipp mitzuteilen.)
hat, bitte ich ihn, mir diesen Tipp mitzuteilen.)
Wenn aber schon mir das Gesamtverständnis von
 fehlt,
sollte ich dann nicht auch den Versuch unterlassen,
fehlt,
sollte ich dann nicht auch den Versuch unterlassen,
 mit
Schülern durchzunehmen?!
mit
Schülern durchzunehmen?!
Anders gefragt: darf man im Mathematikunterricht Probleme durchnehmen, die
(„sogar“ für den Lehrer, allemal aber für die Schüler)
nicht vollständig lösbar sind
(hier sei mal von der vermutlich geringen Wahrscheinlichkeit abgesehen, dass vielleicht mal ein Schüler mehr sieht als der Lehrer)?
Der übliche Mathematikunterricht gibt auf diese Frage implizit eine eindeutige Antwort: „Nein, darf man nicht!“
Wie aber von mir in
 dargelegt: „Ja, darf man doch. Mehr noch: sollte man sogar (ab und
zu)!“,
dargelegt: „Ja, darf man doch. Mehr noch: sollte man sogar (ab und
zu)!“,
und zwar
Was aber können die Schüler (überhaupt) bei der Untersuchung von
 lernen,
wenn sie kein Gesamtverständnis erreichen???:
lernen,
wenn sie kein Gesamtverständnis erreichen???:
 ,
,


(wobei die Umformungen weit über
Kongruenz- und Ähnlichkeitsabbildungen hinausgehen, bei denen die grundsätzliche
Form immer erhalten bleibt

 ) ;
) ;
(z.B. die Flächen x1x,
x2x
und x4x
oder  )
)
(z.B.
 ):
):
(zitiert nach
 )
)
... und das alles ohne Fachbegriffe, Konstruktionen und Rechnungen!
(Nebenbei: eine Formumwandlung wie z.B.
 lässt sich auch
halbwegs tun, wenn man ein Anfangsdreieck aus Gummituch benutzt
lässt sich auch
halbwegs tun, wenn man ein Anfangsdreieck aus Gummituch benutzt
[womit wir schon fast in der Topologie sind]:

Insgesamt also:

"halbwegs", weil bei einem Gummituch Einbuchtungen entstehen: )
)