die schönsten Gleichungen aller Zeiten

 

vgl. auch

"Eine ordentliche Gleichung ist [...] nicht nur eine Rechenformel und auch nicht nur eine Waage, die die Gleichheit zweier Objekte bestätigt, deren Identität man vorher schon vermutet hat. Vielmehr begannen die Wissenschaftler [...], das Gleichheitszeichen (=) als eine Art Teleskop für neue Ideen zu nutzen, als Hilfsmittel, um auf neue, ungeahnte Gebiete aufmerksam zu machen." (David Bodanis)

Es ist unglaublich, aber Mathematik kann schön sein (vgl. ), ja, sogar simpel-abgenagte Gleichungen können schön sein:

1. (und das ist hier das Wichtigste), weil sie so elegant einfach sind, d.h. mit wenigen Zeichen eine ganze Welt zusammenbringen können;

2. rein äußerlich: wir werden noch sehen, dass sich der „Satz des Pythagoras“ einfach gut anhört, und auch gewisse mathematische Symbole wie z.B. ∫ oder ∑ sind einfach elegant (weil z.B. symmetrisch).

Schönheit ist vielleicht das entscheidende Kriterium für Mathematik und Naturwissenschaft (vgl. John D. Barrow: Der kosmische Schnitt; Die Naturgesetze des ästhetischen).

Die im folgenden angeführten Gleichungen haben allerdings noch eine weitere Besonderheit: alle fünf sind - wie man auch leicht an den Geistesgrößen erkennt, die dahinter stecken - zentrale Meilensteine der Mathematik- und Naturwissenschafts- und Geistes- bzw. Kulturgeschichte, ja, anhand dieser fünf Gleichungen ließe sich fast die gesamte Mathematik- und Naturwissenschaftsgeschichte (und damit auch das ) klar machen.

jede Wette:

man kann über zentral wichtige mathematische Gedanken (also auch den Gral der Mathematik, nämlich Beweise!) sehr wohl begeisternd und anschaulich sprechen, auch wenn die Beweise für einen Laien teilweise drei Nummern zu hoch sind - und deshalb im folgenden nicht gegeben werden. Immerhin drücke ich mich nicht - wie viele populärwissenschaftliche Bücher - aus falscher Scham um das, was Mathematik doch vor allem ausmacht: Gleichungen und mathematische Symbole. "Sowas" "geht" - neben aller notwendigen und unvermeidlich langweiligen Routine - immer mal wieder auch schon z.B. in einer 5. oder 9. Klasse, ja, die SchülerInnen haben auf solch weitere Perspektiven ein Recht, und eine Mathematik ohne sowas ist sträflich abgenagt, also gar keine Mathematik. Und ich glaube auch fest, dass man ab und zu für solch abstrakte (also eigentliche) Mathematik, bei der von schnöden Anwendungen und Alltagsbezug kaum die Rede ist, begeistern kann.

---

a² + b² = c² 

ist der berühmte (allerdings auch gerade deshalb gründlich verhasste) „Satz des Pythagoras“.

Man sollte nur endlich mal dringend seine Bedeutung bedenken:

1. ist dieser Satz inzwischen auch schon erstaunliche 2600 Jahre alt;

2. wird mit ihm (erstaunlicherweise) zum ersten Mal ein allgemeingültiger mathematischer Sachverhalt allgemein (für ausnahmslos alle rechtwinkligen Dreiecke) bewiesen: ägypter und Babylonier haben diesen Satz auch schon gekannt bzw. schlichtweg angewandt, aber nicht allgemein beweisen können (bzw. für solch einen Beweis auch keine Notwendigkeit gesehen);

3. ist es doch wahrhaft grenzenlos erstaunlich, dass dieser Satz für eben ausnahmslos alle rechtwinkligen Dreiecke (und nur für die!) gilt;

4. nochmals erstaunlicher ist die Abstraktion und damit die Erfindung der Theorie: denn wirklich rechtwinklige Dreiecke gibt es ja niemals in natura, sondern nur in der menschlichen Phantasie!

5. ist es ebenso erstaunlich, dass mit diesem Satz zum ersten Mal Algebra (Rechnen bzw. Formeln) mit Geometrie (purer Anschauung) verbunden wird;

6. steckt hinter diesem Satz die gesamte (und bis heute wirksame!) Zahlenmystik des Pythagoras: dass Gott die Welt nach mathematischen Formeln erschaffen habe, ja, ein Mathematiker sei; säkularisiert gesagt - und das ist ja keineswegs selbstverständlich, darauf beruht aber all unsere Naturwissenschaft und Technik heute -, dass die Welt nach mathematisch einsehbaren Gesetzen funktioniere;

7. ist es ebenso erstaunlich, dass es für diesen Satz unzählige ganzzahlige Beispiele gibt,

also z.B. 3² + 4² = 5² oder 12² + 35² = 37²

^{(solche Dreierkombinationen ganzer Zahlen nennt man "pythagoräische Zahlentrippel"),}

dass es allerdings für höhere Potenzen (bzw. Verallgemeinerungen, nach denen Mathematiker immer suchen), also z.B.

              a³ + b³ = c³ und

              a⁴ + b⁴ = c⁴ und überhaupt

              aⁿ + bⁿ = cⁿ

(wobei „n“ irgendeine ganze Zahl, also z.B. 3 oder 7 oder 172345 ist)

keine einzige ganzzahlige Lösung gibt

(d.h., dass man für a, b und c niemals ganze Zahlen eingeben kann, so dass die Gleichung aⁿ + bⁿ = cⁿ aufgeht).

Dass das in höheren Dimensionen als 2 unmöglich ist, ist ja gerade die berühmte – und inzwischen durch Andrew Wiles bewiesene – Vermutung von Fermat:

(vgl.   )

Der Satz des Pythagoras hat noch eine andere, mindestens ebenso wichtige literarisch-sprachlich-lautliche Schönheit: er funktioniert nach einem ungeheuer suggestiven Rhythmus:

a       ²         +   b      ²                =     c         ²

a Quadrat plus b Quadrat gleich c Quadrat

/    -     -  |   _  | /      -     -  |      _   | /      -   -

D.h. er besteht aus schmissigen Daktylen ( / - - ), also  ³/₄-Walzertakten, was seine Merkbarkeit, aber auch suggestive „Richtigkeit“ ungemein erhöht:

---

bzw., wenn's einem so lieber ist, weil da das π deutlicher hervortritt,

Um zu verstehen, wie aberwitzig diese Gleichung ist, muss man sich vorerst klar machen, was eigentlich ist:

die berühmte "Kreiszahl" ≈ 3,141592654.

"Eigentlich" ist diese Kreiszahl ja was sehr Einfaches: wenn man einen Kreis mit dem simplen Durchmesser 1 hat, so ist sein sich ebenso simpel ergebender Umfang .

Nur ist halt die ziemlich schräge Zahl 3,141592654.

(Das ist leider bzw. erstaunlicherweise oft so in der Mathematik: oftmals hat man nur die Wahl zwischen

• einem einfachen Anfang und einem schwierigen Ende

• oder umgekehrt.

Z.B. enthält das simple Quadrat mit der Seitenlänge 1 eine ganz simple Linie, nämlich die Diagonale, die aber die scheußliche Länge ≈ 1,4142135 hat; wenn man hingegen umgekehrt für ein anderes Quadrat die scheußliche Seitenlänge ≈ 1,4142135 wählt, so ist seine Fläche sehr simpel 2.)

Mit ist es aber noch erheblich vertraxter:

ist eben nur ungefähr 3,141592654, d.h. die 4 am Ende bestimmt zwar (immerhin) auf ein Milliardenstel genau

(und ein normaler Mensch will's ja gar nicht so genau wissen; ein Mathematiker aber schon!),

aber damit ist die Dezimaldarstellung noch lange nicht zu Ende.

Vielmehr lässt sich beweisen, dass 

1. noch unendlich viele Stellen hinter dem Komma kommen,

(d.h., selbst wenn man noch so viele Nachkommastellen hat, ist ein Gleichheitszeichen zwischen und seiner Dezimaldarstellungmathematisch IMMER FALSCH; denn ein Gleichheitszeichen - solche Korinthenkacker und Pfennigfuchser sind die Mathematiker nunmal -  ist in der Mathematik NUR bei ABSOLUTER Gleichheit erlaubt),

2. diese Stellen auch nie (wie z.B. in 1, 234 234 234 ...) periodisch werden

(genau das aber ist irrwitzig und doch der Inbegriff von Mathematik [und was sie von sämtlichen anderen Wissenschaften unterscheidet]: dass man in einem endlichen Beweis etwas über Unendlichkeit aussagen kann).

Aus a. und b. folgt für einen Mathematiker:

ist "irrational"

(anders gesagt: ist nicht - was unten noch wichtig werden wird - als EIN Bruch aus irgendwelchen ganzen Zahlen darstellbar),

und dieses "irrational" nehme man doch bittschön mal entdeckungsgeschichtlich im Wortsinne: "unvernünftig", "gehirnausrenkend".

(Ausgerechnet Mathematiker haben immer - und zwar aus ebenso guten wie subversiv anhaltenden Gründen - jeweils den nächsten noch unverstandenen Sachverhalt als Blödsinn eingestuft; die nächsten Kandidaten nach den

• irrationalen

[laut Duden - ausgerechnet in der Mathematik! - durch logisches Denken nicht fassbaren]

waren eben

• die transzendenten

[laut Duden die Grenzen der Erfahrung und der sinnlich erkennbaren Welt überschreitenden]

und dann

• die imaginären

[laut Duden nur scheinbaren, in der Einbildung vorhandenen, unwirklichen]

bzw.

• bzw. die komplexen

[laut Duden verwickeltenen, verflochtenen, verzweigten, zusammengesetzten, beziehungsreichen]

Zahlen.)

geht also in der Dezimaldarstellung hinterm Komma unendlich und - mehr noch - völlig chaotisch (unvorhersehbar) weiter.

(Nur nebenbei sei erwähnt, dass π  sogar zu einer besonders scheußlichen [oder hübschen] Unterfamilie der irrationalen, nämlich zu den o.g. "transzendenten" Zahlen gehört.)

Aus all dem folgt zweierlei:

1. noch kein Mensch hat die Dezimaldarstellung von 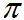ganz gesehen, ja, das ist wegen der unendlich vielen Nachkommastellen grundsätzlich ausgeschlossen, wird also auch in Zukunft (und auch mit allerbesten Computern) nie geschehen

(schon das allein scheint mir bemerkenswert genug: man kann tatsächlich beweisen, dass es nie gelingen wird);

2. keiner (da sind Mathematiker auch nicht schlauer als Laien) hat auch nur den blassesten Schimmer, wie sie "ganz weit hinten" weitergeht.   

(Weil das prinzipiell unmöglich ist, kann man sich auch streiten, ob die "Freunde der Zahl pi", bei denen man erst aufgenommen wird, wenn man die ersten hundert Nachkommastellen von auswendig kennt, Witzbolde oder aber arme Idioten sind.

Nun zeigen sie auf ihrer Homepage immerhin herrliche Selbstironie, wissen also ganz genau, dass sie wie Sisyphos prinzipiell aussichtslose Arbeit [aber welche Arbeit ist das nicht?] leisten.

Ein richtiger Mathematiker hat sowieso nicht den mindesten Respekt vor Rechenkünstlern, ja, Rechnen [also der Umgang mit Einzelfällen] ist sowieso unter der Würde eines echten Mathematikers, bzw. dazu ist er einfach viel zu faul. Und Rechnen kann ja jeder Idiot, nämlich sogar Computer.)

Da fragt sich doch, wie man denn überhaupt Nachkommastellen von bekommen hat, also z.B. eben (s.o.) 3,141592654.

Nun kann man natürlich oben genannten Kreis mit dem Durchmesser 1 (m) bauen und dann den Umfang ausmessen. Aber der wird doch höchstens auf etwa einen Millimeter genau zu messen sein, womit sich ≈ 3,141 ergibt.

Und damit nun sind wir bei der irrwitzigen Gleichung 

bzw.

,

die Leibniz

entdeckt hat.

(Keine Ahnung, wie er drauf gekommen ist; und ich vermute sogar, dass ich den Beweis vielleicht in allen Einzelschritten verstehen würde, er mir aber - wie so oft in der Mathematik - gerade nicht anschaulich zeigen würde, weshalb so etwas Einfaches wie die rechte Seite der Gleichung "rauskommt";
dabei ist es wegen des Konstruktionsprinzips natürlich klar selbstverständlich, dass die Reihe rechts gegen genau eine Zahl konvergiert;

1. werden die Sprünge immer kleiner, ja, unendlich klein;

2. wechseln sich die Sprünge jeweils ab: hoch [+] und runter [-]

3. ist der folgende Sprung immer kleiner als der vorherige.

Man kann sich das vorstellen wie eine sich verengende Trompetenöffnung (nur dass der Ton nicht aus ihr raus kommt, sondern in sie rein fällt):

Aber es ist noch lange nicht ausgemacht, dass diese eine Zahl ausgerechnet ist.)

Das wahrhaft Umwerfende an der Gleichung 

 

ist doch nun aber, dass

• auf der linken Seite der Gleichung mit der Zahl 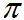, wie oben gezeigt, etwas ungeheuerlich Kompliziertes steht,

• auf der rechten Seite aber eine Kombination aus ganz simplen Brüchen mit hübsch regelmäßig abwechselnden Vorzeichen,

• beide Seiten dennoch (hoffentlich kann man noch staunen!) durch das Gleichheitszeichen fest zusammengeschweißt sind.

Hier zu staunen, heißt für mich, sich fassungslos zu fragen:

• Warum nur - hübsch nacheinander - ungerade Nenner (aber der Zähler 1 und die gerade Zahl 4 davor)? Und warum so hübsch abwechselnd "plus" und "minus"?

• Woher wusste die Kombination der simplen Brüche auf der rechten Seite, dass sie exakt gleich der linken Seite, also die fürchterlich komplizierte Zahl 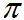sein sollte?

• Und ist es nicht ein extrem unwahrscheinlicher Zufall, dass ausgerechnet diese beiden Ehepartner zusammen gefunden haben? 

Die Reihe kommt einem fast vor wie ein unendliche "Schlange" mit Eigenleben:

Mit der Gleichung

kann man nun also tatsächlich massenhaft Nachkommastellen von  berechnen, denn mit (zudem noch so einfachen) Brüchen rechnen kann ja wohl jeder oder zumindest jeder Taschenrechner.

Kann man wirklich? Die Crux sind doch die unscheinbaren Pünktchen ganz rechts. Die Summe geht endlos so weiter, es folgen - wenn auch in klarer Regel - Brüche auf Brüche. Und ich kann genauso wenig alle (unendlich viele!) Brüche (auf der rechten Seite) aufaddieren wie ich die unendlich vielen Nachkommastellen von (auf der linken Seite)aufzählen kann.

Wir scheinen also Teufel mit Beelzebub ausgetrieben zu haben bzw. vom Regen in die Traufe gekommen zu sein: wir haben nur die eine unmögliche Unendlichkeit durch die andere ersetzt.

Dennoch hat die Gleichung einen enormen Vorteil:

• während ich über die linke Seite rein gar nichts sagen kann,

• kann ich rechts immerhin bis zu einem bestimmten Bruch (z.B. dem 1000sten) aufaddieren. Und nach Leibniz wissen wir: wir kommen immer näher (sogar unendlich nahe) an "die Große Unbekannte" 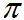heran, wir erhalten tatsächlich immer mehr richtige Nachkommastellen.

(Dabei ist allerdings eins klar: weil jede noch so lange, aber endliche Bruchsumme rechts wieder ein Bruch, also rational ist, werden wir nie exakt erreichen, weil eben irrational ist;
auf obige Definition irrationaler Zahlen zurückkommend: ist als irrationale Zahl auch jetzt noch immer nicht als EIN Bruch aus irgendwelchen ganzen Zahlen darstellbar, sondern nur durch eine Summe unendlich vieler Brüche aus ganzen Zahlen annäherbar.)

Es ergeben sich zuguterletzt zwei Probleme:

1. ist 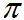leider nur über solch unendliche Reihen wie auf der rechten Seite anzunähern, es gibt nachweislich leider keinen anderen, einfacheren Weg;

2. die rechte Seite geht sehr langsam gegen 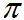, für zwanzig richtige Nachkommastellen muss man z.B. - wie schon Newton eingewandt hat - abermillionen Brüche addieren.

Wieder in Analogie zur Trompetenöffnung: sie ist sehr lang gestreckt und wird nur langsam enger: 

            

Die schlechte Konvergenz der Leibniz-Reihe liegt darin begründet, dass die jeweils dazukommenden Summanden immer auch inetwa den Fehler bestimmen, also z.B. der Fehler nach dem 5000sten Summanden etwa 1/(2 mal 5000) = 1/10000 ist.

Z.B. konvergiert das Heronverfahren (allerdings nicht für , sondern für die ) erheblich schneller.
In Analogie zur Trompetenöffnung: sie ist sehr kurz und wird viel schneller eng:

                

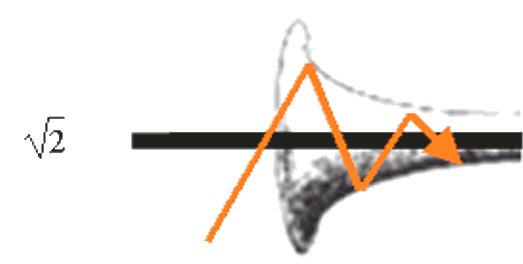
Man muss allerdings auch bedenken, dass die Leibniz-Reihe gar nicht geschaffen wurde, um Nachkommastellen von zu berechnen. Sondern es ging einzig und allein darum zu zeigen, dass es tatsächlich eine Reihe gibt, die annähert.

Nun sind inzwischen zwar bessere, sich schneller an annähernde Reihen als die Leibniz-Reihe entdeckt worden, aber das Grundproblem (weil es eben alles unendliche Reihen [und unendlich Summen nennt man ja gerade "Reihen"] sind) bleibt. 

(Computer können heute die irrwitzig langen Teilsummen aus Brüchen zwar rasend schnell berechnen, aber bei der Bestimmung von auf eine Milliarde Nachkommastellen genau kommt auch der größte Computer der Welt ins Schwitzen, bzw. dafür braucht auch er ewig lange.)

Der mit Computern aufgestellte Rekord für steht heute (7.12.2000) angeblich bei 206 158 430 000 richtigen Nachkommastellen. Davon als kleines Schmankerl nur 

≈ 3,1415926535897932384626433832795028841971693993751058209749445923078...

(also eine nachweisbar sinn- bzw. regellose Folge von Ziffern; genau damit tun wir Menschen [also auch Mathematiker!] uns schwer, das können wir nicht akzeptieren, ja, empfinden wir fast als Demütigung: wir sind evolutionär darauf getrimmt [und könnten ohne das auch gar nicht überleben], Ordnung zu sehen bzw. notfalls, falls eben keine vorliegt, sie hinein zu sehen).

Da ist mir das knackig kurze und zudem so ästhetisch geschwungene Symbol

doch erheblich lieber, ja, mir scheint sogar, dass ein Großteil der Faszination, die von ausgeht, von der Form und archaischen Fremdheit dieses Symbols herrührt.

(und z.B. auch ist herrlich schnuckelig im Vergleich mit seiner ekligen Dezimalschreibweise 1,4142135 und so weiter und so ewig und so unvorhersehbar und so fort;
und fast das Wichtigste - worüber sich aber kaum jemand mehr wundert - an der   ist ihr Name, nämlich "Wurzel": vgl. im Duden "Wurzeln schlagen; seinen Ursprung in etwas haben": entgegen aller Entdeckungsgeschichte sind da die irrationalen Zahlen der  geheimnisumwitterte Ursprung der ganzen Zahlen bzw. ist sozusagen Metaphysik der Urgrund aller Physik;
auch mathematische [und naturwissenschaftliche] Bezeichnungen/Definitionen sind ja nur scheinbar willkürlich, bzw. sie transportieren fast  immer auch andere, unliebsame, umgangssprachliche, erkenntnisfördernde, aber auch erkenntnishemmende Assoziationen)

---

e ⁱ + 1 = 0

Ein Nichtmathematiker wird sich bei dieser von solch einem Jahrtausendgenie wie eben Euler

bewiesenen Gleichung allemal fragen, was solch ein Quatsch (solch eine Kombination aus unverständlichen Zeichen) denn eigentlich soll.

für einen Mathematiker hingegen ist diese Gleichung geradezu „der Orgasmus der Mathematik“:

wie konnte es denn möglich sein, in einer einzigen Formel sämtliche zentralen Natur- und Mathematikkonstanten zusammen zu bringen?:

1. die irrationale (!) Eulersche Zahl (der Maßstab aller natürlichen Vermehrung) e ≈ 2,718281828 (nach dem Komma unendlich, aber nicht periodisch, also irrational)

Eli Maor: Die Zahl e - Geschichte und Geschichten; Birkhäuser

2. die Erfindung der sogenannten imaginären bzw. komplexen Zahlen, also die Zahl i, für die i² = -1 gilt,

3. die schon oben erwähnte irrationale Kreiszahl 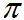≈ 3,141592654

	David Blatner: ; Magie einer Zahl; Rowohlt
	Jörg Arndt, Christoph Haenel: Pi; Algorithmen, Computer, Arithmetik; Mit CD-ROM; Springer

4. die Urzahl 1,

5. den Geniestreich der Inder, die Zahl 0

	Charles Seife: Zwilling der Unendlichkeit; Eine Biographie der Zahl Null; Berlin Verlag
	Robert Kaplan: Die Geschichte der Null; campus
	Brian Rotman: Die Null und das Nichts; Eine Semiotik des Nullpunkts; Kadmos

Nebenbei: man muss gar nicht verstehen, weshalb die Formel aufgeht - und kann sie doch bewundern.

---

s = ¹/2 g t²

(wobei s der zurückgelegte Weg eines fallenden Körpers ist, g die sogenannte „Gravitationskonstante“ [auf der Erde etwa 10] und t die Zeit seit Beginn des Falls)

also die Beschreibung des freien Falls eines Körpers:

1. ist das die allererste, meines Wissens erstmals von Newton

aufgestellte mathematische Formel, die auch auf Physik anwendbar ist;

2. ist es nicht grenzenlos erstaunlich, dass man mittels dieser Gleichung Zeit und Raum (zurückgelegten Weg) in Verbindung bringen kann?

(Nachtigall, ick hör dir trapsen: da ist doch schon "versehentlich" Einsteins Relativitätstheorie [s.u.], die ja gerade eine Einheit von Zeit und Raum suggeriert, impliziert)

3. ist es nicht um so erstaunlicher, dass sich die Natur überhaupt durch simple mathematische Gesetze erfassen lässt, ja, dass sie geradezu nach ihnen konstruiert zu sein scheint?

4. ist es mindestens ebenso erstaunlich, dass Galilei

erkannt hat, dass (entgegen aller Anschauung) in solch einer Formel das Gewicht des fallenden Körpers keine Rolle spielt, also gar nicht vorkommt?

(es widerspricht allem durchaus "gesunden" Menschenverstand, dass zwei verschieden schwere Körper [z.B. eine Daunenfeder und ein Betonklotz] gleich schnell fallen; tun sie ja auch nicht! - sondern nur im Vakuum, das es im Weltall nirgends vollkommen gibt) 

Mit solcher Abstraktion vom Gewicht und der simplen Anschauung hat Galilei seinen absoluten Geniestreich begangen (und gleichzeitig die Schizophrenie alles heutigen Bewusstseins eingeleitet: dass wir "wissen", was wir nicht wahrnehmen können).

Vgl. allerdings auch  .

5. so richtig mathematisch schön, d.h. einfach wird diese Gleichung allerdings erst, wenn man sie zu s ' = gt ableitet

(wobei – mathematisch so wunderbar einfach zusammenhängend – diese Ableitung s' gleich der Momentangeschwindigkeit v des ja ständig beschleunigt fallenden Körpers ist und diese Momentangeschwindigkeit eben besonders einfach linear zunimmt: wenn die Zeit doppelt [dreimal ...] so lang ist, ist auch die Geschwindigkeit doppelt [dreimal ...] so groß).

---

E = m • c²

(wobei E die Energie ist, die in einer Masse steckt, m die Masse und c die Lichtgeschwindigkeit [also ≈ 300 000km in der Sekunde])

vgl. auch

Wie so oft ist der Originaltitel viel besser:
"E = mc². A Biography [!!!] of the World's Most Famous Equitation [Gleichung]"

An dieser von Einstein aufgestellten Gleichung ist dreierlei so umwerfend bis geradezu gehirnausrenkend:

1. , dass Masse und Energie im Prinzip dasselbe sind, nur verschiedene Zustandsformen so wie etwa Wasser und Eis,

2. , dass in der popeligsten Masse eine ungeheure Energie steckt

(um die Energie zu berechnen, wird die Masse ja mit dem alles nochmals aufblühenden Quadrat einer riesigen Zahl, nämlich der Lichtgeschwindigkeit, multipliziert),

3. , dass sich das alles nach so einer simplen Gleichung verhält.

Das Problem ist halt nur:

1. : wie schafft man es, diese riesige Energie eine Masse freizusetzen? Z.B. durch Kernfusion wie in der Sonne!

2. funktioniert nach genau dieser Gleichung - was nicht mal Einstein vorausgesehen hat, als er die abstrakte Gleichung hatte - eben auch die Atombombe!

(Ein kleines Schmankerl am Rande: Einsteins berühmteste Formel ist gar nicht von Einstein, sondern erst Max Planck hat sie mit zusätzlichen Mitteln aufstellen können.)

---

Schönheit ist "relativ"

(die größte und fast schon gefährliche Banalität ist, dass laut Einsteins Relativitätstheorie "alles" relativ sei; eben das hat er ja gerade nicht gesagt: die Basis seiner Theorie, nämlich die Lichtgeschwindigkeit, ist ebenso wenig relativ wie - zumindest laut seiner Theorie - die Gültigkeit der Naturgesetze im gesamten Universum).

Bzw. vielleicht kann manchmal eben doch mehr Schönheit empfinden, wer mehr weiß

(wer also z.B. Substrukturen eines Romans erkennt, die einem anderen verschlossen bleiben).

Z.B. bleibt mir die Schönheit von

(im Original sogar "God's Equation"; dementsprechend heißt auch in der deutschen Ausgabe das letzte Kapitel "Gottes Gleichung"),

also von

R_μν - λg_μνR = - 8 GT_μν

bzw. mit der kosmologischen Konstante λ

R_μν - λg_μνR - λg_μν= - 8 GT_μν

_{völlig verschlossen.}

("Dabei ist R_μν der Ricci-Tensor, R seine Spur, λ die kosmologische Konstante, g_μν das Abstandsmaß - der metrische Tensor der Geometrie des Raums - G Newtons Gravitationskonstante und T_μν der Tensor, der die Eigenschaften von Energie, Impuls und Materie beschreibt [...]"
Alle Klarheiten beseitigt?)

_{Ich kann zwar zusagen "kognitiv" nachvollziehen:}

• "Die Gleichung besaß ein solches Erklärungsvermögen, verriet so viel Einsicht in die Naturgesetze, von denen vor Einstein niemand etwas geahnt hatte, dass sie in ihrer Hellsichtigkeit geradezu unheimlich erschien. In jedem Jahrzehnt seit ihrer Geburt hat die Gleichung ihre Wahrheit immer wieder auf unerwartete Weise unter Beweis gestellt. Wie konnte ein einziger Mensch die Geheimnisse unseres Universums so gründlich verstehen?"

• "Lösungen dieser Gleichung haben uns zu der Entdeckung von phantastischen Phänomenen geführt - Phänomenen, die die Gleichungen vorhersagen. Dazu gehören Gravitationswellen, die Wölbung des Raums, das Phänomen des »Frame-Draggings«, wo die Raumzeit von der Rotation eines massereichen Körpers mitgerissen wird, nicht zu reden von dem Perihelproblem, der Gravitations-Rotverschiebung und der Lichtablenkung."
  (beides Zitate aus o.g. Buch)

_{Aber die Gleichung hat für mich}

• _{keinen Rhythmus,}

• _{keine optische Schönheit,}

• _{und wegen mangelnder Kenntnisse zur sogenannten "Tensorrechnung" kann ich schon gar nicht durch sie hindurch auf die Schönheit der kosmischen Wirklichkeit dahinter schauen. Bzw. ich erkenne die Schönheit der kosmischen Wirklichkeit, die mir populärwissenschaftliche Bücher wie das von Azcel durchaus vermitteln, nicht in der Gleichung wieder. Ich kann nur respektieren, was Aczel behauptet:}

_{"Einsteins Feldgleichung der Gravitation ist mathematisch außerordentlich elegant. Darum war Einstein schon fest von der Richtigkeit seiner Gleichung überzeugt, als noch kein experimenteller Beweis für die allgemeine Relativitätstheorie vorlag, und deshalb hat er später auf die Frage, was er getan hätte, wenn sich ein solcher Beweis nicht gefunden hätte, geantwortet: »Da könnte mir halt der liebe Gott [!] Leid tun. Die Theorie stimmt doch.«"}

_{Bzw. ich kann es nur analogisierend nachvollziehen:}

Gleichungen können so mathematisch schön sein, dass sie geradezu richtig sein müssen.

---

Zuguterletzt finde ich es grenzenlos erstaunlich, dass sich einerseits die Mathematik, andererseits die „Welt“ ÜBERHAUPT in Gleichungen erfassen lässt,

dass also überhaupt ein  = möglich ist.

für mich ist es eben nicht selbstverständlich, dass

• sich rechtwinklige Dreiecke nach dem Satz des Pythagoras richten,

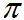• laut 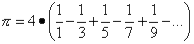 durch simple Brüche darstellbar und annäherbar ist,

• e, i, 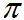und 1 in einem genial einfachen Verhältnis zueinander stehen,

• der freie Fall sich gnädigst dazu herablässt, nach einer relativ simplen Formel zu verlaufen,

• E und m überhaupt zusammenhängen, ja, dasselbe sind.

Was für Meilensteine der Mathematik, dass man dennoch drauf gekommen ist!

Jadoch, es wird Zeit, noch und wieder voller Ehrfurcht und Andacht über Mathematik  staunen zu können!

- und ich schäme mich keineswegs solch eines feierlichen bis geradezu religiösen Tons.