oder zu viele Tasten
gnadenlos systematisch
oder zu viele Tasten ![]()
In der Mathematik folgt vieles gnadenlos nach einander (und aus einander), z. B.
nach (a + b )2 = (a + b) (a + b) = a2 + 2ab + b2 ( + , + )
und (a - b )2 = (a - b) (a - b) = a2 - 2ab + b2 ( - , - )
unweigerlich (a + b) (a - b) = a2 - b2 ( + , - )
in der Dreieckslehre
nach der Verbindung dreier Winkel (w,w,w: Winkelsumme 1800)
und der Verbindung dreier Seiten (s,s,s; Satzgruppe des Pythagoras)
dann endlich die Verbindung eines Winkels mit zwei Seiten (w,s,s; Trigonometrie).
In beiden Fällen werden also nacheinander alle möglichen Kombinationen
(erst "reinrassig" [ + , + , - , - / w,w,w, s,s,s],
dann "gemischtrassig" [ + , - / w, s,s ])
durchgespielt
Die Gnadenlosigkeit zeigt sich dabei auch in der verzweifelten Suche nach Vollständigkeit. So schreit die Dreieckslehre doch noch nach der einzigen fehlenden Kombinationsmöglichkeit, nämlich "w,w,s".
Ein anderes Beispiel für diese Jagd nach Vollständigkeit ist ![]() :
:
| a + b = c | immer lösbar |
| a2 + b2 = c2 | manchmal lösbar |
| ? | ? |
Eine erste Antwort ist
| a + b = c | immer lösbar |
| a2 + b2 = c2 | manchmal lösbar |
| a3 + b3 = c3 | nie lösbar |
Und noch allgemeiner und nun endlich vollständig (für alle n):
| a + b = c | immer lösbar |
| a2 + b2 = c2 | manchmal lösbar |
| an + bn = cn | nie lösbar für n > 2 |
Manchmal ist allerdings leider nicht "vollständige Vollständigkeit", sondern nur eine Teil-Vollständigkeit erreichbar.
Beispielsweise gilt in der Dreieckslehre
die Verbindung dreier Winkel (w,w,w: Winkelsumme 1800) in tatsächlich allen (ebenen) Dreiecken,
die Verbindung dreier Seiten (s,s,s; Satzgruppe des Pythagoras) leider "nur" in allen rechtwinkligen Dreiecken
die Verbindung eines Winkels mit zwei Seiten (w,s,s; Trigonometrie) ebenfalls leider "nur" in allen rechtwinkligen Dreiecken.
(Aber man weiß sich zu helfen: wenn ein Dreieck nicht rechtwinklig ist, zerlegt man es mittels der Höhe in zwei rechtwinklige Dreiecke, und schon kann man doch die Satzgruppe des Pythagoras bzw. die Trigonometrie anwenden.)
Und selbst im ersten Fall, also bei der Winkelsumme, war die Einschränkung "ebenen" nötig: in Dreiecken beispielsweise auf einer Kugel
gibt es nicht die Winkelsumme 1800 ,
und noch schlimmer: es gibt nichtmal eine (einzige, einheitliche) andere Winkelsumme, sondern unterschiedlichste Winkelsummen (wenn auch immer größer als 1800 ).
Oben hatte ich schon Begriffe benutzt, die das Dilemma schön deutlich machen:
einerseits negative Begriffe wie "gnadenlos" und "verzweifelt",
andererseits "durchgespielt" und damit indirekt den positiven Begriff "spielerisch".
Ich vermute mal, dass sich genau hier die Geister scheiden:
die einen (Nicht-Mathematiker) werden die gnadenlose Systematik als abstoßend empfinden,
die anderen (Mathematiker) haben an ihr meistens ihren unbändigen Spaß, und zwar an dreierlei:
Spaß an einem Automatismus "aus der Sache heraus": wie sich da also - ohne menschliches Zutun - in rein logischer Folgerichtigkeit eins aus dem anderen ergibt,
Spaß an den eigenen Gestaltungsmöglichkeiten,
Spaß daran, wie wunderbar einerseits der Automatismus und andererseits die eigenen Gestaltungsmöglichkeiten zusammen passen.
(Von wegen "meistens": es sei doch unbedingt ergänzt, dass die gnadenlose Folgerichtigkeit [und ebenso gnadenlose Suche nach Vollständigkeit] auch schon den einen oder anderen Mathematiker "in den Wahnsinn" und in Verzweiflung getrieben hat, nämlich dann, wenn ein Problem zeitweise oder bislang überhaupt nicht lösbar war.)
Im üblichen Schulunterricht empfinden die SchülerInnen wohl sehr oft die Gnadenlosigkeit der Systematik, aber wohl allzu selten den Spaß an den eigenen Gestaltungsmöglichkeiten.
Das liegt vermutlich daran, dass die Gnadenlosigkeit meist nur in zwei Formen auftaucht:
als permanente Rechthaberei der Mathematik,
als "Mikro-Gnadenlosigkeit" von Einzelbeweisen.
Was in Schulen vor lauter "Einheitsbrei"
(beispielsweise Termumformungen bis zum Abwinken)
weitgehend fehlt, sind
der Spaß an langfristigen Projekten
und deutlich erkennbare Fortschritte, also auch Anlässe zu Stolz.
Beispiel sei da wieder die Dreieckslehre: wann wird denn mal
in einer 5. Klasse bei w,w,w erwähnt, dass noch s,s,s (9. Klasse) und w,s,s (10. Klasse) fehlen,
in einer 10. Klasse bei w,s,s erwähnt, dass man nun alles (w,w,w / s,s,s / w,s,s) erreicht hat?
Wo wird denn überhaupt mal solche (weitestmögliche) Vollständigkeit explizit als langfristiges Projekt erwähnt?
Ich glaube auch nicht, dass diese langfristige Vollständigkeit "a priori" (wenn man in der 5. Klasse ist) automatisch frustrierend etwa nach dem Motto
"oh Gott, wie viel noch zu tun ist; und das ist doch alles noch unvorstellbar weit weg"
ist. Sondern ich habe es vielfach erlebt, dass die SchülerInnen sehr gespannt auf das waren, was ihnen noch "bevorstand". Nur darf man nicht bloß erwähnen, was später noch kommt, sondern sollte es den SchülerInnen
(etwa nach dem Motto "das ist ja eigentlich was für Große, aber ihr seid ja auch nicht dumm")
schon partiell "zumuten" und sie derart "bei ihrer Ehre packen".
Beispielsweise sollte man bei der Einführung der Brüche (5./6. Klasse) irrationale Zahlen nicht - wie üblich - verschweigen und darf man sie auch nicht bloß erwähnen
(und dann auf die 9. Klasse verweisen, wo sie genauer behandelt werden; das wäre, als würde man einen Krimi nur halb erzählen und dann sagen: "In drei Jahren erzähle ich euch, wer der Mörder ist.").
Sondern man sollte eben auch schon die 5.-/6.-KlässlerInnen mit irrationalen "Schlangen" à la
1, 1 2 3 4 5 6 7 8 9 10 11 12 ...
oder
1, 0 1 00 1 000 1 0000 1 ...
hantieren lassen
(sie tun das ungeheuer gern!).
Und umgekehrt wird mir doch allzu selten "a posteriori" (in der 10. Klasse) der Stolz darauf herausgestellt, dass man nun tatsächlich endlich "alles" erreicht hat, nämlich z.B.
w,w,w / s,s,s / w,s,s,
sämtliche Funktionenklassen, die überhaupt in der Schule vorkommen - und die dann in der Oberstufe "nur" noch genauer untersucht werden.
(Genauer: "Bislang können wir sowas Wichtiges wie das Maximum/Minimum nur - mittels der Scheitelpunktsform - für Parabeln bestimmen; da steht es natürlich noch aus, das auch für alle anderen [uns inzwischen ja bekannten] Funktionenklassen zu können.)
Es müsste also deutlicher werden, dass 10.-KlässlerInnen auch fachlich (mathematisch) ein wichtiges (Zwischen-)Ziel erreicht haben und auch in diesem Sinne einen (mittleren) Schul-Abschluss erhalten.
Ein Beispiel für den Spaß an den eigenen Gestaltungsmöglichkeiten, ja der Gaudi am Rumspielen ist "w,s,s", also die Trigonometrie:
angenommen mal, der Sinus ist schon in all seinen Fassetten eingeführt worden:
| Sinus |
|
|
|
Dabei soll uns hier gar nicht interessieren, wie 1., 2. und 3. zusammen hängen bzw. wie sich 2. und 3. aus 1. ergeben.
Sondern wir spielen einfach mit 1. und 2. herum und entwickeln eine Alternative, die wir dreist "Cosinus" nennen. In logischer Abwandlung des Sinus ergibt sich dann:
| Sinus | Cosinus |
|
|
|
|
|
Wir haben also
in  nur die andere Dreiecksseite als in
nur die andere Dreiecksseite als in  genommen
genommen
und in  (im Vergleich mit
(im Vergleich mit  ) die Gegenkathete durch die Ankathete ersetzt.
) die Gegenkathete durch die Ankathete ersetzt.
Noch kurz sei der Funktionsgraph des Cosinus ergänzt:
| Sinus | Cosinus |
|
|
|
|
|
|
Da wir bisher mit den Verhältnissen  und
und  gespielt hatten, liegt es jetzt nahe, mal nur die Katheten zu kombinieren, also z.B. in der Version
gespielt hatten, liegt es jetzt nahe, mal nur die Katheten zu kombinieren, also z.B. in der Version  . Was sich dabei neu ergibt, nennen wir probeweise mal (und doch mit Hintersinn) "Tangens", und somit erhalten wir:
. Was sich dabei neu ergibt, nennen wir probeweise mal (und doch mit Hintersinn) "Tangens", und somit erhalten wir:
| Sinus | Cosinus | Tangens |
|
| |
|
|
|
|
|
Wie schon gesagt, hatten wir den Namen "Tanges" mit Hintersinn gewählt. "Tangens" ist natürlich von "Tangente" abgeleitet, und dementsprechend zeichnen wir nun an den Einheitskreis eine Tangente.
Weil aber
beim Tangens in  die Gegenkathete genauso im Zähler steht wie beim Sinus, also in
die Gegenkathete genauso im Zähler steht wie beim Sinus, also in  ,
,
und weil der Sinus in  vertikal abgetragen war,
vertikal abgetragen war,
wählen wir nun auch eine vertikale Tangente.

Der Tangens wird nun aber nicht mehr innerhalb des Einheitskreises gemessen, sondern außerhalb auf der Tangente, und damit erhalten wir
(wobei wir zusätzlich auch schon den Funktionsgraph des Tangens ergänzen):
| Sinus | Cosinus | Tangens |
|
|
|
|
|
|
|
|
|
Nun hätten wir statt  aber natürlich genauso gut
aber natürlich genauso gut  wählen könnten - und jetzt rate man mal, wie wir Letzteres nennen: natürlich
wählen könnten - und jetzt rate man mal, wie wir Letzteres nennen: natürlich
(weil jetzt die Ankathete genauso im Zähler steht wie beim COsinus)
COtangens!
Und weil der Cosinus in  horizontal abgetragen wurde, wählen wir jetzt natürlich auch eine horizontale Tangente, auf der wir den Cotangens einzeichnen:
horizontal abgetragen wurde, wählen wir jetzt natürlich auch eine horizontale Tangente, auf der wir den Cotangens einzeichnen:
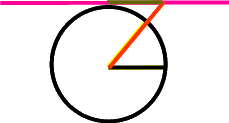
Inkl. Funktionsgraph erhalten wir dann
| Sinus | Cosinus | Tangens | Cotangens |
| ... | ... |
|
|
| ... | ... |
|
|
| ... | ... |
|
|
Die derart erarbeitete Systematik wird noch deutlicher, wenn man folgendermaßen sortiert:
| Sinus | Cosinus | Tangens | Cotangens |
|
|
|
|
|
|
|
|
Oder noch augenfälliger:
| Sinus | Cosinus | Tangens | Cotangens | ||||||||
| | | | | ||||||||
| | | | |
Man sieht, dass wir somit in vielfältiger Kombination alle Möglichkeiten durchgespielt haben.
Nochmals: wir hatten einfach wild draufloskombiniert, aber noch keinerlei Rücksicht darauf genommen, ob sich da auch jeweils 2. und 3. logisch aus den Definitionen (also 1.) ergeben.
Da sei an die verschiedenen Formen von Spaß erinnert, die oben genannt worden waren:
Spaß an einem Automatismus "aus der Sache heraus": wie sich da also - ohne menschliches Zutun - in rein logischer Folgerichtigkeit eins aus dem anderen ergibt,
Spaß an den eigenen Gestaltungsmöglichkeiten,
Spaß daran, wie wunderbar einerseits der Automatismus und andererseits die eigenen Gestaltungsmöglichkeiten zusammen passen.
Und in der Tat lässt sich zeigen, wie jeweils 2. und 3. logisch aus den Definitionen (1.) folgen, dass also laut C. unsere Knobellust (B.) durchaus mit dem mathematischen "Automatismus" (A.) harmoniert, wir also nicht Unsinn erknobelt haben.
Eigentlich war die Einführung des Cotangens witzlos, da er keine neuen Informationen enthält, sondern mit  nur der Kehrwert des Tangens, also von
nur der Kehrwert des Tangens, also von  , ist. Und dementsprechend fehlt auch auf allen Taschenrechner eine Cotangens-Taste.
, ist. Und dementsprechend fehlt auch auf allen Taschenrechner eine Cotangens-Taste.
Nun lässt sich aber auch schnell zeigen, dass
tan (α) =  =
=

Das aber heißt, dass man den Tangens auch aus Sinus und Cosinus berechnen kann - und deshalb eigentlich auch die Tangens-Taste auf Taschenrechnern überflüssig ist: ![]()
Wenn man nun noch die Graphen  von Sinus und Cosinus vergleicht, stellt man zudem fest, dass der Graph des Cosinus nur um π /2 gegenüber dem des Sinus "versetzt" ist
von Sinus und Cosinus vergleicht, stellt man zudem fest, dass der Graph des Cosinus nur um π /2 gegenüber dem des Sinus "versetzt" ist
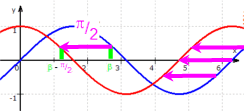
so dass man den Cosinus folgendermaßen aus dem Sinus erhalten kann:
cos (ß) = sin (α - π /2)
Also ist eigentlich sogar auch noch die Cosinus-Taste auf dem Taschenrechner überflüssig - und brauchen wir nur die Sinus-Taste: ![]()
(Grund dafür, die COS- und TAN-Taste dennoch auf dem Taschenrechner zu belassen, ist, dass man dann nicht andauernd Umrechnungen durchführen muss.)
Wo wir nun doch bei den Funktionsgraphen angekommen sind, noch kurz - wieder hübsch systematisch - dreierlei:
haben wir hier erstmals periodische Funktionen, die sich also nach links und rechts gleichmäßig und unendlich oft wiederholen
(bei der Sinus- und der Cosinus-Funktion mit unendlich vielen Nullstellen, Minima, Maxima und Wendepunkten in immer gleichem Abstand),
haben wir mit der Sinus- und dem Cosinus-Funktion beidseitig "beschränkte" Funktionen, weil beide niemals über +1 und unter -1 gehen
(der einzige Fall, in dem das früher der Fall war, waren jene simplen linearen Funktionen, die parallel zur x-Achse sind, also z.B. y = 3).
haben wir mit Tangens- und Cotangens Funktionen, die asymptotisch gegen Parallelen zur y-Achse laufen
(bislang waren "nur" bekannt:
asymptotisch gegen die x-Achse : die Exponentialfunktion,
asymptotisch gegen die y-Achse: die Logarithmusfunktion,
asymptotisch gegen die x- und die y-Achse: die Hyperbelfunktion ).