Die Welt ist ja für

viele SchülerInnen noch halbwegs in Ordnung, wenn - wie meistens üblich - die (Klassenarbeits-)Aufgaben direkt an den jeweils kurz vorher durchgenommenen "Stoff" anknüpfen.

Dann weiß man eben z.B.: wenn es um die Umwandlung eines Rechtecks in ein flächengleiches Quadrat (oder umgekehrt) geht,

1. schreit das nach dem Kathetensatz,
2. braucht man zusätzlich den Satz des Thales.

Um genau dieses "zusätzlich" geht es mir hier.

Dafür zwei markante Beispiele, und zwar je eins aus

1. der Algebra,
2. der sowie
3. der konstruktiven Geometrie

(ein langjähriger Mathelehrer kennt sämtliche [?] Fehlermöglichkeiten in- und auswendig - und kann die Fehler [worin durchaus eine gewisse Tragik besteht] dennoch kaum verhindern):

1. Bei den allseits ach so beliebten Termumformungen ist die Arbeitsanweisung "Vereinfache!" derart üblich, dass sie oftmals nicht mal mehr ausdrücklich formuliert wird, und "Vereinfache!" heißt dann oftmals u.a. "Beseitige die Klammern!"

Ein (scheinbar) sehr einfaches Beispiel ist

- (x+3)²

Da ist das Verfahren "1. Binomi" zwar nicht explizit benannt, solltete den SchülerInnen bei (x+3)² aber doch sofort einfallen:

(x+3)² = x² + 2 • 3 • x + 3² = x² + 6x + 9

Bezogen allein auf (x+3)² ist damit die implizite Aufgabe "Beseitige die Klammern!" erfüllt, und mit dem Minus davor ergibt sich scheinbar

    - (x+3)²             =

=-  x² + 6x + 9

Dabei wurde allerdings übersehen, dass das ganze (x+3)²negativ gesetzt werden muss - und somit auch das ganze x² + 6x + 9:

    - (x+3)²             =

=-[ x² + 6x + 9 ]  =

= -   x² - 6x  -  9

Dabei sei hier mal dahingestellt, ob der End-Term-   x² - 6x  -  9 denn tatsächlich einfacher als der Anfangs-Term - (x+3)² ist.

Bemerkenswert ist aber allemal, dass zur korrekten Lösung etwas wahrhaft Schizophrenes zu tun ist, nämlich

• zur Beseitigung der runden Klammern (  )
• dennoch zwischenzeitlich die eckigen Klammern [    ] eingefügt werden müssen

(vgl.   ).

Genau davon ist aber in der impliziten Aufgabenstellung "Beseitige die Klammern!" gerade nicht die Rede, sondern diese Aufgabenstellung fordert sogar das glatte Gegenteil - führt also scheinbar/bewusst in die Irre?

Wie aber kann man dafür sorgen, dass die SchülerInnen diesen Fehler zumindest ein wenig seltener machen?

Die einfachste (und ja nicht ganz falsche) Antwort ist da natürlich "pauken, pauken, pauken", also "500 Übungsaufgaben, und dann wird selbst der Dümmste es automatisch anwenden".

Mir scheint aber zusätzlich, dass die SchülerInnen Klammern

• als Schachteln

(vgl. )

• und regelrecht monolithisch erfahren müssen:

2. "»Gegeben ist« eine quadratische Pyramide mit der Grundseitenlänge 15 cm und der Höhe 12 cm. Wie lang sind die Seitenkanten?"

Ich gebe hier bewusst noch keine Zeichnung, da damit ja auch schon die Hälfte "verraten" würde (s.u.).

Ohne mitgelieferte Zeichnung ist die Aufgabe aber scheinbar missverständlich und sogar unlösbar, da ja auch eine zwar quadratische, aber schiefe Pyramide möglich ist, bei der die Kanten verschieden lang und zudem mit den Vorgaben der Aufgabe gar nicht zu errechnen sind:

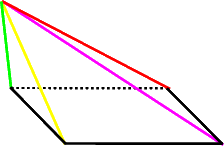
Fragt sich nur, ob das überhaupt ein reales Problem ist, werden doch die meisten SchülerInnen vermutlich automatisch an eine symmetrische Pyramide denken:

Aber es soll sogar der Fall willkommen sein, dass die einen oder anderen SchülerInnen an schiefe Pyramiden denken:

1. : welche Informationen braucht man zusätzlich, um dennoch (wie?) die verschiedenen Kanten berechnen zu können?
2. : alle (also auch die schiefen) quadratischen Pyramiden haben interessanterweise dasselbe Volumen.

(... beides Probleme, die aber wohl kaum erst in einer Klassenarbeit auftreten dürfen.)

Angenommen aber dennoch, die SchülerInnen denken alle sofort an symmetrische Pyramiden.

Ein erstes Problem, wenn keine Zeichnung mitgeliefert ist, besteht darin, sich das "Grundproblem" überhaupt vorstellen zu können:

1. haben viele SchülerInnen sowieso große Schwierigkeiten, sich dreidimensionale Dinge vorzustellen,
2. sind zweidimensionale Projektionen (im Buch, an der Tafel, im Heft) für sie oftmals auch keine Hilfen, da diese Projektionen verzerrt sind, also beispielsweise zur Lösung der vorliegenden Aufgabe so wichtige rechte Winkel nicht-rechtwinklig erscheinen,
3. muss man sich im dreidimensionalen Fall die Höhe der Pyramide mitten in diese hinein denken (!)

(und im zweidimensionalen Fall muss man ihren Fußpunkt korrekt in der Mitte der Grundfläche verorten),

4. gibt es in der Aufgabenstellung keinen Hinweis,

   1. , dass der Satz des Pythagoras (mehrfach) angewandt werden muss,

   2. , dass dazu zwei Hilfslinien - - - und ---nötig sind, die nun doch mal anhand einer zweidimensionalen Projektion gezeigt seien:

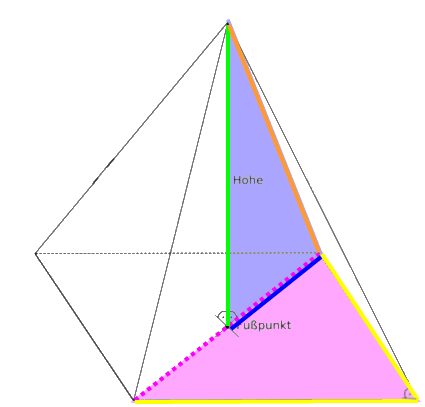
Wie schon gesagt: in dieser Zeichnung sieht keiner der vorkommenden und so dringend benötigten rechten Winkel auch tatsächlich rechtwinklig aus.

Und wenn nun die nötige Rechnung vorgeführt wird, wird gleichzeitig auch deutlich, wie "um die Ecke" gedacht diese ist:

• die änge der Strecke  Strecke - - - lässt sich durch Anwendung des Satzes des Pythagoras auf das rechtwinklige (!) lila Dreieck berechnen;
• --- ist dann halb so lang,
• die in der Aufgabe nachgefragte Länge der Seitenkante --- lässt sich durch nochmalige Anwendung des Satzes des Pythagoras, jetzt allerding auf das rechtwinklige (!) hellblaue Dreieck, berechnen.

Wie - zum Teufel - sollen SchülerInnen darauf kommen?

Und wäre man denn (als LehrerIn) selbst draufgekommen - wenn man nicht einschlägige Vorerfahrungen hätte.

Und die Vorerfahrungen bestehen eben

• in der "Prägung" auf rechtwinklige Dreiecke (Anwendbarkeit der Satzgruppe des Pythagoras) und
• der Fähigkeit, sie auch in zweidimensionalen Verzerrungen und in dreidimensionalen Gegenständen zu erkennen.

Diese "Prägung" kann meiner Überzeugung nach aber besonders gut in dreidimensionalem Modellbau stattfinden

(vgl. ).

3. Eine Standardaufgabe zur Satzgruppe des Pythagoras ist die Verwandlung eines Rechtecks in ein flächengleiches Quadrat oder umgekehrt

(wobei allerdings keiner so genau weiß, wozu diese Flächenumwandlung überhaupt gut ist).

Wir wählen hier mal die "Hin-Richtung" Rechteck → Quadrat:

"gegeben sei" also das Rechteck

 ,

das in ein flächengleiches Quadrat verwandelt werden soll.

"flächengleich" heißt dabei natürlich

• nicht, dass die Fläche dieselbe Form haben soll, denn dann wäre aus dem Rechteck niemals ein Quadrat zu machen,
• sondern dass das Ausgangsrechteck und das Endquadrat dieselbe Flächengröße haben sollen.

Bemerkenswert an der Aufgabenstellung ist schon, dass im Gegensatz zur Pyramiden-Aufgabe oben die konkreten Maße des Ausgangsrechtecks völlig uninteressant sind: es soll nur konstruiert, aber nicht gerechnet werden.

Bei der hier vorliegenden Umwandlungs-Aufgabe kommt man nun aber überhaupt nicht weiter, wenn man nicht umgehend denkt

(und zwar, obwohl es an keiner Stelle der Aufgabe erwähnt ist!):

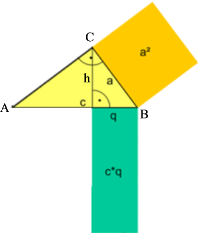
Und dann muss man erstmal eine geometrische Vorstellung vom Kathetensatz haben

(wobei uns hier der auf der rechten Seite genügen soll):

Hilfreich kann es zudem sein, wenn man noch den dynamischen

 
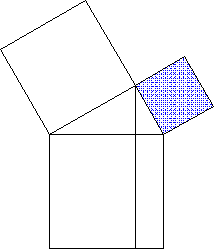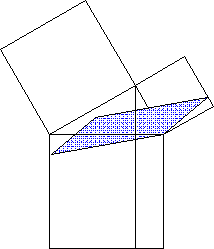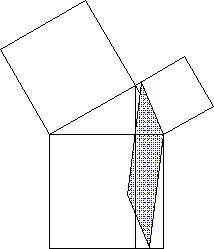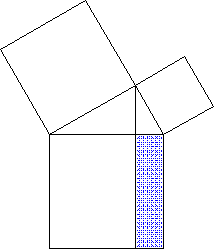
Beweis des Kathetensatzes

kennt, denn dann ergibt sich gleich die erste

(nicht in der Aufgabenstellung enthaltene!)

 Konstruktionslinie - - - :

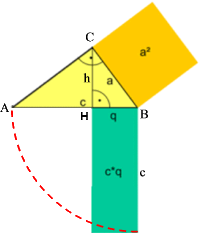
Überhaupt ist es wohl unabdingbar, dass man die üblichen Bezeichnungen der Dreiecksteile kennt und somit nach entsprechenden Punkten und Strecken suchen kann:

Daraus ergibt sich, dass A irgendwo auf der Linie --- und C irgendwo auf der Höhengerade --- liegen muss:

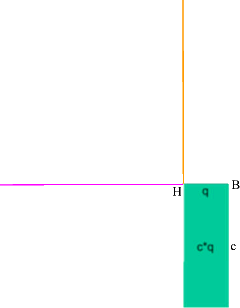
Die Lage von A lässt sich nun schnell mit der bereits genannten Hilfslinie - - - ermitteln: 

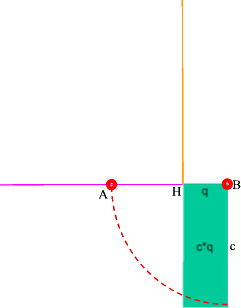
Völlig unklar ist aber auf Anhieb, wo auf der Höhengerade --- nun C liegt. 

Es sei allerdings an den zentralen Punkt der gesamten Konstruktion und überhaupt der Anwendbarkeit des Kathetensatzes erinnert: über der Hypothenuse AB ist ein rechtwinkliges Dreieck zu errichten. Nur leider passen da eine ganze Menge (unendlich viele) rechtwinklige Dreiecke drüber.

Am besten probiert man "einfach" einige aus, indem man mit dem Geodreieck so hantiert, dass seine Schenkel immer durch die Punkte A und B gehen:

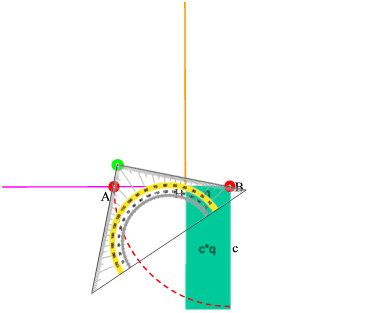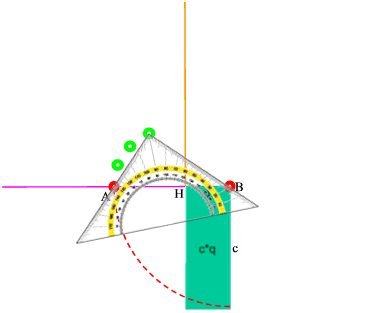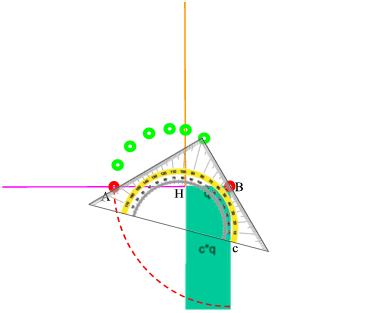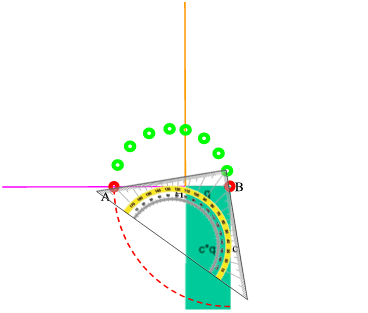
Vielleicht fällt einem dabei ja auf, dass all die grünen Punkte auf einem Halbkreis um den Mittelpunkt M der Strecke AB liegen:

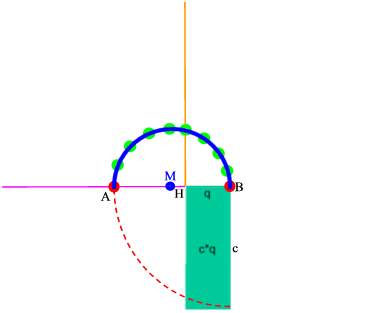
Damit aber haben wir den Thaleskreis wiederentdeckt, von dem in der Aufgabe ja auch nirgends die Rede war

(nebenbei: ein schöner Anlass, den Kathetensatz mit dem Thaleskreis in Verbindung zu setzen, ist unter   sichtbar).

Wenn man also um den Mittelpunkt M der Strecke AB einen Halbkreis schlägt, wird umgehend die Lage des Punktes C klar:

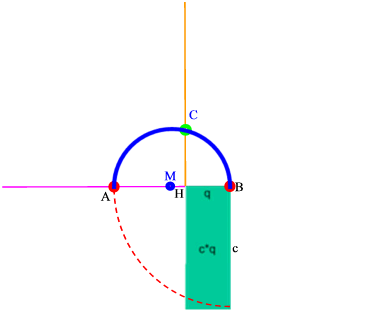
Und jetzt muss man nur noch die Strecken a und b einzeichnen

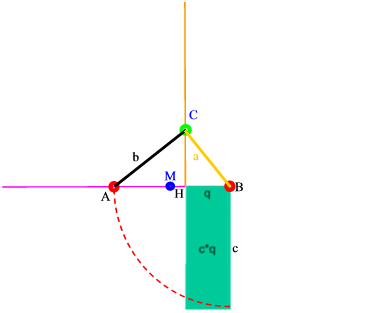
und über a das Quadrat konstruieren:

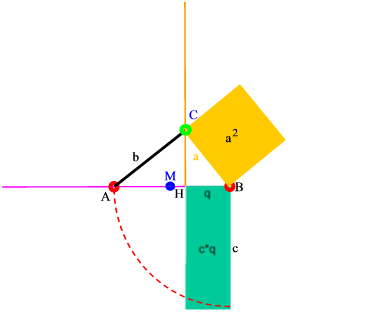
Ich hoffe, es ist deutlich geworden, dass erhebliche Überlegungen nötig sind, um die scheinbar ach so einfache Aufgabe zu lösen - wenn man nicht gleich das Patentrezept mitgeliefert bekommt.

Dennoch sollte man sich dauerhaft merken:

• Flächenumwandlung

1. Kathetensatz,
2. Satz des Thales !!!