Lösungsweg:
A.
Vorüberlegungen
1.
Liegt eine Binomialverteilung vor?
- wenn
ja
, vereinfachen
sich viele Rechnungen ungeheuer (s.u.),
-
wenn nein, sind die Rechnungen
enorm aufwendig.
Im vorliegenden Fall liegt
glücklicherweise tatsächlich
eine Binomialverteilung vor, da es nur
zwei Alternativen gibt:
- entweder
schauen mehr als 10
%
die Fernsehserie
-
oder es
schauen 10%
oder weniger die Serie.
2. Problemklärung
Es
lohnt sich immer, Extremfälle durchzudenken, weil man an ihnen
besonders deutlich
grundsätzliche
Probleme erkennen kann:
-
Im ersten
Extremfall haben wir bei der Befragung zufällig und unbemerkt
ausschließlich Fans der Serie am Telefon gehabt,
und dann kaufen wir aufgrund der scheinbar enormen Zustimmung neue Sendungen,
obwohl in Wirklichkeit die Zuschauerzahl nur gleich geblieben
oder sogar gesunken ist.
-
Im zweiten Extremfall haben wir bei der
Befragung zufällig ausschließlich
Serienmuffel am Telefon gehabt, und dann
kaufen wir aufgrund der scheinbar enormen
Ablehnung
keine neuen Sendungen, obwohl in
Wirklichkeit die Zuschauerzahl sogar gestiegen ist.
Sicherheit (also die Wirklichkeit
aller
Zuschauer) werden wir nie haben
(vgl. "Man ist sich auch der Zufälligkeit von
Stichprobenergebnissen bewusst"),
aber
immerhin doch mathematische, also halbwegs objektive
Kriterien für unsere Entscheidung.
3. Herausdestillieren
der Mathematik aus der Textaufgabe
10%
entspricht 0,1 , Stichprobenumfang n = 200
, 95%
entspricht 0,95
Man
möchte überprüfen, ob die
Beliebtheit der Sendung tatsächlich zugenommen
hat, ob also die Vermutung p >
0,1
zutrifft.
Bei der Aufstellung der
Hypothesen geht man so vor:
· Alternativhypothese
H1 = das, was
gezeigt werden soll,
im vorliegenden Fall also H1: p > 0,1
,
· Nullhypothese
H0 = das Gegenteil
dessen, was gezeigt werden soll,
im vorliegenden Fall also H0:
p
≤ 0,1
.
Vorerst ohne Erklärung: wir testen
-
nie unsere ursprüngliche
Hypothese H1
(merkwürdigerweise „Alternativhypothese“ genannt),
- sondern immer deren
Gegenteil,
also die Nullhypothese
H0
.
|
(Eselsbrücke: die
erste Hypothese, die wir aufstellen,
nennen wir passend H1,
und von da aus gehen wir noch einen Schritt zurück
zu H0.)
|
Bei
Ablehnung der Nullhypothese H0
wird unsere Alternativhypothese H1 angenommen.
(Das ist erstmal so um die Ecke gedacht, wie wenn man beweist, dass ein Elefant außerhalb
eines Kühlschranks ist, indem man zeigt, dass er nicht
in diesem ist.)
Im vorliegenden Fall also:
-
falls es nicht
so aussieht, dass 10% oder weniger die
Sendung gucken (H0),
-
nehmen
wir an,
dass
mehr als 10%
sie
gucken
(H1)
(und dann kaufen wir die
nächste Staffel).
H0 soll
im Folgenden durch die Telefonumfrage getestet werden.
Die
geforderte Sicherheit von 95%
bzgl. der Nullhypothese H0 bedeutet,
dass wir
- uns
mit einer Wahrscheinlichkeit von 95%
richtig entscheiden, wenn wir die
Nullhypothese H0:
p
≤
0,1
annehmen – und somit unsere
Alternativhypothese H1:
p > 0,1
ablehnen
(also keine
zusätzlichen Sendungen kaufen),
- also
mit einer Wahrscheinlichkeit von
100% - 95%
= 5% falsch entscheiden, wenn wir die Nullhypothese H0:
p
≤
0,1
ablehnen – und dann natürlich
unsere Alternativhypothese H1:
p > 0,1
annehmen
(und zu Unrecht neue Sendungen kaufen).
Man spricht dann auch vom
„Signifikanzniveau a ≥ 5%“.
Insgesamt
liegen wir also mit einer
Wahrscheinlichkeit von nur 5% falsch, wenn wir
unsere Alternativhypothese H1:
p > 0,1
annehmen.
(und neue Sendungen kaufen, was dann allerdings viel rausgeschmissenes Geld
bedeuten würde).
Nun
müssen wir noch die Entscheidungsbereiche bzgl.
H0
definieren:
(H1
also
ablehnen),
- den
Ablehnungsbereich
von H0,
in dem die Anzahl der Umfrageantworten „ich schaue die Serie“ liegt,
bei der wir H0
ablehnen
Die bisherigen
Überlegungen müssen allesamt stattfinden, bevor
die Umfrage durchgeführt wird. Es muss also immer schon vorher
feststehen, wie man mit späteren Umfrageergebnissen
umgehen wird, egal, wie die Umfrage dann ausfällt. Sonst könnte man ja hinterher
eine Rechnung erfinden, mit der unliebsame Umfrageergebnisse nachträglich
schöngerechnet werden.
B. Mathematisierung
Dieser
Teil handelt ausschließlich
von der Nullhypothese
H0:
p ≤
0,1 . Auf unsere ursprüngliche Alternativhypothese H1:
p >
0,1
werden wir erst im Teil D. zurückkommen.
Aus
der Aufgabenstellung und den Vorgedanken oben entnehmen wir folgende Werte:
-
Nullhypothese
H0:
p ≤
0,1
,
- Signifikanzniveau
a ≥ 5% ,
-
p
= 0,1
(ab
hier rechnen wir also nicht mehr mit einem schwammigen p
≤ 0,1
, sondern mit einem exakten Wert, nämlich p
= 0,1
;
zu
diesem alles entscheidenden Übergang von p
≤ 0,1
zu p = 0,1
siehe die Schlussbemerkung
ganz am Ende dieses Textes)
- Stichprobenumfang n =
200
.
Als
einzige Formeln, die wir bei Binomialverteilungen
brauchen, haben wir:
-
Erwartungswert
μ =
n
•
p
,
-
Varianz
σ2
=
μ
•
(1 – p) =
=
n
• p • (1 – p) ,
-
Standardabweichung
σ
=
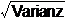 =
=
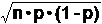 .
.
Damit sind wir vollständig in der Mathematik
– und können für einige Zeit die Aufgabe bzw. den Anwendungsanlass
vergessen.
Insbesondere ist an der Aufgabe
alles bloße Verzierung (und absichtliches Versteckspiel?), was im
Folgenden frech durchgestrichen ist:
| „Eine
Fernsehserie hatte im letzten Jahr eine mittlere Einschaltquote von 10%. Das Management des Senders
vermutet, dass die Beliebtheit der Serie im letzten Quartal des
Vorjahres sogar etwas zugenommen
hat. Weitere Serien sollen dazugekauft werden, wenn die
Beliebtheit der Sendung tatsächlich zugenommen hat.
Dazu sollen 200
Personen mittels einer Telefonaktion befragt werden. Man ist
sich auch der Zufälligkeit von Stichprobenergebnissen bewusst und gibt
sich mit einer Sicherheit von mindestens
95%
des Befragungsergebnisses zufrieden.“
|
Wirklich mathematisch
an der Aufgabenstellung ist also nur
„…
10%. … zugenommen
… zugenommen …
200 … Sicherheit von mindestens 95% ….“
Daran
wird aber deutlich, wodurch die typischen Schwierigkeiten mit
Textaufgaben zustande kommen:
man sieht
- anfangs vor lauter Bäumen
(ablenkenden Anwendungsdetails) den Wald (die
Mathematik) nicht mehr
- und am Ende vor lauter
Rechnen nicht mehr, was das mathematische
Ergebnis im Hinblick auf die Anwendung bedeutet;
- die
Mathematik
- tritt manchmal ausdrücklich
auf und ist dann leicht erkennbar
(in der vorliegenden Aufgabe bei
10%, 200 und 95%
),
- ist
manchmal hinter umgangssprachlichen
Formulierungen verborgen
(in
der vorliegenden Aufgabe bedeutet „zugenommen“
das
mathematische Zeichen >
[größer] und „mindestens“ das
Zeichen ≥
[größer oder gleich]).
Alles im Folgenden Berechnete gilt
für sämtliche Binomialverteilungen, in denen
dieselben Werte
- Nullhypothese
H0:
p
≤ 0,1
,
-
Signifikanzniveau
a ≥ 5% ,
-
p
= 0,1
,
-
Stichprobenumfang n =
200
.
vorkommen
(also auch, wenn statt von Zuschauerzahlen
beispielsweise von kaputten Schrauben die Rede ist)
.
Mehr
noch: da das Prinzip der Rechnungen dasselbe
bleibt, wenn man andere Anfangswerte einsetzt
(z.B.
-
Nullhypothese
H0: p
≤ 0,6
,
-
Signifikanzniveau a ≥ 7% ,
- Stichprobenumfang n =
800
),
gelten die folgenden
Rechnungen im Prinzip für alle Binomialverteilungen
bzw. sind die Rechnungen leicht (?) auf Binomialverteilungen mit anderen
Anfangswerten übertragbar.
(Das ja eben ist der Grund
-
einerseits
für
die abgenagte Abstraktheit der Mathematik,
-
andererseits
für
ihren ungeheuren Erfolg, soweit sie sich auf
Anwendungen bezieht:
dass sie
- überschaubar viele
Rechenwege [„Algorithmen“]
- für potentiell unendlich viele
Anwendungsprobleme anbietet.
Z.B. ist
- ein einziger
mathematischer Satz, nämlich der Satz des Pythagoras,
- ein
Rechenverfahren für alle, also unendlich
viele rechtwinklige[n] Dreiecke.)
C.
 rein
innermathematischer Teil
rein
innermathematischer Teil
Wenn man erstmal derart in die
reine Mathematik entfleucht ist, braucht man eigentlich nur noch die
mathematische Symbolsprache. Leserfreundliche
Autoren fügen aber - je nach Vorkenntnissen ihrer Zielgruppe -
doch noch einige knappe „Regieanweisungen“ bzw. überleitende
Erklärungen hinzu. Insgesamt sieht das dann z.B. so aus:

Alle Klarheiten beseitigt?
Gehen
wir die zitierte Passage also ein bisschen langsamer,
d.h. mit längeren bzw. mehr Zwischenerklärungen an:
- als
wichtigsten Kennwert jeder Wahrscheinlichkeitsverteilung berechnen wir
zu allererst den Erwartungswert
μ :
| |
m
=
n • p
=
= 200
• 0,1
= 20
oder kurz
m =
20 ;
|
- mit
diesem Erwartungswert
können wir nun auch leicht die Varianz und
daraus folgend die Standardabweichung
berechnen:
| |
o Varianz σ2 =
m
• (1 – p ) =
= 20
• (1 –
p ) =
= 20 • (1
–
0,1)
=
= 20 •
0,9 =
18
oder kurz
Varianz σ2
=
18
(Es
sei kurz daran erinnert, dass die
Varianz
keine aussagekräftige
Bedeutung hat, sondern nur ein notwendiger rechnerischer Zwischenschritt
auf dem Weg hin zur Berechnung der bedeutsamen
Standardabweichung ist:)
o Standardabweichung
σ
=
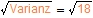 ≈
4,26 ≈
4,26
oder kurz
Standardabweichung σ
= 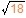 ≈ 4,26 ≈ 4,26
|
Wiederum ohne Begründung: um eine
95%ige
Sicherheit zu erreichen, legen wir um den
Erwartungswert
m
=
20
den
Annahmebereich mit dem
Radius
|
r
= 2 •
σ =
= 2 •
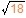 = =
≈
2 •
4,26 =
= 8,52
oder
kurz
r ≈
8,52
bzw.
aufgerundet
r
=
9
.
|
(Vgl.
 ;
;
Es
ist zudem anzumerken, dass wir mit der
2σ-Regel
eine einfachere Regel verwenden als der
Aufgaben-Autor mit seiner 1,64σ-Regel
und dass wir daher auch zu anderen Ergebnissen
kommen werden als er.)
Mit
r =
9 ergibt sich
- als
linke
Grenze
L
des
Annahmebereichs
L =
m
–
r
=
= 20
–
9
=
=
11
oder kurz
L = 11
,
- als
r
echte Grenze
R
des
Annahmebereichs
R =
m
+
r
=
= 20
+
9
=
=
29
oder
kurz
R =
29
.
|
(Durch das Aufrunden von
r auf 9 sind zum
Annahmebereich
zusätzlich die beiden
Randzahlen 11 und
29 hinzugekommen.)
Schauen wir uns nun
die
200er-Stichprobe und daran
vergrößert den besonders wichtigen
Annahmebereich an:
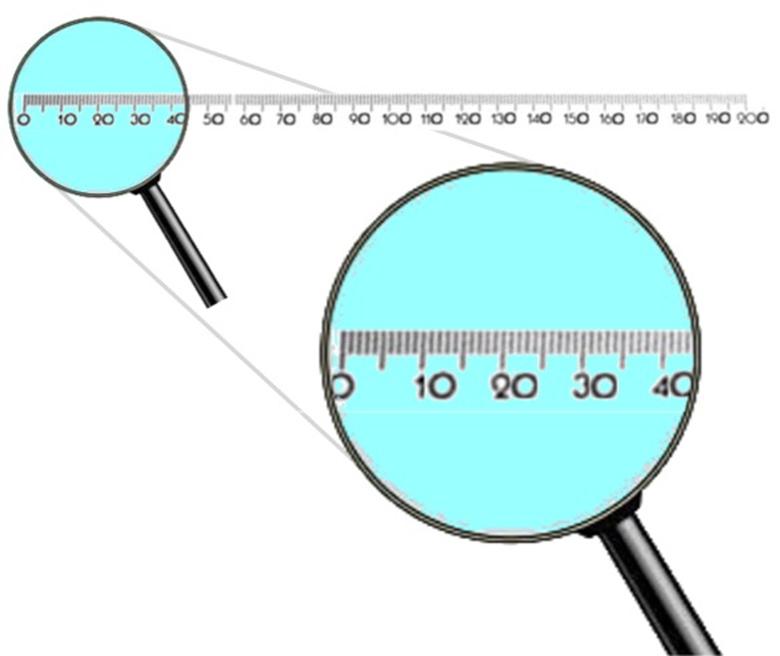
Wenn wir nun in den
vergrößerten Bereich die oben berechneten Werte eintragen,
ergibt sich
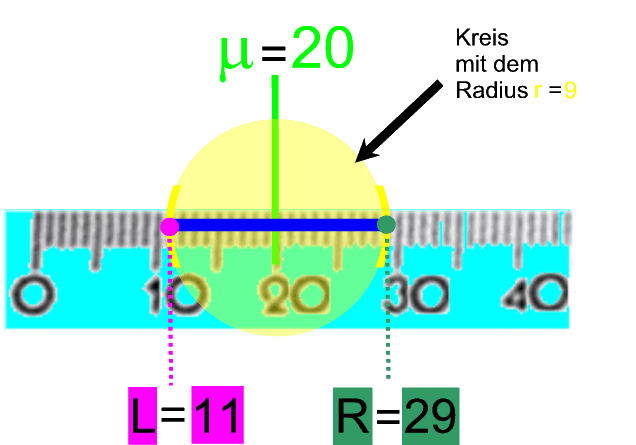
und somit (vorerst) als
Annahmebereich
der Nullhypothese das Intervall [
11 ;
29 ] .
Machen
wir uns nach all den Rechnungen nun aber klar, was das im Hinlick auf
die Nullhypothese bedeuten
würde:
-
wir würden die Nullhypothese
annehmen
(also von einer
schlechten
Akzeptanz der Fernsehserie ausgehen und daher keine
neue Staffel kaufen),
wenn
zwischen
11 und
29 der insgesamt
200 befragten Zuschauer die Serie anschauen;
(also
unsere ursprüngliche Alternativhypothese annehmen und somit eine
neue Staffel kaufen
würden),
wenn
-
entweder weniger
als 11
Befragte, also zwischen 0 und 10
Befragte (Bereich
BL
)
-
oder mehr
als
29
Befragte, also zwischen 30 und
200
Befragte (Bereich BR
)
die Serie anschauen:
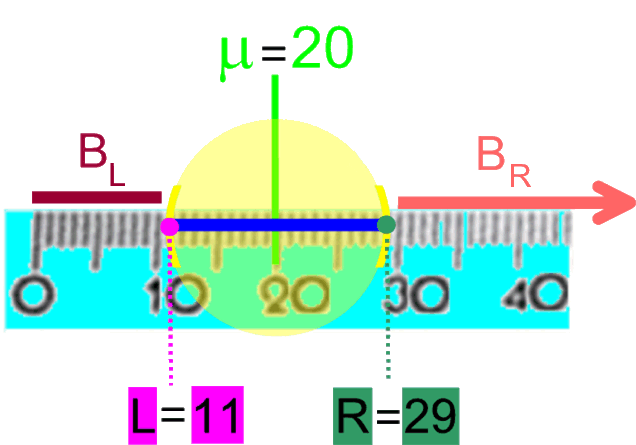
Nun würde der Fall a. aber
bedeutet, dass wir
-
von
einem
erhöhten Serienkonsum ausgehen und eine neue Staffel
kaufen würden,
-
wenn besonders
wenige
(nämlich zwischen 0 und 10) Befragte die Serie gucken würden.
Dazu müssten wir
z.B. denken:
"Wenn besonders wenige
Leute die Serie angucken, kaufen wir die neue Staffel aus purem Trotz erst recht. Uns schert
also nicht im mindesten die geringe Nachfrage der
Zuschauer, bzw. wir werden durch ein vermehrtes Angebot
eine höhere Nachfrage überhaupt erst
erzeugen.“
Mag sein,
dass einige Fernsehsender tatsächlich so denken, aber wieso machen sie
dann überhaupt eine Umfrage?!
Da
der
Bereich BL
somit ein unsinniger
Ablehnungsbereich ist,
schlagen wir ihn tolldreist
zum ursprünglich berechneten
Annahmebereich
der Nullhypothese
und erhalten als neuen
|
Annahmebereich
der Nullhypothese
das
Intervall
[ 0 ;
29 ] :
|
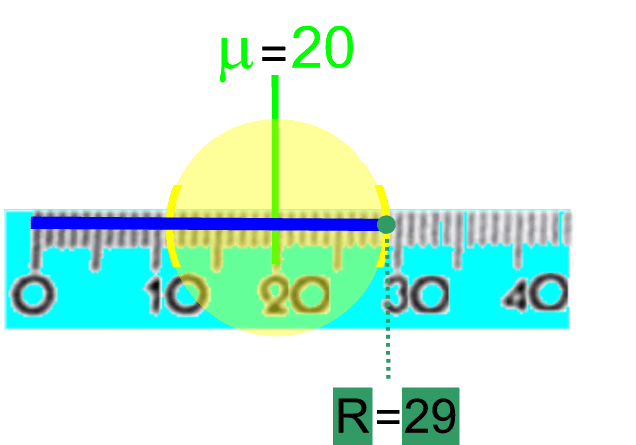
|
Für
den Ablehungsbereich
der
Nullhypothese bleibt dann nur noch der Bereich
BR, also das
Intervall
[30 ; 200] : |
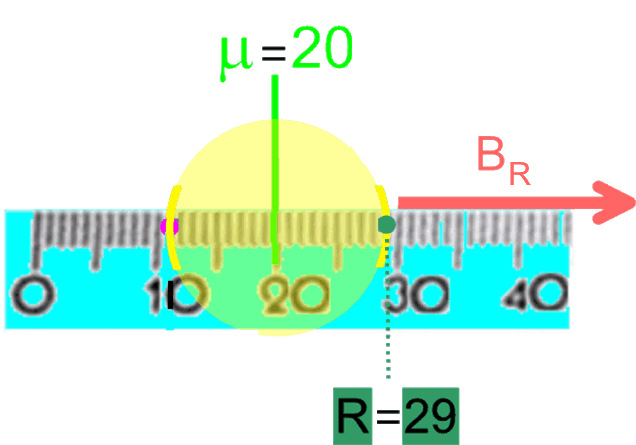
Da uns das mathematische Ergebnis
links also gar nicht interessiert, spricht
man auch von einem „
rechtsseitigen“ Hypothesentest
(in anderen Fällen gibt es
auch links- oder beidseitige
Hypothesentests).
In diesem Kapitel B. war mit einer
einzigen kleinen Ausnahme nur von der Nullhypothese die Rede. Da nun
aber alle wichtigen Werte bzgl. der Nullhypothese berechnet sind, können wir endlich zu
unserer ursprünglichen, also der
Alternativhypothese
zurückzukehren
(bzw. um das Elefantenbild von
oben nochmals zu bemühen: vom Nichtvorhandensein
des Elefanten innerhalb des Kühlschranks auf seine
Anwesenheit außerhalb des Kühlschranks zu schließen):
D.
 Rückkehr zur ursprünglichen
Alternativhypothese
und zum "Fernsehproblem"
Rückkehr zur ursprünglichen
Alternativhypothese
und zum "Fernsehproblem"
|
Bei einer
Binomialverteilung, bei der es nur zwei komplementäre Möglichkeiten gibt
(hier
ist
-
der Annahmebereich
der
ursprünglichen Alternativhypothese
- eben gerade der
Ablehungsbereich
BR
der
Nullhypothese
(und umgekehrt) .
In
unserem Fall ist der Annahmebereich der ursprünglichen
Alternativhypothese
also
BR
, d.h. das
Intervall [30 ; 200]:
|
Wenn in dem Telefoninterview zwischen 30
und 200 Interviewte sagen, dass sie (regelmäßig) die Fernsehserie
gucken, halten wir unsere Alternativhyothese
für hinreichend
(mit einer Sicherheit von 95%) belegt - und kaufen wir
also die nächste Staffel. |
95%ige Sicherheit bedeutet dabei, dass
wir bei mehrfacher Wiederholungen dieses Entscheidungsverfahrens nur in
5% aller Fälle
(also
bei nur einer von zwanzig Entscheidungen)
falsch lägen
(hier wurde der Konjunktiv benutzt,
weil das Entscheidungsverfahren vielleicht nur ein Mal angewandt wird,
nämlich bei der vorliegenden Fernsehserie).
Dabei
ist es natürlich durchaus möglich (aber doch unwahrscheinlich), dass
wir bereits bei der ersten (und evtl. einzigen)
Entscheidung falsch liegen.
|
Im Nachhinein wird auch klar, wieso man nicht
direkt die
Alternativhypothese
angeht, sondern den Umweg
über die Nullhypothese einschlägt:
-
ein philosophisch-psychologischer
Grund:
in
der Aufgabenstellung heißt es:
"Das
Management des Senders vermutet, dass die Beliebtheit der Serie im
letzten Quartal des Vorjahres sogar etwas zugenommen hat."
Das
heißt aber doch, dass das Managment nicht
unvoreingenommen an die Sache rangeht,
sondern eine vorgefasste Meinung (Vermutung) hat.
(Allerdings
scheint das Managment
- einerseits
vom Erfolg der Serie überrascht
zu sein ["sogar"],
- anderseits
demütig nur eine kleine
Verbesserung für möglich zu halten ["etwas"].)
Solch
ein Vorurteil ist aber immer gefährlich, da es schnell betriebsblind
gegenüber jenen Aspekten macht, die der vorgefassten Meinung
widersprechen. Deshalb sollte nach dem Philosophen
Karl Popper (nicht nur) jeder Wissenschaftler sogar gezielt nach jenen
Aspekten suchen, die seiner vorgefassten Meinung
widersprechen. In unserem Fall ist aber eben die
Nullhypothese das Gegenteil der
ursprünglichen (Alternativ-)Hypothese.
-
mathematische
Gründe:
-
erster
mathematischer Grund:
- wenn
wir bei der Bestimmung
des Annahmebereichs
der Nullhypothese den Radius r
dieses Annahmebereichs durch Aufrunden zu groß
gewählt haben,
-
wird
damit der Ablehnungsbereich
der Nullhypothese
zu klein,
-
und
somit wird auch der Annahmebereich
der
ursprünglichen
Alternativhypothese zu klein.
Letzteres
bedeutet aber, dass wir unsere ursprüngliche
Alternativhypothese nur
unter sehr strengen
Bedingungen akzeptieren, unserer vorgefassten Meinung gegenüber also
sehr kritisch
sind.
- ein
zweiter mathematischer oder fast schon
wieder philosophischer Grund wird erst
unten in der Schlussbemerkung
sichtbar.
Wieder ohne Nachweis: im Regelfall kommt
(sogar dann, wenn
man nicht rundet)
nicht derselbe Annahmebereich
der
Alternativhypothese
heraus, wenn man diesen direkt
bestimmt, also ohne
Umweg über die Nullhypothese.
Schlussbemerkung
... zum tieferen Verständnis unseres obigen Vorgehens
wie überhaupt der gesamten Wahrscheinlichkeitsrechnung:
wir waren oben von p
≤
0,1
zu p = 0,1
über- oder genauer zurückgegangen.
Auf den ersten Blick diente das allein der Arbeitserleichterung, da
mit Gleichungen
viel einfacher gerechnet werden kann als mit
Ungleichungen.
In Wirklichkeit ist diese Arbeitserleichterung aber "nur" ein (höchst
willkommenes) Abfallprodukt viel
fundamentalerer
Überlegungen
(und damit ist die
Arbeitserleichterung nicht bloße, evtl. sogar mathematisch falsche oder zumindest
doch ungenaue Willkür)
:
"fundamental", weil hier überhaupt erst
klar wird,
Die weise
Selbstbeschränkung besteht darin, ausschließlich mit der
einzig
bekannten Tatsache
zu argumentieren, von der man aus der Vergangenheit
(und nur diese ist
sicher!)
weiß: dass bislang
genau 10% der
Zuschauer
die Fernsehserie geguckt haben.
Nun verlängert man
diese exakt 10% in die Gegenwart
und Zukunft ,
d.h. man geht davon aus, dass
sich
nichts ändert,
-
also auch in der Gegenwart und Zukunft
10% der Zuschauer die Fernsehserie gucken
(werden) und
somit
-
p
gleich 0,1
ist bzw. sein wird .
Nun können wir aber
niemals das Fernsehverhalten aller
Zuschauer in der Zukunft
herausbekommen,
sondern nur eineTelefonumfrage mit n = 200 Personen machen.
Bei dieser zukünftigen
Telefonumfrage spielt nun aber der unplanbare Zufall, können nämlich
z.B. auch die oben genannten, höchst irreführenden Extremfälle eintreten.
Deshalb gehen wir der Einfachheit halber davon aus, dass
die Befragten in der zukünftigen Telefonumfrage weiterhin mit der aus der Vergangenheit bekannten
Wahrscheinlichkeit von p gleich
0,1
Zuschauer unserer Sendung sind. Und diese Annahme (dass
sich nichts
ändern wird) ist eben die Nullhypothese!
Nun messen wir in einem Gedankenexperiment wir den Ausgang der zukünftigen
Telefonumfrage an einem fiktiven
Zufallsexperiment, bei dem völlig
zufällige Antworten erfolgen, allerdings mit der altbekannten
Wahrscheinlichkeit p gleich
0,1.
Zwar vermuten und hoffen wir mit den Managern des
Fernsehsenders, dass
Für Vermutungen mag es ja immerhin noch
Indizien geben
(die im Aufgabentext allerdings nicht genannt werden),
während Hoffnungen zwar immer
ehrenwert, aber sicherlich
keine - wie man neudeutsch sagt -
"belastbaren" Fakten sind.
Eben deshalb
klammern wir uns an das einzige, aus der Vergangenheit bekannte Faktum,
nämlich p = 0,1 , was sozusagen die halbe Nullhypothese
ist.
|
|
(Drei kurze
Ergänzungen: -
kann
der Mensch im Grunde ja sowieso nur mit seinen Erfahrungen aus der
Vergangenheit auf die Zukunft schließen,
-
könnte man die Unterstellung, dass sich
nichts ändert, auch als "konservativ"
bezeichnen, -
ist
das soeben Gesagte der zweite, oben nur angedeutete mathematische Grund dafür, nicht mit der
ursprünglichen Alternativ-, sondern mit der
Nullhypothese anzufangen.)
| |
In der Gegenwart können wir nur rechnen, und zwar anhand
eines Gedankenexperiments, das folgendermaßen aussieht:
|
|
(also sozusagen die
halbe
Nullhypothese),
|
(Man kann sich das
auch so vorstellen, dass wir Kugeln aus einer Urne ziehen, wobei 10 %
der Kugeln grau sind und 90 % z.B. orange.
Unsere Frage ist
nun, wieviele der
gezogenen Kugeln bei 200fachem
rein zufälligem Ziehen [mit Zurücklegen] vermutlich
grau sein werden.
Genau dies ist aber die Rechnung, die wir oben lang und
breit durchgeführt haben
[und hier endlich
sei drauf hingewiesen, dass wir oben
Als entscheidende
Erkenntnis
haben wir dort herausgefunden:
die Anzahl der grauen Kugeln wird mit
95%-iger Sicherheit im Annahmebereich der
Nullhypothese liegen, d.h. im Intervall
[
0 ;
29
]
:
 )
)
Und nun nehmen wir uns vor, die zukünftige
Telefonbefragung nach
ihrem Abschluss an diesem rein
zufälligen Gegenwarts-Gedankenexperiment
zu messen:
Möglichkeit: in der
Telefonbefragung tritt nur das ein,
(mit 95%-iger
Sicherheit)
bei rein zufälligem Vorgehen zu erwarten war
(allerdings unter der Voraussetzung, dass p unverändert
gleich 0,1 ist),
| | Für
dieses erste Ergebnis gibt es zwei Interpretationsmöglichkeiten
| (man höre und staune: in der Wahrscheinlichkeitsrechnung sind genauso [letztlich
außermathematische und immer unsichere] Interpretationen
unvermeidbar bzw. nötig wie bei der Behandlung von Literatur im Deutschunterricht):
|
| | -
die Hypothese, dass auch in der Zukunft p gleich 0,1
sein wird,
wurde
bestätigt, weil tatsächlich auch dann p noch gleich 0,1 oder sogar kleiner war;
-
die Hypothese, dass auch in der Zukunft
p gleich 0,1
ist, wurde nur
scheinbar
bestätigt, weil
Nun haben wir aber keine Chance herauszufinden, was
alle Zuschauer tatsächlich bzw. in Wirklichkeit gucken, woraus wir sozusagen mangels
Masse folgern, dass
-
a.
(und nicht b.) zutrifft, also -
die
Nullhypothese
nach wie vor richtig ist, weil
-
auch zur Zeit der Telefonumfrage noch
immer genau 10
% (oder sogar weniger) die Serie gucken,
weshalb wir keine neue Staffel kaufen.
| |
-
Möglichkeit: in der Telefonbefragung
ergeben sich mehr Seriengucker, als bei rein zufälligem Vorgehen zu erwarten war, nämlich
| |
Auch für dieses zweite Ergebnis gibt es
zwei Interpretationsmöglichkeiten:
| |
-
die
Hypothese, dass auch in der Zukunft
p gleich 0,1
sein wird, wurde widerlegt,
weil p tatsächlich größer
als 0,1 geworden
ist; -
die
Hypothese, dass auch in der Zukunft
p gleich 0,1
ist, wurde nur
scheinbar
widerlegt, weil
Nun haben wir aber auch hier wieder keine Chance herauszufinden, was
alle Zuschauer tatsächlich bzw. in Wirklichkeit gucken, woraus wir sozusagen mangels
Entscheidungsalternativen folgern, dass
-
a.
(und nicht b.) zutrifft, also -
die
Nullhypothese
inzwischen falsch
ist, weil -
zur Zeit der Telefonumfrage mehr als 10 % die Serie gucken,
weshalb
wir neue Staffel kaufen.
| |
Bei beiden möglichen Ergebnissen der
Telefonumfrage glauben (!) wir diese also. Wir
(wobei
immer die Gefahr besteht,
[so entstehen
dann pauschalisierende Vorurteile wie z.B.: zwei
Juden sind geldgierig ⇒ alle Juden sind
geldgierig],
- also zu vergessen, dass alles
nur ein Modell ist),
- und
ziehen mangels besserer Möglichkeiten allein aufgrund unserer Kenntnis des Ausfalls
der Telefonumfrage unsere Konsequenzen
(neue
Staffel kaufen oder nicht kaufen).
Dabei
(das Umfrageergebnis spiegelt
dann korrekt
die Gesamtwirklichkeit),
(das
Umfrageergebnis spiegelt dann nur
scheinbar [ohne dass wir das merken]
die Gesamtwirklichkeit).
Siehe dazu
 .
.
Hier nun aber muss zum zweiten Mal eine letztlich
nichtmathematische Interpretation
erfolgen:
wenn Privatsender in 5
% aller Fälle wegen einer falschen Entscheidung pleite gehen,
ist das ja nur nur erfreulich,
-
wenn aber
ein Medikament
in
5 % aller
Fälle tödlich
ist, ist dieses
Medikament wohl unverantwortbar
(und
hätten wir besser
von Anfang an eine 3σ-Umgebung
für 99,7%-ige Sicherheit gewählt!).
Das alles
Entscheidende an unserem Vorgehen besteht darin, dass wir
-
die
konkreten
Ergebnisse der Telefonumfrage
-
an einem
lange
vor der
Telefonumfrage durchgerechneten, rein
zufälligen Gedankenexperiment
messen
-
und
dabei erstmal davon ausgehen, dass sich p
nicht
ändert (halbe Nullhypothese).
Kürzer: dass wir
uns anschauen,
Ultrakurz: indem wir
alle konkreten Ergebnisse mit dem reinen
Zufall vergleichen.
(in der Medizin
beispielsweise durch Placebo-, also völlig unwirksame Tabletten).
Dabei ist zu beachten:
-
zwar messen wir das Telefonumfrageeregebnis
am nackten Zufall,
aber das heißt
nicht, dass auch das
Umfrageeregebnis selbst vollständig zufällig ist
(vgl.:
Unser gesamtes Vorgehen wäre ja auch völlig witzlos,
wenn auch das Umfrageergebnis völlig zufällig wäre. Vielmehr vertrauen (!) wir
doch darauf, dass es
(wenn auch mit einem gewissen "Restrisiko")
das reale, also nicht zufällige Zuschauerinteresse
spiegelt.
Wir müssen also genau festhalten:
-
es ist keineswegs ein Zufall, wie viele Zuschauer
(in der Gesamtbevölkerung) die Ferrnsehserie gucken; nur leider ist uns
dieses Faktum völlig unzugänglich: wir können nicht
alle (einige
millionen?) Zuschauer befragen;
-
hingegen spielt der Zufall eine gewisse doppelte
Rolle
(üblicherweise rufen seröse Unfrageinstitute nicht
irgendwelche Leute an
[z.B. die ersten 200 im berliner
Telefonbuch],
sondern haben da vorweg gewisse Auswahlregeln
[z.B. einen Querschnitt durch die Generationen]).
-
der Frage, ob die zum Interview Ausgewählten
überhaupt repräsentativ antworten.
Es sind sogar Fälle denkbar, bei denen überhaupt kein
Zufall vorliegt, z.B.
(früher nannte man sowas
 );
);
(und seien sie noch so zufällig ausgewählt)
die Serie gucken
(und werden wir die neue Staffel kaufen).
Nur werden wir leider
nie erfahren, was für einen
Volltreffer wir mit der Telefonbefragung gelandet haben,
- dass nämlich die
Telefonbefragung nicht nur ziemlich genau,
also halbwegs repräsentativ ist, sondern sogar
exakt die Gesamtbevölkerungt
widerspiegelt,
- dass also tatsächlich
alle Menschen
nicht nur in der Telefonumfrage, sondern auch in der Gesamtbevölkerung die Serie gucken.
|
Vielmehr könnte es ja auch
sein, dass
-
wir durch einen riesigen Zufall im
Telefoninterview die einzigen 200 Menschen erwischt haben, die die Serie
gucken,
-
und dass der ganze Rest der Bevölkerung die Serie
nicht guckt
(vgl.: Prinz William wird nie
[zumindest nicht mit mathematischer
Sicherheit]
erfahren, dass
[nicht "ob"]
Kate Middleton tatsächlich ihn liebt und nicht bloß
sein Geld und seinen Status teilen will; da bleibt ihm nur etwas völlig
unmathematisches: Vertrauen).
die Zeitenfolge


In der Mathematik ist
-
die Vergangenheit
immer sicher, kann bei ihr also von
Wahrscheinlichkeit und damit auch
Wahrscheinlichkeitsrechnung keine Rede
mehr sein,
-
die Zukunft
immer offen und damit das
eigentliche Tummelfeld der
Wahrscheinlichkeitsrechnung,
-
die Gegenwart
jener Augenblick, in dem aus vielen
zukünftigen Möglichkeiten genau
ein (dann sicheres)
Faktum wird
("Wahrscheinlichkeitskollaps").
Da die Gegenwart
sich durch die Zeit bewegt, schauen
wir uns hier zwei Gegenwarten
an:
1. Gegenwart
, z.B. 25.10.2012

- wir wissen aus der
Vergangenheit
(z.B.
17.10.2012 ), dass
früher 10% der Zuschauer die Fernsehserie angeguckt haben
(wobei es höchst fraglich ist, ob dieses
vergangene Ereignis wirklich
sicher war, entstammte es vermutlich doch
auch schon einer mehr oder minder repräsentativen
Umfrage),
- ausgehend davon stellen wir in der
Gegenwart die (Alternativ-)Hypothese auf
und führen alle obigen Berechnungen durch, mit denen wir
-
später die Telefonumfrage bewerten wollen, die
noch in der Zukunft liegt
(z.B. 1.12.2012 ).
Nun vergeht die Zeit, und irgendwann sind wir in der
2. Gegenwart , z.B.15.12.2012
:
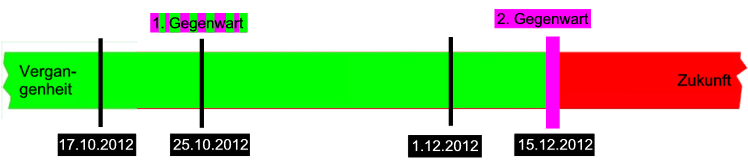
- inzwischen hat die Telefonumfrage (am
1.12.2012) stattgefunden
und ist sie ausgewertet worden
(z.B. "42 der 200 Befragten haben angegeben, dass sie
die Serie gucken"),
d.h. Umfrage und Auswertung liegen inzwischen auch
schon in der Vergangenheit und sind somit
unabänderlich-sicher;
- nun messen wir (in der neuen, zweiten Gegenwart) das
Umfrageergebnis an den Entscheidungskriterien, die wir in der
ersten
Gegenwart
(die inzwischen sozusagen
Vorvergangenheit geworden ist)
aufgestellt
hatten: das ist der eigentliche Hypothesentest
(weil 42 im Annahmebereich der
Alternativhypothese
liegt, würden wir entscheiden: "es gucken tatsächlich inzwischen
mehr als 10 % der Zuschauer die Serie, und deshalb kaufen wir die neue Staffel").

"Mrs. Black and White
She's never seen a shade of grey"
(Amy McDonald)
'[...] you're hot then you're cold
You're yes then
you're no
You're in then you're out
You're up then you're down
You're wrong when it's right
It's black and it's white [...]"
(Katy
Perry)
Unsere Aufgabe ist ein Musterbeispiel für
Binomialverteilungen, an denen aber auch wirklich
alles "bi" ist: sie
funktionieren ausschließlich nach der zweiwertigen,
gnostischen Logik von
("es gibt nur zwei Meinungen:
meine und die falsche"),
(Pablo
Picasso, was ja nur seine eigenen Komplexe zeigt; und bei
Männern gibt es nicht mal mehr
zwei Möglichkeiten, sondern nur noch
eine:
 )
)
-
himmelhoch jauchzend
oder zu Tode betrübt,
-
friss
oder stirb,
-
"Ganz oder aber
gar nicht
das ist mein Prinzip.
Ganz oder aber
gar nicht
habe ich dich lieb."
(Gitte Haenning)
-
 ,
,
-
du hast die
Wahl zwischen Pest und
Cholera,
-
wer nicht
für uns ist, ist
gegen uns,
-
 ,
,
-
oder eben schwarz
oder weiß
(auch "Schwarzweißdenken" genannt):
"tertium non datur", d.h. eine
dritte
(oder gar vierte, fünfte ...)
Möglickeit
gibt es nicht, also

Solch zweiwertiges Denken macht die Welt natürlich
hübsch einfach
(auch einfach oder sogar überhaupt erst zu
berechnen)
und führt doch schnell zu
Betriebsblindheit - und
Fanatismus
(weshalb inzwischen sogar die
Mathematiker manchmal zu

[es gibt also angeblich drei
Kategorien: dreckig, sauber und rein]
übergehen).
|

|
jeder einzelne
Zuschauer guckt
entweder die Sendung
|
oder guckt sie
nicht
|
|
|
Es gibt also nicht
die Kategorien "guckt sie
manchmal"
oder "hat sie nur
einmal geguckt - und danach
nie wieder".
|
|

|
entweder gucken mehr
als 10% die Sendung (p
> 0,1)
|
oder es gucken
genau
10% oder
weniger die Sendung (p
≤
0,1)
|
|
|
Da bleibt im Intervall [0;1] kein
anderes p über.
|
|

|
es gibt die
Alternativhypothese
|
und die Nullhypothese
|
|
|
aber keine dritte
Hypothese.
|
|

|
jede der beiden Hypothesen hat einen
Annahmebereich
|
und einen Ablehnungsbereich
|
|
|
Beide Bereiche
überschneiden sich nicht, ergänzen
sich aber zur Gesamtmenge
{0, 1, 2 ... 200}, so dass kein Platz für einen
dritten Bereich übrig ist.
|
|

|
der Annahmebereich
der einen Hypothese
|
ist der Ablehnungsbereich
der anderen Hypothese
|
|
|
|
|

|
es gibt nur die Entscheidung, die neue
Staffel zu kaufen
|
oder sie nicht
zu kaufen
|
|
|
aber nicht die
Möglichkeit, sie z.B. teilweise zu
kaufen.
|
|

|
unser Hypothesentest ist entweder
richtig
|
oder falsch
(vgl.
 ) )
|
|
|
aber nicht z.B.
"ungefähr richtig".
|
|

|
solche mathematischen Überlegungen wie in diesem
Aufsatz interessieren einen
|
oder man findet sie allzu
lang(weilig) bzw.
hasst sie sogar.
|
"It don't matter
if you're black or white"
(Michael Jackson)
"Ebony and ivory
live together in perfect harmony"
(Paul McCartney & Stevie Wonder)
Wenn du auf ehrlichem Weg hierhin gelangt bist
(also nachdem Du brav den
ganzen Text durchgeackert
hast),
springe zur Belohnung
 hierhin.
hierhin.

Wenn Du trotz strengen Verbots sofort vom Anfang hierher gesprungen bist:

Selbstverständlich würde ich das Folgende niemals
vorweg verraten, denn das würde doch alle von der
vollständigen Lektüre des Textes abhalten, die
nie zuvor ist mir der Unterschied
(oben die mickrigen Passagen, die
schwarz eingerahmt sind)
und
Verstehen.jpg)
(der
Gesamttext)
so deutlich geworden wie bei der obigen langwierigen
Behandlung der anfangs zitierten Aufgabe:
(und doch ist handwerkliches Können unabdingbare Voraussetzung aller Kunst),
(überhaupt
kann man anhand eines einzigen, an sich
völlig uninteressanten Bespiels
[gibt es etwas Langweiligeres als Fernsehserien?!]
die
halbe
Welt verstehen).
Das
Rechnen
wird man später in den allermeisten Berufen nie
wieder brauchen
(zumindest nicht das
Berechnen von Hypothesentests),
aber
(und Gymnastik treibt man zwecks körperlicher [hier
geistiger] Fitness und
Wendigkeit, aber
nicht, um irgendwas zu "behalten")
ist ein Teil der Allgemeinbildung, der zum Erlangen der
"allgemeinen HochschulREIFE" verlangt werden darf - und sollte, weil die
Mathematik nun mal eine bedeutende und
(ob's einem gefällt oder nicht)
enorm wirkungsvolle
Kulturleistung ist.
Man kann natürlich auch streng nach dem Motto

-
nur stumpf die wenigen (unverstandenen!)
Rechenschritte in sich reinpauken,
-
damit halbwegs die nächste Klausur und eine
eventuelle Abiprüfung überleben
-
und dann alles so schnell wie möglich
vergessen.
 strengstens
verboten!
strengstens
verboten!
![]() )
)








 )
)




 "
" )
) ,
, ,
,




.jpg)

.jpg)

.jpg)

