Hypothesentests oder
keine Ahnung, aber / deswegen guter Unterricht?
Aufgrund merkwürdiger Umstände wurde ich gebeten, am Folgetag an einer anderen (nicht "meiner") Schule eine Vertretungsstunde in einem 12er Mathematikkurs abzuhalten, und zwar zum allseits beliebten Thema "Hypothesentests".
Eine entsprechende Aufgabe, die die SchülerInnen zu dieser Stunde lösen sollten, samt Lösungszettel hatte ich vom zu vertretenden Fachlehrer erhalten, aber da dachte ich mir doch:
abgesehen davon, aus dem Netz eine Beispielaufgabe zu "Alternativtests" herunterzuladen (allererster Google-Treffer), tue ich gar nichts, bereite mich also bewusst mal nicht auf die Stunde vor, sondern mache die SchülerInnen zu "Experten" und lasse mir von ihnen alles verklickern.
Hypothesentests hatte ich das letzte Mal vermutlich
- im Studium beim Thema "Stochastik" und
- in einer der ersten Mathe-Fachseminarstunden im Referendariat
(welch schwachsinnige Idee, ein Referendariat ausgerechnet damit anzufangen!)
durchgenommen. Zur fraglichen Stunde hatte ich also Vorkenntnisse, die wohl eher von unten gegen Null konvergierten.
Und erstens kommt es anders, und zweitens als man denkt:
keinE EinzigeR der SchülerInnen hatte die Aufgabe lösen können, ja, keinE EinzigeR hatte auch nur ansatzweise verstanden, wie man vorgehen könnte.
Und der Lösungszettel war ebenfalls für keineN EinzigeN hilfreich.
(Wohlgemerkt, es liegt mir völlig fern, das auf den zu vertretenden Lehrer [den ich nicht mal kenne] zurückzuführen, sondern
- ist die Stochastik nicht für SchülerInnen, sondern "sogar" auch für LehrerInnen ein ungewohntes und schwieriges Gebiet,
- sind insbesondere Hypothesentests schwierig.
Ebenso wenig mache ich den Aufgaben- und LösungsautorInnEn irgendwelche Vorwürfe: es ist halt verdammt schwer, mit notgedrungen wenigen Sätzen für Verständnis zu sorgen, zumal SchulbuchautorInnEn nicht auf individuelle oder kursspezifisch Probleme reagieren können.)
Hier also zu erstmal die Aufgabe:
- "Eine Agrargenossenschaft erhält mehrere Container mit Saatgetreide. Bestellt waren zwei Sorten: Während die eine Sorte eine Keimfähigkeit von 90% besitzt, dafür aber anfälliger gegenüber Schädlingen ist, keimt die andere nur in 75% der Fälle, ist aber gegenüber einem Schädlingsbefall resistenter. Aus der Beschriftung der angelieferten Container ist allerdings nicht mehr zu ersehen, welches Saatgetreide sich in welchem Container befindet. Es soll der Inhalt eines bestimmten Containers mithilfe einer Stichprobe von 100 Getreidekörnern untersucht werden, indem man diese Getreidekörner in einem Gewächshaus zum Keimen bringt."
Nun wusste ich ja (vielleicht anders als die SchülerInnen), dass "eingekleidete" Aufgaben sich ähneln wie ein Ei dem anderem, und deshalb fiel mir auch prompt die entlarvende bzw. erhellende Ähnlichkeit zu der Aufgabe auf, die ich aus dem Internet gezogen hatte:
-
"Eine Fabrik liefert Schachteln mit Schrauben hoher Qualität (10% der Schrauben sind fehlerhaft) und minderer Qualität (40% fehlerhaft) an eine Baumarktkette.
Während des Ausladens geht bei einigen Verpackungen das Etikett ab. Da man nicht weiß, ob es sich um Schrauben 1. oder 2. Wahl handelt, muss ein Verfahren gefunden werden die Schrauben in kürzester Zeit der richtigen Qualität zuordnen zu können.
Weiter sei gegeben, dass sich in jeder Schachtel 300 Schrauben befinden."
(Quelle:  )
)
Um die parallele Struktur zu verdeutlichen, seien mal beide Aufgaben neben einander gestellt:
| 1. | 2. |
| "Eine Agrargenossenschaft erhält mehrere Container mit Saatgetreide. Bestellt waren zwei Sorten: Während die eine Sorte eine Keimfähigkeit von 90% besitzt, dafür aber anfälliger gegenüber Schädlingen ist, keimt die andere nur in 75% der Fälle, ist aber gegenüber einem Schädlingsbefall resistenter. | "Eine Fabrik liefert Schachteln mit Schrauben hoher Qualität (10% der Schrauben sind fehlerhaft) und minderer Qualität (40% fehlerhaft) an eine Baumarktkette. |
| Aus der Beschriftung der angelieferten Container ist allerdings nicht mehr zu ersehen, welches Saatgetreide sich in welchem Container befindet. | Während des Ausladens geht bei einigen Verpackungen das Etikett ab. |
| Es soll der Inhalt eines bestimmten Containers mithilfe einer Stichprobe von 100 Getreidekörnern untersucht werden, indem man diese Getreidekörner in einem Gewächshaus zum Keimen bringt." | Da man nicht weiß, ob es sich um Schrauben 1. oder 2. Wahl handelt, muss ein Verfahren gefunden werden die Schrauben in kürzester Zeit der richtigen Qualität zuordnen zu können. |
| | Weiter sei gegeben, dass sich in jeder Schachtel 300 Schrauben befinden." |
Offensichtlich handelt es sich - zumindest mathematisch gesehen - um fast identische Aufgaben: das mathematische Grundproblem ist nur verschieden "verpackt" worden, d.h. letztlich ist es völlig unerheblich, ob es sich um Getreidekörner oder um Schrauben handelt und ob sie (nicht) keimfähig oder aber - allgemeiner gesagt - (nicht) fehlerhaft sind.
(Was einerseits auf Phantasielosigkeit hinzudeuten scheint, kann man andererseits aber auch mal positiv sehen: es ist doch auch schön, dass einige wenige mathematische Gleichungen ausreichen, um mittels ihrer gleich massenhaft Anwendungsbeispiele zu "erschlagen". Gerade das macht ja die "Anwendungsmathematik" überhaupt aus und hat ihren Siegeszug quer durch alle Naturwissenschaften und Technik begründet.)
Zudem ist in der 1. Aufgabe am Ende nur nach den keimfähigen Getreidekörnern, nicht aber nach den resistenteren gefragt. D.h. die Zusatzangabe "gegenüber einem Schädlingsbefall resistenter" (wozu ja auch keinerlei Zahlen vorliegen) ist für die Lösung der Aufgabe völlig irrelevant
(und macht die Aufgabe doch realistischer: vermutlich muss man einen Kompromiss zwischen Keimfähigkeit und Resistenz finden, der aber eben nicht mehr mathematisch bestimmbar ist;
dieses realistische Argument fehlt aber völlig in der 2. Aufgabe, in der dafür en völlig absurder Wert auftaucht: 40 % fehlerhafte Schrauben, das ist nicht mehr normaler Ausschuss, sondern schlichtweg Ramsch bzw. Betrug).
Man könnte die beiden Aufgaben also folgendermaßen reduzieren:
1.
| 2.
|
1. Wert 90 %
2. Wert 75 % | 1. Wert 10 %
2. Wert 40 % |
| auf Anhieb unklar, welcher Wert vorliegt | auf Anhieb unklar, welcher Wert vorliegt |
Oben war bereits gesagt worden, die beiden Aufgaben seien "fast" identisch. Aber eben auch nur "fast", denn es gibt auch klare Unterschiede:
| 1. | 2. |
| ein einziger Container soll untersucht werden | Verfahren offen
(evtl. mehrere Packungen?) |
Stichprobengröße vorgegeben
(100) | Stichprobengröße noch nicht genannt |
Packungsgröße unbekannt
(in einen Container passen abermilliarden Getreidekörner?) | in jeder Packung sind 300 Stück |
Diese nur scheinbar kleinen Unterschiede haben aber durchaus gravierende Folgen:
| 1. | 2. |
| ein einziger Container soll untersucht werden | es soll vermutlich ebenfalls eine einzige Packung untersucht werden |
Stichprobengröße vorgegeben
(100) | die Frage ist, welche Stichprobengröße sinnvoll ist |
| wegen der enorm großen Grundmenge kann man von "Ziehen mit zurücklegen" ausgehen. | wegen der nur 300 Stück großen Grundmenge muss von "Ziehen ohne zurücklegen" ausgegangen werden |
Das hat mit Eigenlob gar nichts zu tun: ganz offensichtlich bringe ich eben doch zwei Arten von Vorwissen mit:
- die Fähigkeit, Matheaufgaben zu strukturieren und das Wesentliche (Mathematische) vom Unwesentlichen zu trennen;
- das Wissen, dass die meisten Schul-Matheaufgaben nur verschiedene Verpackungen ein und desselben Inhalts sind: d.h. ich lasse mich nicht durch Getreide, Schrauben o.ä. irritieren,
- das Wissen um prinzipielle Unterschiede (mit/ohne zurücklegen).
Alle drei Punkte müssen aber mit SchülerInnen schon allein der Fairness halber geübt werden.
| In beiden Aufgaben geht es darum, nicht die Gesamtmenge (den ganzen Container, die ganze Schachtel), sondern jeweils nur eine (relativ kleine) Stichprobe zu untersuchen (diese Stichprobe wird ja nur in der 1. Aufgabe ausdrücklich erwähnt, während sie in der 2. Aufgabe mit "in kürzester Zeit" nur angedeutet ist). |
Nur bei einer Stichprobe (einem Teil der Gesamtmenge) kommt ja die Stochastik ins Spiel: wenn man hingegen die Gesamtmenge untersucht, hat man ja die absolute Sicherheit, welche Art Getreide/Schrauben in dem Container/der Schachtel ist.
| Die Frage bei der jeweiligen Stichprobe ist aber, - mit welcher Berechtigung man auf die Gesamtmenge schließen kann und
- bei welchen Stichprobenergebnissen man wie auf die Gesamtmenge schließt.
| |
Ein Beispiel zur Aufgabe 1.: angenommen, von den 100 gezogenen Getreidekörnern erweisen sich z.B. 82 [s.u.] als keimfähig. Spricht das eher für die bessere oder eher für die schlechtere Getreidesorte? Wohlgemerkt: "spricht das eher", denn absolute Sicherheit hat man natürlich nicht, da das Ergebnis 82 sowohl bei Containern mit guter als auch solchen mit schlechter Keimfähigkeit möglich ist. Ganz anders scheint das Problem hingegen in der 2. Aufgabe zu liegen: da ist ja nicht die Stichproben-, sondern die Gesamtmengengröße vorgegeben (300 Schrauben). Hier scheint also die Frage zu sein: wie groß sollte ich überhaupt eine Stichprobe wählen, um eine halbwegs sinnvolle Hypothese über die Qualität der Schrauben in der Gesamtschachtel machen zu können?
| Man wird schon raushören: was heißt eigentlich "sinnvoll" (bzw. "Berechtigung"), und ist das überhaupt mathematisch entscheidbar? |
Im Folgenden behandle ich nur die 1. Aufgabe weiter: da ich keinen blassen Schimmer mehr hatte, wie diese Aufgabe rechnerisch zu lösen war, und da mir die SchülerInnen da auch nicht helfen konnten, haben wir einfach zum Lösungsblatt gegriffen:

Dieser Text aber, an dem es an sich nichts zu kritisieren gibt, sondern der ja nur versucht, zur mathematischen Lösung hinzuführen, statt sie nur einfach fix und fertig "hinzuknallen", war für die SchülerInnen vollends unverständlich: sie konnten schon gar nicht die mathematische Quintessenz herausfiltern, weil sie
- vermutlich vor lauter Bäumen nicht mehr den Wald
- und vor lauter Vorinformationen nicht das Signal- und Gelenkwort "reduziert sich jetzt" erkannten.
Nach diesem Signal- und Gelenkwort folgt also das mathematisch eigentlich Wichtige, das erstaunlich knapp und einfach (?) ist.
Oder anders gesagt:
lange (Vor-)Rede, kurzer (mathematischer) Sinn:
(Nebenbei: in dieser Textpassage wird zwar kurz von "verschiedene[n] Überlegungen" gesprochen, irritierenderweise dann aber [in der nächsten Zeile] nur eine einzige ausgeführt.)
für mich war damit schlagartig klar:
- nimmt man sowieso den "oberen" Bereich k2 von 90 bis 100, also
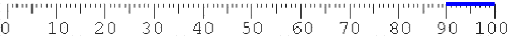
- berechnet man den "unteren" Bereich k1 mittels der ominösen Formel
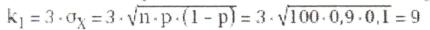
zu 9, erhält also als Gesamt-Entscheidungsbereich für die gut keimfähige Getreidesorte
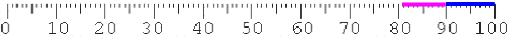
(Nebenbei: ominös ist die Formel nur, wenn man
-
übersieht, dass es sich um eine Binomialverteilung handelt, und
-
noch nicht weißt, dass sich bei Binomialverteilungen die Standardabweichung nach der hier vorliegenden, letztlich sehr einfachen Wurzel-Formel berechnet.)
Bzw. in Worten:

Bemerkenswert daran ist: wenn man noch gar nicht weiß, um welche Getreidesorte es sich handelt, startet man in diesem Fall mit der Vorweg-Hypothese, dass es sich um die 90-%-Sorte handelt, und entscheidet sich nach Ziehen der Stichprobe
- im lila-blauen Bereich für die Sorte mit der besseren Keimfähigkeit
- und im grünen Bereich für die Sorte mit der schlechteren Keimfähigkeit:

(Es scheint nebenbei, dass wir immer nur die gut keimfähigen Körner in der Stichprobe messen, und zwar unabhängig davon, ob unsere Anfangshypothese für den Gesamtcontainer "gut keimfähig" oder "schlecht keimfähig" lautet.)
Weil man aber vorweg nicht weiß, um welche Sorte es sich handelt, hätte man genauso gut mit der 75-%-Hypothese anfangen können, und es ergäbe sich mit analoger Argumentation:
- nimmt man sowieso den Bereich k1 bis 75, also

- berechnet man k2 mittels der Formel

Nun gilt 75 + 12,99 = 87,99. Da aber nur ganze Zahlen von Getreidekörnern auftauchen, wählen wir den zweiten Bereich k2 bis 87 und erhalten insgesamt:

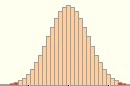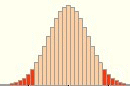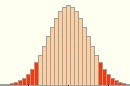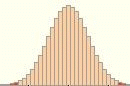
Wenn in diesem Fall also die Stichprobe zwischen 0 und 87 gut keimfähige Getreidekörner enthält, wird man sich dafür entscheiden, dass der Gesamtcontainer dennoch schlecht keimfähige Getreidekörner enthält. Wenn aber die Stichprobe zwischen 88 und 100 gut keimfähige Getreidekörner enthält, wird man sich dafür entscheiden, dass auch der Gesamtcontainer gut keimfähige Getreidekörner enthält.
Kleiner, in der entsprechenden Stunde nicht angesprochener Exkurs:
Auf den ersten Blick erstaunlich und allemal bemerkenswert ist, dass die beiden Bereiche für die Hypothese 75 % und 90 % sich nicht - wie man naiverweise doch erwarten würde - exakt ergänzen, sondern im Bereich [81, 87] überlappen:

Was also, wenn in unserer Stichprobe z.B. 82 gut keimfähige Getreidekörner sind? Dann müssen wir uns an unsere Anfangshypothese halten:
- Anfangshypothese 75 % Keimfähigkeit, 82 gut keimfähige Getreidekörner
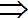 Anfangshypothese 75 % bestätigt
Anfangshypothese 75 % bestätigt  guter Container
guter Container - Anfangshypothese 90 % Keimfähigkeit, 82 gut keimfähige Getreidekörner
 Anfangshypothese 90 % nicht bestätigt
Anfangshypothese 90 % nicht bestätigt  schlechter Container.
schlechter Container.
Trotz der einheitlichen Zahl von 82 guten Getreidekörnern treffen wir also je nach Anfangshypothese völlig unterschiedliche Entscheidungen, d.h. die Anfangshypothese schränkt unsere spätere Entscheidung massiv ein.
Und es sei nochmals betont: unsere spätere Entscheidung kann dennoch falsch sein, der Container also sehr wohl "gut" sein, obwohl wir auf einen "schlechten" geschlossen hatten - und umgekehrt.
Fragt sich nur, wie es - gegen allen gesunden Menschenverstand - dazu kommen kann, dass in

die Überschneidung zustande kommt.
Das liegt daran, dass zwar beides Mal dieselbe Formel
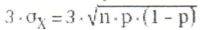
benutzt, aber für p doch völlig unterschiedliche, nicht zusammenhängende Werte eingesetzt werden (einmal 0,9, das andere Mal 0,75).
Interessant wären zwei Fragen, von denen die zweite hier allerdings nur angedeutet werden soll:
- Wann ist
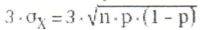 in beiden Fällen (für beide p) gleich. Doch offensichtlich, wenn das eine p gleich 1 minus dem anderen p ist.
in beiden Fällen (für beide p) gleich. Doch offensichtlich, wenn das eine p gleich 1 minus dem anderen p ist.
Formulieren wir dazu die 1. Aufgabe mal teilweise um
(überhaupt lohnt es sich ja immer, mit symmetrischen und Extremwerten zu arbeiten): - unverändert keimen 90 % des guten Getreides, und bei der 90%-Hypothese ergibt sich, wie oben gezeigt,

wobei 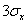 =
=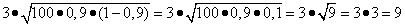
- beim schlechten Getreide sollen nun aber nur 10 % keimen. Damit ergibt sich ebenfalls
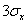 =
=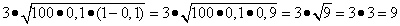 ,
,
so dass sich in diesem Fall ergibt:

Legen wir nun die beiden Strahlen übereinander, so ergibt sich der merkwürdige Effekt, dass sich die beiden Entscheidungsbereiche in einem sehr breiten Bereich nicht überschneiden:

Was bedeutet das?: dass wir uns - egal bei welcher Anfangshypothese (10% oder 90 %) - wahrscheinlich immer "verhauen", dass also unsere Entscheidungen äußerst schwach begründet sind?
- Und all das schreit nach der Folgefrage, in welchen Fällen sich die beiden Entscheidungsbereiche exakt ergänzen, also ohne sich zu überlappen.
Damit aber zurück zum oben erarbeiteten Lösungs"system":
Nach diesem von mir herausgearbeiteten System konnten die SchülerInnen nun aber mit Leichtigkeit andere, analoge Aufgaben durchrechnen.
Fragt sich nur, ob ich das System überhaupt richtig verstanden hatte.
Deshalb haben wir am Ende der Stunde drei Fragen erarbeitet, die dem regulären Lehrer, der sicherlich besser im Stoff steht, in einer der Folgestunden gestellt werden sollten:
- Ist das System überhaupt richtig verstanden und angewandt worden?
- Wann muss man den
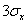 -Test anwenden und wann den (anderweitig in der Aufgabenlösung erwähnten)
-Test anwenden und wann den (anderweitig in der Aufgabenlösung erwähnten) 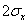 -Test? Ist das willkürlich?
-Test? Ist das willkürlich? - Wann muss man "mit" und wann "ohne zurücklegen" bedenken? - und was ändert sich dann an der erarbeiteten (richtigen?) Standardrechnung?
Inzwischen wird man sich aber fragen dürfen, was an solchem Unterricht überhaupt "gut" gewesen sein soll.
War er aus mehreren Gründen nicht sogar miserabel schlecht?:
- war der Lehrer (ich) nicht vorbereitet und hatte keinerlei Ahnung. Wie soll der den SchülerInnen da irgendwas "beibringen"?
- Besteht nicht die Gefahr, dass er ihnen etwas Falsches beibringt und das trotz späterer Korrektur durch den regulären Fachlehrer hängen bleibt?
- ist offensichtlich das (naive?) Konzept, die SchülerInnen zu "Experten" zu machen und sich alles von diesen erklären zu lassen, von Anfang an gründlich gescheitert.
- bleibt für mich (und die SchülerInnen?) ungeklärt, was überhaupt die Formel
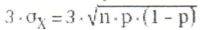 bedeutet bzw. wie man auf sie kommt.
bedeutet bzw. wie man auf sie kommt.
(Aber ich habe jetzt natürlich "Blut geleckt" und werde das Verständnis dieser Formel nachholen.)
Ich glaube dennoch, dass die entsprechende Schulstunde einen enormen Vorteil hatte:
die SchülerInnen konnten immerhin mal dabei zuschauen, wie ein Lehrer (ich) sich selbst in ein ihm weitgehend unbekanntes Gebiet einarbeitete.
Oder anders gesagt: endlich sind mal nicht mehr nur immer die SchülerInnen die Doofen!
Denn ich halte es sogar für fatal, dass LehrerInnen immer alles (besser) wissen, denn dadurch werden sie doch allzu leicht betriebsblind für Anfängerprobleme.
Noch ein Problem scheint mir erwähnenswert:
darf man den langen, Hintergrundverständnis erzeugenden (?) Text

so einfach auf die reine Mathematik
also auf reine (unverstandene, aber anwendbare) Rechenrezepte reduzieren???
Ist das nicht der Tod jeder "Verständnis"-Mathematik und spielt das nicht der modischen puren Abprüfbarkeit in die Hände?
Mir scheint beides wichtig:
- einerseits brauchen die SchülerInnen dringend Sicherheit, also eben auch stumpf anwendbare Rechenregeln,
- andererseits fängt die eigentliche (auch zu vermittelnde!) Mathematik überhaupt jenseits der Rechenregeln an bzw. erst mit ihrer Herleitung und ihrem tieferen Verständnis.
Umgekehrt: sagt der Lösungstext mit dem Signalwort "reduziert sich jetzt" sogar selbst, dass alles vorher überflüssiger Luxus war?
Zur Fortsetzung siehe
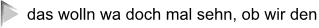

![]() )
)



