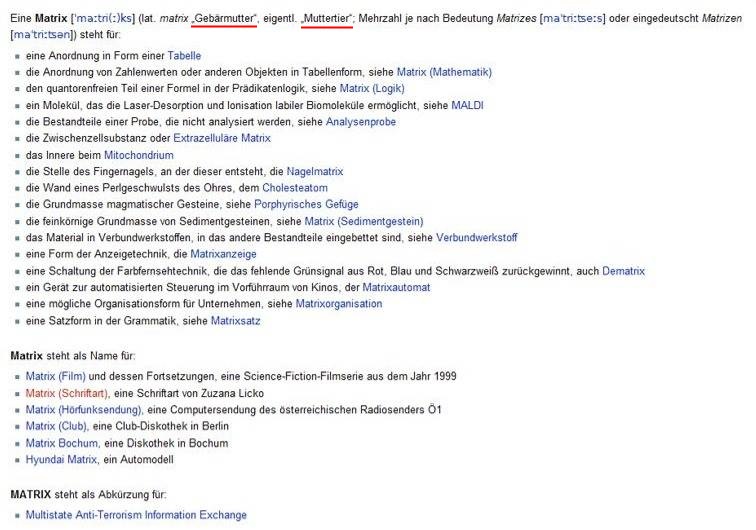
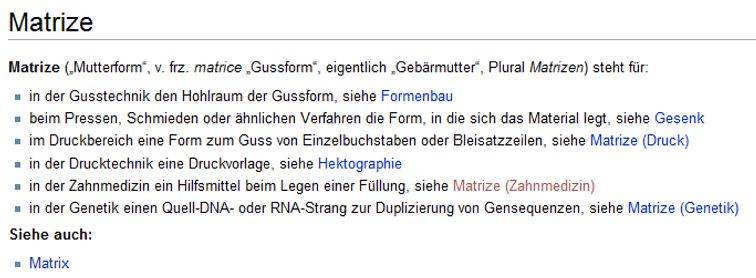
Wenn die Matrix die Gebärmutter
bzw. das Muttertier ist,
so ist sie sozusagen der (mathematische) Ursprung von allem:
"Der heutige Spieß wird oft
als Mutter der Kompanie bezeichnet.
Diesem Namen soll er dadurch gerecht werden,
dass er seinen Soldaten ein vertrauenswürdiger Ansprechpartner und
Berater,
zugleich aber auch Ermahner und Zurechtweiser sein soll."
(Quelle: ![]() )
)
Diese häufige Verwendung des Wortes "Matrix" bzw. "Matrize" wundert mich ja doch. Könnte es dafür folgende Gründe geben?:
- nur der Wortklang
(wo doch vermutlich viele gar kein Altgriechisch können und wohl auch nicht die mathematische Bedeutung der Matrix kennen)?
- , dass die (durchaus mathematische) Matrix Inbegriff der
- Wissenschaftlichkeit

- Vieldimensionalität (s.u.), Wechselwirkungen und "Ganzheitlichkeit" ist?:

(Buchbesprechung in "Stern", 18.2.10)
- , dass die
 "Archetypen" Gebärmutter und Muttertier ganz
besonders als
"Archetypen" Gebärmutter und Muttertier ganz
besonders als 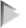 "conceptual metaphors" geeignet sind?
"conceptual metaphors" geeignet sind?
Vgl. aber beispielsweise auch
![]()
 .
.
Der Film
![]()
 , aus dem der Filmausschnitt
, aus dem der Filmausschnitt
stammt, und seine Fortsetzungen 
 sind zwar nicht meine Art Kino, aber es
lässt sich wohl kaum bestreiten, dass die Macher dieser Filme, nämlich
die Brüder Wachowski, mit allen intellektuellen Wassern gewaschen sind
sind zwar nicht meine Art Kino, aber es
lässt sich wohl kaum bestreiten, dass die Macher dieser Filme, nämlich
die Brüder Wachowski, mit allen intellektuellen Wassern gewaschen sind
(vgl. nur etwa das Buch  ).
).
Obwohl es im Filmausschnitt
"dummerweise ist es schwer, jemandem zu erklären, was die Matrix ist"
(man beachte das "die" im Sinne von "die wichtigste" bzw. "die spezifische im Film")
heißt, wird dann doch eine (relativ) leicht verständliche Erklärung gegeben:
Die "Matrix" ist also in diesen Filmen eine vergangene (unsere) Welt, die in der Zukunft nur noch in Form einer
(das hört sich ganz toll an, obwohl "Interaktivität" doch meist nur "new speak" für die Wahl zwischen den vorgegebenen Alternativen Pest und Cholera ist)
"neurointeraktiven Simulation" existiert, was vermutlich heißt: diese Simulation kann Menschen vorgespielt bzw. in ihrem Kopf erzeugt werden.
So an den Haaren herbeigezogen ist das gar nicht, sondern sowas wird ja inzwischen durchaus von einigen Computerfuzzis erträumt:
"Dann wird es auch
möglich sein, sein [= eines Menschen] Wesen in eine reine Maschine zu
kopieren, die sich dann ebenso verhält wie er. Die Maschine besitzt
dann sein Bewußtsein, ihr Bewußtsein ist unsterblich geworden. Hat eine
solche Maschine nun ein eigenes Bewußtsein?"
(Quelle: ![]() )
)
Und auch die Cyberpunks haben sowas schon er(alb)träumt:

(Wohlgemerkt: eine "neuroaktive Simulation" ist nicht mit Platons oder Descartes' prinzipiellem Zweifel an der Wirklichkeit zu verwechseln. Sondern bei der "Matrix" in den Filmen wird ja vorausgesetzt, dass es die Welt, die sie simuliert, tatsächlich mal gab:
Solange Computer aber konventionell funktionieren, also nur mit Zahlen hantieren können, ist die mathematische Matrix vermutlich die beste Speichermöglichkeit für eine große Ansammlung von teilweise miteinander in Beziehungen stehenden "Items":
„Im kommenden Jahrzehnt wird jeder von uns - oft
unwissentlich - in jedem Lebensbereich Modelle seiner selbst entstehen
lassen. Wir werden als Arbeitende, Patienten, Soldaten, Liebende,
Käufer und Wähler Modell stehen. Im jetzigen frühen Stadium sind viele
der Modelle noch primitiv und lassen uns wie Strichmännchen aussehen.
Doch das Endziel ist es, Modelle von Menschen zu entwickeln, die ebenso
komplex und einzigartig sind wie wir selbst. Betrachtet man all diese
Bestrebungen in ihrer Gesamtheit, so erleben wir die mathematische
Simulation der Menschheit. Diese Entwicklung verspricht eine der großen
Umwälzungen des 21. Jahrhunderts zu werden. Ihre Dimensionen werden
zunehmen und viele Bereiche der physischen Welt umfassen, wenn
Mathematiker sich neue Datenströme erschließen, etwa aus Netzwerken
atmosphärischer Sensoren oder den Videobildern aus Millionen
Überwachungskameras. Es entsteht eine Parallelwelt, ein Labor für
Innovationen und Entdeckungen, das sich aus Zahlen, Vektoren und
Algorithmen zusammensetzt. Und Sie und ich stecken mitten drin.
[...]
Die Numerati […] wollen für jeden Einzelnen von uns ein riesiges und
hochkomplexes Labyrinth aus Zahlen und Gleichungen berechen:
mathematische Modelle. Wissenschaftler setzen seit Jahrzehnten solche
Modelle ein, um alles Mögliche zu simulieren, von Lkw-Flotten bis hin
zu Atombomben. Sie bauen sie aus gewaltigen Datensammlungen zusammen,
deren Elemente Tatsachen oder Wahrscheinlichkeiten darstellen. […]
Komplexe Modelle können Tausende oder gar Millionen von Variablen
enthalten, deren mathematische Wechselwirkungen genau den Interaktionen
der wirklichen Welt entsprechen müssen. Die Entwicklung solcher Modelle
ist eine außergewöhnlich mühselige Arbeit, die große Sorgfalt
erfordert.“
(Quelle:  ; vgl. auch
; vgl. auch  )
)
Wenn man erstmal von eindimensionalen
Zahlen (z.B. 1) zu zweidimensionalen Vektoren (z.B. ![]() ) übergegangen ist,
liegt es innermathematisch nah, zu dreidimensionalen
) übergegangen ist,
liegt es innermathematisch nah, zu dreidimensionalen
![]() , vierdimensionalen
, vierdimensionalen
![]() und dann allgemein n-dimensionalen Vektoren
und dann allgemein n-dimensionalen Vektoren ![]() überzugehen:
überzugehen:

Wohlgemerkt: dabei geht es (noch) nicht um irgendeinen außermathematischen "Sinn", sondern höchstens um innermathematische "Konsistenz"
(darauf wird bei den Matrizen unten zurückzukommen sein).
Wenn man die Vektoren aber sukzessive nach unten erweitert hat, schreit das doch danach, sie im nöchsten Schritt auch seitlich zu erweitern
 ,
,
was sukzessive so aussehen könnte:
| |
→ | 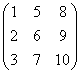 |
→ | 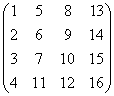 |
→ |  |
| 2 • 2 Dimensionen |
3 • 3 Dimensionen |
4 • 4 Dimensionen |
n • m Dimensionen |
Nun lasse man sich aber
mal auf der Zunge zergehen, was  "bedeutet":
"bedeutet":
- schon allein pro Spalte (Vektor) n, also beliebig viele Dimensionen
(dabei könne sich - s.u. - viele Menschen nicht mal vier Dimensionen vorstellen),
- und ebenso pro Zeile m, also beliebig viele Dimensionen,
- insgesamt also n • m, d.h. sozusagen "beliebig viele • beliebig viele" Dimensionen!
Vorstellen kann sich das wohl keiner, aber man kann
(wie wir unten sehen werden)
wunderbar damit rechnen.
Bislang haben wir aber all diese "beliebig viele • beliebig
viele" Dimensionen noch in der zweidimensionalen Matrix  dargestellt,
und das schreit doch wiederum danach, hier mal kurz ins Dreidimensionale,
also einen Quader, erweitert zu werden:
dargestellt,
und das schreit doch wiederum danach, hier mal kurz ins Dreidimensionale,
also einen Quader, erweitert zu werden:
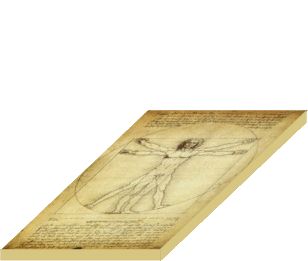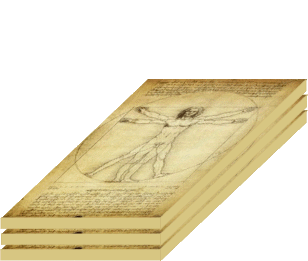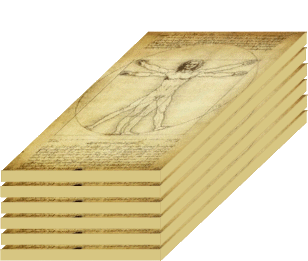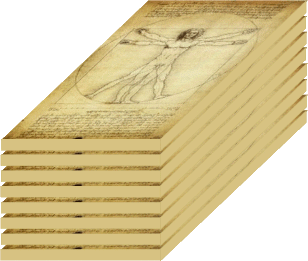

 ,
,
womit wir - schwups! - im n•m•k-, d.h. im "beliebig viel • beliebig viel • beliebig viel"-Dimensionalen sind.
Und wo wir schon bei so hübschen Verallgemeinerungen sind, geht's nun prompt ins Vierdimensionale

(was natürlich nur die zweidimensionale
Projektion eines vierdimensionalen Würfels,
also nur ein Abklatsch und Notbehelf ist),
Usw. usf.
(ins 5-, 6-, ... n-Dimensionale; vgl.
![]() )
)
- und keine Ahnung, was das "bedeutet".
Nun habe ich bereits zwei Mal "bedeutet" in Anführungszeichen geschrieben: es geht mir ja noch immer nicht um eine außermathematische (Anwendungs-)Bedeutung, sondern (vorerst) höchstens um eine innermathematische.
Aber selbst letztere sei vorerst noch zurückgestellt: vor allem geht es MathematikerInneN bei solchen Verallgemeinerungen, wie wir sie durchgeführt haben, um die oben bereits kurz erwähnte "innermathematische Konsistenz", was bedeutet: kann man mit solchen Matrizen wie
| |
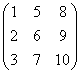 |
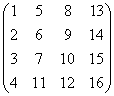 |
 |
rechnen - und wenn ja, wie?
Oder umgekehrt: lassen sich für Matrizen die üblichen Rechenoperationen ( + , - , • , : ) derart definieren, dass sie
- wenn irgend möglich in Analogie zu den bereits bekannten Rechenoperationen für Zahlen und Vektoren
(denn schließlich ist ein Vektor eine einspaltige Matrix, also "nur" ein Sonderfall der Matrix)
funktionieren oder - noch besser - auf diese zurückzuführen sind?
(Wir wollen ja nicht andauernd völlig neue Rechenarten lernen; vgl: zwei gleichnamige Brüche / Vektoren werden addiert, indem man ihre Zähler / Koordinaten [= hundsgewöhnliche ganze / sonstige Zahlen] addiert.)
- ist man natürlich erstmal frei in der Wahl, was beim Rechnen mit zwei Matrizen eigentlich rauskommen soll:
- eine Zahl (ein Skalar) wie beim Skalarprodukt zweier Vektoren?
- ein Vektor wie bei der s-Multiplikation eines Vektors mit einer Zahl (einem Skalar)?
- eine dritte Matrix?
- oder noch was ganz anderes?
Und wenn wieder eine Matrix herauskommen soll, so hätten die MathematikerInnen gerne eine "Gruppe":

(Quelle: ![]() ;
was sich hier so kompliziert anhört, ist uns z.B. bei der "additiven
Gruppe" der ganzen Zahlen geradezu selbstverständlich:
;
was sich hier so kompliziert anhört, ist uns z.B. bei der "additiven
Gruppe" der ganzen Zahlen geradezu selbstverständlich:
- wenn ich zwei ganze Zahlen addiere, kommt wieder eine ganze Zahl heraus;
- es gilt das Assoziativgesetz, also z.B. (2 + 3) + 4 = 2 + (3 + 4);
- die Addition von 0 verändert nichts;
- die Addition beispielsweise von 4 kann ich durch die Addition von - 4 rückgängig machen - und erhalte dadurch wieder 0,
was alles zusammen nur bedeutet, dass
- man keine bösen Überraschungen erleben, sondern "unter sich bleiben", also immer nur wieder ganze Zahlen bzw. Matrizen rausbekommen will:

- die simpelsten Rechengesetze gelten sollen
- und man alles jederzeit rückgängig machen können möchte.)
Die "Gruppe" ist eine Minimal- bzw. Schrumpfstruktur, bzw. die MathematikerInnen geben sich manchmal bereits mit relativ wenig zufrieden. So wird bei der "Gruppe" nichtmal Kommutativität gefordert (s.u.).
Auf dieses Rechnen mit Matrizen wird unten zurückzukommen sein, aber vorerst beschäftigen wir uns mit zwei anderen interessanten Aspekten:
- : was sollen denn mehr als drei Dimensionen bei Vektoren
(oder gar Matrizen)
bedeuten?
Innermathematisch ist das überhaupt keine Frage: die MathematikerInnen hantieren gerne mit Verallgemeinerungen, ohne sich darunter irgendwas vorstellen zu wollen.
Werden wir hier aber erstmals "außermathematisch":
bei einem Fußballspiel ist es nicht nur wichtig, dass der Ball im Tor landet
(also die räumlichen Koordinaten für Länge, Breite und Höhe stimmen),
sondern das muss auch während der Spielzeit passieren:
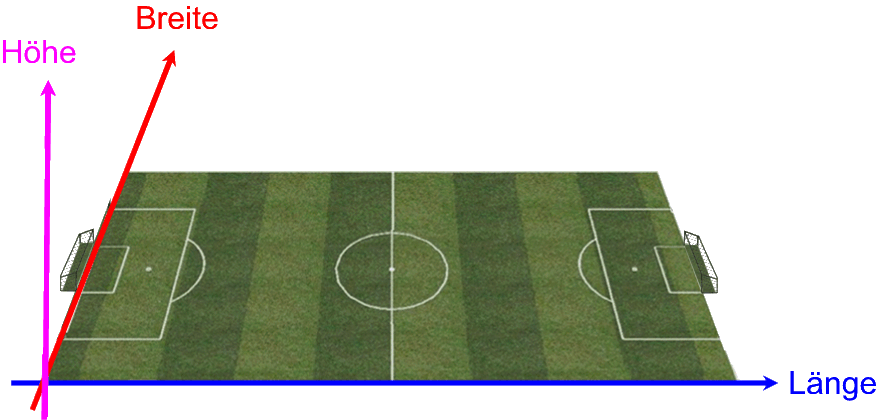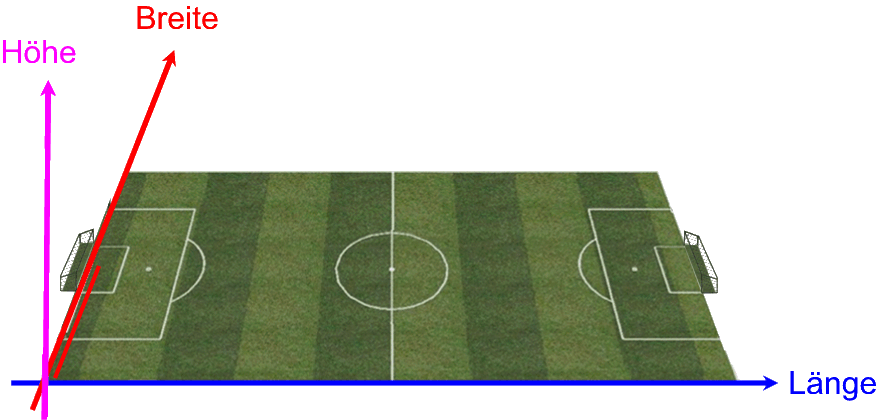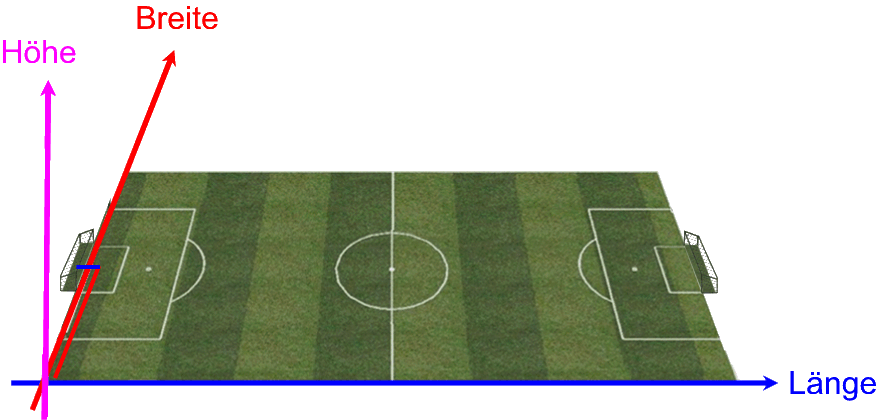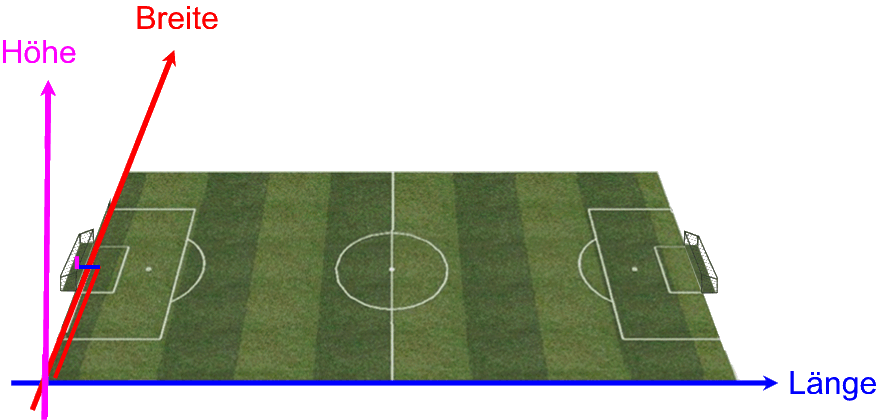
Hier ist es also sinnvoll, einen vierdimensionalen Vektor zu erstellen, nämlich z.B.
![]() ,
,
wobei
- - 1 bedeutet, dass der Ball hinter der Torlinie ist,
- 20, dass er auch "seitlich" passt, also nicht neben dem Tor vorbeifliegt,
- 1,5, dass er unterhalb der oberen Querstange des Tors landet, also nicht über ihm herfliegt,
- 43, dass das alles in der 43. Minute des Spiels oder überhaupt während der Spielzeit geschieht.
Das Raumzeit-Beispiel des Fußball-Treffers ist dreifach interessant:
- illustriert es sehr schön, dass die Hinzunahme einer vierten Dimension, nämlich hier der Zeit, durchaus sinnvoll sein kann,
- ist die Zeit für unseren "gesunden Menschenverstand" völlig unabhängig und abgetrennt von den drei Raumdimensionen;
- bestand Einsteins zentrale Erkenntnis in seiner
"allgemeinen Relativitätstheorie" aber gerade darin, dass Raum und Zeit "in
Wirklichkeit" keineswegs getrennt sind, sondern zusammengehören,
weshalb eben auch von der "
 "
"
(in einem Wort)
gesprochen wird:
![]()
Und im Grunde ist  auch nichts anderes als ein dreidimensionaler Würfel, der sich in der vierten Dimension (Zeit)
verändert.
auch nichts anderes als ein dreidimensionaler Würfel, der sich in der vierten Dimension (Zeit)
verändert.
Für sogenannte ![]() "String-Theoretiker" hat das Weltall eventuell sogar bis zu 26 (!?)
Dimensionen, die allerdings schlauerweise großteils "zusammengerollt"
sind.
"String-Theoretiker" hat das Weltall eventuell sogar bis zu 26 (!?)
Dimensionen, die allerdings schlauerweise großteils "zusammengerollt"
sind.
Und wie der "Numerati"-Auszug oben zeigt, versuchen Marktforscher sogar, hunderte von Konsumenteneigenschaften und -vorlieben in Vektoren zu packen
(und dann geheime Zusammenhänge [Korrelationen] zwischen ihnen zu finden)
.So kann man auch in unserem Fußballbeispiel natürlich noch
(mehr oder minder sinnvoll)
weitere Dimensionen hinzufügen, also z.B.
![]() ,
,
wobei
- 1 für Eigentor steht (2 würde "Fremdtor" bedeuten),
- 98 der Bauchumfang des Torschützen in cm ist.
Damit sind wir aber beim
- Aspekt, nämlich der Frage, wieso man die Vektoren
nicht einfach nur immer höher
 , sondern
auch breiter
, sondern
auch breiter  , also
zu Matrizen macht:
, also
zu Matrizen macht:
Es würde doch anscheinend reichen, beispielsweise die Matrix ![]() als
den Vektor
als
den Vektor ![]() zu schreiben: damit blieben die Informationen
"5" und "6" erhalten und würden nur unten an
zu schreiben: damit blieben die Informationen
"5" und "6" erhalten und würden nur unten an ![]() angehängt.
angehängt.
Wenn wir aber, wie oben gezeigt, die vierte
Dimension Zeit als völlig getrennt
vom den drei räumlichen
Koordinaten erleben, so scheint es umgekehrt sinnvoll, statt des Vektors
![]() doch lieber die matrizenähnliche
Schreibweise
doch lieber die matrizenähnliche
Schreibweise 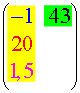 zu wählen.
zu wählen.
Eine Matrixschreibweise scheint also nur dann sinnvoll zu sein, wenn in den hinzukommenden Spalten ganz "andere" Dimensionen abgespeichert werden als in der ersten (Vektor-)Spalte.
Man könnte auch sagen:
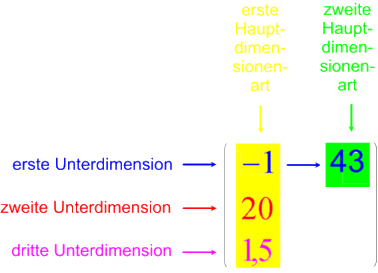
Nun wäre natürlich auch eine nicht-rechteckige Matrix-Definition möglich, also etwa
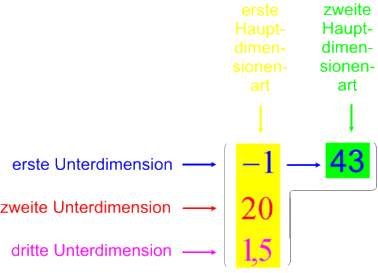
Wenn man aber eine rechteckige Matrize haben will
(warum das wünschenswert ist, werden wir unten an einem Anwendungsbeispiel sehen)
,so stellt sich natürlich die Doppelfrage:
- Was könnten die beiden Leerstellen ? und ? bedeuten?:
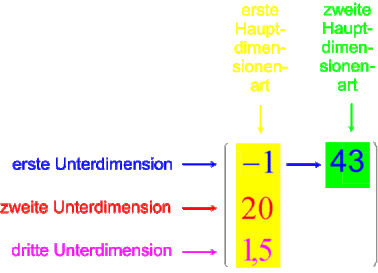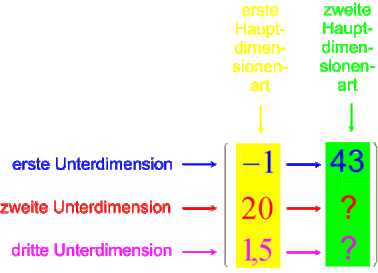
In unserem ![]() -Beispiel: gibt es noch
eine zweite und dritte,
für uns nicht wahrnehmbare Zeit-Unterdimension
-Beispiel: gibt es noch
eine zweite und dritte,
für uns nicht wahrnehmbare Zeit-Unterdimension
(insgesamt also sechs Unterdimensionen)
???Falls es aber diese zusätzlichen Zeit-Unterdimension gibt: ist es Zufall oder steckt ein naturwissenschaftliches Gesetz dahinter, dass es dann gleichviele Raum- wie Zeit-Dimensionen gibt?
Und wenn es weiteren Zeit-Unterdimension gibt:
- Gibt es Querverbindungen zwischen den nebeneinander stehenden Unterdimensionen
- -1 ↔ 43,
- 20 ↔ ? ,
- 1,5 ↔ ? ?
Nun sind aber die Raumdimensionen willkürlich angeordnet, d.h. man könnte von oben nach unten beispielsweise auch die Reihenfolge Breite, Höhe, Länge wählen. Das aber heißt doch, dass die Zeitdimension anscheinend zu keiner (einzelnen) der drei Raumdimensionen eine besondere Affinität hat. Es wäre also auch möglich:
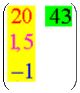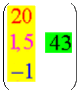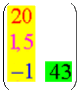
Zumindest beim ![]() -Beispiel sieht es also
so aus, dass es keine Querbeziehungen zwischen
nebeneinander stehenden Unterdimensionen gibt: jede
Spalte ist unabhängig von der/den anderen Spalte(n).
-Beispiel sieht es also
so aus, dass es keine Querbeziehungen zwischen
nebeneinander stehenden Unterdimensionen gibt: jede
Spalte ist unabhängig von der/den anderen Spalte(n).
Oben war schon angedeutet worden, dass wir die Matrizen gerne rechteckig haben wollen, d.h., dass es
- in jeder ihrer Spalten gleich viele Zahlen,
- in jeder ihrer Zeilen gleich viele Zahlen
geben soll. Bzw. eine Matrize entsteht dadurch, dass wir gleichlange Vektoren
- nebeneinander stellen
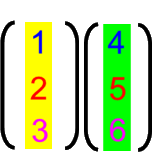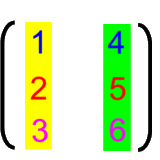
- oder übereinander
legen
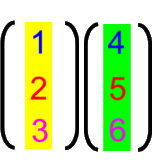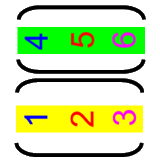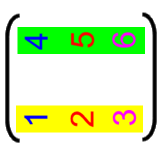 .
.
Kommen wir damit nun endlich zu einer anschaulichen Vorstellung von Matrizen:
angenommen, bei einem familiären Mittagessen gibt's Fischstäbchen mit Kartoffeln:
|
→ |
→  |
|
→ |
(Man beachte, dass die Essgewohnheiten der Kinder, also ![]() , nicht von denen der Erwachsenen, also
, nicht von denen der Erwachsenen, also ![]() , abhängig sind.)
, abhängig sind.)
Die Familie besteht aus
|
→ |
|
Bleiben wir aber zuerst bei den einzelnen Essensbestandteilen, also
- erst den Fischstäbchen,
- danach den Kartoffeln,
bevor wir beide Essensbestandteile zusammen betrachten.
Zu a., also den Fischstäbchen:
Erinnern wir uns vorweg, dass es zwei (genauer: drei) Arten der Vektormultiplikation gibt:
A. die s-Multiplikation, d.h.
- die Multiplikation
- eines Skalars (einer Zahl)
- mit einem Vektor;
- das Ergebnis ist ein verlängerter/verkürzter und eventuell "umgedrehter"" Vektorr:
Skalar mal Vektor = (neuer) Vektor
B. das Skalar-Produkt, d.h.
-
die Multiplikation
- eines Vektors
- mit einem (anderen) Vektor;
- das Ergebnis ist ein Skalar:
Dieses Skalarprodukt funktioniert beispielsweise so:
![]() •
• ![]() = 5 • 2 + 3 •
6 = 10
+ 18 = 28
= 5 • 2 + 3 •
6 = 10
+ 18 = 28
Und wenn wir den ersten Vektor ausnahmsweise mal quer legen, ansonsten aber nichts ändern, ergibt sich
![]() •
•
![]() = 5 • 2 + 3 • 6 = 10 + 18 = 28
= 5 • 2 + 3 • 6 = 10 + 18 = 28
Insgesamt werden in der Familie also 28 Fischstäbchen verzehrt.
Halten wir aber schon mal fest:
- in
 •
•
 muss der Vektor
muss der Vektor  natürlich
genauso "hoch" sein wie der Vektor
natürlich
genauso "hoch" sein wie der Vektor  ,
, - in
 •
•  muss der quergelegte Vektor
muss der quergelegte Vektor  genauso "breit" sein,
wie der Vektor
genauso "breit" sein,
wie der Vektor  "hoch" ist.
"hoch" ist.
Zu b., also den Kartoffeln: hier ergibt sich
(wieder mit dem Skalarprodukt)
analog zu a.
![]() •
• ![]() = 4 • 2 + 1 • 6 = 8 + 6 = 14
= 4 • 2 + 1 • 6 = 8 + 6 = 14
bzw.
![]() •
•
![]() = 4 • 2 + 1 • 6 = 8 + 6 = 14
= 4 • 2 + 1 • 6 = 8 + 6 = 14
Insgesamt werden in der Familie also 14 Kartoffeln verzehrt.
Und wieder ist festzuhalten:
|
|
Nun wollen wir gleichzeitig ermitteln, wieviele Fischstäbchen und wieviele Kartoffeln in der Familie insgesamt verzehrt werden.
Mit den obigen Einzelergebnissen für Fischstäbchen und Kartoffeln liegt es nahe, folgendermaßen vorzugehen:
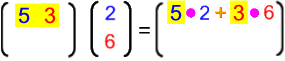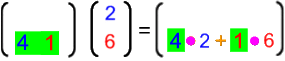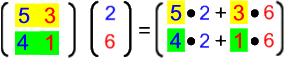
Offensichtlich funktioniert das insgesamt so:
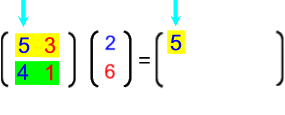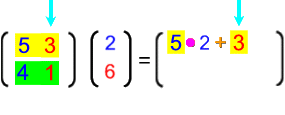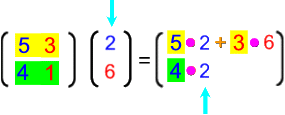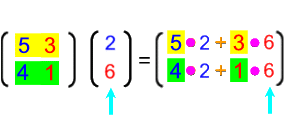
Oder vielleicht noch anschaulicher:
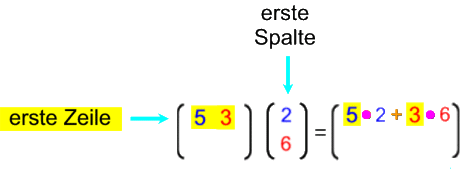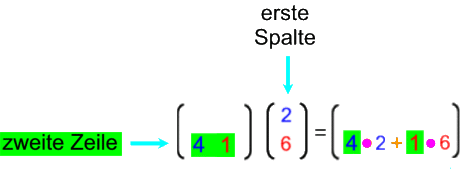
Da in den Rechnungen rechts massenhaft Multiplikationen stehen
(allerdings auch einige Additionen),
nennen wir auch das, was links geschieht, "Matrizenmultiplikation" und ergänzen dort deshalb ein Malzeichen:
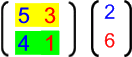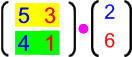
Genau genommen haben wir aber bislang nur
- eine 2 x 2 - Matrix, nämlich
 ,
, - mit einem Vektor, nämlich
 ,
,
multipliziert. Aber man kann den Vektor ja schon als eine 1 x 2 - Matrix ansehen. Vektoren sind - so gesehen - also nur besonders "schmale" Spezialfälle der Matrizen
(woraus folgt, dass die Rechenregeln für Matrizen auch für Vektoren gelten sollten, und wir hatten ja tatsächlich die Matrizenmultiplikation aus dem Skalarprodukt für Vektoren hergeleitet).
Um jetzt aber mal zwei "richtige" Matrizen miteinander zu multiplizieren, erfinden wir einfach eine zweite Familie,
- in der ebenfalls Fischstäbchen und Kartoffeln gegessen werden.
- Wir setzen dabei des weiteren voraus, dass alle Erwachsenen bzw. Kinder genauso viele Fischstäbchen und Kartoffeln essen wie in der ersten Familie,
- und ändern nur die Familiengröße: die zweite
Familie soll aus 3 Erwachsenen (Eltern +
Oma) und 5 Kindern bestehen, womit sich
als neuer "Familien-Vektor"
 ergibt.
ergibt.
Damit könnten wir analog zu oben  •
•
![]() rechnen, aber wir wollen im folgenden beide
Familien "in einem Abwasch" erledigen, rechnen also
rechnen, aber wir wollen im folgenden beide
Familien "in einem Abwasch" erledigen, rechnen also
 •
• 
Mit der oben hergeleiteten Multiplikationsregel ergibt sich
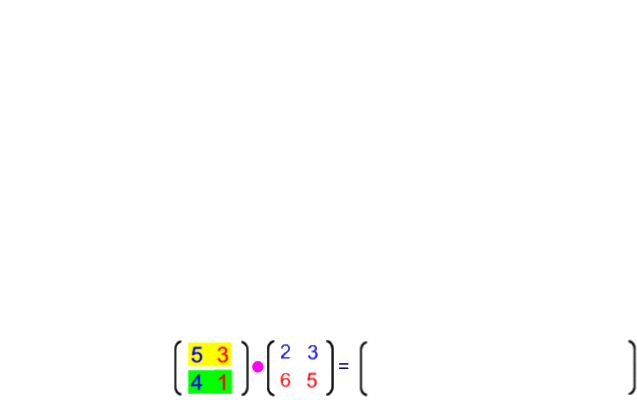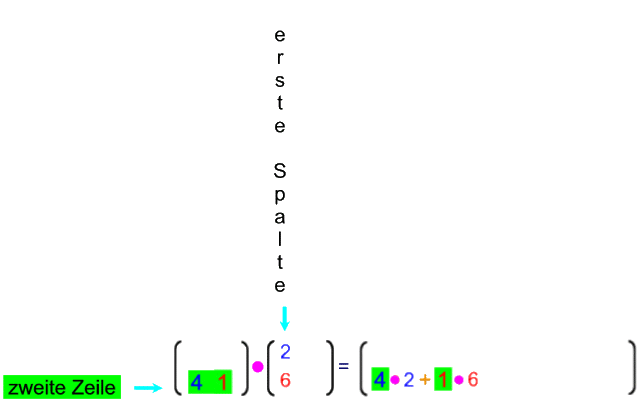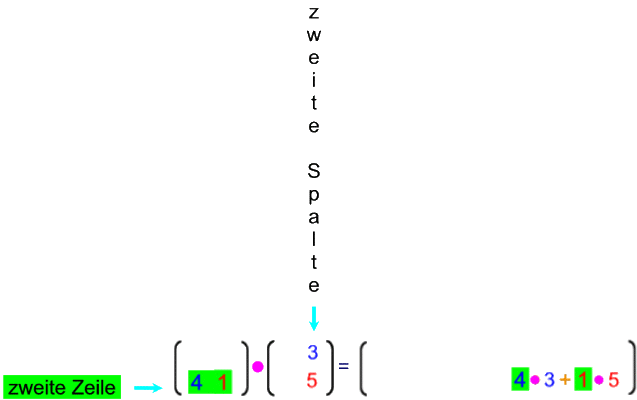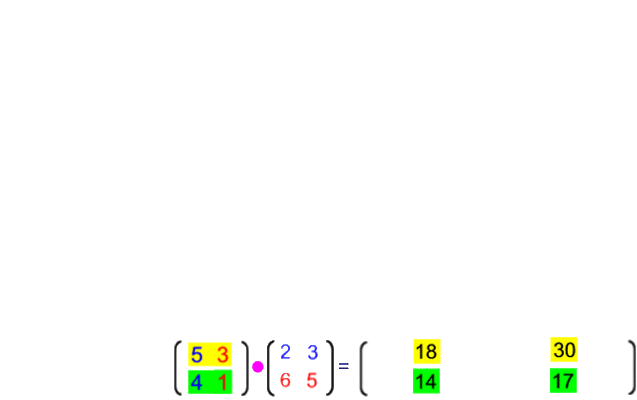
Schauen wir uns nun die Zusammenhänge genauer an:
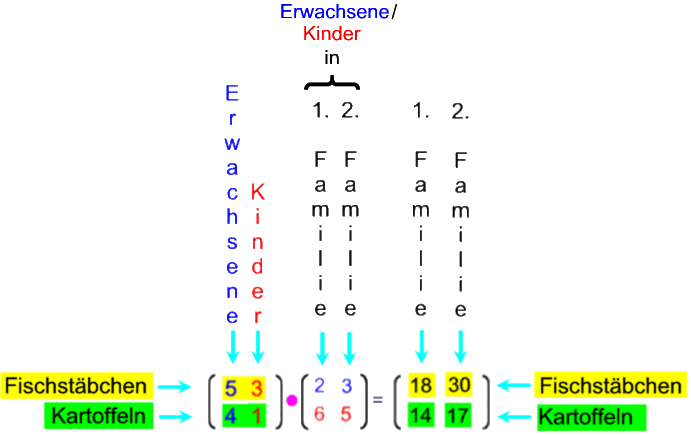
Und da ich mir ja zu keiner Veranschaulichung zu schade bin:

oder
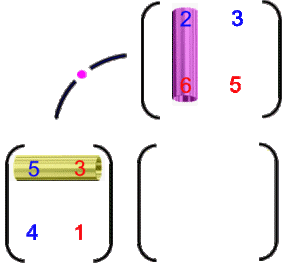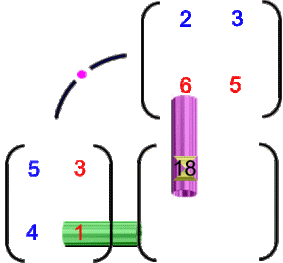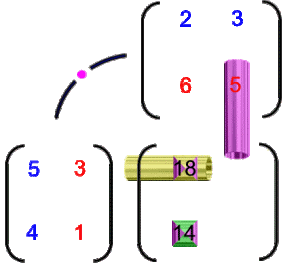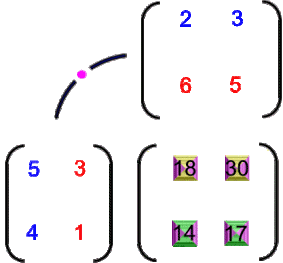
oder

Da all das notgedrungen ein bisschen klein geraten ist, hier noch vergrößert die Ausgangsmultiplikation:
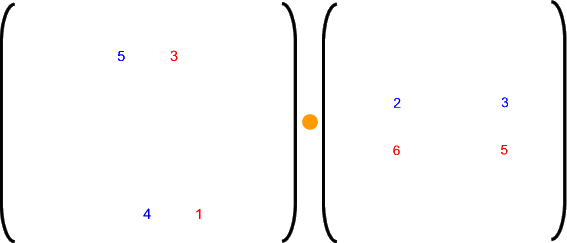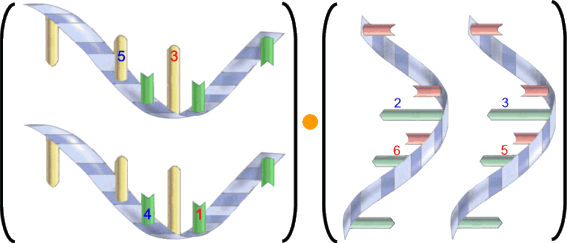
Bei all dem ist
-
 die "Verteilungs-Matrix":
sie zeigt an, wie viele Fischstäbchen
bzw. Kartoffeln die Erwachsenen
bzw. Kinder essen,
die "Verteilungs-Matrix":
sie zeigt an, wie viele Fischstäbchen
bzw. Kartoffeln die Erwachsenen
bzw. Kinder essen, -
 die "Familien-Matrix": sie zeigt an,
wie viele Erwachsene und Kinder es in jeder der beiden Familien gibt;
die "Familien-Matrix": sie zeigt an,
wie viele Erwachsene und Kinder es in jeder der beiden Familien gibt; - die Ergebnis-Matrix
 die "Familien-Verteilungs-Matrix":
sie zeigt an, wie viele Fischstäbchen und
Kartoffeln in jeder der beiden
Familien gegessen werden.
die "Familien-Verteilungs-Matrix":
sie zeigt an, wie viele Fischstäbchen und
Kartoffeln in jeder der beiden
Familien gegessen werden.
Insgesamt haben wir also
- aus der Verteilungs-
- und der Familien-
- die Familien-Verteilungs-Matrix
gemacht.
Nehmen wir nun mal an, beide Familien
wollten zusammen essen. Dann müssten wir nur noch die Vektoraddition  +
+ =
= durchführen, wobei
durchführen, wobei  die Einkaufsliste wäre.
die Einkaufsliste wäre.
Wir müssten also für beide Familien zusammen 48 Fischstäbchen und 31 Kartoffeln kaufen
(völlig verschwunden sind da hingegen die Informationen,
- wie viele Fischstäbchen bzw. Kartoffeln Erwachsene bzw. Kinder essen,
- wie viele Familien am Essen teilnehmen
[immerhin das noch war in  sichtbar],
sichtbar],
- wie viele Erwachsene und wie viele Kinder es in jeder der beiden Familien gibt.
Aber bei der Einkaufsliste
 wären ja all diese Details auch
uninteressant.).
wären ja all diese Details auch
uninteressant.).
Nachdem wir derart anhand des Anwendungsbeispiels "Familienessen"
- eine halbwegs anschauliche Vorstellung von Matrizen bekommen und
- die Matrizenmultiplikation hergeleitet haben,
schauen wir uns nun wieder die rein (inner-)mathematischen Eigenschaften von Matrizen und ihren Multiplikationen an:
- Wie schon bei einer einzigen Familie,
also bei
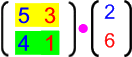 , deutlich wurde, kann eine Matrix (hier die rechte)
auch nicht-quadratisch (hier ein Vektor) sein.
, deutlich wurde, kann eine Matrix (hier die rechte)
auch nicht-quadratisch (hier ein Vektor) sein.
Noch deutlicher wird das, wenn wir uns vorstellen:
- es gibt nicht zwei, sondern drei
Essenszutaten, z.B. zusätzlich noch Salatblätter.
Dann sieht die linke Matrix z.B. so aus:

Wenn wir noch bei einer einzigen Familie bleiben, ergibt sich damit
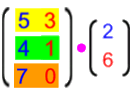 .
.
Die Ergebnismatrix gibt an, wie viel von allen (jetzt drei) Zutaten die erste Familie braucht, d.h. diese Ergebnismatrix hat jetzt automatisch die Höhe 3:
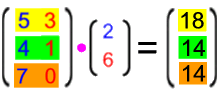
Die Ergebnismatrix hat also immer
- die Höhe der ersten und
- die Breite der zweiten Matrix:

- Nehmen wir nun des weiteren an, dass nicht eine oder zwei, sondern gleich vier Familien essen, so ergibt sich
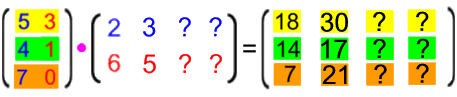
bzw.

(Spätestens hier wird man anhand der Fragezeichen bemerken, dass mich konkrete Zahlen wenig interessieren und ich zum schnöden Rechnen eh zu faul bin. Viel lieber verschwende ich meine Zeit auf die Veranschaulichung des Prinzips.)
- erfüllen die Matrizen halbwegs die oben geforderten Minimaleigenschaften für eine multiplikative "Gruppe":
- wir hatten es ja so gewollt: die Multiplikation zweier Matrizen ergibt wieder eine Matrix;
(Wie oben gesagt, müssten die Vektoren als
Teilmenge der Matrizen ebenfalls eine multiplikative "Gruppe" bilden. Aber bei der
s-Multiplikation ergibt die Rechnung "Vektor •
Vektor" doch keinen Vektor, sondern nur einen
Skalar, also eine Zahl!?
Aber Skalare bzw. Zahlen sind auch nur
[eindimensionale] Spezialfälle von Vektoren bzw. Matrizen:
ein Skalar bzw. eine Zahl ist ein 1x1-Vektor
bzw. eine 1x1-Matrix.
Also gilt doch "Vektor •
Vektor = Vektor".)
- Die Matrizenmultiplikation besitzt tatsächlich ein "neutrales Element", durch das nichts verändert wird, und zwar jene quadratische "Einheits-" oder "Identitätsmatrix",
- deren Hauptdiagonale von links oben nach rechts unten nur aus Einsen besteht, während
- alle anderen Elemente Null sind:

Das sei hier nur knapp behauptet - und man probiere es einfach mal aus.
- Die Matrizenmultiplikation ist in der Tat assoziativ, d.h. es gilt
M1 • ( M2 • M3 ) = ( M1 • M2 ) • M3
Auch das sei hier wieder nur knapp behauptet.
- Aber die Matrizen bilden
bzgl. der Multiplikation eben -
wie oben bereits angedeutet - nur halbwegs eine Gruppe: nicht
zu allen, sondern nur zu einigen quadratischen
Matrizen M1 gibt es eine
"inverse" Matrix M2 , so
das M1 •
M2 die Einheitsmatrix
 ergibt
ergibt
(was wieder nur behauptet sei; den Nachweis spare ich mir, da es solch eine inverse Matrix ja nicht immer gibt).
Wir hatten oben "Gruppen" als Schrumpfstrukturen bezeichnet. Wenn nun Matrizen bzgl. der Multiplikation nicht mal eine "Gruppe" bilden, so kann bei ihnen wohl nur von einer Schrumpf 2 -Struktur gesprochen werden:

(Schrumpfkopf)
- Bei "Gruppen" war nicht mal die Kommutativität gefordert worden, und in der Tat ist die Matrizenmultiplikation in der Regel nicht kommutativ. Z.B. ist
-

-

- und deshalb
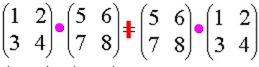 .
.
Die Matrizenmultiplikation kann aber schon allein aus einem ganz einfachen Grund nicht kommutativ sein. Erinnern wir uns dazu an das Beispiel
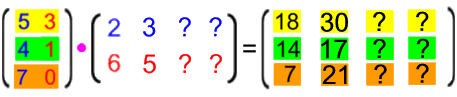
oben für vier Familien bei drei Essenszutaten. Die umgekehrte Multiplikation
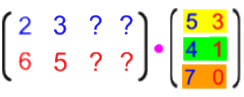
ergibt keineswegs (nur) ein anderes Ergebnis, sondern sie ist (sogar) schlichtweg unmöglich, weil die zweite Matrix nicht so hoch wie die erste breit ist.
Wenn auch die Vektoraddition ein Spezialfall der Matrizenaddition sein soll, liegt folgende Definition der Matrizenaddition nahe:

Oder:
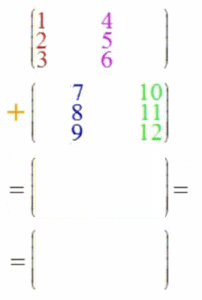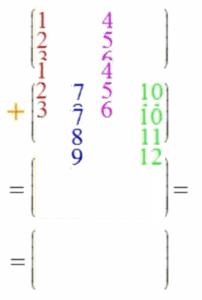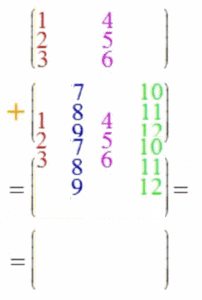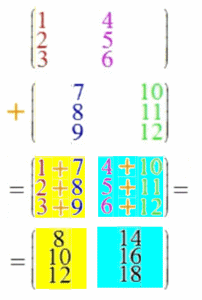
Oder:
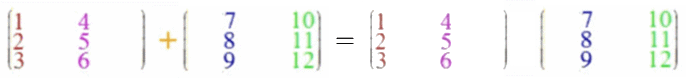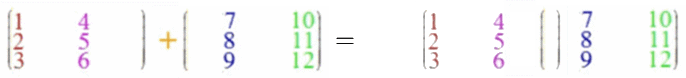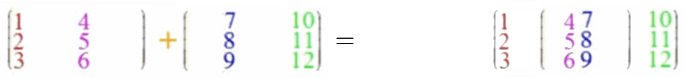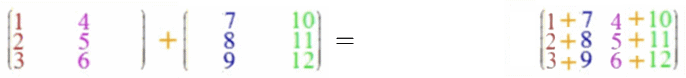
Und diese Matrizenaddition ist - im Gegensatz zur Matrizenmultiplikation - kommutativ
(weil
die Matritzenaddition sich
nämlich direkt aus der Zahl-/Skalaraddition
ergibt und die Additionen einfacher
Zahlen/Skalare in der Matrix  kommutativ sind)!
kommutativ sind)!
Bei der Matrizenaddition müssen die beiden Matrizen exakt dieselbe Form
(dieselbe Höhe [hier beidemal 3] und dieselbe Breite [hier beidemal 2])
haben, aber die Höhe der zweiten (hier 3) muss nicht
(wie bei der Matrizenmultiplikation)
gleich der Breite der ersten (hier 2) sein.
*

(Westfälische Nachrichten, 5.3.10)#
*

*

*
*
*

*

*

*
![]()
*

*

*
. 

*
*

*

*

*

*

*

*

*

*
*

*

*
*

*

*
| PS: |  |
| PPS: |
|