gigantische Mini-Probleme
klein, aber oho!
Kleinvieh macht auch Mist.
Viele SchülerInnen scheitern immer wieder an denselben Problemen
(und schreiben oftmals schlechte Klassenarbeiten nicht etwa, weil sie den neuen Stoff nicht verstanden haben, sondern - was die Lehrkraft bei der Schnellkorrektur kaum bemerkt - die ewig alten [Rechen-]Probleme mit sich schleppen),
und erfahrene LehrerInnen kennen diese Standardproblem und Fehler in- und auswendig
(so dass sie ihnen oftmals sehr gut vorbeugen könn[t]en).
Man kann sich streiten, ob die typischen Standardprobleme eine "selbsterfüllende Prophezeiung" sind:
-
indem gewisse Rechentechniken so besonders (über-?)betont werden,
-
scheitern natürlich auch viele SchülerInnen daran.
Eine denkbare (und mir dennoch ziemlich unausgegoren erscheinende) Konsequenz daraus könnte in der Tat darin bestehen, die SchülerInnen von Standardrechnungen zu entlasten, indem man diese Computern überlässt:
wieso überhaupt noch die Bruchrechnung beibringen, wo doch heute jeder Billig-Taschenrechner sie beherrscht???
Oben hatte ich gesagt, dass erfahrene LehrerInnen den Standardfehlern "vorbeugen könn[t]en". Das kleine "t" darin macht das zum Irrealis, unterstellt also, dass viele LehrerInnen (ich auch?) es eben nicht tun.
Mir scheint fast: viele erfahrene LehrerInnen
-
kennen zwar viele Standardfehler,
-
zeigen aber nicht, wie man sie los wird,
-
sondern machen in ihrer Not einfach nur vor, wie's richtig geht
(was vielen SchülerInneN zum einen Ohr rein, zum anderen raus geht: bei der nächstbesten Gelegenheit machen sie's prompt wieder falsch).
"in ihrer Not":
-
bei den allzu großen Klassen haben LehrerInnen kaum Zeit, auf individuelle Fehler einzugehen und Ursachenforschung zu betreiben;
-
oftmals bemerken LehrerInnen aber auch gar nicht, warum ein Fehler unterlaufen ist
(was die "guten" Gründe dafür waren; vgl.  "vom Richtigen im Falschen" ),
"vom Richtigen im Falschen" ),
sondern sehen nur, dass er unterlaufen ist. Sie können sich gar nicht vorstellen, wie "man" solch einen Fehler machen kann ("ich mache ihn doch auch nicht") und haben deshalb auch kein "Therapiemittel" gegen diesen Fehler.
Ein schönes Musterbeispiel für Standardfehler ist folgende Gleichungsumformung
(vgl.  ):
):
x2 - 6x + 8 = 0 | 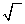

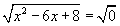

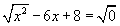
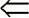
 x - 6x + 8 = 0
x - 6x + 8 = 0
 -5x + 8 = 0
-5x + 8 = 0
Da ist so mir nichts, dir nichts aus einer quadratischen Gleichung eine lineare geworden
(womit der Schüler ganz nebenbei eine Standardaufgabe durchaus - in seinem Sinne - richtig gelöst hat: "vereinfache!").
Der Fehler lag natürlich (?) bei 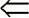 : der Schüler hat übersehen, dass man nicht aus einzelnen Summanden (x2), sondern nur aus ganzen Seiten (x2 - 6x + 8) Wurzeln ziehen darf.
: der Schüler hat übersehen, dass man nicht aus einzelnen Summanden (x2), sondern nur aus ganzen Seiten (x2 - 6x + 8) Wurzeln ziehen darf.
Da zeigt sich aber an einem neuen Problem (Wurzelziehen) ein uraltes, nämlich dass "Gleichungs(äquivalenz)umformung" immer (also nicht erst beim Wurzelziehen) bedeutet:
| dasselbe mit beiden ganzen Seiten der Gleichung tun |
Genau das ist ja ein Grundproblem des gängigen Mathematikunterrichts: viele SchülerInnen sehen überhaupt nicht die durchgehende Kontinuität (weiterhin benutzte Methoden; den Wald), sondern nur das gerade anstehende neue Problem (die Bäume) und rechnen dann, als hätte es niemals Vorarbeiten gegeben.
An diesem einzigen Beispiel sei mal gefragt, wie man solchen Standardfehlern besser vorbeugen kann.
Mir scheint, eine Möglichkeit, solch einen Standardfehler wenn auch nicht völlig auszumerzen (das wäre utopisch), so doch zu reduzieren, besteht darin,
Grundverfahren (wie eben z.B. Gleichungsumformungen) sehr viel mehr wortwörtlich zu tun (wobei ich unter "tun" mehr als nur - auch wichtig! - systematisches rechnerisches Üben verstehe). |
Zwei Tätigkeitsvorschläge:
- Gleichungen werden wortwörtlich als Waagen eingeführt, bei denen (egal, was man tut) beide Seiten immer im Gleichgewicht bleiben müssen
(vgl. mein Programm "Gleichungswaage" in der Programmsammlung  :
:
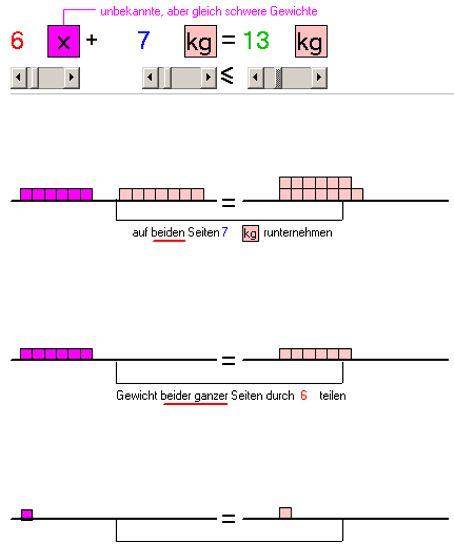
Richtiges Wiegen ist aber allemal besser als jedes Simulationsprogramm!)
Kultusministerielle Kommissionen ebenso wie viele Mathematik-Fachkonferenzen machen so viel Blödsinn, dass sie auch mal was Sinnvolles tun, sich nämlich der "gigantischen Miniprobleme" annehmen könnten. Wie beispielsweise könnte man durch höhere Anschaulichkeit Standardfehler vermeiden bei
- den simpelsten (?) Rechengesetzen,
- Term- und Gleichungsumformungen,
- der Bruchrechnung,
 ,
,- der Wurzelrechnung
- ... ???
Aber das hieße ja, von den Formalia und Vorschriften sowie den Patentrezepten (der Dreifaltigkeit aus Computer, Selbstlernen und "Anwendungsaufgaben") Abschied nehmen und - Gott bewahre! - mal kleinklein inhaltlich und konkret werden zu müssen.
Aber ich will nicht (nur) anderen die Probleme aufbürden, die ich selbst abarbeiten könnte. Die o.g. Miniprobleme genauer zu behandlen, bleibt also eins meiner Vorhaben - wenn ich mal Zeit haben sollte.
"vom Richtigen im Falschen" ),
