(und nicht etwa, wie in
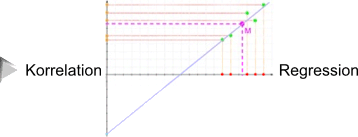 , für zwei Merkmale, nämlich die Körpergröße und zusätzlich das Gewicht)
, für zwei Merkmale, nämlich die Körpergröße und zusätzlich das Gewicht)
Mittel-/Erwartungswert,
Varianz
und Standardabweichung
Auf die Dauer möchte man nicht mehr alle Einzelwerte einer Verteilung betrachten
(und das können massenhaft sein),
sondern anhand von nur noch zwei Merkmalen
(nämlich
einen schnellen Überblick über eine Verteilung bekommen und zudem anhand dieser beiden Merkmale verschiedene Verteilung umgehend miteinander vergleichen können.
A. der Mittelwert in der Statistik
Da wir vorerst in der Statistik bleiben, ist der "Zentralwert" solange der Mittelwert
(auch "arithmetisches Mittel" genannt).
Angenommen also mal, wir messen die Körpergrößen von fünf Personen
(wobei direkt angemerkt sei, dass diese nichts mit Zufall zu tun haben, sondern fest vorgegeben sind):
| Person: | 1 | 2 | 3 | 4 | 5 | |
| erste und einzige Dimension: Körpergröße | 1,40 m | 1,50 m | 1,70 m | 1,80 m | 1,90 m |
Dabei bedeutet "erste und einzige Dimension" bzw. "eindimensional", dass wir uns bei jeder Person nur für ein einziges Merkmal, nämlich eben die Körpergröße, interessieren
(und nicht etwa, wie in
 , für zwei Merkmale, nämlich die Körpergröße und zusätzlich das Gewicht)
, für zwei Merkmale, nämlich die Körpergröße und zusätzlich das Gewicht)
"eindimensional" bedeutet auch, dass wir alle Körpergrößen auf einer Achse, nämlich der x-Achse, darstellen können:

Als Mittelwert x der Körpergrößen ergibt sich
x
= ![]() =
1,66
=
1,66
bzw. 1,66 m:

(Nebenbei: angenommen, die Körpergröße 1,40 m kommt dreimal bzw. mit der absoluten Häufigkeit 3 vor:
|
Dann lässt sich die Mittelwertberechnung natürlich folgendermaßen abkürzen:
x
= ![]() =
=
= ![]() = 1,58 )
= 1,58 )
B. der Erwartungswert in der Wahrscheinlichkeitsrechnung
Kommen wir nun zu Zufallsexperimenten, also der Wahrscheinlichkeitsrechnung. Hier sind die Einzelereignisse noch nicht (sicher) eingetreten, sondern treten nur mit jeweils einer gewissen Wahrscheinlichkeit auf. Deshalb werden zur Berechnung des "Erwartungswertes" die Einzelwerte mit ihrer jeweiligen Wahrscheinlichkeit gewichtet bzw. multipliziert. Ansonsten erfolgt aber die Berechnung genauso wie oben beim Mittelwert.
Ein Beispiel: gesucht ist die Wahrscheinlichkeit, mit der die möglichen Summen 2 bis 12 zweier Würfelwürfe auftreten:
| Summe | Würfelfolgen | einzelne Wahrscheinlichkeiten | Anzahl der Möglichkeiten | |
| 2 | 1+1 | 1/36 | 1 | |
| 3 | 1+2 | 1/36 | 2 | |
| 2+1 | 1/36 | |||
| 4 | 1+3 | 1/36 | 3 | |
| 3+1 | 1/36 | |||
| 2+2 | 1/36 | |||
| 5 | 1+4 | 1/36 | 4 | |
| 4+1 | 1/36 | |||
| 2+3 | 1/36 | |||
| 3+2 | 1/36 | |||
| 6 | 1+5 | 1/36 | 5 | |
| 5+1 | 1/36 | |||
| 4+2 | 1/36 | |||
| 2+4 | 1/36 | |||
| 3+3 | 1/36 | |||
| 7 | ||||
| 1+6 | 1/36 | 6 | ||
| 6+1 | 1/36 | |||
| 2+5 | 1/36 | |||
| 5+2 | 1/36 | |||
| 4+3 | 1/36 | |||
| 3+4 | 1/36 | |||
| 8 | 2+6 | 1/36 | 5 | |
| 6+2 | 1/36 | |||
| 3+5 | 1/36 | |||
| 5+3 | 1/36 | |||
| 4+4 | 1/36 | |||
| 9 | 4+5 | 1/36 | 4 | |
| 5+4 | 1/36 | |||
| 3+6 | 1/36 | |||
| 6+3 | 1/36 | |||
| 10 | 6+4 | 1/36 | 3 | |
| 4+6 | 1/36 | |||
| 5+5 | 1/36 | |||
| 11 | 5+6 | 1/36 | 2 | |
| 6+5 | 1/36 | |||
| 12 | 6+6 | 1/36 | 1 |
Damit ergibt sich - erst sehr umständlich - der Erwartungswert μ (gesprochen "mü")
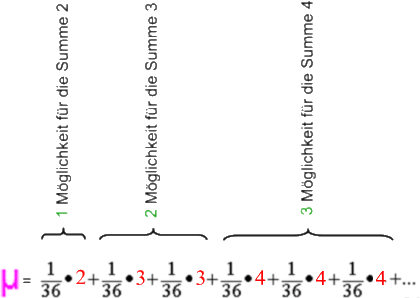
(Spätestens hier wird deutlich, dass die Berechnung des Erwartungswertes wie auch des Mittelwertes und noch mehr unten der Varianz
so dass
Da nun aber bei dem Würfelexperiment die einzelnen Summen teilweise mehrfach vorkommen, lässt sich die Berechnung des Erwartungswertes hier schon vereinfachen zu
![]()
=
![]() =
=
=
![]() • ( 2 + 6 + 12 + 20 + 30 + 42 + 40 + 36 + 30 + 22 + 12 ) =
• ( 2 + 6 + 12 + 20 + 30 + 42 + 40 + 36 + 30 + 22 + 12 ) =
=
![]() • 252 =
• 252 =
= 7
Man kann also auch sagen: im Schnitt werden wir (= Futur) die Würfelsumme 7 würfeln:
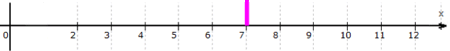
Das einfache Ergebnis μ = 7 dürfte uns
(zumindest im Nachhinein)
nicht sonderlich erstaunen, da ja die Verteilung symmetrisch um die 7 angeordnet war:
| Summe | Anzahl der Möglichkeiten | |
| 2 | 1 | |
| 3 | 2 | |
| 4 | 3 | |
| 5 | 4 | |
| 6 | 5 | |
| 7 | 6 | |
| 8 | 5 | |
| 4 | 4 | |
| 10 | 3 | |
| 11 | 2 | |
| 12 | 1 |

Die Varianz ist ein Maß für die durchschnittliche Abweichung der verschiedenen Verteilungswerte vom Mittel- bzw. Erwartungswert.
Kehren wir zu unserem obigen Beispiel der Körpergrößen zurück.
Ein mögliches Maß für die Abweichung der Verteilungswerte vom Mittelwert wäre der Abstand der Werte 1,40 m, 1,50 m, 1,70 m, 1,80 m und 1,90 m vom Mittelwert 1,66 m.
Man könnte also auf die Idee kommen, den
Mittelwert der Abstände vom Mittelwert
folgendermaßen zu rechnen:
Dabei ergeben sich allerdings
die sich gegenseitig aufheben:
![]() =
=
=
![]() =
=
= 0
Um diesen Fehler zu beheben, erinnern wir uns daran, dass Abstände ja immer positiv gemessen werden, was wir durch Absolutstriche erreichen können:
![]() =
=
=
![]() = 0,168
= 0,168
Wenn man nun einen Bereich um x = 1,66 mit 0,168 nach links und 0,168 nach rechts legen würde, würde man Folgendes erhalten:

Die beiden knappen Merkmale "Mittelwert" und "Bereich" gäben dann schon einen ziemlich guten Überblick über die Gesamtverteilung.
Ein anderer Weg, nur mit positiven Zahlen zu rechnen, ist das Quadrieren. Natürlich verzerrt es die Werte
(- eine Abweichung von 1 bleibt durch
Quadrieren eine 1,
- eine Abweichung von 2 wird durch Quadrieren
doppelt so groß, nämlich 4,
- ...),
aber genau diese Verzerrung hat auch Vorteile: große Abweichungen werden durch Quadrieren noch sehr viel größer, d.h. das Quadrieren betont vor allem Ausreißer ganz weit links oder rechts vom Mittelwert.
Manchmal ist genau das gewollt, manchmal aber auch irreführend.
(Beispiel: Bill Gates betritt eine new yorker Kneipe, in der vorher nur arme Schlucker pichelten:
Will man das - oder hält man solch einen Gedankengang für absurd, weil sich realiter nichts am Einkommen der armen Schlucker ändert?
Nebenbei: den Trick des Quadrierens hat kein Geringerer als "der Fürst der Mathematik"
mit seiner
![]() "Methode der kleinsten Quadrate" erfunden.)
"Methode der kleinsten Quadrate" erfunden.)
Mit dem Trick des Quadrierens wird nun die (hier: empirische) Varianz Vx definiert, und in unserem Körpergrößenbeispiel ergibt sich:
Vx =
![]() =
=
= ![]() =
=
![]() =
=
= ![]() =
0,0344.
=
0,0344.
Nun wollen die MathematikerInnen das dreiste vorherige Quadrieren aber doch ein wenig rückgängig machen, ziehen deshalb am Ende aus der Varianz wieder die Wurzel und erhalten damit die (hier: empirische) Standardabweichung sx:
sx =
![]() .
.
Damit ergibt sich dann folgender Bereich um den Mittelwert:

Es lässt sich nun sagen, dass die Körpergrößen "im Schnitt" im Standardabweichungsbereich um den Mittelwert liegen.
("ein wenig rückgängig machen" ist allerdings ein Euphemismus für eine besonders brutale [falsche] Art des Wurzelziehens:
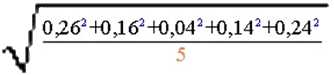 ≠
≠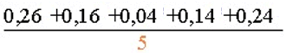 .
.
Und noch eine kleine Anmerkung: bei der obigen Verteilung
|
in der der Wert 1,40 m dreimal vorkommt und die laut obiger Rechnung den Mittelwert 1,58 m hat, lässt sich die Varianzberechnung ebenfalls abkürzen:
![]() =
=
=
![]() = ... )
= ... )
B. (theoretische) Varianz und Standardabweichung
in der Wahrscheinlichkeitsrechnung
Kehren wir wieder zu dem obigen Beispiel der Summe zweier Würfelwürfe zurück, bei der, wie wir berechnet haben, der Erwartungswert μ = 7 ist.
Auch hier berechnen wir die quadratischen Abweichungen der möglichen Summen 2 bis 12. vom Erwartungswert, nur dass diese Abweichungen wieder mit ihren jeweiligen Wahrscheinlichkeiten gewichtet, d.h. mit ihnen multipliziert werden. Die (theoretische) Varianz σ2
(wobei
σ"Sigma" ausgesprochen wird:
 )
)
wird dann berechnet als
σ2=
![]() +
+
+ ![]() =
=
= ![]() =
=
=
![]() =
=
=
![]() =
=
=
![]() =
5,83
=
5,83
Daraus ergibt sich die (theoretische) Standardabweichung σ als
σ =![]() ≈ 2,41
≈ 2,41
und somit der Bereich, in dem die Würfelsummen "im Schnitt" liegen werden, als
