die radikale mathematische Konsequenz aus dem Nichtwissen

"Ich weiß, DASS ich nichts weiß."
(Sokrates)

Oder muss es korrekt doch heißen?:
"Ich weiß, WAS ich nicht weiß."
(vgl. )

• Mathematiker sind vornehme Agnostiker, also solche, die die Existenz Gottes weder voraussetzen

(und den Glauben daran rabiat bei anderen einfordern)

noch

(wie viele Stumpfatheisten heutzutage)

lautstark leugnen, sondern mit Ludwig Wittgensteins berühmtem und ach so oft missverstandenem Bonmot denken:

"[...] wovon man nicht sprechen kann, darüber muss man schweigen."

• Aber von dieser Position aus konstruieren sie sich dann eben doch einen "Gott" zurecht

(so etwa im Sinne von Ludwig Feuerbach)

und lassen es dann offen, ob dieses Konstrukt mit einem realen Gott übereinstimmt.

1. Beispiel:

Ob ein Würfel tatsächlich "laplace-verteilt" bzw. "fair" ist, also alle Seiten mit derselben Wahrscheinlichkeit fallen, oder ob er "gezinkt" ist, also eine Seite häufiger auftritt, lässt sich überhaupt nicht vorher (a priori) sagen.

Zwar sehen die heutzutage industriell gefertigten Würfel absolut symmetrisch und perfekt aus, aber sogar sie werden klitzekleine (allerdings nicht beabsichtigte) Unregelmäßigkeiten haben, nämlich z.B.  dadurch, dass auf der 6er-Seite mehr Vertiefungen sind als auf der gegenüberliegenden 1er-Seite, solch ein Würfel also auf der 6er-Seite leichter ist.

Normalerweise interessieren uns solch minimale Abweichungen beim Spielen allerdings nicht, aber uns geht's hier ja (wie immer in der Mathematik) "ums Prinzip". Und überhaupt finde ich offensichtlich laplace-verteilte Würfel sterbenslangweilig

(vgl. und
)

• bei denen man wegen unregelmäßiger oder ungewöhnlicher Form auf Anhieb nicht weiß, ob sie laplace-verteilt sind oder nicht, die man also erstmal ausprobieren muss;
• die offensichtlich nicht laplace-verteilten "Würfel" , bei denen man die Wahrscheinlichkeit jeder Seite also überhaupt erst herausfinden muss

(nebenbei ist es allemal interessant, zu solchen unregelmäßigen "Würfeln" spezielle Spiele zu erfinden, bei denen eine weniger wahrscheinliche Seite höhere Gewinne erzielt, wozu man allerdings erst mal durch Ausprobieren herausfinden muss, wie groß die jeweiligen Seitenwahrscheinlichkeiten sind;
und interessant ist es auch, von der geometrischen Form auf die Wahrscheinlichkeiten zu schließen: fällt z.B. eine doppelt so große Seite auch doppelt so oft?)

In allen drei Fällen ist also die Wahrscheinlichkeit der Seiten nicht von Anfang an klar

(bzw. im ersten Fall meint man vorher nur fälschlich, es läge eine Laplace-Verteilung vor),

und muss man deshalb die Würfel (vielfach) ausprobieren, kann also erst nach dem Ausprobieren (a posteriori) sagen, welche Wahrscheinlichkeiten vorliegen.

Mathematiker ziehen daraus einen radikalen Schluss:

• es mag "die" (bereits vorher in Würfeln angelegten) Wahrscheinlichkeiten zwar geben (oder gar: es gibt sie tatsächlich!),
• aber da wir sie grundsätzlich (!) nicht (vorher) erkennen können, tun die Mathematiker so,
  • als gäbe es diese a-priori-Wahrscheinlichkeiten gar nicht,
  • bzw. sie argumentieren zumindest nicht damit.
  • Sondern für sie gibt es nur die realen (nicht mehr wahrscheinlichen) Ergebnisse vielfachen Würfelns, aus denen sie die relativen Häufigkeiten berechnen

(z.B.: die 6 ist in 3 von 10 Würfen gefallen, also ist ihre relative Häufigkeit ³/₁₀), 

(sie sagen also, die Wahrscheinlichkeit [!] für die 6 ist ³/₁₀ ).

Bleiben wir kurz bei dem Ergebnis ³/₁₀ :

1. solle man offensichtlich immer dabei sagen, wie oft man gewürfelt hat

(die Feststellung einer Wahrscheinlichkeit nach wenigen Würfen ist auch wenig verlässlich, während immer mehr Würfe auch höhere Verlässlichkeit erzeugen; vgl. unten das "Gesetz der großen Zahlen"), 

1. kann das Ergebnis nun zweierlei bedeuten:

1. dass die Wahrscheinlichkeit für 6 tatsächlich ³/₁₀ und nicht ¹/₆ ist, dass der Würfel also gezinkt ist,
2. dass das Ergebnis ³/₁₀ nach nur zehn Würfen noch sehr ungenau ist, dass also der Würfel fälschlicherweise als gezinkt eingeschätzt wird, in Wirklichkeit aber doch laplace-verteilt ist.

In beiden Fällen aber beißt sich die Katze scheinbar in den eigenen Schwanz, denn wir messen da das Endergebnis ³/₁₀ (die Wahrscheinlichkeit nach zehn Würfen) ja eben doch an einer im Würfel enthaltenen a-priori-Wahrscheinlichkeit: der Würfel war

• im Fall A. von Anfang an gezinkt
• im Fall B. von Anfang an laplace-verteilt,

und wir haben nur nachträglich

• im Fall A. das Gezinkt-Sein bestätigt,
• im Fall B. die Laplace-Verteilung fälschlich nicht erkannt.

"scheinbar", da wir

• ja noch immer nicht wissen (und letztlich auch nie wissen werden), ob der Fall A. oder aber der Fall B. vorliegt,
• und wir A. und B. sowieso vorsichtiger formulieren sollten:

1. , ... dass der Würfel also gezinkt zu sein scheint bzw. sein könnte,
2. , dass das Ergebnis ³/₁₀ nach nur zehn Würfen vermutlich noch sehr ungenau ist, dass also der Würfel fälschlich als gezinkt eingeschätzt werden, in Wirklichkeit aber doch laplace-verteilt sein könnte.

Meinem Verständnis nach besagt das "Gesetz der großen Zahlen"

(vgl. )

nämlich

• nicht, dass sich die relativen Häufigkeiten auf Dauer den "wahren", von Anfang an im Würfel "enthaltenen" Wahrscheinlichkeiten annähern,
• sondern es legt "nur" ein Kriterium fest, wann wir die Folgerung

  "relative Häufigkeit (nachträgliche) Wahrscheinlichkeit"

  mit "gut" oder "besser" bezeichnen: nämlich dann, wenn oft und immer öfter gewürfelt wird. Und selbst das ist wieder nur eine Wahrscheinlichkeitsaussage:

  • wenn man 1000 mal gewürfelt hat, wird man die (nachträgliche) Wahrscheinlichkeit als "gut" bezeichnen,
  • obwohl einen das ja durchaus mögliche Ergebnis, dass man 1000 mal einzig und allein Sechsen gewürfelt hat, eben doch skeptisch macht

(spätestens dann, aber vermutlich doch viel früher wird man sich den Würfel doch mal genauer anschauen und feststellen, dass er

1. entweder allseitig nur Sechsen zeigt, also schwerst gezinkt ist,
2. oder aber auch andere Seiten hat, was einen vermuten lassen wird, dass der tausendfache Sechserwurf zwar höchst unwahrscheinlich, aber doch möglich, allemal aber zweifelhaft ist).

Das "Gesetz der großen Zahlen" besagt nun aber, dass weitere (z.B. zehntausend) Würfe zunehmende Sicherheit (und letztlich doch nur eine erhöhte Wahrscheinlichkeit, richtig zu liegen) erbringen werden.

Und überhaupt beschäftigt sich ein Großteil der Statistik damit, Kriterien dafür zu entwickeln, wie verlässlich ausschnitthafte Erhebungen sind und was man aus ihnen mit welchem "Recht" schließen kann

(vgl. Varianz, Signifikanzniveaus, Hypothesentests ...).

Nach meinem Verständnis ist also das "Gesetz der großen Zahlen" weder von Gott gegeben noch eine logische mathematische Folgerung (ein "Satz"), sondern (wie alle Gesetze) menschengemacht.

(Aber man widerspreche mir, wenn mein Verständnis des "Gesetzes der großen Zahlen" mathematisch falsch sein sollte.)

Das Würfeln ähnelt also der Quantentheorie: wie ein Quantenzustand aussah, bevor wir ihn messen, ist grundsätzlich nicht feststellbar, und zwar

• nicht etwa, weil uns über den vorherigen Zustand hinreichende Kenntnisse fehlen,
• sondern weil es vorher überhaupt keine eindeutigen Zustände, sondern nur Wahrscheinlichkeiten (etwa für die Orte von Elementar-"Teilchen") gab.
• Im selben Augenblick aber, in dem wir messen, geschieht der "Wahrscheinlichkeits-Kollaps", d.h. gefrieren die unendlich vielen (wenn auch teilweise verschieden wahrscheinlichen) Möglichkeiten urplötzlich zu einer einzigen (evtl. auch höchst unwahrscheinlichen, dann aber eben doch eingetretenen) Gewissheit: wenn etwas passiert, ist es eben nicht mehr wahrscheinlich.

(... was mich ans Schockfrosten erinnert:

"Das Schockfrosten oder Schockgefrieren ist ein industrielles Verfahren für die Herstellung von Tiefkühlkost. Innerhalb sehr kurzer Zeit (meist nur Minuten [und bei Quantenzuständen in einem einzigen Augenblick]) wird die Temperatur der einzufrierenden Lebensmittel auf die gewünschte Lagertemperatur (häufig −20⁰ C und tiefer) abgesenkt."
[Quelle:   ])

(vgl. )

Der Knackpunkt ist aber eben "die Tangente in diesem Punkt zeichnen". Man kann das sehr gut nach Augenmaß machen, und "im Alltag" ist es ja auch wirklich nebensächlich, ob in

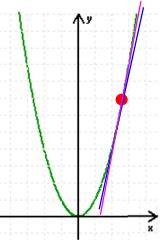
die violette oder die blaue Tangente exakter ist.

Mathematiker aber wollen (zumindest rechnerisch) natürlich die exakte Tangente haben.

Und auch hier ziehen sie wieder aus ihrem Nichtwissen, wie denn nun genau die exakte Tangente aussieht, den "einzig wahren" Schluss, dass es sie gar nicht gibt, sondern dass man sie überhaupt erst konstruieren muss.

Wie typisch in der Mathematik, machen die Mathematiker sich nun bewusst,

1. , was sie nicht können (Parabeln und überhaupt alles Krumme),
2. , was sie sehr wohl können (Steigungen von Geraden berechnen),

und versuchen dann (enorm erfolgreich!), das Unbekannte durch das Bekannte anzunähern

(vgl. ):

sie wählen nun zusätzlich zu dem Punkt, in dem die Steigung bestimmt werden soll, einen weiteren Punkt, und durch diese beiden Punkte legen sie dann eine Gerade

(die die Parabel zweifach schneidet und deshalb "Sekante" genannt wird [lat. secare = schneiden]),

deren Steigung sich bekanntermaßen leicht mit dem Steigungsdreieck bestimmen lässt:

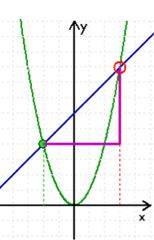
Und nun lassen sie den zweiten Punkt sich auf der Parabel in Richtung des ersten (unveränderten) Punktes laufen, und zwar derart, dass der zweite Punkt zwar  beliebig nah an den ersten Punkt herankommt, ihn aber nie erreicht

(wenn er ihn erreichen würde, gäbe es nicht mehr zwei Punkte, durch die man eine Sekante ziehen und mittels derer man dann die Steigung bestimmen könnte):

 
(vgl. )

Bei sukzessiver Annäherung des zweiten Punktes an den ersten Punkt unterscheiden diese Sekanten sich dann nur noch minimal (aber immer noch ein bisschen!). Und eben den Grenzwert dieser Sekanten (der eigentlich nie angenommen wird) nennt man "Tangente". Diese Tangente kommt also überhaupt erst durch das Sekantenverfahren zustande und ist auch gar nicht anders erhältlich, d.h. ohne das Sekantenverfahren gibt es sie gar nicht.

Und entsprechend nennt man den Grenzwert der Sekantensteigungen dann "Steigung der Parabel in unserem Punkt". 

3. Beispiel:

"Schließlich überwand sich der Junge doch und sah zur Erde. Da kam es ihm vor, als läge unter ihm ein großes Tuch ausgebreitet, das in eine unglaubliche Menge von kleinen und großen Karos eingeteilt war. Um Gottes willen, wohin bin ich nur geraten? fragte er sich. Er sah nichts weiter als ein Karo neben dem anderen. Einige waren schräg und andere länglich, doch alle waren eckig und hatten gerade Ränder, nichts war rund, und nichts war krumm. »Was ist das nur für ein großes kariertes Stück Stoff, das ich da unten sehe?« sagte der Junge vor sich hin, ohne zu erwarten, daß jemand ihm antworten würde. Doch die Wildgänse, die rechts und links von ihm flogen, riefen sogleich: »äcker und Wiesen. äcker und Wiesen.« Da wurde ihm klar, daß dieses große karierte Tuch, das er gerade überflog, der flache Boden von Schonen war. Und er begriff nun auch, weshalb es so vielfarbig und kariert aussah. [...] Als der Junge sah, wie kariert das alles war, mußte er ganz einfach lachen." (aus )

Weil Umfang und Fläche des krummen (!) Kreises sich ebenfalls nicht direkt exakt abmessen und berechnen lassen

(und dasselbe Problem taucht dann später bei der Integration auf),

sagen wir auch hier erstmal, dass es den Umfang und die Fläche eines Kreises gar nicht (vorher) gibt.

Vielmehr werden Kreisumfang und -fläche wieder durch Gerades, nämlich z.B. Dreiecke

(deren Seiten bzw. Flächen man leicht [?] berechnen kann),

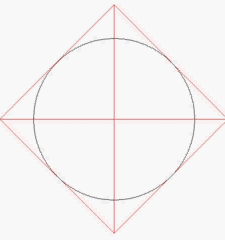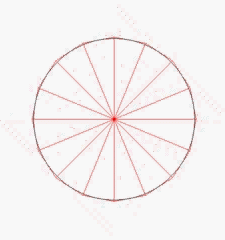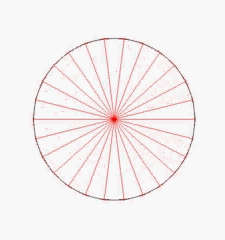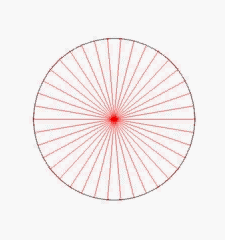
angenähert, und zwar in einem ersten Anlauf z.B. folgendermaßen:

(vgl. )

Und als Kreisumfang bzw. -fläche definiert die Länge der Außenseiten bzw. die Fläche, gegen den die Dreiecksaußenseiten bzw. Dreiecksflächen "konvergieren".

Offensichtlich bleiben aber bei dieser Art des Vorgehens der außen-Umfang bzw. die Fläche der Dreiecke immer minimal unterhalb des exakten Kreisumfangs- bzw. der exakten Kreisfläche

(zwischenzeitlich argumentieren wir hier also doch mal ganz kurz mit dem exakten, von Anfang an gegebenem Kreisumfang bzw. der exakten Kreisfläche).

Nun kann man die Dreiecksannäherung aber auch von außen, also z.B. so vornehmen:

Beide Annäherungen, also sowohl die von innen als auch die von außen, laufen gegen dieselben Werte

(obwohl sie von keiner der beiden Annäherungen jemals exakt angenommen werden!),

die wir nun erst als Kreisumfang bzw. Kreisfläche definieren, und zwar jetzt wieder völlig unabhängig davon, ob es einen von Anfang an gegebenen Kreisumfang bzw. eine von Anfang an gegebene Kreisfläche gibt.

Es sei noch erwähnt, dass wir uns mit diesen Verfahren sowohl in der Formel für den Kreisumfang als auch in der für die Kreisfläche den (glücklicherweise denselben!) Wert  π einhandeln

(vgl. ).

Dieser Wert von π ≈ 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 … ist aber irrational, d.h. weder endlich noch periodisch hinter dem Komma. In jeglicher Rechnung wird man aber nur mit endlich vielen Nachkommastellen rechnen können (was "im Alltag" ja auch allemal reicht), d.h. auch bei π  (und damit bei jeder Kreisumfangs- bzw. Kreisflächenberechnung) ist nur eine (allerdings beliebig genaue) Annäherung möglich.