oder
auch in der Mathematik halbe Sachen machen
oder
auch in der Mathematik halbe Sachen machen
vgl.
|
Drei Sätze, die ich in meiner Kindheit und Jugend oft gehört habe:
Diese drei Sätze haben ja durchaus den Vorteil, Durchhaltevermögen, Frustrationstoleranz und Ehrgeiz einzufordern und damit evtl. auch zu trainieren
(was mir im Leben sicherlich oft geholfen hat).
Der Nachteil ist aber, dass man (!) sich allzu leicht in eine Sache verrennt, und sei sie noch so frustrierend, schwachsinnig oder gar vollends aussichtslos.
(Eine mögliche Folge des Satzes "Was macht macht, macht man richtig" könnte allerdings auch sein: "da ich eh nichts richtig hinkriegen werde, fange ich erst gar nicht an.")
"Man macht keine halben Sachen" gilt
(zumindest vordergründig)
insbesondere in der Schulmathematik
(wie wohl in kaum einem anderen Fach):
es werden üblicherweise ausschließlich mathematische Sachverhalte
durchgenommen, die mit
vollständig lösbar sind
(lassen wir hier mal die höchst selten im Unterricht vorkommenden unlösbaren Gleichungen weg
[z.B. wenn eine Parabel gar keine Nullstelle hat]).
Das ausschließliche Bearbeiten vollständig lösbarer Aufgabe hat zwei Effekte:
(wenn überhaupt, dann nur alle von ihr selbst gestellten)
Probleme lösen kann, womit die Mathematik
(und mit ihr die Hohenpriester der Mathematik, also die Mathematiker)
schnell als superschlau, aber auch besserwisserisch dasteht (dastehen).
(man frage mal ein paar Monate später nach "altem" Stoff).
Sie lernen aber nie, wie man an offene Probleme rangeht - und zwar auch solche, die
Zurück zur obigen Andeutung, dass der Satz "Man macht keine halben Sachen" in der Schulmathematik nur vordergründig gilt: gerade weil andauernd nur lösbare Probleme betrachtet werden, wird vieles nur halb durchgenommen.
Ein Beispiel: in der 9. Klasse werden die Nullstellen (y = 0) von Parabeln und ihre Schnittpunkte mit der y-Achse (x = 0) wohl vor allem deshalb durchgenommen, weil für sie gerade das rechnerische Rüstzeug erarbeitet werden kann (Wurzeln, p-q-Formel ...).
Andere markante Eigenschaften von Parabeln und anderen Funktionen wie
sind in der 9. Klasse rechnerisch noch nicht erhältlich - und werden deshalb in der Regel nichtmal erwähnt.
Die Schüler erfahren in der 9. Klasse somit nur wenig über quadratische Funktionen - und den Rest erst in der Oberstufe, womit sie in der 9. Klasse blind für die Zukunft der Mathematik in der Schule bleiben
(vgl.
).
Die Schüler machen also in der 9. Klasse eine Sache (die quadratischen Funktionen) nicht ganz, sondern nur "halb".
In der Schulmathematik ist ab der Mittelstufe das alles bestimmende Kriterium die Berechenbarkeit
(während in der Unterstufe Geometrie und Algebra noch weitgehend getrennt sind und damit fast wie zwei unterschiedliche Schulfächer aussehen, die nur zufällig von demselben Lehrer unterrichtet werden).
Diese Dominanz der Berechenbarkeit bestätigt aber nur das Klischee, dass Mathematik geradezu synonym mit Rechnen ist und in diesem komplett aufgeht.
In Wirklichkeit wird damit aber nur höchstens die halbe
(!) Mathematik vermittelt. Die andere Hälfte der Mathematik
besteht hingegen aus
Die übliche Perspektive auf die Schulmathematik ist die pessimistische:
wenn das Glas
ist, ist das zu wenig.
Ich hingegen bin Optimist: wenn das Glas 
ist, ist das doch schon ziemlich viel!
Ich plädiere also dafür, in der Schulmathematik auch mal Sachen nur halb zu machen, d.h. offene und mit den jeweils derzeitigen Mitteln nicht vollständig abschließbare Projekte durchzuführen.
Dabei weiß ich genau, dass dafür bei den derzeit völlig überfrachteten Lehrplänen und der daraus folgenden totalen Reglementierung des Mathematik-Unterrichts gar keine Zeit ist. Dann müsste
(wohl ein Irrealis)
man die Lehrpläne eben massiv entschlacken und dadurch Freiräume schaffen. Aber der Gedanke der Freiheit passt ja nicht in die Köpfe der Schulpolitiker und -bürokraten.
Es ist mir bislang nicht gelungen herauszufinden, warum das Ding
"Oloid"
heißt.
Ein Oloid ist (nicht nur) für Schüler sowohl visuell faszinierend als auch haptisch: sobald man Schülern einen Oloid in die Hand gibt
(vgl.
),
(ein faszinierender Widerspruch:)
insgesamt doch gradlinige Fortbewegung:
Wenn das keine interessanten Anlässe für eine weitere Beschäftigung mit dem Oloid sind!
|
|
"Für jedes komplexe Problem gibt es immer eine
einfache Lösung. Und sie ist immer falsch." Oft gibt es in der Mathematik für schwierige Probleme einfache Lösungen - und leider für einfache Probleme schwierige Lösungen. |
Um es gleich vorweg klarzustellen: die Berechnung des Oloids liegt weit jenseits der mathematischen Fähigkeiten von Schülern
(und auch meinen),
denn die rechnerischen Gleichungen für das Oloid sehen so aus:
Parameterdarstellung der Oberfläche:
Flächeninhalt der Oberfläche:
|
(Das überaus Erstaunliche dabei ist, dass nach all den überaus komplizierten Rechnungen etwas relativ Einfaches herauskommt: die Oberfläche eines Oloids ist genauso groß wie die einer Kugel mit gleichem Radius: woher "wusste" der Oloid das, bzw. wie lässt es sich anschaulich begreifen?) |
Oberfläche des Oloids
(nicht der Flächeninhalt
dieser Oberfläche):
|
(... wobei in der Mathematik üblicherweise
nebenbei: die Oberfläche des Oloids ist nur ein Ausschnitt aus der gesamten Lösungsmenge der Gleichung O: |
(Quelle aller Rechnungen:
)
Wenn aber die Berechnung des Oloids in der Schule ausgeschlossen ist, kann man ihn eben nur "halb"
(und das heißt: nur geometrisch)
durchnehmen.
Am besten ist es natürlich, wenn der Oloid den Schülern nicht fertig vorgesetzt wird, sondern sie ihn selbst entdecken.
Das ist immerhin dann möglich, wenn man nur eine kleine Vorgabe macht, nämlich
.
Hier könnte man wahrhaft offen anfangen, nämlich die Schüler einfach verschiedene Gebilde zusammenstecken lassen.
Eine schnelle Internetrecherche ergibt, dass dabei meist symmetrische oder anderweitig regelmäßige Gebilde entstehen:
(Dabei sind durchaus gleichzeitig komplexe und doch besonders gleichmäßige und damit schöne Gebilde möglich:
.)
Bevor wir aber genauer auf solche Regelmäßigkeiten eingehen: wenn man das Steckspiel "ernst" nimmt, statt es nur als Mittel zum Zweck "Oloid" zu betrachten, gilt es erstmal zu verstehen, wie die Form des
Einzelkreises
die zusammwngeswtzten Gebilde ermöglicht bzw. einschränkt:
,
so dass zwei benachbarte Schlitze einen Winkel von 360° : 16 = 22,5° bilden
(das hört sich arg "schief" an, hat aber immerhin zur Folge, dass 4 • 22,5° = 90°, womit im Folgenden auch rechte Winkel möglich sind;
in Wahrheit war es aber wohl umgekehrt: die Konstrukteure des Spiel wollten rechte Winkel ermöglichen und haben diese dann in vier Teile zu je 22,5° unterteilt);
...
(Nebenbei: es gibt auch kleinere Versionen des Spiel mit nur acht Schlitzen
,
so dass nur Winkel von 360° : 8 = 45° und Vielfache davon möglich sind.)
Natürlich habe ich nach wie vor das Oloid im Hinterkopf, und daher stellt sich nun die Frage, wie man die Schüler zu diesem hingeleiten kann, ohne sie (allzu sehr) zu gängeln. Eine Möglichkeit scheint mir darin zu liegen, die von den Schülern hergestellten Gebilde zu sortieren bzw. zu klassifizieren. Dabei müsste eigentlich als ein wichtiges Kriterium die oben schon erwähnte Symmetrie bzw. Regelmäßigkeit herauskommen - und da liegt nun die Frage nach dem einfachsten regelmäßigen Gebilde nahe.
Das einfachste regelmäßige Gebilde besteht aber aus nur zwei Einzelkreisen, und die einzig mögliche Steckkombination ist da
.
Dieses Gebilde gilt es nun genauer zu verstehen. Dabei meine ich mit "Verstehen" noch keineswegs einen im eigentlichen Sinne mathematischen (geometrischen), sondern man lasse die Schüler einfach mit diesem einfachen Gebilde rumspielen. Dabei müsste ihnen eigentlich die oben schon erwähnte seltsam torkelnde und dennoch geradlinige Bewegung auffallen, mit der das Gebilde über den Tisch rollt - und damit hätten die Schüler hoffentlich "Blut geleckt"!
Wenn erstmal solches Interesse geweckt wäre, könnte man "mathematischer" (geometrischer) werden und untersuchen, wie das Gebilde aufgebaut ist:
Hier wird nun interessant, dass in der größeren Spielversion zwei Schlitzsorten vorkommen, nämlich eine längere und eine kürzere:
Da liegt es nahe
(aber diesen Tipp muss wohl der Lehrer geben),
bei zwei Einzelkreisen je einen der längeren Schlitze noch weiter
zum Kreismittelpunkt hin zu verlängern, und zwar so, dass
(Nebenbei: hier nun wird der obige Satz
"die Oberfläche eines Oloids ist genauso groß wie die einer Kugel mit gleichem Radius"
endlich verständlich:
)
Nun wäre es sinnvoll, das Oloidskelett noch weiter zu erkunden. Dazu könnte man drei Fragen stellen, die durch die Schüler mittels eigener Experimente beantwortet werden sollten:
;
daraus folgend:
(Modell aus zwei alten Fahrradfelgen)
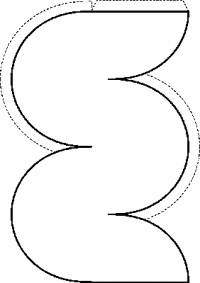
Ein alternativer Zugang könnte so aussehen,
und wird gebeten, daraus
(ohne Schneiden und Knicken)
einen 3D-Körper zu erstellen, wobei die Hülle des Oloids entsteht.
Wenn dann die beiden Gruppen in einem Klassenraum zusammen kommen, könnte man die Ergebnisse vergleichen:
ergibt die 2D-Abrollspur ,
ergibt umgekehr eine 3D-Oloid-Hülle
.Da stellt sich dann vielleicht doch die Frage, wie man aus dem Oloidskelett ein vollständiges Oloid machen könne.
Und da würde ich nun mit allen Schülern zusammen
(also nicht mehr in den zwei vorher getrennten Gruppen)
folgendermaßen vorgehen:
Jeweils zwei, damit jeder Schüler
(Wenn das Oloidsklett erstmal entdeckt ist, gibt es eine sehr einfache Methode, mit den Schülern relativ große und gut rollende Oloidskelette herzustellen, nämlich aus zwei alten CDs:
)
Diese Weiterarbeit besteht nun in
(Vorsicht, die Schüler werden dabei ausgerechnet im klinisch reinsten Fach, nämlich der Mathematik, eventuell endlich mal richtig schön schmutzig:
):
heraus kommt dabei bei ensprechender Sorgfalt etwas wirklich Schönes und "Handschmeichlerisches".
(Dabei ist es sehr wichtig ist, dass die Schüler das selbst hergestellte Oloid, auf das sie hoffentlich stolz sind, behalten und mit nach Hause nehmen dürfen.
Es wäre nebenbei vermutlich eine Weltneuheit, wenn Schüler aus dem Mathematikunterricht endlich mal etwas Be-Greifbares mit nach Hause brächten und vielleicht sogar freiwillig in ihr Regal stellen würden.)
Denkbar wäre auch noch eine Verschönerung der Oloid-Oberfläche durch Polieren und farbiges Lackieren.
Eine Ergänzung besteht darin, dass die Schüler anhand eines größeren Oloids
(also nicht bloß Oloidskeletts)
untersuchen, welche Punkte beim Abrollen jeweils den Tisch berühren, und dadurch die "Streckenform"
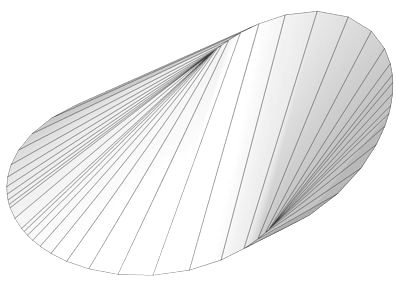
entdecken, die das gleichmäßige Abrollen des Oloids vielleicht überhaupt erst verständlich macht.
Mit der "Streckenform" lässt sich wiederum ein schönes Fahrradfelgen-Modell bauen:
Erst nachdem das Oloid derart vielfach selbst erfahren und hergestellt wurde, würde ich die Schüler zu einer weitergehenden Oloid-Recherche aufs Internet loslassen.
Und da finden sie dann z.B.
Hintergründe
über den Erfinder/Entdecker des Oloids, also
Paul Schatz:: 
,
einen Eindruck von der höchst schwierigen Mathematik des an
sich doch sehr einfachen Oloids,
(eine Vielzahl schöner Oloide sowie
"Oloid-Zubehör" gibt es bei
zu kaufen)
Diese Geräte werden vor allem zum Umrühren von Flüssigkeiten eingesetzt
,
aber auch als Schiffsantrieb:
(hergestellt von Auszubildenden der Firma thyssenkrupp)
Eine Oloidskelett-Version:
Ein schöner Tipp zur Funktionsweise des Oloid-Motors ist nebenbei die abgenagte Oloid-Skelett-Version:
(Animation nach )
(Warum eigentlich nicht mal einen Oloid-Rührer mit Schülern bauen?)
Bemerkenswert sind auch noch andere Oloid-Formen, die genauso abrollen wie der Standard-Oloid:
(was nebenbei eine schöne Minimalfläche ist)
Von diesen anderen Oloid(?)formen scheint mir insbesondere der letzte interessant: er ist in sich verdrehbar
,
so dass man auch einen klassischen Kreisel herstellen kann:
Dieses Verdrehen scheint mir die typische Senkrecht-Konstruktion
des Oloids nochmal besonders
gut zu illustrieren oder sogar überhaupt erst erkennbar zu machen.
Ein interessante Frage ist aber, weshalb die "anderen"
Oloiden genauso funktionieren wie das Standard-Oloid
. Mit den Vorarbeiten oben kann man darauf
antworten: alle Oloidformen
haben ,hinausragen, aber durchaus ausgehölt
sein.Nachdem der Oloid derart erarbeitet ist, könnte man noch einem Hinweis auf dem oben bereits gezeigten Foto
des Oloid-Erfinders Paul Schatz nachgehen. Schließlich ist er da nicht mit einen Oloid, sondern einem anderen, kantigeren Gegenstand zu sehen, den er ebenfalls erfunden hat, nämlich einem "umstülpbaren Würfel" oder genauer: dem umstülbaren Teil eines Würfels:
ein Würfel ist in drei Teilkörper zerlegbar
(Animation nach
).
Dabei sind die beiden blauen Teile identisch, und nur der rote ist kontinuierlich umstülpbar:
(Animation ebenfalls nach
)
(Daa dieses Teil sich wie ein Band um den kompletten Würfel herumschlingt, nenne ich es im Folgenden "Würfelgürtel".)
Das anrührendste Beispiel dafür ist
,
also ein sich permanent umstülpender Würfelgürtel, der sich durch dieses Umstülpen langsam fortwärtsbewegt, als wenn es sich durch die Luft "wühlt".
Nun ist es aber nicht so, dass Paul Schatz zwei Gegenstände (Oloid, Würfelgürtel) erfunden hat, die ansonsten nichts miteinander zu tun haben, sondern erst die Beschäftigung mit umstülpbaren Würfeln hat ihn zur Entdeckung des Oloids geführt
(wobei es mich doch wundert, dass Schatz
[der Würfelzerlegung: wie kommt man darauf?]
[das Oloid]
gekommen sein soll).
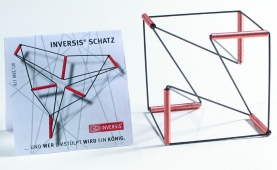
Nun ist der Zusammenhang zwischen Oloid und umstülpbarem Würfelgürtel allerdings nicht einfach zu zeigen und zu begreifen: zumindest für meinen Geschmack ist nämlich das Modell
(von Dr.-Ing. S.Wetzel alias PrismaNN
oder Analemma - eigenes Modell, eigenes Foto, CC BY-SA 3.0 de,
)
wenig überzeugend: wie das Foto zeigt, ist es schon schwierig, das Oloidskelett
(oder gar ein ganzes Oloid)
und den umstülbaren Würfelgürtel gleichzeitig festzuhalten
(zumal letzterer sehr "labbrig" ist).
Um wieviel schwieriger ist es dann aber, den Würfelgürtel kontinuierlich um das Oloidskelett bzw. einen Oloid herumzuführen!
Auch die Erklärung, warum der Würfelgürtel das Oloid "umstreicht", bleibt
(nicht nur für Schüler)
arg abstrakt:
"Die ausgebreitete Kette [= der Würfelgürtel] hat
zwischen gegenüberliegenden Gelenken drei gleich lange Diagonalen. Das
sind die Raumdiagonalen des ursprünglichen Würfels, die auch während
des Umstülpens erhalten bleiben und somit konstante Länge haben. Schatz
beobachtete den Weg, den eine solche Diagonale beim Umstülpen der Kette
nimmt, und entdeckte dabei das Oloid. Fixiert man eines der Tetraeder
und beobachtet den Weg der ihm gegenüberliegenden Diagonale [...], so
erkennt man, dass die von ihr überstrichene Fläche die Oberfläche
(Regelfläche) eines geometrischen Körpers ist, den Schatz Oloid nannte."
(Quelle:
)
Um den Zusammenhang zwischen Würfelgürtel und Oloid anschaulicher zu machen, müsste man komplizierte und mechanisch sehr aufwändige Modelle bauen:
(siehe das Gerät rechts; Quelle:
)
Wegen dieser Schwierigkeiten scheint es mir hier ausnahmsweise eine Computeranimation hilfreich zu sein:
(Animation nach )
Da reicht es natürlich nicht, einfach nur dabei zuzusehen, wie der Würfelgürtel sich um das Oloid windet
(also nur den Effekt zu bestaunen),
sondern zum Verständnis müssten immerhin drei Punkte geklärt werden:
, dass die Diagonale des Würfelgürtels bei all seinen "Verrenkungen" gleich lang bleibt
(s.o. "[...] die Raumdiagonalen des ursprünglichen Würfels, die auch während des Umstülpens erhalten bleiben und somit konstante Länge haben");
, dass die Diagonale
immer die beiden Kanten des Oloids verbindet und dabei alle
Linien in überfährt
(aus 1. und 2.
zusammen folgt - nebenbei gesagt - eine erhebliche Vereinfachung des
Baus von
: die Speichen sind alle gleich lang);
, dass der Würfelgürtel sich beim Umfahren des
Oloids genau einmal à la 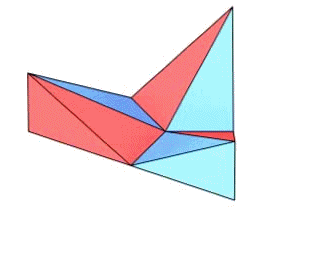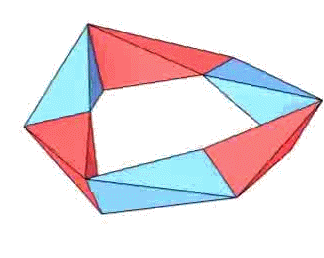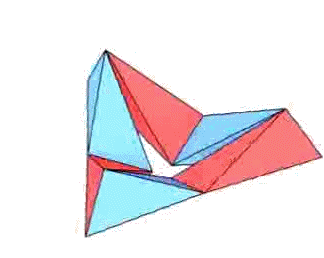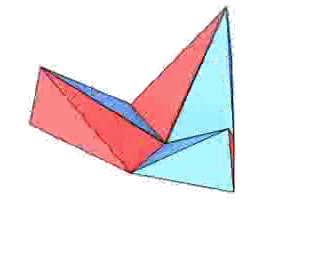umstülpt.
Dabei bleibt (für mich) 1. aber abstrakt: warum
bleibt die Diagonale des Würfelgürtels beim Umstülpen immer gleich lang,
und zwar so lang wie die Diagonale des Gesamtwürfels?
(Ich lasse nicht locker
,
ich will das wissen - und zwar auch, bevor ich Schüler darauf los
lasse. Mir schwant aber
[und sowas ist immer ein bisschen peinlich!],
dass ich bislang nur blind für eine ganz simple Erklärung bin.)
Wenn man das Oloid bereits kennt, ist es nicht mehr allzu schwierig, ein Modell zu bauen bzw. ein Computerprogramm zu schreiben, bei dem sich der Würfelgürtel um das Oloid stülpt.
Paul Schatz musste das Pferd allerdings von hinten aufzäumen: er stülpte den Würfelgürtel um, und erst durch die dadurch entstehende Bewegung der Würfelgürteldiagonale ergab sich die Außenhaut eines bis dahin noch gar nicht existenten Oloids, den er sich als Ganzheit überhaupt erst denken musste. Hat er dazu einen Umstülpmechanismus gebaut - oder hat er sich das alles als eine Art inneren Film vorgestellt
(welch enorme räumliche Vorstellungkraft muss er dann gehabt haben!)?
Es gibt verschiedene Arten, sich wenn schon nicht alle drei Teile in
,
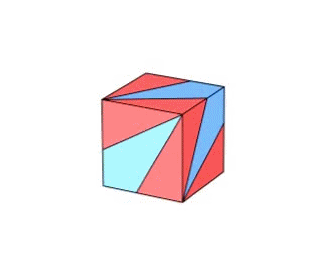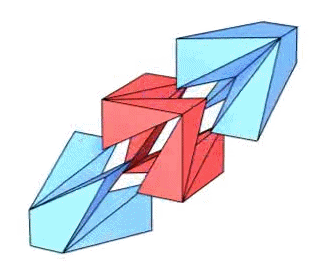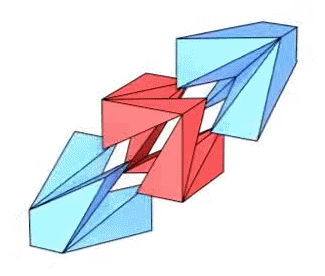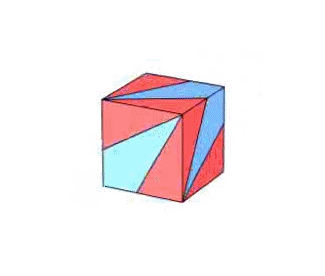so doch den Würfelgürtel zu bauen:
: man kommt wie Paul Schatz "irgendwie" selbst darauf, einen Würfel derart zu zerschneiden:
Dabei versteckt sich das Problem in dem kleinen Wörtchen "irgendwie":
?
All das sind wohl Fragen, die für den Schulunterricht viel zu "hoch" sind, weshalb folgt, dass man die Sache wieder nur "halb" machen kann.
Werden wir also praktischer: wie kann man einen umstülpbaren Würfelgürtel bauen?:
, indem man an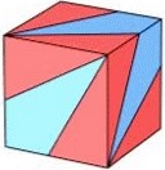 
die Seiten
der roten Dreiecke abmisst
(ohne genauere Erklärung: ein bisschen Satz-des-Pythagoras-Anwendung zeigt: wenn die Seitenkanten des Würfels 1 lang sind, darf die Strecke x
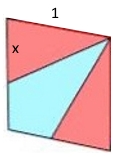
nicht
beliebig lang [ < 1 ] und auch nicht, wie man meinen könnte,
lang sein, sondern muss sie
lang sein, damit die Würfelgürtel-Diagonale
genauso lang ist wie die Würfeldiagonale
und der Würfelgürtel somit tatsächlich das Oloid "abfährt");
, indem man die fertige Vorlage (eine sogenannte "Abwicklung")
(wobei die verschiedenen Farben sehr wichtig sind,
um später beim Umstülpen Übersicht über die Bewegungen zu bekommen)
benutzt.
Bei 1. und 2. ist wohl das Basteln mit Pappe oder - besser noch - verschiedenfarbigem Karton empfehlenswert. Im Folgenden hingegen sind festere Materialien sinnvoll.
: man baut nicht die vollständige Würfelgürtel-Hülle, sondern immer weiter reduzierte "Würfelgürtel-Skelette", die das Umstülpen nur um so anschaulicher machen:
→ 
→ 
→
. Es gibt eine Menge anderer umstülpbarer Körper: ein schöner Fundus für Schüler-Präsentationen
(jetzt endlich mal handfester selbstgemachter Dinge)
ist da
.
Dass eine Oloid-Unterrichtsreihe ganz und gar nicht in die gängigen rigiden Lehrpläne passen würde, war schon oben erwähnt worden. Einer der Haupteinwände gegen solch eine Unterrichtsreihe wäre aber wohl auch: "Wie will man das denn in einer Klassenarbeit abprüfen?"
(Heutzutage läuft ja mehr denn je alles auf Prüfungen hinaus: Hauptsache, es wird »objektiv« geprüft, benotet und dann "gerankt".)
Nun ist es in NRW ja durchaus unter bestimmten Bedingungen erlaubt, einzelne Klassenarbeiten durch anderweitige Schülerleistungen
(Referate, neumodische "Präsentationen", mündliche Prüfungen ...)
zu ersetzen.
Warum also
(wenn schon unbedingt andauernd benotet werden muss)
nicht mal
die engagierte und kreative Mitarbeit der Schüler in einem weitgehend handwerklichen Oloid-Projekt sowie
ihre Beiträge zu einer Oloid-Ausstellung
bewerten?!
Ein weiterer Einwand gegen ein - wie gesagt - weitgehend handwerkliches Oloid-Projekt wäre wohl, was die Schüler dabei eigentlich lernen, womit wohl vor allem gemeint wäre: mathematisch lernen.
Dahinter würde wohl eine rhetorische Frage stecken, denn die indirekt unterstellte Antwort wäre wohl: "Die Schüler lernen [mathematisch] nichts."
Und das würde ja wohl auch stimmen, wenn man
(wie sonst immer im üblichen Mathematikunterricht, wenn man mal von seltenen geometrischen Konstruktionen absieht)
nach abprüfbaren Rechnungen fragen würde.
Dafür würden die Schüler aber was anderes üben:
noch außer-mathematisch: handwerkliche Fähigkeiten; daraus aber folgend:
schon geometrisch-mathematisch: räumliche Vorstellung.
und
zerlegen. Wieder zusammengesetzt, sind diese
beiden Teile
nur durch die 
und 
.
und 
,
