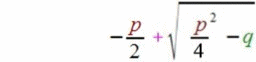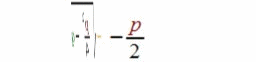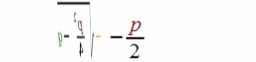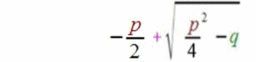
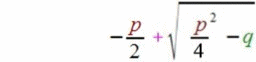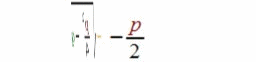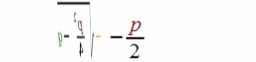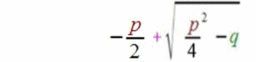
Ich habe ewig (40 Jahre) gebraucht, bis mir urplötzlich (erst vor einigen Tagen) aufging, was 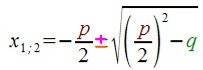 anschaulich bedeutet und welche Folgen das hat:
anschaulich bedeutet und welche Folgen das hat:
von wegen "ewig": kann ich's dann von "meinen" SchülerInneN "verlangen"?
von wegen "anschaulich": könnte es für sie vielmehr sogar eine große Hilfe sein?
Quadratische Gleichungen der Form
![]()
(wenn sie also "normiert" sind, d.h. vor dem x2 nichts bzw. eine 1 steht; und wenn rechts eine Null steht, also die Nullstellen der Funktion gesucht werden)
lassen sich
(wenn sie denn überhaupt lösbar sind)
mittels der p-q-Formel
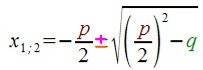
bzw.
(was dasselbe ist)
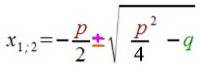
lösen, bzw. mittels dieser Formeln kann man herausfinden,
ob überhaupt Nullstellen vorliegen
und wenn ja, wie viele
und welche.
(Es sei hier nur kurz angedeutet, dass man die p-q-Formeln durch "quadratische Ergänzung" erhält.)
Wichtig an
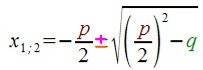
ist nun, dass
im einen Fall die Wurzel
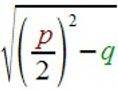 zum Fixwert
zum Fixwert ![]() addiert wird:
addiert wird:
![]() +
+ 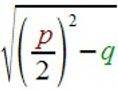 ,
,
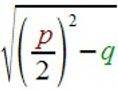 vom Fixwert
vom Fixwert ![]() -
- 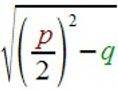 .
.
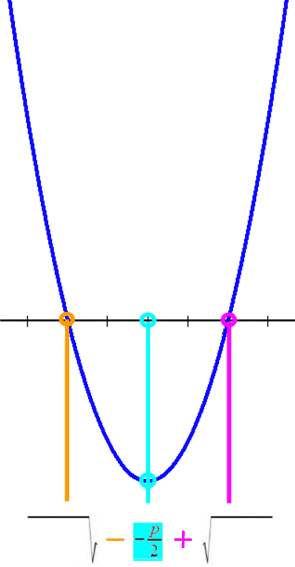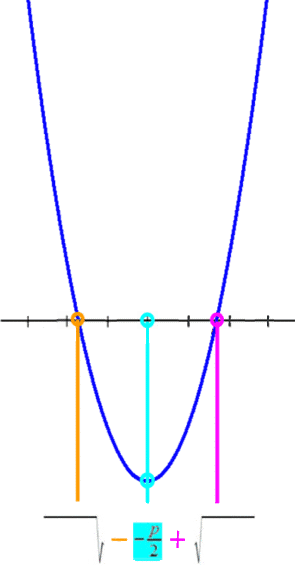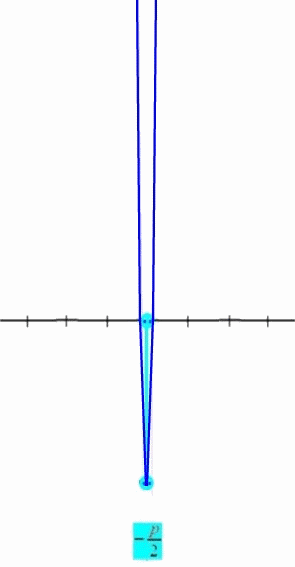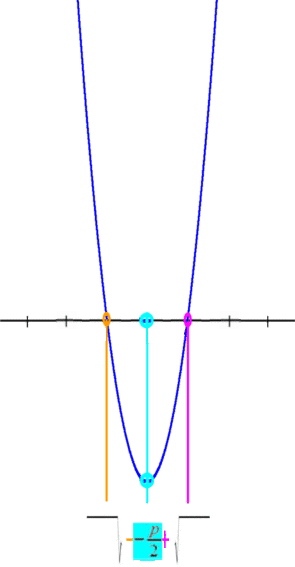
Der Fixwert ![]() ist dabei sozusagen
ist dabei sozusagen

Fels in der Brandung,
um den sich alles andere
(wie wir sehen werden: hübsch symmetrisch)
"dreht".
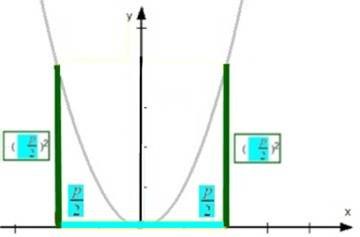
Nun mögen einem die Bruch- und Wurzelwerte ![]() bzw.
bzw. 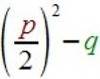 noch arg kompliziert erscheinen, weshalb wir vereinfachen:
noch arg kompliziert erscheinen, weshalb wir vereinfachen:
xxxxx
+

xxxxx

(wobei nur wichtig ist, dass unter beiden Wurzeln dasselbe steht, nämlich 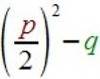 ).
).
Wenn wir a. und b. ein wenig umordnen, erhalten wir
 - xxxxx + - xxxxx +  |
bzw.
bzw.
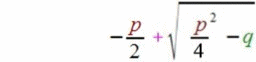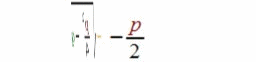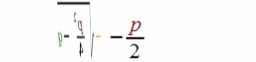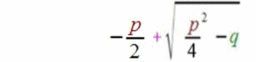

bzw.
Damit ist aus der abgenagten algebraischen Gleichung
(die den Nachteil hat, dass die Wurzel "beides Mal" rechts von ![]() steht)
steht)
eine geometrische Anschauung geworden
Weil wir Menschen geometrische Symmetrie aber oftmals als schön empfinden
ist damit die Gleichung vielleicht auch "schön" geworden
(... womit sich ein ganz anderer [und sehr ergiebiger] Symmetrie- und damit Schönheitsbegriff von Gleichungen andeutet: ![]() ).
).
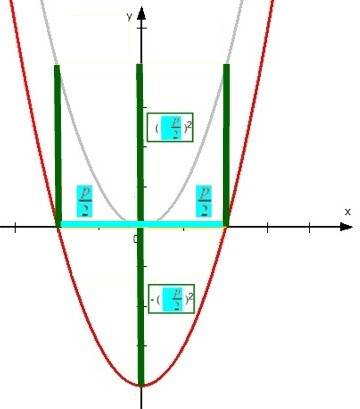
Nun ist ![]() aber nicht nur ein Hilfswert, um die (falls überhaupt vorhanden) Nullstellen
aber nicht nur ein Hilfswert, um die (falls überhaupt vorhanden) Nullstellen 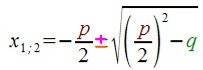 zu berechnen, sondern hat selbst eine fundamentale Bedeutung.
zu berechnen, sondern hat selbst eine fundamentale Bedeutung. ![]() ist nämich der x-Wert des Scheitelpunkts S der Parabel:
ist nämich der x-Wert des Scheitelpunkts S der Parabel:
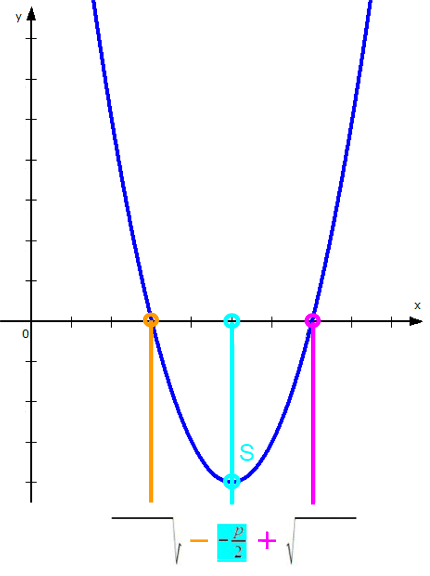
bzw.


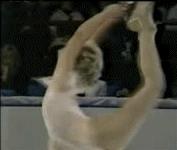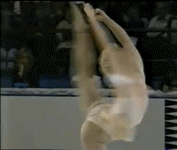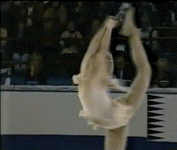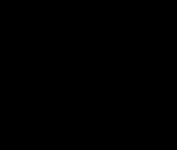
(Nebenbei aus aktuellem Anlass:
Bemerkenswert ist vor allem, dass ![]() ,also der x-Wert des Scheitelpunkts,
,also der x-Wert des Scheitelpunkts,
nur von p aus der Funktionsgleichung f: y = x2 + px + q ,
aber nicht von q abhängt.
Das liegt daran, dass q die Normalparabel nur nach oben bzw. unten verschiebt ↨ , also
wohl die x- und y-Werte der Nullstellen
(falls diese Nullstellen überhaupt existieren)
sowie den y-Wert des Scheitelpunkts verändert,
aber eben nicht den x-Wert
![]() des Scheitelpunkts.
des Scheitelpunkts.
Wenn man also in y = x2 + px + q
p (und damit
![]() ) festhält
) festhält
und nur q verändert,
sieht das so aus:
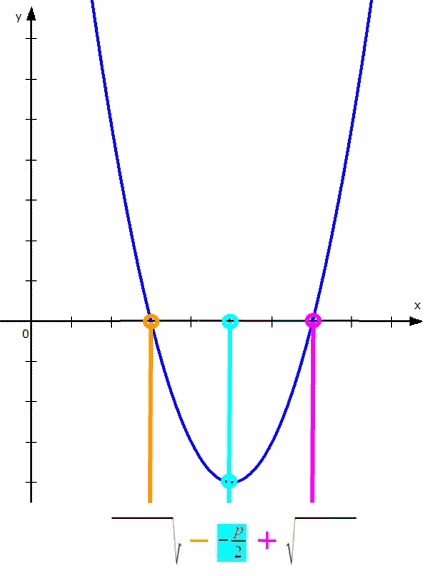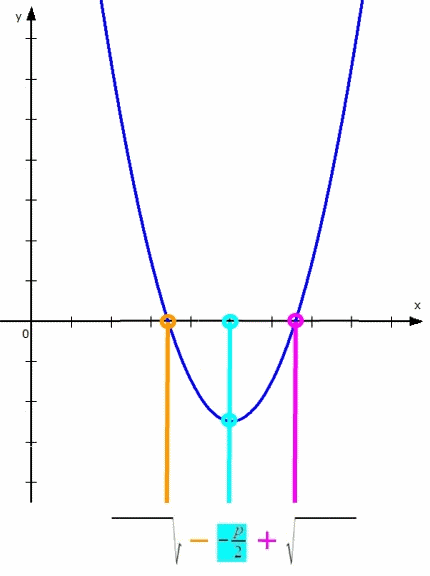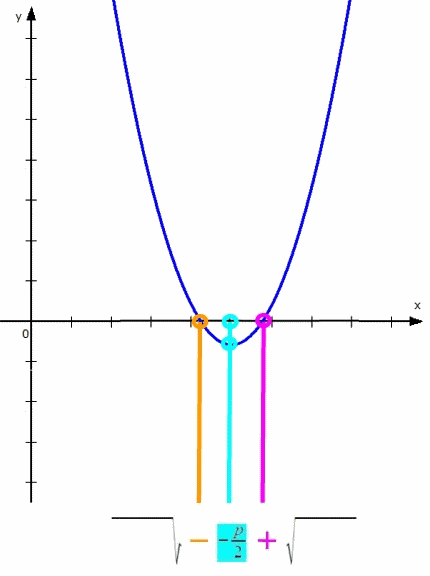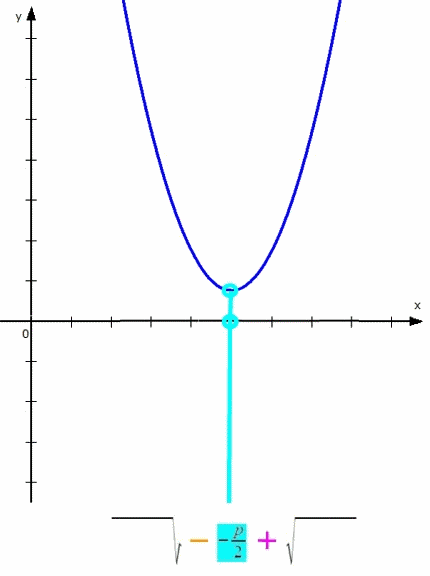
Nun ist
![]() ja schon ein ziemlich abstrakter Wert. Schauen wir uns aber dennoch mal an, wie es zu ihm kommt. Weil wir inzwischen wissen, dass q die Normalparabel nur nach oben oder unten verschiebt, lassen wir q in y = x2 +
px + q einfach mal weg
ja schon ein ziemlich abstrakter Wert. Schauen wir uns aber dennoch mal an, wie es zu ihm kommt. Weil wir inzwischen wissen, dass q die Normalparabel nur nach oben oder unten verschiebt, lassen wir q in y = x2 +
px + q einfach mal weg
(bzw. setzen q = 0).
und erhalten y = x2 + px .
Nun könnte man meinen:
wenn q nur für eine vertikale Verschiebung ↨ sorgt,
wird p wohl nur für eine horizontale Verschiebung ↔ sorgen.
Aber leider ist das ein bisschen komplizierter. Schauen wir uns dazu mal an, wann die vereinfachte Funktion f: y = x2 + px Nullstellen hat:
0 = x2 + p x
![]() 0 = ( x +
p) •
x
0 = ( x +
p) •
x
![]() 0 =
( x +
p)
oder 0 = x
0 =
( x +
p)
oder 0 = x
![]() -
p = x
oder 0 = x .
-
p = x
oder 0 = x .
Die Nullstellen der Funktion f: y = x2 + px sind also N1 (0 | 0 ) und N2 ( - p | 0 ), womit sich folgender Funktionsgraph ergibt:
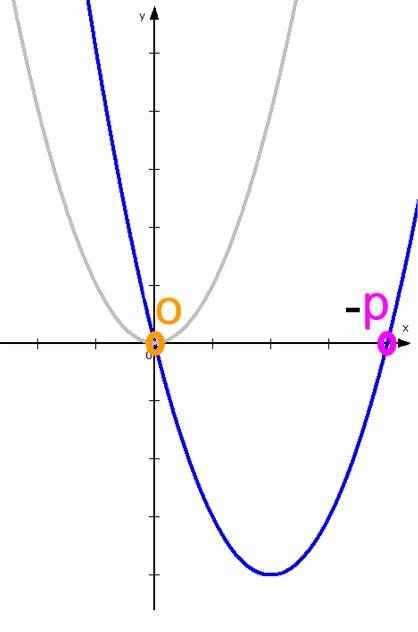
Die Normalparabel ist also schon allein durch das
p nach schräg unten rechts ![]() , also
, also
sowohl horizontal →
(und zwar um
![]() )
)
als auch vertikal ↓ verschoben worden:
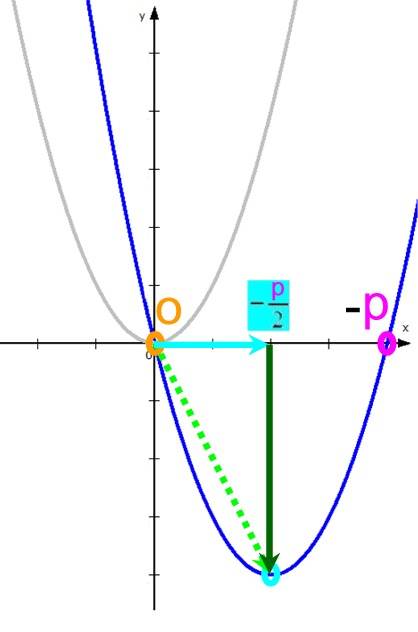
Und damit ergibt sich
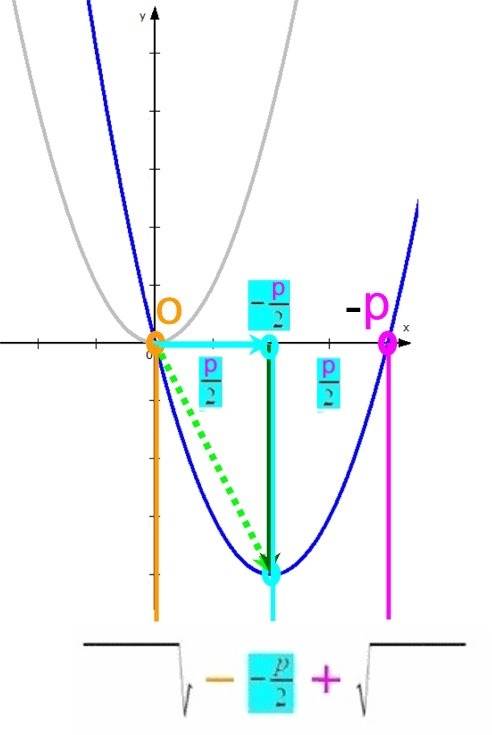
Damit stellt sich aber auch die Frage, wie weit die Normalparabel durch
p nach unten ↓ verschoben wird. Wir erhalten den y-Wert des Scheitelpunktes, indem wir
![]() für x in die Funktionsgleichung
für x in die Funktionsgleichung
f: y = x 2 + p x
einsetzen:
y = (
![]() )2 +
p •
)2 +
p •
![]() =
=
= ![]() -
- ![]() =
=
= 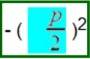
Hier fällt nun auf, dass da dasselbe
![]() auftaucht wie oben in
auftaucht wie oben in 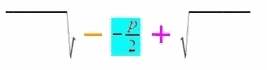 , womit sich die Frage stellt, ob das rechnerischer Zufall ist oder ob da eine "Masche" hinter steckt.
, womit sich die Frage stellt, ob das rechnerischer Zufall ist oder ob da eine "Masche" hinter steckt.
Um das herauszufinden, vereinfachen wir in zwei Schritten:

und erhalten somit überschaubarer
Hier zeigt sich nun aber, dass 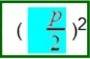 in der Tat der Funktionswert (bzgl. der Normalparabel) von
in der Tat der Funktionswert (bzgl. der Normalparabel) von
![]() ist.
ist.
All diese Überlegungen sind schon arg abstrakt und 
(und damit eigentlich nicht mein Thema hier; aber wo ich schon mal dabei bin ...),
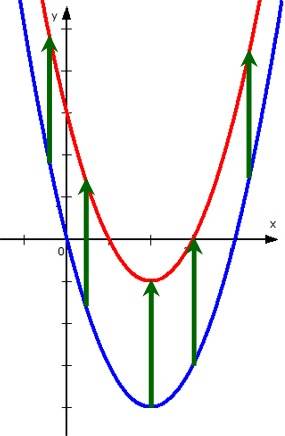
Kommen wir damit kurz zu dem Fall, dass
nun noch die vertikale Verschiebung ↨ durch q hinzu genommen,
also y = x2 + px + q jetzt doch wieder mit q betrachtet,
also die blaue Parabel um q nach oben ↑ verschoben und zur roten wird:
"Kurz", weil für mich das Zustandekommen der Abstände 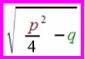 in
in
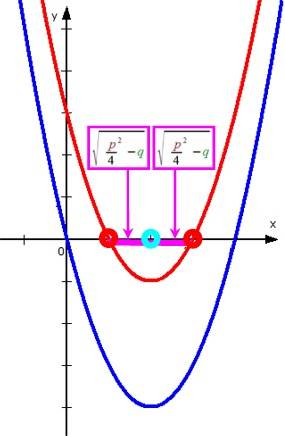
völlig abstrakt bleibt.
Halten wir also vorerst nur fest:
die horizontale Verschiebung → kommt nur durch p zustande,
die vertikale Verschiebung ↨
(und das macht den Umgang mit Parabeln so schwierig)
kommt
sowohl durch p
als auch durch q zustande.
Ich hatte anfangs gesagt, dass mir ewig lange verborgen geblieben ist, was 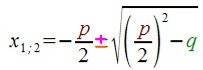 anschaulich bedeutet
anschaulich bedeutet
(nämlich 

 )
)
und welche Folgen das hat:
nämlich die, dass man sich die aus der "Standardform" y = x2 + px + q umständlich
(mittels quadratischer Ergänzung)
herleitbare "Scheitelpunktsform" y = (x - a)2 + b
(wobei a und b die Koordinaten des Scheitelpunkt S ( a | b ) sind)
sparen kann: wenn man die beiden Nullstellen (einfacher!) berechnet hat, liegt der Scheitelpunkt (genauer: sein x-Wert) genau in der Mitte zwischen den beiden Nullstellen
(und überhaupt ist die Scheitelpunktsform ja wenig hilfreich, da sie nur für quadratische, aber z.B. nicht mehr für kubische Funktionen gilt; da warte ich doch lieber auf die "Ableitung", mittels derer man die Extrema aller Funktionen berechnen kann).
Dumm ist's allerdings, wenn eine Parabel gar keine Nullstellen hat - und man den Scheitelpunkt also leider doch mit der Scheitelpunktsform berechnen muss
(oder die Parabel so lange vertikal ↨ verschiebt, bis sie eben doch wieder Nullstellen hat).
(und sollte sowieso wissen, dass bei quadratischen Parabeln im Verborgenen noch eine zweite Nullstelle lauern kann).
die Ableitung einer Funktion dritten Grades ist eine quadratische Funktion:
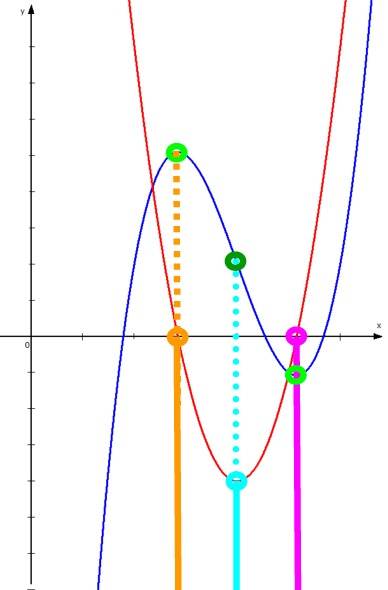
Außerdem gilt:
die Nullstellen
0 und
0 der quadratischen Funktion sind
die Extrempunkte
0 und 0 der
Funktion dritten Grades.
das Scheitelpunkt
0 der quadratischen Funktion ist
der
Wendepunkt
0 der Funktion dritten Grades.
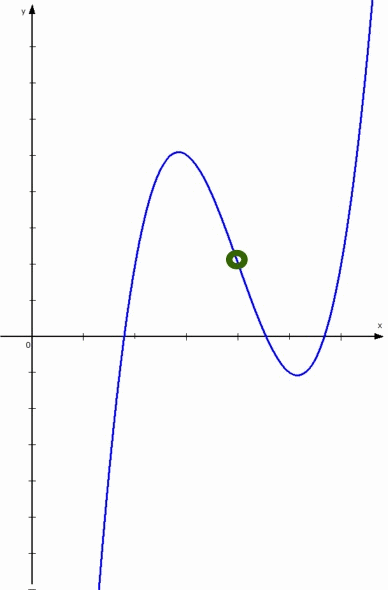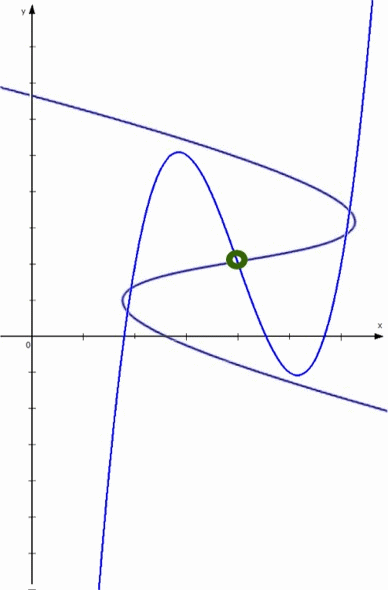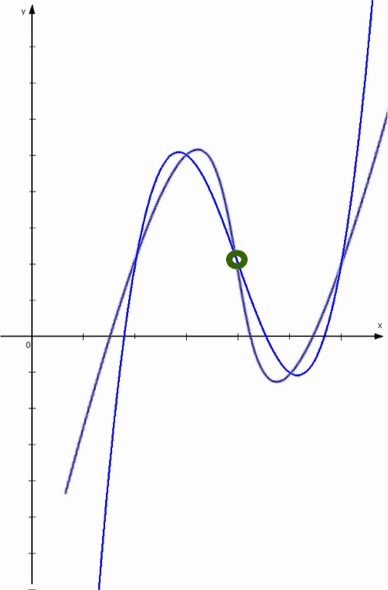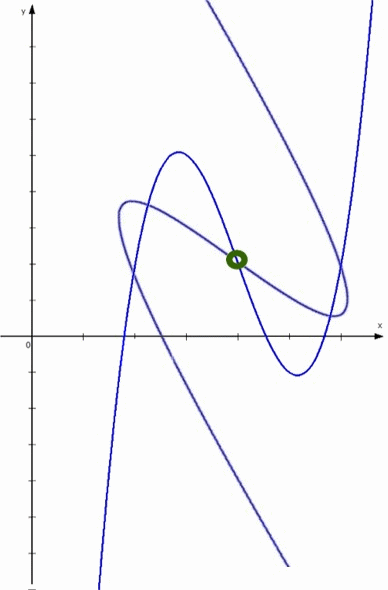
Da nun aber die genannten Punkte der quadratischen Funktion (wie oben gezeigt) achsensymmetrisch liegen,
liegen auch die genannten Punkte der Funktion dritten Grades punktsymmetrisch
(allerdings jetzt nicht mehr achsen-, sondern punktsymmetrisch, und zwar zum Wendepunkt 0 ).
"Punktsymmetrisch" bedeutet aber auch "drehsymmetrisch um 1800", also wieder "Rotation":
(Kleine Ergänzung:
alle Funktionen dritten Grades sind punktsymmetrisch zu ihrem Wendepunkt,
und beim Spezialfall y = ax3 + bx1, wenn also nur ungerade Exponenten auftauchen, liegt der Wendepunkt im Ursprung und ist somit der Funktionsgraph punktsymmetrisch zum Ursprung.)
In Analogie zu quadratischen Funktionen gilt nun auch für Funktionen dritten Grades:
wenn man die beiden Extreme hat
(falls die Funktionen dritten Grades überhaupt Extrema, d.h. wenn die zugehörigen quadratische Ableitungsfunktionen Nullstellen haben),
ergibt sich der Wendepunkt ganz einfach, da er in der Mitte der Extrema liegt;
wenn man ein Extremum und den Wendepunkt hat, ergibt sich das andere Extremum sehr einfach, da es "auf der anderen Seite" des Wendepunkts liegt
(und wieder sollte man wissen: wenn eine Funktion dritten Gerades ein Extremum [z.B. Maximum] hat, muss es auch ein zweites Extremum [dann Minimum] haben).