was heißt und zu welchem Ende studiert man Primzahlgeschichte?

langweilige Vorbemerkungen

die eigentliche Geschichte

langweilige Nachbemerkungen

Vorbemerkungen:

Zu welchem Ende (probeweise mal: wozu) spiele ich mit dem Titel

"was heißt und zu welchem Ende studiert man Primzahlgeschichte?"

auf Schillers jenaer Antrittsrede an?

Einfach nur, um Bildung raushängen zu lassen?

1. , um "was heißt" im Hinblick auf Primzahlen zu klären, also zu zeigen, worum es  bei ihnen  geht

(nicht nur - arg simpel -, was sie sind, sondern auch, was man so alles mit ihnen anstellen kann, ja, welch vielfältige und interessante Fragen sich bei der Beschäftigung mit ihnen fast automatisch einstellen),

2. , um zu vermitteln, "zu welchem [wie wir sehen werden: ungewissen und vielleicht gerade deshalb spannenden] Ende" man sich mit ihnen beschäftigt,

3. , weil für mich die Geschichte der Primzahlforschung ein Königsweg zu ihrem (ansatzweisen) Verständnis (1.), aber auch zum Spaß an eben den Primzahlen ist,

4. , weil  es allemal am überzeugendsten und verständlichsten ist, wenn man GeschichteN über Mathematik erzählt

(was die Geschichten, wie man auf Ideen kommt, aber auch, welche Schwierigkeiten Normalsterbliche genauso wie Fachleute damit haben [und haben dürfen!], impliziert).

Es soll im Folgenden vor allem um den Beweis des Euklid gehen, dass es unendlich viele Primzahlen gibt.

(Es mag übertrieben erscheinen und vielleicht auch fürs zügige Lesen hinderlich sein, wenn ich im Folgenden penetrant "unendlich" mit dem üblichen Symbol und "endlich" mit markiere. Aber so wird eben doch der für die gesamte folgende Argumentation entscheidende radikale Gegensatz besonders deutlich, und zwar vor allem, da beide Wörter sich nur durch die allzu unscheinbare Vorsilbe "un" unterscheiden - und wenn in ein und demselben Satz von beidem die Rede ist.

Eigenartig finde ich es aber allemal, dass

• bei den Wörtern "unendlich" die Negation von "endlich" ist,

• während es bei den Symbolen nur umgekehrt möglich ist, nämlich als Negation von ).

Man spricht auch von "dem" "Satz von Euklid", wodurch signalisiert wird, dass dieser Satz sogar in seinem vor lauter wichtiger mathematischer Erkenntnisse strotzenden Buch "Elemente" etwas ganz Besonderes ist:

dieser bewundernswert einfach-raffinierte Beweis ist einer der absoluten Klassiker der Mathematikgeschichte, und das Buch, in dem er steht, nämlich Euklids "Elemente", ist allemal "der" Klassiker unter allen Mathematikbüchern.

Genau das ist aber das Problem!: diese "Elemente" sind aus drei Gründen richtungsweisend für die gesamte nachfolgende Mathematik geworden:

1. wegen der Fülle der Erkenntnisse, die mit ihnen urplötzlich vorhanden oder zumindest doch erstmals aufgeschrieben waren

(wobei unklar ist, was da von Euklid selbst stammt und welche bereits vorhandenen [von anderen stammenden] Erkenntnisse er "nur" [aber wie!]  gesammelt hat);

und diese Fülle hat die Mathematiker für mehr als 2000 Jahre bis in unsere Gegenwart angeregt und weiterdenken lassen!

2. wegen des glasklaren Aufbaus: da wird "alles" logisch aus ganz wenigen Voraussetzungen (Axiomen) gefolgert! Euklid hat also als erster aus der Mathematik ein stabiles Haus gemacht und damit überhaupt erst "die" Mathematik erschaffen

(wenn auch später - etwa durch Riemann - schöne Bomben an die Fundamente dieses Hauses gelegt wurden);

3. betreibt Euklid eine äußerst knappe, ja, so weit wie möglich abgenagte Mathematik: da folgen in unerbittlichem Nacheinander die nackten Erkenntnisse ohne jegliches "Fleisch an den Knochen" aufeinander.

   Letzteres ist natürlich ungemein praktisch und hat viele Mathematiker durchaus auch ästhetisch fasziniert, war aber in anderer Hinsicht doch auch regelrecht fatal

(wie sehr haben viele Schüler- und Studentengenerationen an dieser Knappheit gelitten, ja, sind sie regelrecht an ihr verzweifelt!):

dieser Art Mathematik

(und es ist leider [!] fast die einzig wahre geworden)

sind jegliche Geschichten

(wer drauf gekommen ist [Namen - und damit Freuden oder Leiden - oder gar ein "ich" interessieren nicht mehr] und wie man drauf kommen kann [erklärenden Zwischenschritte])

gründlich ausgetrieben

(bzw. Euklid erzählt überhaupt nur noch eine rein mathematische Geschichte).

Diese Mathematik hat etwas Unmenschlich-Geisterhaftes an sich bzw. "Operation gelungen, der Patient ist tot". Da muss man vielleicht doch einen ganz speziellen Humor haben, um sowas schön zu finden:

"Mein Gerippe
ist ja so sexy, wenn ich strippe."
(Nina Hagen)

(Und Euklid - um doch endlich einen Sündenbock zu haben - war an solcher Abgenagtheit der Hauptschuldige - wie sonst vielleicht nur noch im 19. Jahrhundert n. Chr. Weierstrass; vgl. )

Die Vor- und Nachteile dieses "Abgenagt-Seins" lassen sich besonders gut eben an Euklids Beweis, dass es unendlich viele Primzahlen gibt, zeigen.

So etwa sinngemäß (wenn auch in modernerer mathematischer "Sprache") lautet dieser Beweis:

"Euklids Klassiker

Annahme: es gibt eine größte Primzahl P. Die Anzahl der Primzahlen ist aufgrund dieser Annahme endlich.

Behauptung: Die Annahme trifft nicht zu.

Beweis: Man konstruiere eine Zahl a wie folgt:

a = 2 · 3 · 5 · 7 · 11 ·... · P + 1

a ist das Produkt aller Primzahlen, vermehrt um 1. Die Zahl a ist offenbar durch keine der Primzahlen teilbar, da bei einer Division von a mit einer Primzahl der Rest 1 bleibt. Folgerung a ist entweder prim oder aus Primfaktoren zusammengesetzt, die ungleich den vorausgesetzten (und damit zwangsweise größer als P) sind. Dies steht im Widerspruch zur Annahme. Folglich ist die Annahme falsch und es gibt unendlich viele Primzahlen."
(zitiert nach )

Da bedenke man vorweg, was der Beweis eigentlich leisten müsste: nämlich zeigen, dass es unendlich viele Primzahlen gibt, also am besten doch unendlich viele nacheinander aufzählen

(es müssen aber nicht unbedingt alle sein, sondern man darf durchaus auch mal welche versehentlich überspringen; auch dann bleiben es unendlich viele).

"unendlich viele Primzahlen nacheinander aufzählen" ist aber per se ausgeschlossen: man könnte zwar hoffnungsfroh anfangen

    2      3     5     7    11   13    17   19   23   29    31   37   41   43   47   53
  59    61   67   71   73   79    83   89   97 101 103 107 109 113 127 131
137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223
227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311
313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503
509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613
617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719
727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827
829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997,

würde aber leider nie fertig - und wüsste, wenn man bei einer riesig großen Primzahlen endlich frustriert aufgäbe, noch immer nicht, ob

• die Primzahlreihe vielleicht tatsächlich (wie vermutet) ewig weitergeht oder
• nicht doch irgendwann aufhört, also endlich ist.

Also fange man doch erst gar nicht an! Zudem ist es gerade in der Mathematik immer zu empfehlen, stinkend faul zu sein und sich schon gar nicht zu übel-schnöder Rechenarbeit herzugeben.

(... denn üble Rechenarbeit steht einem ja spätestens dann bevor, wenn man nachweisen muss, dass eine vermutliche Primzahl auch tatsächlich eine ist: man müsste für jede solche vermutliche Primzahl durchrechnen, ob sie auch tatsächlich durch keine einzige kleinere ganze Zahl [außer natürlich 1] teilbar ist - und das können immerhin auch schon massenhaft Zahlen sein.

Nebenbei:

1. reicht - aber das sei hier nicht genauer erklärt - zum Nachweis, dass eine [Ausgangs-]Zahl tatsächlich eine Primzahl ist, die Division durch alle Zahlen, die kleiner als die Hälfte der Ausgangszahl ist; und ähnlich gibt es weitere Vereinfachungen: wenn beispielsweise eine Zahl nicht durch 2 teilbar ist, dann erspart sich auch die Überprüfung, ob sie durch 4 ... teilbar ist;

vgl. auch das berühmte

"Sieb des Eratosthenes"
[nach ]

2. bringe ich mit meinen Zusatzüberlegungen schon hier - wie es vor allem unten meine Absicht ist -

"Fleisch an die Knochen".)

Ohne nun den Beweis schon genauer anzuschauen

(also ohne ihn schon verstehen zu müssen und - nach dem Verstehen - beurteilen zu können, ob er denn tatsächlich ein [richtiger] Beweis ist),

ist doch eines an ihm

(wenn man überhaupt noch staunen kann)

über alle Maßen bemerkenswert

(und fast für die gesamte Mathematik richtungsweisend bzw. typisch geworden):

Vor-/Entwarnung: meine Version des Beweises dauert erheblich länger (25 Seiten!), ist aber (glücklicherweise!) doch auch endlich :

" ist zwar nicht, wie der Titel androht, unendlich , aber doch um einiges zu lang."

die eigentliche Geschichte:

1. "Was heißen [sind] Primzahlen?"

Diese sicherlich grundlegende Frage lässt sich dennoch (scheinbar) sehr schnell und einfach beantworten

(und ich unterstelle mal, dass, wer auf dieser Seite gelandet ist [sie gezielt gesucht und ausgewählt hat], die Antwort sowieso schon kennt):

Primzahlen nennt man all jene Sonderfälle unter den natürlichen Zahlen 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 ..., die

• nur durch 1 und sich selbst

(die 1 selbst nimmt man allerdings von den Primzahlen aus),

• aber nicht (wie alle sonstigen natürlichen Zahlen) auch durch andere (kleinere) natürlichen Zahlen teilbar sind

(dabei heißt "teilbar", dass "glatt", also ohne Rest wieder eine natürliche Zahl herauskommt).

Zwei Beispiele:

• die 6 ist

  • zwar auch (wie jede natürliche Zahl!) durch 1 und sich selbst (also 8) teilbar, denn

    • 6 : 1 = 6

    • 6 : 6 = 1,

  • aber sie ist zusätzlich auch durch 2 und 3 teilbar, denn

    • 6 : 2 = 3

    • 6 : 3 = 2,

  d.h. die 6 ist keine Primzahl, sondern eine "zusammengesetzte" Zahl;

• die 7 hingegen ist

  • nur durch 1 und sich selbst teilbar, denn

    • 7 : 1 = 7

    • 7 : 7 = 1,

  • aber durch keine andere kleinere natürliche Zahl,

  d.h. die 7 ist eine Primzahl.

Aber vermutlich öde ich die Leser mit solchen, ihnen längst bekannten Banalitäten an - was pure Absicht ist!

Denn "das" kann‘s doch nicht gewesen sein, dafür würde sich doch keinerlei Aufwand (irgendeine Beschäftigung damit) lohnen.

Was also bei dem klassischen Beweis Euklids völlig fehlt (oder stillschweigend vorausgesetzt wird), ist, warum die Primzahlen überhaupt von Interesse sein könnten.

Also nochmals von vorne: "Was heißen [sind] Primzahlen?"

Aber wieso werden Primzahlen die "erste[n] Zahl[en], Ausgangszahl[en], Elementarzahl[en]" genannt?

Es gibt zwei Arten

"Elementarteilchen"

bzw.

"Bausteine des Lebens",

auf denen die halbe Mathematik aufgebaut ist - oder zumindest alle natürlichen Zahlen:

1. die 1, mit der man additiv sämtliche natürlichen Zahlen erhalten kann, nämlich z.B.

1 + 1 + 1 + 1 + 1 + 1 = 6

(Nebenbei: was uns so selbstverständlich erscheint, darüber hat sich Bertrand Russell schier den Kopf zerbrochen.)

2. kann man aber jede natürliche Zahl auch multiplikativ erzeugen, und zwar ausschließlich aus Primzahlen:

Fundamental(!!!)satz der Arithmetik:

Jede natürliche Zahl lässt sich [...] als Produkt von Primzahlen darstellen. Die in dieser Darstellung auftretenden Primzahlen nennt man die "Primfaktoren" der Zahl.

Das sei hier nicht bewiesen - und überhaupt: .

Aber es sei doch an einem einzigen Beispiel erklärt:

12 = 2 • 2 • 3

Hier wurde also die 12 multiplikativ einzig und allein aus Primzahlen (nämlich 2 und 3) erzeugt

(wobei jede Primzahl durchaus mehrfach vorkommen darf).

Allein aus den Primzahlen lassen sich also ALLE natürlichen Zahlen erschaffen!

Und eben deshalb sind die Primzahlen - neben der 1 - die "erste[n] Zahl[en], Ausgangszahl[en], Elementarzahl[en]"!

2. "zu welchem Ende studiert man Primzahlen?"

Nun, wir sind ja noch lange nicht am Ende, aber eben doch schon mitten im Studium der Primzahlen.

Es mag ja stimmen, was der große Mathematiker

Leopold Kronecker
(1823-1891)

gesagt hat:

"Die ganzen [und vor allem wohl die natürlichen] Zahlen schuf der liebe Gott, alles übrige ist Menschenwerk."

Aber das heißt ja nicht, dass das "Menschenwerk" (die anderen, also z.B. rationalen oder irrationalen Zahlen) uninteressant ist (sind). Außerdem sind die ganzen bzw. natürlichen Zahlen (und damit Gott?) doch in ihrer stumpf gleichen Abfolge auch gnadenlos langweilig:

1, 2, 3, 4, 5, 6, 7 und so weiter in alle Ewigkeit!

(Immerhin hat sich Gott am siebten Tag ausgeruht.)

Und beispielsweise die geraden Zahlen als erste Teilmenge der natürlichen sind kaum weniger langweilig:

2, 4, 6, 8, 10 und so weiter in alle Ewigkeit!

Wenn man sich aber eine andere Teilmenge der natürlichen Zahlen, nämlich eben "unsere" Primzahlen, anschaut, stellt man schnell fest, dass sie sozusagen die "Individualisten" unter den natürlichen Zahlen sind:

 2 , 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53 ...

Deutlicher wird diese Individualität an den "Sprüngen":

2 (+1) 3 (+2) 5 (+2) 7 (+4) 11 (+2) 13 (+4) 17 (+2) 19 (+4) 23 (+6) 29 (+2) 31 (+6) 37 (+4) 41 (+2) 43 (+4) 47 (+4) 53 ...

Bei diesen Sprüngen ist zumindest auf den ersten Blick wohl kaum eine klare Regel erkennbar

(darauf wird zurückzukommen sein!).

Die Primzahlen bzw. ihre Sprünge scheinen sich völlig willkürlich zu verhalten.

Immerhin deuten sich aber, auf einen zweiten Blick, schon zwei Trends an:

1. anfangs sind die Sprünge sehr klein, später tauchen auch mal größere Sprünge auf.

Noch deutlicher wird das, wenn man ein bisschen weiter macht, also z.B. bei 113 (+14) 127.

Aber leider (?) zieht diese vermutete Regel (dass also die Sprünge immer größer werden) nicht ganz, denn

2. zwischendurch tauchen öfters sogar auch mal wieder sogenannte "Primzahlzwillinge" auf, also Primzahlen, zwischen denen nur der Sprung 2 liegt.

(Man bedenke, dass die Sprunggröße immer mindestens 2 sein muss, weil zwischen zwei Primzahlen auf jeden Fall eine gerade, also Nicht-Primzahl liegt, z.B. zwischen 3 und 5 die gerade, also Nicht-Primzahl 4.

Kleine Preisfrage zwischendurch: warum sind alle Sprünge immer geradzahlig oder scheinen sie es zumindest auf Anhieb immer zu sein?)

Und solche Primzahlzwillinge gibt es eben keineswegs (wie laut a. zu erwarten) nur im unteren Bereich, sondern beispielsweise auch bei 41 (+2) 43  oder später nochmals bei 857 (+2) 859.

Aus a. und b. lassen sich nun zwei gegenteilige Vermutungen herleiten:

1. lässt vermuten, dass die Primzahlen immer seltener werden - und irgendwann dann völlig aufhören? Dass es also nur endlich viele Primzahlen gibt?

2. hingegen lässt vermuten, dass urplötzlich (und gegen den Trend von a.) doch immer wieder Primzahlzwillinge auftauchen, es also mit den unendlich vielen Primzahlzwillingen auch unendlich viele Primzahlen gibt?

(Man könnte aber auch vermuten, dass die Primzahlzwillinge ebenfalls immer seltener auftauchen, so dass auch sie irgendwann aufhören könnten.

Nebenbei sei schon erwähnt, dass es bis heute ungeklärt ist, ob es unendlich viele Primzahlzwillinge gibt.

... womit ich allerdings [nicht zum ersten Mal] verraten habe, dass es immerhin unendlich viele Primzahlen gibt.)

Die Vermutung "unendlich viele Primzahlen" wird auch gestützt, wenn man beispielsweise die Primzahlen bis 1000 aufschreibt:

    2      3     5     7    11   13    17   19   23   29    31   37   41   43   47   53
  59    61   67   71   73   79    83   89   97 101 103 107 109 113 127 131
137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223
227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311
313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503
509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613
617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719
727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827
829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997

Da wird man nämlich geneigt sein, zu sagen: "Wenn es bis 1000 schon derart viele sind, wird es wohl auch so weitergehen."

(So würde zumindest der "gesunde Menschenverstand" schließen, ja, es wohl nicht mal mehr als Vermutung, sondern längst als Gewissheit ansehen [womit sich auch jeder "Beweis" erübrigen würde]. Ein besserwisserischer Mathematiker würde allerdings einwenden: 997 könnte auch zufällig die letzte Primzahl sein, d.h. nach 1000 käme nie wieder eine, und somit gäbe es endlich viele Primzahlen.)

Womit nun endlich die Frage im Raum steht:

Man kann oftmals nicht hinter sein Vorwissen zurück, bzw. es wäre unredlich (anbiedernd, herablassend), es zu leugnen. Aber Vorwissen

(hier, dass es tatsächlich unendlich viele Primzahlen gibt).

ist häufig allzu suggestiv: man

1. sieht nur noch die Vorteile des allzu Bekannten
2. und kann sich andere (Um-)Wege gar nicht mehr vorstellen

(und ist deshalb blind für Alternativen).

Ich bin also heilfroh, dass es unendlich viele Primzahlen gibt, denn

1. werden sie dadurch nur um so geheimnisvoller,
2. ergeben sich daraus (wie noch zu zeigen sein wird) so unendlich viele herrliche Komplikationen (Folgefragen), denn wenn es
3. nur endlich viele Primzahlen gäbe, wäre damit auch schon sämtliche Primzahlforschung jäh zum Abschluss gekommen: man könnte sie alle nacheinander aufschreiben - und dann abhaken.

Warum ziehe ich dann aber wider besseres (Vor-)Wissen dennoch die Alternative in Betracht, dass es nur endlich viele Primzahlen geben könnte?:

1. , um mögliche historische Wege zur Entdeckung der Unendlichkeit der Primzahlen zu verstehen; und diese Wege sind ja vielleicht auch die des heutigen Laien;
2. , weil - wie wir gleich sehen werden - die  beiden möglichen Wege (endlich oder unendlich viele Primzahlen) erstaunlich nah beieinander liegen.

Die Frage

kann, wenn überhaupt

(und das muss spätestens hier dringend gesagt werden),

vermutlich fast nur theoretisch-innermathematisch interessant sein

(wenn man vielleicht mal davon absieht, dass viele Menschen sich auch weit außerhalb der Mathematik für "das Unendliche" interessieren; vgl. Projekt Unendlichkeit):

wer eh keinen Spaß an Mathematik hat, wird ihn vermutlich auch nicht an Primzahlen haben.

Oder könnte (ganz leise hoffend) eine interessante Darstellung der Primzahlen nicht doch auch zu Interesse an Mathematik (zurück-/ver-)führen?

Das Unendliche ist fast nie in "Anwendungen" brauchbar.

Dafür ein Beispiel aus einem anderen mathematischen Gebiet: mit dem Satz des Pythagoras lässt sich schnell zeigen, dass die Diagonale des einfachsten denkbaren Quadrats, nämlich desjenigen mit der Seitenlänge 1, teuflische lang ist.

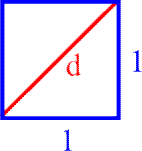
Und ist eben eine irrationale, also hinter dem Komma unendliche (!) sowie - schlimmer noch - nichtperiodische Zahl.

Das lässt sich

(vgl. )

schön beweisen und ist doch nicht "fassbar":

• in der Dezimalschreibweise ist ≈ 1,4142135623730950488016887242097, aber nichtmal der beste Großrechner der Welt wird jemals alle Nachkommastellen berechnen können, da ja unendlich viele davon vorliegen und wegen der Nicht-Periodizität nicht mal die Abkürzung über Brüche möglich ist;
• in jeder nur irgendwie denkbaren Anwendung ist der exakte Dezimalwert von völlig uninteressant, denn
  • beispielsweise einen 1 m ● 1m großen Tisch wird man eh niemals absolut exakt herstellen können (und wollen),
  • ebenso kann man die Diagonale nicht absolut exakt messen,
  • wüsste ich auch keine Situation, in die die Länge der (zudem noch exakt gemessenen) Diagonale von Interesse sein könnte,
  • gibt es auch physikalische Grenzen: irgendwann kommt das allerletzte Atom der Diagonalen, kommen also keine weiteren Nachkommastellen mehr.

In der modernen Physik tauchen allerdings (etwa bei sogenannten "schwarzen Löchern") tatsächlich Unendlichkeiten (sogenannte "Singularitäten") auf, aber das ist dann immer nur ein untrügliches Zeichen dafür, dass die Physiker (zumindest vorerst) mit ihrem Latein am Ende sind. Bzw. da wirds dann erst so richtig interessant!

Und dennoch gilt all das nur unter den Einschränkungen "vermutlich fast nur" und "fast nie". Die Primzahlen sind sogar das einzige Beispiel, bei denen ich, wenn es unendlich viele von ihnen gäbe, wirklich eine (indirekte) Anwendbarkeit wüsste: wenn es unendlich viele Primzahlen gäbe, stünde damit auch ein unendliches Reservoire für die Verschlüsselung von Botschaften (wohl das Hauptanwendungsgebiet von Primzahlen) zur Verfügung (s.u.).

Je nach Vermutung (endlich oder unendlich viele Primzahlen) ergeben sich zwei (anfangs) unterschiedliche Beweiswege:

• erste Vermutung (und erster Irrweg): es gibt endlich viele Primzahlen:

Was wäre eigentlich (auf den ersten Blick) zu tun, um dies zu beweisen?:

Es reicht leider (wie schon gezeigt) nicht, einfach (?) alle bekannten Primzahlen

(z.B. wie oben bis 1000)

aufzuschreiben, denn man könnte ja nur fälschlich meinen, dass danach keine weiteren Primzahlen kommen

(und in der Tat ist 1009 die erste Primzahl über 1000).

Zudem könnte sich das Problem ergeben, dass es zwar endlich viele, aber dennoch abertrilliarden Primzahlen gibt, die nichtmal ein Großrechner herausfinden könnte

(siehe nur den enormen Aufwand beim Versuch, besonders große Primzahlen zu finden [ ]; und wir werden unten noch andere Beispiele dafür sehen, welch enorme Schwierigkeiten sogar Großrechner mit Primzahlen haben).

Nein, das eigentliche Problem bestünde darin, dass man beweisen müsste, dass nach einer (angeblich) größten Primzahl niemals wieder Primzahlen folgen, was aber doch heißt: man müsste für alle Zahlen, die größer als die vermutete größte Primzahl (z.B. 997) sind, nachweisen, dass sie keine Primzahlen sind. Und diese "alle" Zahlen sind eben noch immer unendlich viele.

Um also Endlichkeit zu beweisen, müsste man dennoch unendlich viele Fälle untersuchen

(und jeden einzelnen mit gigantischem Aufwand).

Und das eben ist schlichtweg ausgeschlossen: man (auch ein Großrechner) würde ja mit dem Rechnen nie fertig.

• zweite Vermutung (und zweiter Irrweg): es gibt unendlich viele Primzahlen:

Was wäre eigentlich (auf den ersten Blick) zu tun, um dies zu beweisen?:

Man müsste eben eine unendliche Primzahlliste anlegen

(und für jede einzelne mit gigantischem Aufwand nachweisen, dass sie tatsächlich eine Primzahl ist).

Auch das ist schlichtweg ausgeschlossen: man (auch ein Großrechner) würde ja auch in diesem Fall mit dem Rechnen nie fertig.

Da stellt sich doch die bittere Frage, ob es nicht so oder so aussichtslos ist, einen Beweis zu finden, ob also die Frage nach der Anzahl der Primzahlen nicht schlichtweg unbeantwortbar ist.

Lange Zeit und durch viele Erfolge verwöhnt waren die MathematikerInnen wirklich der Meinung, dass jedes mathematische Problem früher oder später gelöst werden könnte - bis dann Kurt Gödel gezeigt (bewiesen!) hat, dass es auch in der (allzu selbstsicheren) Mathematik Probleme gibt, die prinzipiell nicht entscheidbar sind. Mehr noch: Alan Turing hat sogar bewiesen, dass man das den Problemen leider nicht vorher ansehen kann

(dass an einigen Problemen also leider kein Schild dransteht: "Ich bin unlösbar, und deshalb: versuche es erst gar nicht!"):

• entweder wird ein Problem tatsächlich irgendwann gelöst,
• oder es bleibt eben unklar, ob es  überhaupt lösbar ist.

In letzterem Fall besteht aber die Gefahr, dass man sich ewig lange mit dem Problem beschäftigt, ohne zu ahnen, dass es unlösbar ist.

(Zu Gödel/Turing siehe auch den wunderbaren Mathematikroman von Apostolos Doxiadis: Onkel Petros und die Goldbachsche Vermutung; Lübbe.)

Sollte man da nicht mit Dantes "Göttlicher Komödie" frühzeitig weise resignieren und sich sagen?:

"Lasst, die ihr eintretet, alle Hoffnung fahren!"

Wieso haben die MathematikerInnen (Euklid) dann dennoch versucht, das Problem "Anzahl der Primzahlen" zu lösen? Vielleicht einfach deshalb, weil sie schon viele andere Probleme gelöst hatten - und darunter eben auch welche, die ebenfalls von unendlich vielen Fällen handeln.

Nur zwei Beispiele aus der Zeit vor Euklid:

1. der Beweis, dass die Winkelsumme in allen (ebenen) Dreiecken 180⁰ beträgt. Und "alle Dreiecke" sind eben unendlich viele!
2. der Beweis des "Satzes des Pythagoras", dass also in allen rechtwinkligen Dreiecken a² + b² = c² gilt.
   Nun sind die rechtwinkligen Dreiecke zwar nur eine "kleine" Teilmenge von allen (unendlich vielen) Dreiecken, aber es gibt doch eben auch von diesen nur-rechtwinkligen Dreiecken unendlich viele!

Entscheidend an beiden (hier nicht vorgeführten) Beweisen ist, dass sie paradoxerweise in endlich vielen Schritten (wenigen Zeilen) durchgeführt werden können, obwohl sie doch von unendlich vielen Fällen ([rechtwinkligen] Dreiecken) handeln.

Das muss für die alten Griechen eine geradezu erschütternde Entdeckung gewesen sein - und eine ungeheure Ermutigung bzw. ein grandioses Versprechen! Ja, damit war die Mathematik als die einzige Wissenschaft etabliert, die (wie wir seit Goedel wissen: nur scheinbar) ALLES und für ALLE, ja sogar für UNENDLICH VIELE Fälle beweisen kann.

Mit der Winkelsumme und dem Satz des Pythagoras stand also die Verheißung bzw. Ermutigung im Raum, dass man das Problem "Anzahl der Primzahlen" wohl auch irgendwie in endlich vielen Schritten "erschlagen" könnte.

Hier nun etwa beginnt endlich der eigentliche Beweis des "Satzes von Euklid" - und sind wir

• für MathematikfreundInnEn bei einem der Highlights der gesamten Mathematik,
• für MathematikhasserInnen hingegen vermutlich eher im .

Aus den Beweisen zur Winkelsumme bzw. dem "Satz des Pythagoras" kann man auch lernen, dass sie nur deshalb in endlich vielen Schritten beweisbar sind, weil da nie konkrete Maße (außer im zweiten Fall die Rechtwinkligkeit) benutzt werden.

Und auch die beiden o.g. Irrwege weisen darauf hin, dass man mit dem Versuch, alle (seien es endlich oder unendlich viele) konkreten Primzahlen aufzuzählen, nur scheitern kann.

Es steht also der Tipp im Raum,

• gar nicht mit konkreten Primzahlen, also

2, 3, 5, 7, 11 ...,

anzufangen,

• sondern allgemein vorzugehen:
  • p ₁    (= erste         Primzahl, von der wir noch wissen, dass es 2 ist),
  • p ₂    (= zweite       Primzahl, von der wir noch wissen, dass es 3 ist),
  • p ₃    (= dritte         Primzahl, von der wir noch wissen, dass es 5 ist),
  • ...
  • p ₁₀   (= zehnte      Primzahl, von der ich nicht mehr auf Anhieb weiß, dass es 29 ist),
  • ...
  • p ₁₀₀ (= hunderste Primzahl, von der ich ohne Nachschlagen in einer Primzahltabelle
                                                  nun wirklich nicht mehr weiß, welche es ist, ja nichtmal
                                                  mehr die Größenordnung ahne),
  • ...
  • p _n     (= n-te          Primzahl)

Und nun kommen die beiden Vermutungen von oben zum Tragen:

• erste Vermutung: man ist tatsächlich (und, wie gezeigt, mit guten Gründen) der Meinung, dass es nur endlich viele Primzahlen gibt, wenn man auch nicht weiß, wie viele es sind.

Mit der soeben gefundenen Schreibweise sieht dann die Primzahlliste also so aus:

p ₁, p ₂, p ₃ ... p ₁₀ ..., p ₁₀₀ ...p _n

bzw. kürzer und vollends allgemein:

p ₁, p ₂, p ₃ ...                        p _n .

Entscheidend dabei ist:

1. kommen in der Liste tatsächlich ausnahmslos alle (wenn auch unbekannten) Primzahlen vor - wohlgemerkt unter der Voraussetzung, dass es "nur" endlich viele (wenn auch vielleicht abertausend) sind.

Man muss sich aber mal deutlich machen, wie ungeheuerlich ist, was hier stattfindet: wir hantieren beim vorliegenden Beweis dreist mit ausnahmslos allen (wenn auch endlich vielen) Primzahlen und müssen dabei doch keine einzige kennen. Bzw. jeder kennt ja wohl die ersten, also 2, 3, 5, 7, 11 ..., aber wir reden problemlos auch über den restlichen Rattenschwanz.

2. ist die Liste trotz der Pünktchen leicht handhabbar und überschaubar, da sie

(anders als eine Liste konkreter Primzahlen)

sehr regelmäßig gebaut ist

(was daran liegt, dass die Primzahlen auf wahrhaft genial einfache Art mittels 1, 2, 3 ... abgezählt, also auf die einfachen natürlichen Zahlen reduziert wurden;

da sei doch unbedingt erwähnt, dass dieses Abzählen schwieriger Zahlen, also die Reduktion auf natürliche Zahlen, ein ungemein wichtiger mathematischer Trick geworden ist; vgl.   );

3. ist die Liste wegen der Pünktchen sehr kurz, obwohl damit doch abertausende (aber doch endlich viele) Primzahlen gemeint sein können;
4. muss man gar nicht wissen, was n ist

(ob also die 10te oder 100ste oder ... Primzahl die größte ist),

sondern es reicht, dass n irgendeine natürliche (aber endliche !) Zahl ist.

Anders gesagt: man muss nur von der Voraussetzung ausgehen, dass es endlich viele Primzahlen gibt, aber nicht wissen, wie viele es sind. Und schon gar nicht muss man alle Primzahlen bis hin zur größten kennen

(und durch umständliche Rechnungen gezeigt haben, dass sie alle  tatsächlich Primzahlen sind).

Man könnte insgesamt also sagen, dass man die Wahl zwischen Pest und Cholera hat:

• eine Liste echter Primzahlen (also 2, 3, 5, 7, 11 ...) ist
  • konkret,
  • aber wegen der unregelmäßigen Anordnung der Primzahlen völlig chaotisch,
• die Liste p ₁, p ₂, p ₃ ...p _n hingegen ist
  • völlig abstrakt

    (man weiß nichtmal mehr, von welchen Primzahlen die Rede ist), 

  • dafür aber völlig regelmäßig gebaut.

  Und sie hat gegenüber der ersten, konkreten Liste den unschätzbaren Vorteil, dass ich die größte (wenn auch unbekannte) Primzahl (wenn auch nur sehr allgemein) mit p _n benennen kann.

  Das ja eben macht Abstraktion aus: dass sie

• unter Absehen von irritierenden Einzelfällen (und damit auch Konkretheit)
• klare(re) Strukturen herausarbeitet bzw. sichtbar macht.

• zweite Vermutung: man ist (wieder mit guten Gründen) der Meinung, dass es unendlich viele Primzahlen gibt.

Mit unserer neuen Schreibweise ergibt sich dann die nun unendliche Primzahlliste

p ₁, p ₂, p ₃ ...p _n ...

 oder - da der Zwischenwert p _n nun ja beliebig, also uninteressant ist - verkürzt

p ₁, p ₂, p ₃          ...

Aber diese abschließenden Pünktchen ... sind doch reichlich wenig hilfreich: man weiß nur, dass es nach ein und derselben Masche ewig weiter gehen wird.

Keine Ahnung, wie es in der historischen Entwicklung tatsächlich weiter gegangen ist

(Euklid ist ja der "Hauptschuldige" dafür, dass alles Menschliche verschwiegen wurde; s.o.).

Aber vorstellbar wären doch drei Möglichkeiten:

1. Man hantiert, weil man eine endliche Anzahl von Primzahlen vermutet, mit p ₁, p ₂, p ₃ ...p _n rum.
2. Man hantiert, obwohl man eine unendliche Zahl von Primzahlen vermutet, dennoch vorerst mit der praktischeren endlichen Darstellung p ₁, p ₂, p ₃ ...p _n  rum:

1. einfach, weil man mit allen "unendlichen" Beweisversuchen nicht weiter kommt,
2. , um vorweg an endlich vielen Beispielen noch etwas mehr über das Verhalten von Primzahlen zu erfahren (s.u.),
3. , weil einem die indirekte Vorgehensweise, von der unten die Rede ist, schon von anderen Beispielen, bei denen sie hilfreich war, bekannt ist.

Früher (bei der ersten Vermutung) oder später (bei der zweiten Vermutung) ist man also bei der endlichen Darstellung p ₁, p ₂, p ₃ ...p _n , und deshalb war oben schon gesagt worden, dass sich die beiden Beweiswege nur anfangs unterscheiden.

Wie schon gesagt: hantieren wir doch einfach erstmal nur eine Weile lang mit p ₁, p ₂, p ₃ ...p _n rum

... und erinnern uns dabei daran, dass die Primzahlen insbesondere zur multiplikativen "Primfaktorzerlegung" (s.o.) sämtlicher natürlicher Zahlen geeignet sind.

Da liegt es nahe, sämtliche Primzahlen p ₁, p ₂, p ₃ ...p _n miteinander zu multiplizieren, wobei eine Zahl herauskommt, die wir mal "m" nennen:

m        = p ₁ ● p ₂ ● p ₃ ● ...● p _n .

Kleiner, aber wichtiger Einschub: für unsere Argumentation unten ist es ungeheuer wichtig, dass es wirklich sämtliche Primzahlen sind, d.h. wir dürfen keine einzige vergessen. Aber das ist ja auch kein Problem, weil wir glücklicherweise nicht mehr von konkreten, sondern von hübsch ordentlich durchnummerierten Primzahlen sprechen.

(Nebenbei: wie bei den Primzahlen p ₁, p ₂, p ₃ ...p _n müssen wir auch von m gar nicht wissen, welche konkrete Zahl dahinter steckt!)

Offensichtlich ist diese Zahl m so konstruiert, dass sie eben in die Primfaktoren p ₁, p ₂, p ₃ ...p _n zerlegbar ist. Und somit ist m keine Primzahl.

Das war ja auch deshalb zu erwarten, weil wir mit p ₁, p ₂, p ₃ ...p _n bereits alle Primzahlen hatten, ihr Produkt also nicht nochmals eine Primzahl sein kann.

Wir wissen immerhin, dass es sehr, sehr viele Primzahlen p ₁, p ₂, p ₃ ...p _n gibt. Also muss m als Produkt all dieser Primzahlen schon enorm groß sein. Und insbesondere ist m laut Konstruktion erheblich größer als die größte Primzahl p _n, denn m ist ja ein Vielfaches von  p _n

(nämlich p _n mit sämtlichen kleineren Primzahlen multipliziert).

Erinnern wir uns nun aber daran, was wir vorhaben: wegen der Vermutung, dass es endlich viele Primzahlen gibt, müssen wir zeigen, dass es nach der größten Primzahl p _n keine weitere Primzahlen mehr gibt.

Wir müssen uns also eigentlich sämtliche Zahlen, die größer als  p _n sind, daraufhin anschauen, ob sie nicht vielleicht doch Primzahlen sind. Eine dieser "größeren" Zahlen ist, wie gezeigt, m, von der wir aber wissen, dass sie keine Primzahl ist.

Hier nun aber folgt der ebenso simple wie, so scheint mir, geniale Trick

(ich bezweifle mal, dass ich da jemals alleine drauf gekommen wäre):

man fragt sich nach der nächstgrößeren natürlichen Zahl, also m + 1. Nennen wir sie mal r. Dann gilt

r =                m                      + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● ...● p _n ) + 1

(Kleiner Einschub: es ist doch allemal interessant, wie die MathematikerInnen sich die Zahlen m und r "zurechtkonstruieren". Aber das heißt ja nicht, dass sie sich die "Wirklichkeit" "hinbiegen", sondern nur, dass sie die vorhandenen Freiheiten nutzen!)

Gönnen wir uns nun aber nach so viel Allgemeinheit erst mal eine Verschnaufpause, indem wir das soeben Gesagte anhand einiger Beispiele konkretisieren.

Wir stellen uns also mal dümmer, als wir sind, und behaupten dreist, dass es nicht nur endlich viele Primzahlen, sondern nur genau ganz wenige.

• erste und einfachste Möglichkeit: es gibt überhaupt nur zwei Primzahlen, nämlich die ersten beiden, also

2 und 3.

Damit ergibt sich m = 2 ● 3 = 6.

Nun ist 6 offensichtlich keine Primzahl:

• zwar ist sie (wie jede natürliche Zahl) auch durch 1 und sich selbst (also 6) teilbar,
• aber eben auch durch andere Teiler, nämlich 2 und 3.

Nun ergibt sich

r =   m     + 1 =

  = 2 ● 3 + 1  =

  =    6     + 1 = 7

Da sieht man auf Anhieb, dass das Ergebnis r = 7 jetzt doch eine Primzahl ist.

Dieses scheinbar harmlose Ergebnis muss man sich doch mal auf der Zunge zergehen lassen!:

• Voraussetzung: es gibt nur zwei Primzahlen (2 und 3)
• Folgerung       : es gibt        drei  Primzahlen (2 und 3, aber eben auch 7)!

Das ist doch ein glatter Widerspruch , und also muss die Voraussetzung falsch gewesen sein

(... was uns ja nicht erstaunt, weil wir ja längst wussten, dass es sehr viel mehr Primzahlen als nur 2 und 3  gibt).

• zweite Möglichkeit: es gibt überhaupt nur drei Primzahlen, nämlich die ersten drei, also

  2, 3 und 5

  (wir stellen uns hier sozusagen doppelt dumm, sehen also davon ab, dass wir eben schon kurz die Primzahl 7 hergeleitet hatten).

  Damit ergibt sich m = 2 ● 3 ● 5 = 30.

  Nun ist 30 offensichtlich keine Primzahl:

  • zwar ist sie (wie jede natürliche Zahl) auch durch 1 und sich selbst (also 6) teilbar,
  • aber eben auch durch andere Teiler, nämlich 2, 3 und 5 sowie - was hier aber nebensächlich ist - noch einige andere "Spaltprodukte", die keine Primzahlen sind (6, 10, 15).

  Nun ergibt sich

  r =       m        + 1 =

    = 2 ● 3 ● 5  + 1  =

    =       30       + 1 = 31

  Da sieht man ziemlich schnell, dass das Ergebnis r = 31 jetzt doch eine Primzahl ist .

  Analog zu oben gilt:

  • Voraussetzung: es gibt nur drei Primzahlen (2, 3 und 5)
  • Folgerung       : es gibt        vier Primzahlen (2, 3 und 5, aber eben auch 31)!

  Das ist wieder ein glatter Widerspruch , und also muss die Voraussetzung falsch gewesen sein.

So langsam kann man eine Doppelvermutung aufstellen, die es wahrhaft in sich hat:

1. Vermutung: dieses Verfahren funktioniert immer, d.h. mit

r =                m                           + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● ...● p _n ) + 1

erhalten wir für r immer eine zusätzliche Primzahl p _n+1, ist also die jeweilige Voraussetzung, dass es nur n Primzahlen gibt, FALSCH. Daraus aber würde folgen, dass es NICHT ENDLICH viele ( n) Primzahlen gibt, woraus wiederum folgt, dass es UNENDLICH viele Primzahlen gibt.

2. Vermutung: mit

r =                m                           + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● ...● p _n ) + 1

haben wir ein todsicheres Verfahren, um zu jeder Zahl n eine zugehörige Primzahl p _n+1 zu berechnen.

Nehmen wir das nächst-beste Beispiel n = 4, d.h. wir gehen von den ersten vier Primzahlen 2, 3, 5 und 7 aus. Dann ergibt sich

r =                m                           + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● p ₄       ) + 1 =

 = (  2    ●   3  ●   5   ●   7       ) + 1 =

 =                210                       + 1 =

 =                211

Und 211 ist - es wundert uns schon gar nicht mehr - auch wieder eine Primzahl !

Nochmals: es sieht also schwer danach aus, dass wir mit

r =                m                           + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● ...● p _n ) + 1

ein Verfahren gefunden haben, um zu jedem n eine zugehörige Primzahl r zu finden.

Wenn dieses Verfahren aber immer funktionieren würde, hätte das schier unglaubliche Folgen:

1. könnten wir damit zu jedem beliebigen n eine zugehörige Primzahl r konstruieren, und da es unendlich viele n gibt, könnten wir also unendlich viele Primzahlen konstruieren, womit dann auch bewiesen wäre, dass es tatsächlich unendlich viele Primzahlen gibt!
2. könnten wir dann (scheinbar) mit einem einzigen Rechenverfahren (einer Funktion!) systematisch sämtliche Primzahlen direkt berechnen

(die Rechenarbeit überließen wir einem Großcomputer).

Allerdings nur "scheinbar" denn das Verfahren hat den kleinen Schönheitsfehler, dass wir zwar anscheinend nacheinander massenhaft Primzahlen erhalten, aber zumindest bisher sogar noch sehr viel mehr übersehen haben: bisher haben wir nämlich 

• für n = 2 die Primzahl 7    ,
• für n = 3 die Primzahl 31  ,
• für n = 4 die Primzahl 211,

erhalten, aber alle grau unterlegten Primzahlen übersprungen:

    2      3     5     7    11   13    17   19   23   29    31   37   41   43   47   53
  59    61   67   71   73   79    83   89   97 101 103 107 109 113 127 131
137 139 149 151 157 163 167 173 179 181 191 193 197 199 211

Wiederum das nächst-beste Beispiel, nämlich für n = 5, ergibt

r =                m                                + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● p ₄ ● p ₅ ) + 1 =

 = (  2    ●   3  ●  5    ●   7  ●  11 ) + 1 =

 =                2310                         + 1 =

 =                2311

Und 2311 ist auch wieder eine Primzahl !

Einige LeserInnen werden sich inzwischen aber vielleicht fragen, woher ich eigentlich weiß, dass so eine große Zahl wie 2311 eine Primzahl ist.

Nun, es gibt halt Primzahltabellen oder entsprechende Internetseiten (vgl. etwa ).

Einerseits ist man wohl drauf angewiesen, diesen Primzahllisten zu vertrauen, kann also nicht jedes ihrer Ergebnisse mühsam überprüfen. Und dennoch könnten da ja Druck- und Rechen-/Programmierfehler drin stecken.

So langsam wird es langweilig: wiederum das nächst-beste Beispiel, nämlich für n = 6, ergibt

r =                m                                        + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● p ₄ ● p ₅ ● p ₆ ) + 1 =

 = (  2    ●   3  ●   5   ●   7  ● 11  ● 13 ) + 1 =

 =                30030                                + 1 =

 =                30031

Und diese Zahl 30031 wird doch wohl auch eine Primzahl sein! Eben - man höre und staune! - NICHT: 30031 ist KEINE Primzahl mehr, denn

                   30031 = 59 ● 509

(Nochmals: das sieht wohl kaum einer auf Anhieb, aber das kann man ja nachschlagen.)

Hier gehen also mit einem einzigen Gegenbeispiel all unsere ach so schönen Vermutungen den Bach runter! Darauf wird gleich zurückzukommen sein. Zwischendurch aber noch etwas anderes:

Für n = 7 ergibt sich r = 510511, für n = 8, ergibt sich r = 9699691, und für n = 9 ergibt sich r = 223092871, und all diese r sind ebenfalls KEINE Primzahlen mehr.

Damit ist aber nicht gesagt, dass das Verfahren

r =                m                            + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● ...● p _n ) + 1

nie wieder Primzahlen ergibt. Sondern halten wir vorsichtshalber mal fest:

das Verfahren hat zwei Nachteile:

1. erwischen wir damit, wie bereits oben gezeigt, nicht alle Primzahlen

(z.B. auch nicht, wie soeben gezeigt und ungeheuer wichtig, 59 und 509),

2. ergeben sich für r nicht immer, sondern eben nur manchmal bzw. ab und zu Primzahlen.

Damit aber zurück zu

"[...] gehen also mit einem einzigen Gegenbeispiel all unsere ach so schönen Vermutungen den Bach runter!"

Das ist aber wirklich bitter schade:

• nicht nur, dass wir mit dem soeben entdeckten Verfahren deshalb doch nicht beweisen können, dass es unendlich viele Primzahlen gibt;
• sondern das Verfahren wäre auch geeignet gewesen, etwa mit Hilfe eines Großrechners nacheinander massenhaft Primzahlen zu berechnen

(wenn auch - nochmals - nicht alle).

Mit solch einem nun leider gescheiterten Verfahren hätten wir einen uralten Mathematikertraum erfüllt: ein simples Verfahren, mit dem sich nacheinander massenhaft und potentiell alle Primzahlen berechnen lassen. Die Primzahlen wären nicht mehr so "individualistisch", sondern wir hätten endlich eine Regel für ihr Auftauchen gefunden.

Es sei kurz ergänzt, dass es den MathematikerInneN bis heute nicht gelungen ist, solch eine Regel zu finden. Und unten werden wir auch noch sehen, dass das trotz allem vielleicht auch gut so ist.

Und dennoch ist das Verfahren

r =                m                      + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● ...● p _n ) + 1

nicht gänzlich schlecht: mit ihm lassen sich immerhin doch immer mal wieder Primzahlen finden!

So langweilig es gewesen sein mag, oben die r für n = 2 , n = 3 , n = 4 , n = 5 und n = 6 zu berechnen; und so frustrierend es gewesen sein mag, dann wider Erwarten für n = 6 zu scheitern

(genauer: jeder normale Mensch hätte ja vermutlich nach Bestätigung der Vermutung für n = 2 und n = 3  aufgehört und [fälschlich] angenommen, dass das Verfahren in alle Ewigkeit so weitergeht, also verlässlich Primzahlen ergibt;

und ich hatte ja nur deshalb stur [und besserwisserisch] bis n = 6 weiter gemacht, weil ich ja geahnt hatte, dass das Verfahren irgendwann [und glücklicherweise nicht erst z.B. für n = 1000 ] nicht mehr funktionieren würde):

das Scheitern bei n = 6 und das Ergebnis 30031 = 59 ● 509 hatten eben doch ihr Gutes, denn daran wird deutlich, wie wir durch leichte Abwandlung der Vermutung vielleicht dennoch weiter kommen können.

Schauen wir uns daher den (gar nicht so) tragischen Fall n = 6 nochmals genauer an:

Vorausgesetzt war da, dass es nur n = 6 Primzahlen gibt, nämlich 2, 3, 5, 7, 11 und 13. Dann ergibt sich, wie gezeigt, r = 30031, was leider keine Primzahl mehr ist.

Interessant ist nun aber

(und damit machen wir sozusagen aus der Not eine Tugend),

warum r = 30031 keine Primzahl ist: eben weil es darstellbar ist als r = 30031 = 59 ● 509. Und das Wichtige daran ist:

r ist als Produkt der beiden Primzahlen 59 und 509 darstellbar, die beide größer als die bislang angenommene größte Primzahl p ₆ = 13 sind.

Das kommt so harmlos daher und ist doch ENORM WICHTIG:

auch hier zeigt sich: die Annahme, dass p ₆ = 13 die größte Primzahl ist, führt zur Entdeckung der beiden noch größeren Primzahlen 59 und 509, d.h. auch hier muss die anfängliche Annahme falsch gewesen sein.

(Hier sei nicht geklärt, weshalb bei der Annahme, dass es nur 6 Primzahlen gibt, dann doch - und zwar nicht zufällig, sondern mit eisernern Unerbittlichkeit - zwei größere Primzahlen herauskommen, sondern um diesen Aufsatz nicht noch länger werden zu lassen, als er notgedrungen sowieso schon ist, sei das unten am allgemeinen Fall gezeigt.)

Halten wir nochmals kurz inne, um uns klar zu machen, welche Vorteile, aber auch welche Grenzen Konkretisierungen haben:

1. kann man an konkreten Zahlen besser erste "Effekte" sehen, weil man mit ihnen noch eine Vorstellung verbinden kann;
2. lässt sich mit einigen wenigen konkreten Zahlen besser oder überhaupt erst rechnen;
3. kommt man wohl überhaupt erst mit einigen konkreten Beispielen auf Vermutungen über alle Fälle;
4. aber darf man dennoch nicht leichtfertig von einigen wenigen konkreten auf massenhaft oder gar unendlich viele Fälle schließen, sondern kann die Beschäftigung mit einigen wenigen Beispielen nur zu Vermutungen führen, die

• evtl. auch für viele oder gar alle zutreffen

(was zu beweisen wäre)

• oder sich aber (evtl. schon bei der nächstgrößeren Zahl) als falsch erweisen

(solch ein [einziges!] Gegenbeispiel bringt jede Vermutung zum Einsturz - oder erfordert zumindest eine Modifizierung der Vermutung).

Damit aber zurück zur allgemeinen Darstellung

r =                m                           + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● ...● p _n ) + 1   .

Die derart "zurechtkonstruierte" Zahl hat nun aber, wie wir schon anhand der Konkretisierungen erahnen konnten, bemerkenswerte Eigenschaften:

Wenn man sie durch irgendeine der Primzahlen p ₁, p ₂, p ₃ ...p _n dividiert, bleibt immer jeweils der Rest 1 über

(wir hatten ja durch Addition der 1 regelrecht dafür gesorgt).

Anders gesagt:

Halten wir nochmals inne, um die geniale Einfachheit der Konstruktion von

m =  p ₁ ● p ₂ ● p ₃ ● ...● p _n

und

r =                m                            + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● ...● p _n ) + 1  

staunend zu bewundern:

Nun ist aber doch, wie wir wissen, JEDE natürliche Zahl, also auch r, durch eine Primfaktorzerlegung darstellbar.

Was aber folgt aus diesem offensichtlichen Widerspruch?:

• erste Möglichkeit:

weil r ja nicht in andere Primfaktoren zerlegt werden kann, ist es wieder alles Erwarten SELBST eine Primzahl, und da r offensichtlich sehr viel größer als die (vermeintlich) größte Primzahl p _n ist, haben wir mit r eben DOCH eine noch größere Primzahl als p _n gefunden.

Nennen wir diese größere Primzahl probeweise mal p _n+1 .

Dann folgt:

p n war also DOCH NICHT die größte Primzahl!

• zweite Möglichkeit:

r ist (wie sehr viel eher zu erwarten) NICHT selbst eine Primzahl, müsste dann aber durch eine Primfaktorzerlegung mit ANDEREN Primzahlen als p ₁, p ₂, p ₃ ...p _n darstellbar sein.

(Denn wir hatten ja soeben gezeigt, dass r NICHT durch die Primfaktoren p ₁, p ₂, p ₃ ...p _n darstellbar ist.)

Hier aber erweist sich eine scheinbare Kleinigkeit von oben als eben doch sehr wichtig: wir hatten ja vorausgesetzt, dass wir mit der Reihe  p ₁, p ₂, p ₃ ...p _n bereits ausnahmslos alle Primzahlen, also auch keine versehentlich ausgelassen hatten.

Jetzt aber stellt sich heraus, dass es noch mindestens EINE WEITERE, GRÖSSERE Primzahl geben muss

(vgl. oben im Fall n = 6 die beiden Primzahlen 59 und 509).

Nennen wir diese größere Primzahl probeweise mal p _n+1 .

Auch hier folgt also:

p n war also DOCH NICHT die größte Primzahl!

Insgesamt haben wir also erhalten:

Nachbemerkungen:

Es gibt also - wie schon angedeutet - zwei ähnliche Beweiswege, wobei ersterer ein Ausschnitt des letzteren ist:

• erster Weg:
  • Annahme: es gibt nur endlich viele Primzahlen,
  • Widerspruchsbeweis , dass es mindestens eine zusätzliche Primzahl gibt,
  • Folgerung: es gibt doch unendlich viele Primzahlen,
  • Widerlegung der anfänglichen Annahme;
• zweiter Weg:
  • Annahme: es gibt unendlich viele Primzahlen;
  • Probeannahme des glatten Gegenteils, dass es eben doch nur endlich viele Primzahlen gibt;
  • Widerspruchsbeweis , dass es mindestens eine zusätzliche Primzahl gibt;
  • Widerlegung der Probeannahme,
  • Bestätigung der anfänglichen Annahme.

Bei diesem zweiten "Umweg" spricht man auch von einem "indirekten Beweis", der sich in der Mathematikgeschichte als ungemein ergiebig erwiesen hat, wenn man nicht auf direktem Weg zum Ziel kommt.

Dieser indirekte Beweis wirkt nun aber ein wenig "an den Haaren herbeigezogen", unredlich und vielleicht auch gehirnausrenkend.

Deshalb ein nichtmathematisches Beispiel:

Vorausgesetzt sei, dass der gesuchte Elefant hier im Raum ist. Und ich möchte nun beweisen, dass er im Kühlschrank ist, der nur leider abgeschlossen ist.

Ich nehme daher probeweise an, dass er außerhalb des Kühlschranks (aber doch hier im Raum) ist. Nach langer Suche stelle ich aber fest, dass er nicht außerhalb des Kühlschranks ist. Also bleibt nur, dass er im Kühlschrank ist.

Wir hatten oben schon betrauert, dass es uns mit

r =                m                      + 1 =

  = ( p ₁ ● p ₂ ● p ₃ ● ...● p _n ) + 1

leider (wider erstes Erwarten) nicht gelungen ist, ein einfaches Verfahren zu finden, mit dem man massenhaft Primzahlen erzeugen kann.

Und ich hatte auch schon ergänzt, dass die MathematikerInnen trotz intensiver Suche bis heute kein solches Verfahren gefunden haben.

Das hat doch immerhin den ersten Vorteil, dass die Primzahlen "individualistisch" bzw. rätselhaft bleiben

(wie ein Schüler mal sagte: es wäre schlimm, wenn man Atlantis finden würde, denn erstens könnte das bitter enttäuschend aussehen und zweitens gäbe es dann kein Ziel der Sehnsucht mehr).

Überhaupt haben die MathematikerInnen mit den Primzahlen nach wie vor allergrößte Schwierigkeiten:

1. können sie zwar schon sehr große Primzahlen bestimmen (vgl. ), aber das doch nur mit enormem Aufwand und keineswegs nach einer hübsch einfachen Formel.
2. haben sie (was unten noch sehr wichtig werden wird) ihre lieben Schwierigkeiten bei der Zerlegung größerer Zahlen in ihre Primfaktoren (vgl. ).

Hier wird es aber auch Zeit, mal darüber zu staunen, was wir oben geleistet haben: wir haben gezeigt, dass gewisse Zahlen in "größere" Primfaktoren als p _n zerlegbar sind, wenn wir auch oftmals nicht wissen, in welche. Sowas nennt man in der Mathematik einen (doch wahrhaft erstaunlichen!) "Existenzbeweis".

3. Immerhin sind die MathematikerInnen aber schon einer Sache näher gekommen, die wir oben auch schon ansatzweise betrieben hatten:

• wenn man schon nicht weiß, wo genau die einzelnen Primzahlen liegen,
• möchte man doch allzu gerne wissen, wo sie ungefähr liegen, ob sie also - obwohl es unendlich viele von ihnen gibt - immer seltener auftauchen (vgl. die berühmte "Riemannsche Vermutung").

Abschließend sei auf das zurückgekommen, was oben schon mehrfach angedeutet wurde: dass bei Primzahlen die Unendlichkeit tatsächlich ausnahmsweise mal eine Anwendung hat.

Primzahlen werden nämlich standardmäßig benutzt, um Botschaften (u.a. Bankdaten) zu verschlüsseln.

Wie genau das funktioniert, soll hier nicht erklärt werden (man vergleiche etwa   ).

Nur soviel: man nehme zwei riesige Primzahlen und multipliziere sie miteinander.

Dabei kann ein Computer sowohl das Auffinden dieser Primzahlen als auch das Ausmultiplizieren übernehmen.

Entscheidend ist, dass aber kein Computer der Welt die Chance hat, nachträglich (außer durch höchst unwahrscheinliche Zufallstreffer) halbwegs schnell herauszufinden, aus welchen beiden ursprünglichen Primzahlen das Ergebnis berechnet wurde.

Vgl. dazu nochmals die Quelle : da ist es erstmals gelungen, eine 158stellige Zahl in ihre Primfaktoren zu zerlegen. Aber so gewaltig sich 158 Stellen anhören, so lächerlich ist das doch im Vergleich mit der bislang größten bekannten Primzahl, die  9.808.358 Stellen hat (vgl. nochmals ). Und wie viele Stellen mag dann erstmal das Produkt zweier so gigantischer Primzahlen haben!

Verschlüsselungen mit Primzahlen funktionieren also nur deshalb so gut,

1. weil es unendlich viele Primzahlen, also (nachweislich) ein riesiges Reservoire von ihnen gibt,
2. weil man so wenig über Primzahlen weiß. Und deshalb ist es auch nur gut, dass wir oben mit unserem Versuch, eine einfache Formel für Primzahlen zu finden, gründlich gescheitert waren.

Aber mal angenommen, jemand würde doch zwei Formeln finden, mit denen man sehr einfach

• Primzahlen errechnen
• und große zusammengesetzte Zahlen in Primfaktoren zerlegen könnte

(immerhin gibt es da allerdings schon Abkürzungsverfahren!):

damit bräche von einem Tag auf den anderen alle derzeitige Geheimhaltungstechnik zusammen, was wohl eine wahre Katastrophe wäre.

Allerdings werden inzwischen bereits andere und dann vielleicht endgültig sichere Geheimhaltungsverfahren angedacht. Vgl. etwa:

"[...] [es] stehen [mit der Teleportation] neue, sichere Verschlüsselungsverfahren für Nachrichten zur Diskussion: Zuerst wird teleportiert, aber der Empfänger weiß nicht, was er erhalten hat. Danach bekommt er auf anderem Wege die Information, ob die Teleportation funktioniert hat [,] und kann nun das Ergebnis der Teleportation richtig bewerten, also die Information verstehen. Diesen Prozess kann ein Datenspion nicht nachvollziehen."
(zitiert nach , S. 57f;

hier sei nicht überlegt, ob totale Geheimhaltbarkeit überhaupt wünschenswert ist.)

Anhand der Primzahlen wird man vielleicht erahnen:

"Es heißt, der Erste Weltkrieg sei der Krieg der Chemiker gewesen, weil zum ersten Mal Senfgas und Chlor eingesetzt wurden, der Zweite Weltkrieg der Krieg der Physiker, weil die Atombombe abgeworfen wurde. Der Dritte Weltkrieg würde der Krieg der Mathematiker werden, weil die Mathematiker die nächste große Kriegswaffe, die Information, kontrollieren würden. Mathematiker haben die [Computer-]Codes entwickelt, die gegenwärtig militärische Informationen schützen. Es überrascht nicht, daß sie auch an vorderster Front im Kampf um die Entschlüsselung dieser Codes stehen."
(Simon Singh)

Viele PseudomathematikerInnen sind ja so scharf darauf, ihre Existenz durch Anwendbarkeit zu legitimieren. Singhs Satz zeigt aber, dass das gar nicht automatisch gut ist.

Umgekehrt kann man wohl aber auch nicht mehr so naiv sein, "reine" Mathematik ohne jede potentielle Anwendbarkeit zu betreiben, also sich "die Finger nicht schmutzig zu machen". Vgl. : G.H. Hardy: A Mathematicians Apology; Cambridge University Press.