Bruchrechnungsaufgaben auf dem Prüfstand

... "selbstregulierten" Lernens

Vorsicht, exzessives Nachdenken!

Vorbemerkungen
diskutierte Aufgaben
       erste Aufgabe
       zweite Aufgabe
       dritte Aufgabe(n)


Vorbemerkungen:

Bevor man immer nur sehr allgemein ach so wichtiges "selbstreguliertes" Lernen fordert bzw. sich

(um zu keiner Tat kommen zu müssen!?)

dabei irgendwann zu Tode differenziert (vgl. "was ist Selbstlernen"), werde man doch besser konkret:

1. entweder, indem man selbst Aufgaben dazu entwickelt (und sich der Diskussion darüber stellt),

2. oder, indem man sich fertige Aufgaben anderer Leute vornimmt

und sie dann 

(am besten im konkreten Unterricht, was hier allerdings leider nicht möglich ist)

auf den Prüfstand selbstregulierten Lernens stellt, also fragt:

halten diese Aufgaben, was sie versprechen, d.h.

• sind sie wirklich zum "selbstregulierten" Lernen geeignet?

• setzen sie dieses nicht nur voraus (was meistens schiefgeht), sondern fördern sie es auch gezielt?

Und wenn

• ja, was haben diese Aufgaben an sich, das sie für "selbstreguliertes" Lernen geeignet macht?

(... so dass das Prinzip ja eventuell auf andere Aufgaben übertragen werden kann, denn auf Dauer brauchen wir ja doch das eine oder andere Aufgaben"rezept" [wenn auch sicherlich nicht Patentrezept].)

• nein, wie ließen sich diese Aufgaben denn für "selbstreguliertes" Lernen geeignet machen?

(... falls nicht schon die Grundkonstruktion jegliche "Selbstregulation" zerstört.)

Ich möchte hier (feige?) den zweiten Weg gehen, mir also

• fertige Aufgaben

(oder zumindest erste Vorschläge)

• anderer Leute vornehmen.

Das mathematische Thema (der Anlass) ist fast beliebig,

Was ich hier also nicht treiben möchte, ist etwas durchaus Lehrertypisches: eine "Hinrichtung" der Aufgaben anderer

(und damit dieser anderen selbst!?),

ohne selbst Verbesserungsvorschläge zu machen.

(Und ich werde sowieso nie verstehen, wie man sich dazu hergeben bzw. es sich anmaßen kann, sozusagen hauptberuflich die Aufgaben anderer LehrerInnen zu kritisieren.)

Es gibt ja die zwei geradezu unversöhnlichen Extreme:

1. "eine Krähe kratzt der anderen kein Auge aus", d.h. man diskutiert nie ernsthaft, sondern nickt immer (auch zum letzten Müll) beifällig,

2. die Aufgaben anderer LehrerInnen sind immer Anlass zur Besserwisserei.

Dennoch wird man auch "kritisieren" dürfen, ohne Verbesserungsvorschläge zu machen. Vgl. etwa soziale Kritik oder Literaturkritik

(die ja nicht so schier unerträglich gouillotinenhaft wie bei Marcel Reich-Ranicki sein muss).

Im Hinblick auf die unten genannten Aufgaben kann ich nur sagen: im schlechtesten Falle sind es Standardaufgaben, wie auch ich (!) sie andauernd benutze.

Wie schon gesagt: das mathematische Thema (der Anlass) ist fast beliebig - und doch wurde hier mit gutem Grund die Bruchrechnung und damit ein Standardthema des Mathematikunterrichts gewählt:

1. ist es ja so einfach (?), sich methodische Alternativen bei inhaltlichen Exkursen auszudenken (vgl. etwa ?), aber das gerät doch leicht in den Verdacht, "nicht prüfungsrelevanter Luxus" zu sein, zu dem man außerdem unter dem Stoff- und Klausurdruck meist (angeblich?) gar keine Zeit hat.

2. Dass der "Selbstregulationsansatz" überhaupt funktioniert und eine Alternative im regulären Unterricht sein kann, ist nur anhand von Standardthemen überzeugend.

(... obwohl ich der festen Überzeugung bin: keine wirklich neuen [und sinnvollen!] Methoden ohne neue Inhalte!)

3. lohnt die Bruchrechnung gerade deshalb, weil sie so standardmäßig eingefahren ist: man ist da allzu leicht betriebsblind für Alternativen - und sollte gerade deshalb nach diesen Suchen suchen

(und "beweisen", dass es tatsächlich anders als üblich geht).

4. ist - zumindest meinem Eindruck nach - die Bruchrechnung (gerade wegen des massenhaften Rechnens) bei SchülerInneN derart unbeliebt, dass es sich da um so mehr lohnen würde, endlich "Selbstregulationsansätze" zu entwickeln.

5. stellt sich vielleicht gerade bei (Bruch-)Rechenverfahren die Frage, ob bzw. in welchen (eng gesteckten?) Grenzen da überhaupt "Selbstregulationsansätze" möglich sind (vgl. etwa   ). Es kann da nicht bei der Behauptung bleiben, dass das

• sehr wohl,

• zumindest ansatzweise (wann?)

• oder aber gar nicht geht,

sondern die Frage ist an Beispielen (und verschiedenen Unterrichtsphasen) zu überprüfen.

Noch kurz dreierlei:

1. Ich werde im Folgenden teilweise die Reflexionen dazuerfinden (müssen), die meine Aufgabenlieferanten vermutlich bei der Erstellung ihrer Werke angestellt, wie alle Künstler aber nicht explizit mitgeliefert haben. 

2. Ich zitiere die Aufgaben aus der (vermutlich ungenauen) Erinnerung und nehme mir sogar die Freiheit, sie auf gewisse methodisch relevante Punkte hin zuzuspitzen:

"Eine Ähnlichkeit mit den ursprünglichen Aufgabenlieferanten ist rein zufällig."

3. Ich bin mir durchaus bewusst, dass die im Folgenden betriebenen detailliertesten Text-, aber auch Grafikuntersuchungen (bis hin zur Problematisierung von Einzelwörtern) etwas Kleinkariertes bis geradezu Lieblos-Besserwisserisches an sich haben. 
   Aber das ist exemplarisch dennoch mal nötig, um ein Gespür für die vielen unscheinbaren, oftmals sogar ungewollten Implikationen von Aufgabenstellungen zu entwickeln. Im Berufsalltag hat dafür aber natürlich niemand Zeit, und ich will auch weiß Gott nicht jedes (vor allem mündlich formulierte) Wort auf die Goldwaage legen

(wie seinerzeit meine heißgeliebte Fachleiterin es tat).

Ich bin vielmehr sogar fest überzeugt, dass die Sprache im Unterricht auf keinen Fall immer absolut korrekt sein darf: vieles ist umgangssprachlich erheblich kürzer, leichter und anschaulicher darstellbar

(auch und gerade, um den Wirklichkeitsbezug zu bewahren),

und sowieso sollte man laut Martin Wagenschein die SchülerInnen vermehrt bei ihrer Sprache abholen.

diskutierte Aufgaben:

1. Aufgabe:

"Schneide einen [tatsächlich an die SchülerInnen verteilten!] einen Meter langen
  [Hart-]Plastikstreifen

1. in genau zwei gleich lange Stücke,

2. in genau vier gleich lange Stücke,

3. in genau acht gleich lange Stücke."

An dieser Aufgaben ist aber dennoch bis zu den Einzelwörtern hin alles diskutierenswert

(oder genauer: ich habe so lange an der Aufgabe "gedreht", bis das der Fall war).

"Diskutierenswert" heißt wahrhaft nicht "schlecht", sondern bedeutet "nur", dass je nach Kontext und Absicht verschiedene Varianten möglich sind.

Misslungen scheint mir nur eine einzige Kleinigkeit: gemeint ist wohl

• nicht     "genau zwei  gleich lange Stücke"  (statt z.B. 1 ¹/₂ oder 2 ¹/₄ Stücke),

• sondern "zwei genau gleich lange Stücke" (dass also die beiden Stücke gleich lang sein sollen).

Aber der Einwand ist absolut nebensächlich bis geradezu kleinkariert-besserwisserisch (Deutschlehrer!), da SchülerInnen den "falschen" Satz "genau zwei gleich lange Stücke" dennoch sicherlich richtig verstehen werden: niemand wird z.B. 1 ¹/₂ oder 2 ¹/₄ Stücke ausschneiden

(und zudem käme dann mit dem Rest zusammen eben doch wieder eine ganzzahlige Menge von [wenn auch verschieden langen] Stücken zusammen [3 bzw. 4 Stück]).

Als Ziele der Aufgabe wären etwa denkbar:

1. das (vermutliche) mathematische Ziel: die SchülerInnen sollen erkennen, dass ¹/₂, ¹/₄ und ¹/₈   durch mehrfaches Halbieren erreichbar sind.

Dabei ist die Aufgabenstellung durchaus "zwiespältig":

• einerseits wird da eben mit der Reihenfolge ¹/₂, ¹/₄, ¹/₈  schon die Grundstruktur vorgegeben,

(bei anderen Bruchfolgen würde das mehrfache Halbieren ja nicht funktionieren),

• andererseits bleibt (scheinbar) offen, dass mehrfach halbiert werden muss, denn nach  von Halbieren ist ja nie ausdrücklich die Rede

(aber bei der Anweisung "schneide" wird es dennoch impliziert mitgeliefert, denn z.B. ¹/₄ ist gar nicht mehr aus 1, sondern nur noch aus dem bereits abgeschnittenen ¹/₂ erhältlich).

Von diesem ersten Ziel aus ist auch eine genauere Verortung der Aufgabe in der Gesamtunterrichtseinheit möglich. Bzw. es gibt da verschiedene, durchaus jeweils sinnvolle "Verortungen":

• da  in der Aufgabe noch gar nicht die Bruchschreibweise und auch kaum (außer vielleicht alltägliche) Vorkenntnisse erwartet werden, könnte die Aufgabe durchaus "Opener" der gesamten Bruchrechnungseinheit sein;

• vielleicht will man aber vorweg ein gewisses Grundverständnis von Brüchen (Halbe, Drittel, Viertel ...) an anderen (noch einfacheren?) Aufgaben vermitteln und die vorliegende Aufgabe erst dann einsetzen, wenn es um die Beziehung zwischen verschiedenen Brüchen geht (¹/₄ ist die Hälfte von ¹/₂ ); Die vorliegende Aufgabe wäre also durchaus auch als "Gleichnamigkeits-Propädeutik" denkbar.

• mit "¹/₂ mal ¹/₂ gleich ¹/₄" wird aber auch schon die spätere Bruchmultiplikation geschrammt (s.u.).

Man muss halt wissen, was man will und

• die Aufgabe danach aussuchen,

• dementsprechend klären, welcher spezielle Aspekt von den SchülerInnen hinterher (evtl. an ein und derselben Aufgabe) "gekonnt" sein soll.

Neben dem ersten, rein mathematischen Ziel gibt es aber auch denkbare "pädagogische" Ziele:

2. Die SchülerInnen sollen anhand "handgreiflicher" Materialien (also nicht bloß auf Papier) und regelrecht "handwerklich" (also nicht bloß mit Bleistift oder gar im Kopf) allererste simple Aufteilungen vornehmen

(die zudem schon gestuft sind: die Unterteilung in zwei gleiche Teile kann sicherlich noch jedeR, aber auch die Unterteilung in vier und acht gleich lange Teile?).

3. Vielleicht ist es sogar ein (legitimes!) Ziel, den SchülerInneN erste Kontakte zur Bruchrechnung dadurch zu vereinfachen (schmackhaft zu machen), dass sie etwas tun, was sie sowieso schon können

(der [riskante, s. 4.] Beginn mit einem kalkulierten Erfolgserlebnis).

Somit lässt sich später an Bekanntem anknüpfen (Systematisierung, Erweiterung, Variation ...).

4. Ein weiteres (ebenfalls durchaus legitimes!) Ziel wäre es auch, überhaupt erst "abzuprüfen", ob die SchülerInnen (bzw. welche SchülerInnen) solch eine Aufgabe denn tatsächlich schon "von sich aus" erfüllen können.

(Erfahrene LehrerInnen wissen doch ganz genau, dass SchülerInnen oftmals nicht beherrschen, was eben die LehrerInnen für selbstverständlich hielten. Und das liegt nicht an der [zunehmenden?] Blödheit "der SchülerInnen von heute", sondern an ihrem entwicklungsgemäßen kognitiven, handwerklichen und verbalen Stand. Es ist beispielsweise für FünftklässlerInnen gar nicht so einfach, mit einem Geodreieck eine Gerade durch zwei gegebene Punkte zu zeichnen!

Wie aber in jedem Fall, in dem die SchülerInnen [erwartbar oder nicht erwartbar] etwas nicht können, wäre zu fragen, wie dann eine Hilfe aussehen könnte [s.u.].)

Die Aufgabe im obigen Wortlaut enthält aber anscheinend noch andere, verborgenere Ziele

(bzw. eventuell werden da Verläufe vorweggenommen und Ziele festbetoniert, die der Aufgabenerfinder sich nichtmal bewusst gemacht und vielleicht sogar gar nicht gewollt hat, die also kontraproduktiv sein können.
Wohlgemerkt: sowas passiert jedem von uns andauernd - und allemal, wenn man, nunmal Fachfrau/-mann, fast gar nicht mehr anders kann, als vom fertig systemisierten Endziel aus zu denken.)

Um diese verborgeneren Ziele zu erkennen, muss man sich aber den (von mir frisierten) Aufgabentext Wort für Wort anschauen

(denn hinter fast jedem Einzelwort steckte eine [und sei´s unbewusste oder versehentliche] Entscheidung bzw. Richtungsgebung).

Lassen wir uns dazu also die Einzelwörter mal sozusagen "auf der Zunge zergehen":

1. Warum schneide?

(... was natürlich mit der Wahl des Materials, also von Hartplastik, zusammenhängt)

2. Warum ein ein Meter langes Stück?

(... und nebenbei: warum wird das nochmals erwähnt, wenn die an die SchülerInnen verteilten Plastikstücke schon einen Meter lang sind?)

3. Warum aus [Hart-]Plastik?

4. Warum gleich lang (bzw. sogar genau gleich lang)

5. Warum 2, 4, 8 - und in dieser Reihenfolge?

Es wird keiner bestreiten können, dass dadurch eine enorme und von Wort zu Wort zunehmende Engführung stattfindet,

... die ja durchaus beabsichtigt und sinnvoll sein mag.

(Ob bzw. wie weit das aber zum "selbstregulierten" Lernen passt

[es ermöglicht, fördert, anleitet, abwürgt],

ist dabei allerdings eine ganz andere, später zu beantwortende Frage.)

Zu 1. und 3., also "schneide" sowie "[Hart-]Plastik":

(Nebenbei: an dem arg umständlichen Wort "Hartplastikstück" wird man vermutlich längst bemerkt haben, dass ich hier die ursprüngliche Aufgabenstellung am deutlichsten zu meinen "kritischen" Zwecken hingebogen habe.)

Manchmal fallen solche Entscheidungen ja ganz pragmatisch: es waren halt nur (Hart-)Plastikstücke zur Hand, oder sie waren besonders preiswert. Und diese (Hart-)Plastikstücke lassen sich nunmal nur - etwa mit einer kräftigen Schere - schneiden, weil sie beim Knicken zersplittern.

Merkwürdigerweise hängt die Entscheidung für "schneide/Plastik" aber schon mit "ein Meter" zusammen:

Zu 2., also "ein Meter":

Mit der Entscheidung zu dieser besonders einfachen Länge lenkt man die Tätigkeit der SchülerInnen unweigerlich in eine bestimmte Richtung

... und da ist es auch keine glaubwürdige "Ausrede", dass die Wahl mal wieder rein pragmatisch verlaufen sei: die Plastikstücke, die man noch im Keller hatte, waren alle zufällig genau einen Meter lang. Denn der zusätzliche explizite Hinweis auf die sowieso schon gegebene Länge hebt ja die besondere Länge hervor, es soll also nicht irgendein Plastikstück (egal welcher Länge) geteilt werden.

Und der explizite Hinweis auf die Länge macht es auch unglaubwürdig, dass man nur erreichen wollte (was ja durchaus sinnvoll wäre!), dass

• die SchülerInnen ihre Ergebnisse hinterher durch Messen oder Nebeneinanderlegen vergleichen können,

• man selbst die Ergebnisse der SchülerInnen leichter kontrollieren kann

(was natürlich nur funktioniert, wenn alle mit gleich langen Anfangsstücken beginnen).

Welche "bestimmte" Richtung wird denn nun aber - wie oben behauptet - durch die Längenangabe "ein Meter" nahegelegt?

Dazu überlege ich mal, wie ich das "Problem" lösen würde:

• wenn das (harte!) Plastikstück die einfache und zudem explizit genannte Länge ein Meter hätte, würde ich vermutlich die Hälfte (Viertel, Achtel) mit einem Lineal abmessen - und da dann schneiden (s. 1. und 3.),

• wenn das Ausgangsstück aber eine "krumme" Länge (z.B. 98,3 cm) bzw. eine mir unbekannte Länge hätte und zudem nicht (s. 3.) aus Hartplastik, sondern biegsam (z.B. aus Stoff oder Papier) wäre, würde ich erst gar nicht umständlich ein Lineal herbeischaffen und abmessen, sondern die Hälfte (Viertel, Achtel) durch Übereinanderlegen der beiden Enden und Knicken herausfinden - und dann erst (falls überhaupt noch nötig) schneiden bzw. reißen.

Nun ist aber - neben den oben genannten rein pragmatischen Gründen - sehr wohl ein methodisch-didaktisch sinnvoller Kontext für ein Abmessen (statt Knicken) denkbar: beispielsweise dann, wenn es nicht (in erster Linie) um Bruchrechnung, sondern um Prozentrechnung geht, bei der 1 m = 100 cm natürlich höchst hilfreich ist

(dann sieht man ja hinterher hübsch anschaulich [bzw. umgekehrt: braucht es bereits bei der Konstruktion], dass der Bruch ¹/₂ der Prozentangabe 50 entspricht.

Wenn die Aufgabe aber bei der Prozentrechnung eingesetzt würde, wäre es vielleicht sogar sinnvoll, fertige Papier-Zentimetermaße [wie sie in allen IKEA-Kaufhäusern rumhängen] zu verteilen, auf denen die Zentimeterangaben also schon aufgedruckt sind).

Eine Bedeutung des Abmessens für die reine Bruchrechnung sehe ich aber, ehrlich gesagt, nicht.

Anders gesagt: ich würde

1. ein einfacher zu beschaffendes und vermutlich auch preiswerteres Material, nämlich z.B. Papier oder Stoff, nehmen, das zudem ganz bewusst knickbar wäre,

2. zwar zwecks gegenseitiger und Lehrerkontrolle gleichlange Ausgangsstücke verteilen

(und in einer späteren Aufgabe zu verschieden langen Ausgangsstücken bei gleicher Arbeitsanweisung übergehen?),

3. ein "krummes" Maß (eben z.B. 98,3 cm) wählen und es nicht explizit nennen,

4. statt "schneide" offener "teile" sagen

(da haben die SchülerInnen die Wahl, wann sie die Aufgabe als erfüllt ansehen: schon beim Knicken oder erst beim Zerschneiden).

Um die endlosen Überlegungen scheinbar ad absurdum zu treiben: Ich würde sogar ein Papier- einem Stoffstreifen vorziehen, weil bei ersterem die Knicke besser sichtbar bleiben. Solche Materialeigenschaften sind dabei durchaus didaktisch wichtig:  nur wenn die Knicke sichtbar bleiben (und nebenbei nicht geschnitten wird), kann am Ende 

• auch wieder auseinandergefaltet,

• also der Lösungsweg nachträglich überschaut und wiederholt werden

• und bleibt auch jederzeit ein Vergleich des Teils mit dem Ganzen möglich.

Die Aufgabenstellung mit "ein Meter" und "schneide" (inkl. "[Hart-]Plastik") könnte noch den anderen (beabsichtigten oder zu vermeidenden) Effekt haben, dass damit sozusagen die Bruchrechnung in die Arithmetik verlegt bzw. auf diese zurückgeführt wird: die SchülerInnen halbieren (evtl. auch vierteln oder achteln) gar kein Material mehr, sondern die Längen, also (unter Abzug der Maßeinheiten) Zahlen

(und zwar den SchülerInnen wohlbekannte natürliche Zahlen!).

Zu 4., also "gleich lang" bzw. sogar "genau gleich lang":

1. Könnte es wünschenswert sein, dass die SchülerInnen (bei bewusst fehlender diesbezüglicher Aufgabenstellung) nicht gleich lange Stücke abschneiden?

(Anders gefragt: ist eigentlich für SchülerInnen so absolut selbstverständlich, was für LehrerInnen natürlich unabdingbar ist: dass bei Division durch eine Zahl gleichgroße Stücke zustande kommen? Rennt die Aufforderung "gleich lang" also nur offene Türen ein, könnte [sollte] man sie dann also weglassen?

Oder muss man die SchülerInnen vor völlig in die Irre führenden und sinnlosen Umwegen schützen, und zwar auch, damit sich nicht Falsches festsetzt oder dieses erst gar nicht entsteht? Denn jede Wette: viele Missverständnisse werden durch den Mathematikunterricht überhaupt erst erzeugt.)

2. Wieso legt der Aufgabensteller so großen Wert auf die Betonung "genau gleich lang". Reicht nicht auch "gleich lang", ist das also mit "gleich" nicht schon mitgesagt? Ist ohne "genau" allzu ungenaues Arbeiten erwartbar? Umgekehrt: Kann es sinnvoll sein, das "genau" wegzulassen und somit verschieden große Teile bewusst zu provozieren?

(Nebenbei: das sind für mich in a. und b. echte, nicht bloß rhetorische Fragen.)

Und wie genau hätte der Aufgabensteller es denn gern - und warum?

("Darf´s ein bisschen mehr sein?")

Reicht da das reine Augenmaß

(die Hälften sollen gleichlang aussehen),

und

• muss man dieses Augenmaß bei SchülerInnen voraussetzen, darf man sie also nicht für allzu "dumm" halten,

• oder muss man damit rechnen, dass zumindest einige von ihnen es noch nicht haben?

(... und könnte in letzterem Fall die [mit dem Schneiden implizierte] Anweisung, die Hälften abzumessen, hilfreich sein?)

• Oder will der Aufgabensteller nur der Schlamperei einiger einschlägig bekannter SchülerInnen vorbauen?

Zu überlegen wäre auch, ob die Anweisung "genau gleich lang" irgendeine Konsequenz hat:

• ist sie eine "selbsterfüllende Prophezeiung", d.h. werden die SchülerInnen dann allesamt automatisch etwa gleich lange Stücke erstellen?

• Oder ist erahnbar, dass einige SchülerInnen trotz dieser Anweisung völlig unterschiedliche "Hälften" erstellen - und was dann?

• wie merken die SchülerInnen das

(von selbst, durch ausdrücklich eingeforderten Vergleich der Hälften bzw. der eigenen Ergebnisse mit denen der MitschülerInnen, durch Lehrerkontrolle?),

• wie können sie sich dann selbst helfen bzw. welche Hilfe wird ihnen dann gegeben (s.u.)?

• Falls SchülerInnen es aber "nicht so genau nehmen": Woher soll die Motivation kommen, nachzubessern?

Hier hängt alles zusammen: 

• beim Schneiden können grobe Fehler passieren,

• beim Knicken wohl kaum.

Fragt sich also, ob man anders als in der ursprünglichen Aufgabe engführen, also nicht das Schneiden, sondern das Knicken "vorschreiben" sollte?

zu 5., also "2, 4, 8" und "in dieser Reihenfolge":

Die Begründungen hierfür sind sonnenklar: beabsichtigt sind wohl

1. sehr einfache Teilungen

(beispielsweise ¹/₃, also periodisches Teilen, ist [bei der Ausgangslänge 1m, nicht aber bei der Ausgangslänge 90 cm] schon [wenn man eben "genau" sein will] nicht mehr möglich).

2.  mehrfaches Halbieren nacheinander

(da scheint mir die Aufgabe - wie oben schon angedeutet - schon auf die Bruchmultiplikation zu zielen - was ja Absicht sein mag; ).

Und dennoch: ist die Engführung "2, 4, 8" sinnvoll? Wäre es also nicht durchaus wünschenswert, den sich andeutenden (und wichtigen!) Einheitsmechanismus mal auf schwierigere Aufgaben hin zu durchbrechen, also z.B. mittels ¹/₂, ¹/₄, ¹/₅?

¹/₅ ist aber nicht mehr durch Knicken erreichbar, und schon stellt sich die Frage, ob man dem durch die Anweisung "Abmessen/Schneiden" vorbeugen oder - gerade in einem "selbstregulierten" Unterricht - schweigen sollte.

Bei der Reihenfolge ¹/₂, ¹/₄, ¹/₅  kommt hinzu, dass die SchülerInnen (anders als bei ¹/₂, ¹/₄, ¹/₈ ) nicht mehr mit einem bereits zerschnittenen Streifen weiterarbeiten können, sondern einen neuen Streifen brauchen.

Mit der ursprünglichen Anweisung "schneide" in Kombination mit "¹/₂, ¹/₄, ¹/₈ " ist also impliziert, dass man die nächst kleineren Stücke aus den vorherigen herstellen kann. Ein anderer Weg ist nach Zerschneiden auch gar nicht mehr möglich. 

Fragt sich nur, ob man durch die Aufgabenstellung vorwegnehmen darf (muss), was doch eine selbst zu entdeckende Erkenntnis sein könnte.

So langsam müsste deutlicher überlegt werden, was oben nur mehrfach angedeutet wurde:

Wie sähen Hilfen aus, falls SchülerInnen die Aufgabe

(ist das überhaupt erwartbar?, bzw. evtl. wider Erwarten)

nicht bearbeiten könnten oder mittendrin stecken blieben?

(Implizit stellt sich natürlich dabei auch die Frage, welche Schülerprobleme überhaupt erwartbar bzw. erahnbar sind. Dabei kann einE erfahreneR LehrerIn sicherlich

• einige Probleme besser vorausahnen,

• bei nicht erahnten Problemen schneller und angemessener reagieren.)

Da aber würde ich dreiteilen, nämlich 

• erst überlegen, welche Hilfestellungen ich denn als Lehrer geben würde,

• dann aber weiterdenken, wie diese Hilfestellungen "selbstreguliert" (durch die Einzel- bzw. MitschülerInnen) erfolgen könnten

• und ich die SchülerInnen zu solcher "Selbstregulation" anleiten bzw. befähigen könnte/müsste (statt diese "Selbstregulationsfähigkeiten" - meist fälschlich - vorauszusetzen).

Ich nehme beispielhaft einen ersten "Fehler", der durch die Aufgabenstellung sogar fast - wenn auch sicherlich unbeabsichtigt - nahelegt wird

(Vieles scheitert allerdings auch an der bei gewissen SchülerInnen ja durchaus üblichen ungenauen Lektüre):

Einige SchülerInnen missverstehen die Logik der für sie ungewohnten, stichpunktartig eingerückten Aufgabenstruktur

aaa

• bbb

• ccc

• ddd .

Sie erkennen also nicht, dass in ccc wieder das Ganze (1) aus aaa zerlegt werden soll (jetzt in allerdings in vier Teile), sondern meinen, dass das Ergebnis aus bbb (¹/₂) gevierteilt werden müsse.

Dieser "Fehler" wird durch die Aufgabenstellung sogar noch anderweitig nahegelegt: wenn die SchülerInnen in bbb erstmal die eine Hälfte abgeschnitten und die andere achtlos weggelegt haben, dann aber in ccc die Vierteilung gefordert wird, wenden die SchülerInnen diese Arbeitsanweisung halt auf das einzige noch sichtbare Stück (also ¹/₂) an.

Nun hatte ich "Fehler" bewusst in Anführungszeichen geschrieben, denn zwar ist die gezeigte Vorgehensweise falsch im Hinblick auf den Aufgabentext, aber - und deshalb hatte ich gerade diesen "Fehler" gewählt - durchaus produktiv:

• entweder schaffen die SchülerInnen, die den vorliegenden "Fehler" machen, von sich aus die (schwierigere) Vier-Teilung,

• oder sie fangen halt von vorne mit einer Zweit-Teilung an.

Ein naheliegenderer "Fehler" könnte sein, dass jemand die Aufgabe zwar durchaus (richtig) versteht, aber nicht den Hintersinn der Reihenfolge, nämlich dass ccc aus bbb (und ddd aus ccc) folgt, indem man einfach nochmals halbiert.

Man könnte auch sagen: da ist die Aufgabe schon so hübsch suggestiv, nur bemerken einige SchülerInnen die Suggestivität leider nicht.

Die Suggestivität "rächt" sich aber doppelt, denn mir scheint, dass bei diesem "Fehler" auch nur eine überaus suggestive Hilfe möglich ist: "halbiere nochmals!"

Aber warum immer nur negativ, also über Fehler reden?: bei der Aufgabe "befürchte" ich mindestens ebenso sehr, dass einige SchülerInnen nach wenigen Sekunden fertig sind.

Dann müsste doch (zumindest in einem Stationenzirkel) sofort Aufgaben parat sein

(und auf sie hingewiesen werden!),

die für solche leistungsstärkeren SchülerInnen eine echte gestufte Herausforderung wären.

Bei der hier behandelten Aufgabe sind aber noch viel grundsätzlichere, sozusagen "außermathematische" Fragen möglich:

• "Wieso sollen die SchülerInnen überhaupt irgendwelche [völlig abstrakten bzw. rein innermathematisch sinnvollen] Streifen zerschneiden?"

• Gibt es also einen echten und glaubwürdigen, zumindest aber für SchülerInnen reizvolleren "Anwendungsaspekt", anhand dessen mathematisch Dasselbe (vorausgesetzt: innermathematisch Wünschenswerte) erreichbar wäre?

(Eine ganz andere Frage wäre allerdings, ob überhaupt immer ein Anwendungsbezug wünschenswert und sinnvoll ist: "Nicht immer, aber [zumindest doch] öfter!")

Ich bezweifle, dass es solche "Anwendungsaspekte" gibt, sondern sehe da nur zwei Möglichkeiten:

1. Man nimmt einen "Anwendungsaspekt" und passt ihm das mathematische Ziel an.

(Auf Anhieb fällt mir solch ein "Anwendungsaspekt" allerdings nicht ein!)

2. Oder man nimmt zumindest ein interessanteres Material, bei dem den SchülerInneN gleiches, d.h. gerechtes Teilen wünschenswert erscheint, also z.B. Kuchen.

(Da müsste man "gleich groß" vermutlich nichtmal erwähnen.
Fragt sich allerdings, ob der Aufwand, Kuchen zu backen, lohnt - und ob die SchülerInnen damit nicht doch nur "rumsauen" bzw. ihn einfach aufessen werden, bevor sie zu irgendeiner "Bruchrechnung" kommen.)

Ein guter Tipp scheint mir aber das oben benutzte Wort "reizvoll" zu sein: wenn schon keine sinnvollen Anwendungsaufgaben vorliegen (?), so sollten die Aufgaben doch einen "inneren" Reiz haben: ich also würde - zumindest dann, wenn "Selbstregulation" das Ziel wäre - die oben vorgestellte Aufgabe vollständig "in die Tonne hauen" und stattdessen z.B. folgende Aufgaben stellen:

1. Aufgabenalternative:

Ich würde versuchen, möglichst große rechteckige Blätter (Tapetenstücke?) aufzutreiben und die offene Aufgabe stellen:

"Knicke das Blatt so oft wie möglich!"

Und nebenbei: ich würde an verschiedene Schüler(gruppen) verschieden große Rechteckstücke verteilen

(natürlich mit dem Hintergedanken, dass kleinere Stücke weniger oft knickbar sind).

Wohlgemerkt: ich würde durch die offene Aufgabenstellung alle Arten von (z.B. auch schrägen oder auch Drittel-)Knicken zulassen, aber eben doch darauf vertrauen, dass zumindest einige SchülerInnen auf das Halbierungsverfahren kämen. Andere Lösungen (z.B. paralleles Falten [wodurch besonders viele Knicke möglich sind], aber sogar Zerknüllen) wären auch richtig - und sogar mathematisch produktiv, da vermutlich ungleiche Flächen entstünden.

Im Kern würde mit dieser Aufgabe dasselbe erreicht wie mit der oben genannten, aber man wird bemerkt haben, dass in der neuen Aufgabe keinerlei (direkte) mathematische Anweisungen enthalten sind.

Der behauptete "innere Reiz" der Aufgabe wäre dabei ein dreifacher:

1. ein noch rein handwerklicher (also nicht bereits erkennbar mathematischer) Wettbewerb in der Klasse

(wer schafft - auch durch ordentliches Arbeiten - die meisten Knicke? Wobei allerdings natürlich diejenigen benachteiligt wären, die kleinere Anfangsstücke bekommen hätten - und also zu fragen wäre, ob nicht doch alle mit gleichgroßen Stücken anfangen sollten);

2. stellt sich vermutlich irgendwann automatisch die Frage, wie oft selbst bei einem sehr großen Ausgangsstück geknickt werden kann;

(vgl. dazu:

"Frage: Wie oft kann man ein beliebig großes Papier in der Mitte höchstens falten?

Kurzerläuterung: Man kann jedes Blatt Papier höchstens sieben- bis achtmal falten (je nach Dicke des Papiers).

Wissenschaftliche Erläuterung:

Wenn man ein Papier immer weiter in der Mitte faltet ist das in der Tat nur sieben- bis achtmal möglich. Denn bei jedem Falten verdoppelt sich die Anzahl der Blätter, die geknickt werden müssen.

1. Mal: 1 Blatt
2. Mal: 2 Blätter
3. Mal: 4 Blätter
4. Mal: 8 Blätter
5. Mal: 16 Blätter
6. Mal: 32 Blätter
7. Mal: 64 Blätter

Beim 9. Mal müssten also 256 Blätter gefaltet werden. Das ist nicht möglich, da der Kraftaufwand auch für einen starken Menschen viel zu groß wäre. [...] Der Anstieg der zu faltenden Blätter erfolgt exponential: Wenn man es schaffen würde, ein Blatt 50mal zu falten, würde die Dicke des Stapels von der Erde bis zur Sonne reichen."
[zitiert nach ]

Ein weiteres Falten scheint mir allerdings auch dadurch unmöglich zu werden, dass sich innen so merkwürdige, zunehmende Papierquetschungen ergeben:

 )

3. scheint mir der "infinitesimale" Prozess bei dieser Aufgabe viel deutlicher zu sein: beispielsweise ¹/₁₆ und ¹/₃₂ werden selbst dann noch von den SchülerInnen gedacht werden, wenn sie technisch schon nicht mehr möglich sind.

Vor allem aber werden ¹/₂, ¹/₄, ¹/₈ ... weitgehend selbst entdeckt, ohne dass jemals ausdrücklich von ihnen die Rede war.

(Um ehrlich zu sein: was in der ursprünglichen Aufgabe ausdrücklich vorgegeben war, müsste bei der hier vorliegenden Aufgabe nachträglich herausdestilliert werden, und da stellt sich dann doch die Frage, ob das nicht auch wieder nur mit sehr suggestiven Mitteln möglich bzw. wie das vermeidbar wäre.)

2. Aufgabenalternative:

"Wir richten ein wahres Gemetzel an - und halbieren (wiederholt) alles und jedes, also verschiedene Materialien und verschiedene Größen."

(Auch hier spare ich mir [feige?] die weitere methodisch-didaktische Ausführung auf ein mathematisches Ziel hin.)

2. Aufgabe:

Während oben von einer einzigen Aufgabe die Rede war, soll hier an einigen Beispielen überlegt werden, welche Rolle Computerprogramme beim "selbstregulierten" Lernen spielen können.

Dazu sei zuerst ein Computerprogramm gedacht, das in zwei Modulen Folgendes "kann":

1. wenn man in das erste Modul einen "abstrakten" Bruch (z.B. ³/₄ ) eingibt, zeigt es eine entsprechende "Kuchen"-Teilung (also z.B. );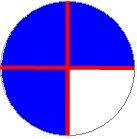

2. das zweite Modul verfährt genau umgekehrt: der Computer zeigt zufallsbedingt eine "Kuchen"-Teilung an, zu der man den entsprechenden Bruch eingeben muss - eine Eingabe, die dann auf Richtigkeit hin kontrolliert wird ("drill & kill").

Beide Module unterscheiden sich im Hinblick auf "selbstreguliertes" Lernen enorm:

• die Funktionsweise des zweiten Moduls ist genauso

(wodurch das Modul ja noch nicht schlecht ist)

durch ein Buch erreichbar, in dem massenhaft "Kuchen"-Teilungen abgedruckt sind, zu denen man die korrekten Brüche beispielsweise im Anhang nachschlagen kann.

Einzige Vorteile des Moduls gegenüber Büchern:

• ein kleines Computerprogramm (Modul) kann ganze Stapel von Büchern ersetzen,

• die Überprüfung, ob das eingegebene Bruch-Ergebnis richtig ist, ist viel umstandsloser und schneller möglich.

(Dabei sei hier mal davon abgesehen

[und schon gar nicht seien die Ursachen genauer untersucht],

dass Computer[programme] oftmals selbst dann auf SchülerInnen attraktiver wirken, wenn sie keinen Surplus gegenüber Büchern bieten.)

• das erste Modul hingegen ist überhaupt nicht in Papierform möglich, weil nicht vorweg zu ahnen ist (vorweggenommen werden soll), welche Brüche die SchülerInnen eingeben.

In diesem Sinne ist das erste Modul schon erheblich "selbstregulierter" als das zweite. Dennoch hat auch das erste Modul einen Nachteil: es ist allzu suggestiv, da es - falls richtig programmiert - immer alles richtig macht.

(Es sei hier eingestanden, dass ich bei einem solchen Programm zu allererst ausprobiert habe, wo seine Grenzen sind, also beispielsweise mittels Brüchen, die größer als 1 sind, also z.B. ⁹/₇.)

Fragt sich nur, was an der tatsächlich freien Wahl von Brüchen (im ersten Modul) "selbstreguliert" sein soll. Man könnte ja auch böse sein und sagen:

"Jetzt endlich haben die SchülerInnen die freie Wahl, und zwar zwischen Coca oder Cola bzw. Krebs oder Cholera."

Denkbar wäre des weiteren ein Programm-Modul, das

• nicht die ewig gleichen Kreise, sondern andere zu "teilende" Gegenstände zeigen würde, also beispielsweise (zu füllende) Messbecher,

• oder sogar ein und denselben Bruch in verschiedensten "Grundeinheiten" ([verschiedene] "Kuchen" und [verschiedene] Messbecher und und und).

Der Vorteil solch eines Programm-Moduls läge "auf der Hand": sein Einsatz wäre mit erheblich weniger (überhaupt lohnendem?) materiellem und Zeit-Aufwand (und potentiell Dreck) verbunden als der von echten Kuchen, Messbechern ...

Dennoch sehe ich - gerade im Hinblick auf "selbstreguliertes" Lernen - einen entscheidenden Nachteil des Programm-Moduls, und zwar dann, wenn es

(was im Eifer des Unterrichtsgefechts ja geradezu Standard ist)

völlig die Kuchen, Messbecher usw. ersetzt: den SchülerInneN werden die "sinnlichen" Erlebnis geraubt:

• das (genaue!) Schneiden,

• das Zusammenschütten,

• das Überlaufen

• ...

Weiter angedacht sei ein Programm-Modul, das Bruchteile addieren kann, und zwar, indem es Messbecher simuliert und Flüssigkeiten zusammenschüttet. Man gibt also beispielsweise ein, dass ein erster Messbecher zu ¹/₂ und ein zweiter zu ²/₃ gefüllt sein soll. Als Ergebnis zeigt das Programm-Modul dann 1 ¹/₃ gefüllte Messbecher an.

Bemerkenswert (aber damit ja nicht schlecht) daran scheint mir, dass da Anschauung ohne Anwendung vorliegt (vgl. "Anschauung statt Anwendung"):

• Wann denn jemals schüttet man überhaupt im Alltag etwas zusammen?

(... außer vielleicht beim Zubereiten von Mahlzeiten nach Rezept, aber da kommen [zumindest in moderneren Rezepten] keine Bruch-, sondern nur Gramm- und Milliliterangaben vor, und zudem "schwappt" ein Gefäß nicht über, wenn man halbwegs Augenmaß bewahrt.)

• Wann denn jemals schüttet man Bruchteile zusammen?

Das einzige Beispiel, das mir einfällt, ist

Zweitaktgemisch

Kraftstoff/Schmieröl-Mischung (Verhältnis ca. 20:1 bis ca. 100:1). Zum Betrieb von Zweitaktmotoren (Motorrad, Moped).

Und selbst da ist nicht von Brüchen, sondern von Verhältnissen die Rede, was praktisch zudem bedeutet: ich schütte auf einen Liter Benzin 20 ml Öl (ganze Zahlen).

3. Aufgabe(n):

Hier im dritten Teil soll  es überhaupt nicht mehr um Einzelaufgaben, sondern um eine Folge von Aufgaben gehen

(und dann ab und zu doch wieder um das Aussehen von Einzelaufgaben).

Es gibt gute Gründe dafür, die SchülerInnen "häppchenweise", nämlich streng der Fachsystematik folgend, an die Bruchrechnung heranzuführen:

• so streng voneinander abgezirkelt, ist es sicherlich am einfachsten für die SchülerInnen,

• jeglicher Verwirrung und Vermischung von Problemen wird vorgebeugt, indem sie einzeln nacheinander vorgeführt werden,

• insbesondere können SchülerInnen nicht an komplexere und damit für sie evtl. noch gar nicht lösbare Aufgaben geraten

(... was hier durchaus erstmal als Vorteil gemeint ist).

Ein Beispiel: es werden nacheinander durchgenommen

(wobei vorausgesetzt sei, dass die SchülerInnen schon erweitern und kürzen können):

1. Themensegment: Addition gleichnamiger Brüche,

2. Themensegment: Addition ungleichnamiger Brüche,

"Selbstreguliert" sein kann dann durchaus

• das Bearbeitungstempo,

• die Auswahl aus verschiedenen Aufgaben aus demselben "Themensegment",

• die Auswahl verschiedener Veranschaulichungen zu demselben "Themensegment".

Zweifelsohne hat die gezeigte "kleinschritt-vorsortierte" Vorgehensweise aber auch Nachteile:

1. erschließen die SchülerInnen sich nicht die Probleme selbst

(trenne also nicht selbst die gleichnamigen von den ungleichnamigen Brüchen),

2. weiß es doch jedeR LehrerIn: sobald die Aufgaben nicht mehr so schön voneinander abgetrennt sind, sondern komplexer werden (Mehreres auf einmal "gefordert" wird), strecken viele SchülerInnen "alle viere von sich" und sehen "vor lauter Bäumen den Wald nicht mehr".

Da kann man sich nun streiten, wie damit umzugehen ist:

• Sollte man eben nach dem 1. (Addition gleichnamiger Brüche) und 2. Themensegment (Addition ungleichnamiger Brüche) ein drittes mit dem Arbeitstitel "Komplexeres" (also beispielsweise Addition sowohl gleichnamiger als auch ungleichnamiger Brüche) einbauen

(was wohl der übliche Weg ist; und nach diesem verlässlichen Prinzip funktionieren in Deutschland ja sogar die meisten Mathearbeiten:

• 1a) - f): zunehmend schwierigere Aufgaben zur Addition gleichnamiger Brüche,

• 2a) - g): zunehmend schwierigere Aufgaben zur Addition ungleichnamiger Brüche,

• 3a) - e): zunehmend schwierigere Aufgaben sowohl zur Addition gleichnamiger wie auch zur Addition ungleichnamiger Brüche [oder beides auf einmal]. Und spätestens in 3e) steht dann ein aberwitziges Gewusel aus mindestens zehn Brüchen.)

• Oder darf/muss man den SchülerInneN von Anfang an größere Komplexität zumuten - mit ihnen aber auch Wege erarbeiten, sich in dieser Komplexität zurecht zu finden?

Ein Kollege sagte mal auf einer Fortbildung, es sei die falsche Alternative, immer vorauszusetzen, dass die SchülerInnen etwas nicht könnten. Vielmehr müsse man sie so behandeln, "als ob" sie es durchaus schon könnten (vgl.: 16jährige verhalten sich oft noch sehr kindlich und haben dennoch das "verdammte" Recht, als Erwachsene ernst genommen zu werden). Sonst nämlich würden sie sich (und das scheint mir üblich zu sein) als prinzipiell dumm verkauft fühlen - und blocken: "Wie wir den Laden hier kennen, wissen Sie es schon, wir aber nicht. Also machen Sie es uns bittschön vor." Anders gesagt: wir haben die SchülerInnen ja regelrecht dazu erzogen, nur noch Kleinschrittiges zu wollen und jede komplexeren Aufgabe zu verweigern.

Warum sollte man den SchülerInnen sich im Gewusel der gleichnamigen und ungleichnamigen Brüche erstmal selbst zurechtfinden lassen?

Noch kurz erwähnt seien zwei andere Fälle, in denen üblicherweise unnötig vorstrukturiert wird:

1. in sämtlichen Darstellungen von Brüchen sind die Bruchteile immer gleich groß,

2. die Unterteilungen sind meist eingezeichnet, also 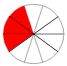  statt 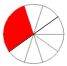   bzw. sogar ,

3. anfangs liegen zu addierende Bruchteile immer direkt nebeneinander oder zumindest so, dass sie einander nicht überlappen: also z.B.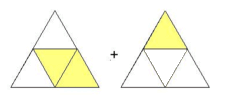statt ,

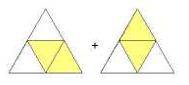4. zu addierende Bruchteile sind meist gleich orientiert, also z.B. statt .

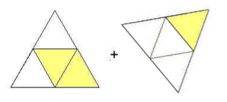5. ein Beispiel zur Addition ungleichnamiger Brüche, und zwar im vorliegenden Fall von ¹/₃ und ²/₅ .

Ein Arbeitsblatt dazu sieht dann z.B. folgendermaßen aus:

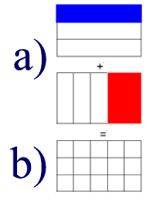
Das ist natürlich genial, also genial einfach. Aber es ist auch vollständig suggestiv. Ich hätte doch bei unverändertem a) nicht auch noch in b) die Quadrate vorweggenommen. Mein Verbesserungs(?)vorschalg wäre also

Für all diese Aufgabentypen gibt es allerbeste Gründe - und doch "kauen" sie alles vor, verhindern also alle eigenen Erkenntnisse von SchülerInnen bzw. unterstellen, dass sie diese sowieso nicht haben werden.