der Riemannsche Kreis

Bernhard Riemann
(1826-1866)

"coole und vor allem seeeehr anschauliche+einfache erklärung der riemannschen zahlenkugel, merci!!!" ( R.)

Riemann war ein allzu großes Genie und sein "Kreis" ist eine allzu genial einfache Sache, als dass ich sie mir hier auf meinen Seiten entgehen lassen könnte.

Ganz früh lernt man in der Schule den

Zahlenstrahl

kennen, um die Verhältnisse von Zahlen zueinander zu durchschauen bzw. sie anschaulich anordnen zu können:

im Laufe der Schuljahre werden da immer mehr Zahlen "drauf gepackt"

• erst auf die positive rechte Hälfte nur die natürlichen Zahlen (1; 2; 3 ...), immer hübsch im Abstand 1 und dazwischen Vakuum;

• dann zusätzlich auch auf die negative linke Hälfte die negativen ganzen Zahlen (-1; -2; -3 ...), insgesamt aber alle noch immer im Abstand 1 und nach wie vor dazwischen Vakuum;

• dann zusätzlich die rationalen Zahlen, also Brüche: so langsam füllt sich das bisherige Vakuum, die Zahlen liegen unendlich nah beieinander - und man sollte doch meinen, dass der Zahlenstrahl damit komplett ausgefällt sei;

• welch gehirnausrenkende Tatsache, ja welches Gefühl, reingelegt worden zu sein, wenn dann noch die irrationalen (unvernünftigen!) Zahlen hinzukommen
  (vgl. ).
  Erst jetzt mit allen bekannten, den sogenannten reellen Zahlen - so ließe sich zeigen (was aber im Schulunterricht nie geschieht - ist der Zahlenstrahl wirklich pickepacke voll, erst jetzt kann man alle Zahlen mit einem durchgehenden Strich einzeichnen.
  Gerade deshalb sollte man nun aber denken, dass damit auch schon alle nur irgendwie möglichen bzw. existenten Zahlen entdeckt seien, und genau da bleibt der meiste Schulunterricht ja auch tatsächlich stehen.
  (Es sei nur nebenbei erwähnt, dass sich die irrationalen Zahlen nochmals in die algebraischen und die transzendenten Zahlen unterteilen; vgl.   )

• Da hat es etwas Hinterhältiges bzw. Spitzfindiges, wenn nun doch noch zusätzliche Zahlen neben dem Zahlenstrahl, also in einer

Zahlenebene

eingeführt werden, nämlich die imaginären bzw. komplexen Zahlen (und einer der Rädelsführer war da Riemann!).

(Mit derselben Spitzfindigkeit könnte man Zahlen auch in einem 3-, 4- oder n-dimensionalen Raum anordnen.)

Nicht umsonst heißen diese Zahlen

• imaginär: unwirklich
• komplex, verwickelt, verflochten, verzweigt, zusammengesetzt, beziehungsreich; zusammenhängen (mit)
  (Duden),

und anfangs haben sich ja durchaus auch namhafte Mathematiker gegen "solch eine sinnlose Willkür" gewehrt.

Hier kann und soll nicht näher erklärt werden, weshalb man diese Zahlen in der Zahlenebene eingeführt hat und welche durchaus praktischen Anwendungen damit möglich sind

(die MathematikerInnen haben nachträglich selbst gestaunt, dass ihre Kopfgeburt anwendbar war).

Und es kann auch nur angedeutet werden, dass sich in dieser Zahlenebene höchst interessante Rechenmöglichkeiten durch Summierung von Pfeilen und Drehung ergeben.

Auf jeden Fall aber - und darum soll's hier gehen - hat die Zahlenebene einen entscheidenden Nachteil:

sehr "große" Zahlen liegen weit "draußen", und überhaupt geht die Ebene in jeder Richtung unendlich weiter.

Das lässt sich vielleicht noch halbwegs vorstellen (es gibt Zahlen kurz vor Moskau und in der Nähe des Jupiter), aber prinzipiell nicht zeichnen.

Und genau da hat Riemann eine genial einfache Idee gehabt, nämlich die

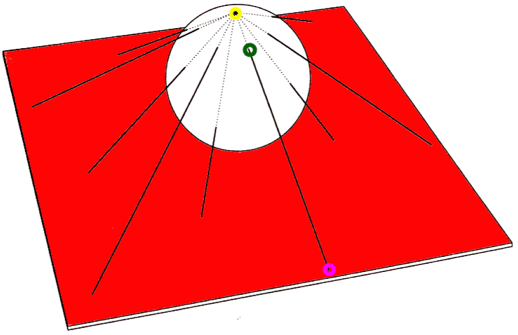
Riemannsche Zahlenkugel:

auf der Zahlenebene liegt eine Kugel auf, und nun wird jede Zahl in der Zahlenebene durch eine Strecke mit dem "Nordpol" dieser Kugel verbunden: der Punkt, an dem diese Strecke die Kugel durchstößt, ist dann das Abbild (sozusagen die Schusswunde) der Zahl auf der Zahlenkugel.

Der Vorteil dieser Kugel ist aber eben, dass sie "kompakt" (begrenzt) ist und nicht mehr (wie noch die Zahlenebene) in alle Richtungen unendlich "ausufert": man kann sie sozusagen in der Tasche mit nach Hause nehmen (und in der Tat sollten SchülerInnen ja was mit "nach Hause" nehmen können):

"He's got the whole [Zahlen-]world in his hand."

(Nebenbei: die Abbilder der Zahlen aus der Zahlenebene rutschen auf der Kugel immer weiter nach oben auf den "Nordpol" zu und unendlich nah an ihn heran, je weiter die Zahlen in der Zahlenebene außen liegen, also ins Unendliche "abwandern".)

Spätestens jetzt werden sich Laien aber fragen (und Fachleute haben's sicherlich schon beim Titel getan), weshalb ich dann in der überschrift vom "Riemannschen Kreis" statt von "Riemannscher Kugel" gesprochen habe.

Weil ich in mehr oder minder freier Assoziation die Zahlenkugel als Metapher für etwas (fast) ganz anderes benutze:

• es sei die "Zahlenebene" die (unendlich ausufernde) Menge aller mathematischen Erkenntnisse;

• am "Südpol" der Zahlenkugel bzw. ihrem Berührpunkt mit der Zahlenebene liegt ein anderer "Unendlichkeitspunkt": die graue Vorzeit, aus der keinerlei gesicherte Fakten bekannt sind
  (wer hat als erster den "Satz des Pythagoras" angewandt - und haben die Babylonier ihn vielleicht doch schon [vor Pythagoras] bewiesen???);

• in der Nähe des Berührpunkts in der "Zahlenebene" (bzw. ganz unten auf der "Zahlenkugel") liegen die einfachsten und ältesten bekannten mathematischen Tatsachen
  (also beispielsweise der "Satz des Thales");

• weiter außen in der "Zahlenebene" (bzw. höher auf "Zahlenkugel") werden die mathematischen Tatsachen immer schwieriger und (was hier der Einfachheit halber mal gleichgesetzt sei) moderner;

• ganz weit außen in der "Zahlenebene" (bzw. ganz oben auf der "Zahlenkugel") liegen also die neuesten mathematischen Erkenntnisse unserer Gegenwart
  (z.B. Andres Wiles' Beweis der "letzten Vermutung" von Fermat);

• und mit der unendlichen Weite der "Zahlenebene" (bzw. dem "Nordpol" der "Zahlenkugel") wird unterstellt, dass viele Erkenntnisse noch in der Zukunft liegen - und dass man nie ans Ende der mathematischen Erkenntnisse gelangen wird.

Was von dieser "Erkenntniskugel" lernen nun aber SchülerInnen kennen?

Ich unterstelle mal:

• weil's oben doch allzu schwierig wird, niemals die obere Hälfte
  (mathematische Erkenntnisse bis so etwa ins 18. Jahrhundert hinein - und aus der Zeit danach nur noch die Systematisierungen des Altbekannten);

• umgekehrt aber auch: weil Mathematik oftmals zu "abgehoben" statt anschaulich unterrichtet wird, auch nicht die untere Hälfte;

• insgesamt also nur den Kugeläquator, also einen (gar nicht so) Riemannschen Kreis!

Ich möchte damit unterstellen:

• man sollte viel anschaulicher, also vermehrt auf der unteren Kugelhälfte arbeiten
  (die ja immerhin die Gesamtkugel trägt),

• aber ebenso - und zwar immer mal wieder! - zumindest Perspektiven auf die obere Hälfte andeuten.

Es geht eben beispielsweise nicht an (und deshalb die ganze obige Zahlengeschichte), dass SchülerInnen im Irrglauben belassen werden, mit den reellen Zahlen seien auch schon alle bekannten Zahlen erledigt, und dass sie somit nie die imaginären und komplexen  Zahlen, also auch nicht die Riemannsche Zahlenkugel kennenlernen (an denen doch jeder zumindest mal "geschnüffelt" haben sollte - u.a. damit er weiß, was er später [nicht] studiert).

(Vgl. auch )

Zudem zeigt die obere Hälfte der mathematischen "Erkenntniskugel" Perspektiven für die angeblich ach so vielen Hochbegabten, denen da unendlich viel Stoff für freie Exkurse geliefert werden kann. Im üblichen Unterreicht bekommen sie ja meist nur schwierigere, nicht neue Aufgaben.

(Nebenbei: einE LehrerIn sollte zukunftsweisende Perspektiven der Mathematik immerhin dem Namen und der ganz knappen, vereinfachten Bedeutung nach kennen

[dazu müsste es eigene übersichtsbücher für LehrerInnen geben!],

aber sie/er muss sie wahrhaft nicht vollständig beherrschen, was bei der Komplexität der modernen Mathematik auch völlig ausgeschlossen ist:
der Professor des berühmten Weierstraß hat diesem [mit dessen Zustimmung] in der Examensprüfung eine bis dahin [auch von diesem Professor!] ungelöste Aufgabe gestellt, und selbst wenn Weierstraß keine Lösung gefunden hätte [oder es gar keine gäbe], hätte da dennoch abgeprüft werden können, ob der Kandidat "was" konnte.
Prüfungen [oder z.B. auch Facharbeiten] müssen nämlich nicht immer Fertiges, sondern können auch [unbeendete] Denkwege bzw. Herangehensweisen abprüfen.)