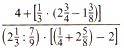Heiner Stauff - anschauliche Mathematik

der Röntgenblick

"Drei Blinde beschreiben einen Elefanten. Obwohl sie noch nie einen Elefanten in seiner ganzen Größe haben sehen können (sie sind seit Geburt blind), fühlen sie sich doch berufen, ein fachmännisches Urteil über einen Elefanten abzugeben. Denn alle drei hatten schon die Möglichkeit, in der Nähe eines Elefanten zu sein und ihn zu berühren und zu betasten.
Der erste, der nur den Rüssel untersucht hat, ist ganz sicher, dass der Elefant sich so ähnlich wie eine Schlange verhält. Der Zweite, der die lappigen, großen Ohren untersucht hat, weiß genau, dass der Elefant so ähnlich wie ein hängender Teppich ist. Und der Dritte, der ein Elefantenbein umklammert hat, findet an diesem Bein eine große Ähnlichkeit mit einer Säule, die er auch schon einmal umklammert hat.
So ist sich jeder seiner Meinung ganz sicher und total überrascht, dass die anderen, blinden Kollegen zu ganz anderen Meinungen kommen konnten. Es kommt zum Streit, weil keiner die Meinung der anderen akzeptieren kann, weil er doch mit seinen eigenen Händen den Elefanten erforschen konnte."
(zitiert nach )

Alle Berufe haben ihre bestimmte Brennweite, in der sie nur klar sehen können, bzw. ein ganz eigenes Raster , das sie über die Wirklichkeit legen:

Der Jurist interessiert sich oft (und zwar auch in privaten Diskussionen) nur für die existierenden Gesetze (egal, welche!), und was mit ihnen nicht erfassbar ist, geht für ihn über den Horizont hinaus und ist ein "weiches" Ziel, d.h. letztlich Blabla.
Der Jäger sieht im Wald nur Tiere, der Holzfachmann erkennt in den Bäumen nur Festmeter, und dem Dichter wird im "Deutschen Wald" ganz blümerant ums Herz.
Als ich mal mit einem befreundeten Orthopäden hinter einer langbeinigen Frau auf hohen Stöckelschuhen herging, sah er nur sich andeutende Fußprobleme.

Solches Spezialistentum bzw. - was dasselbe ist - solche Fachidiotie hat Vor- und Nachteile:

das komplexe und blutvolle Leben wird schrecklich reduziert, ja abgenagt

(eben zu einer Röntgenaufnahme: Knochen ohne Fleisch)

und meist nur noch monokausal bzw. zumindest nach wenigen Kriterien erklärt

(vgl. etwa die "Rasterfahndung", bei der einige wenige Suchkriterien für Kriminelle aufgestellt werden),

man erkennt aber gewisse Spezialaspekte und auch Zusammenhänge viel besser.

Der "Röntgenblick" reduziert massiv die Wirklichkeit, und ich habe mich immer gefragt, was eigentlich am Beruf des Röntgenarztes (Radiologen) so interessant sein sollte - außer dass man da angeblich besonders viel Geld verdienen kann.

Auch MathematikerInnen haben einen speziellen "Röntgenblick", indem sie hinter allen Phänomenen vor allem Zahlen und geometrische Figuren sehen.

Zwei Beispiele, wie MathematikerInnen sehen:

und noch rein innermathematisch:

Gegeben sei die Funktion f: y = -36x + 4x³

Bevor der Mathematiker damit irgendwas tut oder gar blind losrechnet

(und nebenbei: er hat sein Standardrepertoire, was da zu tun ist, nämlich z.B. eine Nullstellenberechnung [s.u.]),

wirft er sozusagen seine Texterkennungs-Scanner-Software bzw. seinen Parser an

(unter einem "Parser" versteht man ein Computerprogramm, das mathematische Ausdrücke in ihre Einzelteile, also z.B. Summanden, zerlegen kann).

Zu allererst "scannt" das Mathematikerauge nun den Funktionsterm -36x + 4x³ im Hinblick darauf, ob irgendwelche kompliziertere Sonderfunktionen, also z.B. "sin(us)", vorliegen.

Das ist nicht der Fall, und dementsprechend fällt unserem Mathematiker der erste Stein vom Herzen.

Zweiter Schritt: so unscheinbar (oft kleiner geschrieben) sie sind, so zentral wichtig sind sie doch: die Exponenten, also im Funktionsterm -36x + 3x³ die 3 oben am letzten x.

Diese Exponenten sagen unserem Mathematiker

(und zwar insbesondere, wenn er zwischenzeitlich noch im Geiste den Exponenten 1 ergänzt:

-36x¹ + 4x³ )

nun gleich zweierlei:

alle x stehen unten in der sogenannten "Basis" - und in den Exponenten oben nur Zahlen:

unserem Mathematiker fällt der zweite Stein vom Herzen.

Es liegt also keine Exponentialfunktion vor, bei der die x oben und die Zahlen unten stehen (z.B. 1^x und 3^x):

mit diesen Exponentialfunktionen wäre vollständig anders zu verfahren

und sie sind erheblich schwieriger zu behandeln;

letztlich interessiert unseren Mathematiker an -36x + 4x³ überhaupt nur der größte Exponent, also 3:

ausgerechnet das Kleinste am gesamten Ausdruck ist das Wichtigste:

Damit hat unser Mathematiker das entscheidend Wichtige gefunden - und der dritte Stein fällt ihm vom Herzen.

Jetzt weiß unser Mathematiker ziemlich genau, wie der Funktionsgraph der Funktion f: y = -36x + 4x³ aussieht und wie die Funktion sich im Prinzip verhält:

der Funktionsgraph von f: y = -36x + 4x³ ist s-förmig und sieht - abgesehen von Kleinigkeiten - so aus:

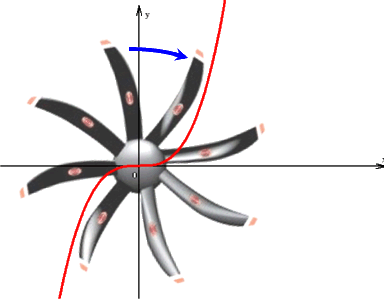
Alles andere an dem Funktionsterm, also

-36x

und die 4 vor x³ wird daran relativ wenig ändern

(nämlich nur noch strecken, verschieben und kleine "Beulen" einbauen)

und deshalb stellt unser Mathematiker die Summanden um und das Wichtigste nach vorne:

4x³ - 36x

Im Grunde interessieren sich MathematikerInnen sowieso

kaum für Einzelfunktionen,

sondern für ganze Funktionsklassen bzw. Funktionenscharen, also im vorliegenden Fall für alle Funktionen mit dem höchsten Exponenten 3, egal, welche Zahl davor steht (im vorliegenden Fall die 4).

Einige dieser Funktionsgraphen sehen so aus - aber sie sind alle s-förmig:

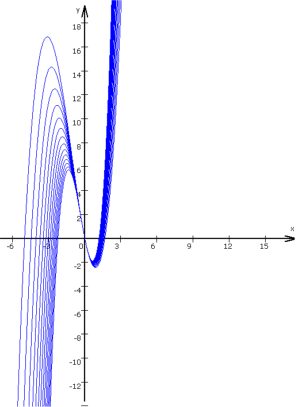
Weil unser Mathematiker schon die Grundform des Graphen kennt, nämlich die s-Form

(der Graph kommt von unten und geht nach oben - oder umgekehrt),

weiß er auch schon, dass mindestens eine Nullstelle vorliegt, weil der Graph dann

(da er stetig ist, also in einem durchgezogenen Strich ohne Lücken verläuft)

mindestens einmal die x-Achse durchstoßen muss.

(und wenn unser Mathematiker ein bisschen mehr Ahnung hat, weiß er auch schon, dass auch zwei oder höchstens drei Nullstellen vorliegen können).

Wenn nun Standardwerte wie eben die Nullstellen gesucht sind

(um zu bestimmen, wo der Funktionsgraph durch die x-Achse geht, und ihn also genauer lokalisieren zu können);

wenn nun also gefragt ist, wann (für welche[s] x)

4x³ - 36x = 0

gilt,

so schaut unser Mathematiker als Nächstes mit einem schnellen Blick, ob ganz hinten am Funktionsterm ein sogenanntes "absolutes Glied" (in dem kein x vorkommt) auftaucht, also z.B.

4x³ - 36x + 7 = 0

Bei 4x³ - 36x ist das nicht der Fall - und schon fällt unserem Mathematiker der vierte Stein vom Herzen.

Ohne dieses absolute Glied wird nämlich die Berechnung der Nullstelle(n) erheblich einfacher:

       4x³ - 36x                  = 0

(4x² - 36) • x             = 0

(4x² - 36) = 0 oder x = 0       N₁ ( 0 | 0 )

       4x² - 36 = 0   | : 4

    x² -   9 = 0   | + 9

    x² -   9 = 0   | + 9

    x²         = 9   | √

    x          = 3 oder x = - 3      N₂ ( 3 | 0 ) , N₃ ( -3 | 0 )

Insgesamt hat unser Mathematiker also ein wohlgeordnetes Zoom-Verfahren

(vgl. auch )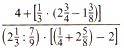

angewandt:

in den Exponenten stehen nur Zahlen (egal, welche),

der höchste und die Form des Graphen weitgehend bestimmende Exponent ist 3,

ganz am Ende fehlt das absolute Glied.

(das den Graphen sowieso nur vertikal verschieben würde).

Im Hinblick auf das Folgende sei schon darauf verwiesen, dass MathematikerInnen sich natürlich auch immer für das interessieren, was nicht vorhanden ist (oben eben das absolute Glied).

Seht ihr den Mond dort stehen
Er ist nur halb zu sehen
Und ist doch rund und schön
So sind wohl manche Sachen
Die wir getrost verlachen
Weil unsere Augen sie nicht seh'n
(Matthias Claudius)

Wenn unser Mathematiker beispielsweise die

Cheops-Pyramide

sieht, so

mag er als Privatmann über ihre enormen Ausmaße oder die enorme Bauleistung staunen

und gerade deshalb ihre Höhe herausfinden wollen

(wie seinerzeit schon

Thales
624? - 547? v. Chr.)

Und dazu "röngt" er die Pyramide, d.h. schaut in sie hinein:

er denkt (!) sich den Querschnitt

(den es derart ja gar nicht gibt bzw. wozu er die Pyramide eigentlich durchsägen müsste),

und darin wiederum die Höhe(nstrecke)

(die es auch nicht gibt bzw. wozu er die Pyramide eigentlich durchbohren müsste):

D.h. er macht zur Vereinfachung

aus etwas Dreidimensionalem (der Pyramide)

erst etwas Zweidimensionales (den Querschnitt)

und dann etwas Eindimensionales (die Höhe).

So dumm sind Mathematiker - und damit enorm erfolgreich.